算法训练营Day28
#Java #贪心
开源学习资料
Feeling and experiences:
这周来到了贪心算法,简要概述:
贪心算法是一种在每个步骤中都采取最优解(即,在当前看来最好的解)的算法设计策略。它通常用于求解优化问题。这种方法不总是能得到全局最优解,但在很多情况下能产生接近最优的解决方案。
这里是一些贪心算法的关键特点和应用实例:
1. 局部最优选择:在每个决策点,算法选择当前情况下的最佳选项,而不考虑未来的结果。
2. 无回溯:一旦做出选择,算法就不会撤销或重新考虑这个决策。
3. 应用领域:贪心算法适用于任务调度、图算法(如最小生成树和最短路径问题)、压缩编码(如霍夫曼编码)等。
4. 效率和简单性:通常,贪心算法比其他更复杂的算法更快、更简单。
5. 局限性:不是所有问题都可以用贪心算法有效解决。在某些情况下,贪心选择可能阻止达到全局最优解。
6. 实例:一个典型的例子是找零问题,即用最少的硬币数量找零。在美国货币系统中,使用贪心策略(总是选择可能的最大面值硬币)可以得到最优解。
要有效地应用贪心算法,关键是正确识别问题是否适合使用这种策略,并理解它可能只提供近似解而不是最优解。
分发饼干:力扣题目链接
假设你是一位很棒的家长,想要给你的孩子们一些小饼干。但是,每个孩子最多只能给一块饼干。
对每个孩子 i,都有一个胃口值 g[i],这是能让孩子们满足胃口的饼干的最小尺寸;并且每块饼干 j,都有一个尺寸 s[j] 。如果 s[j] >= g[i],我们可以将这个饼干 j 分配给孩子 i ,这个孩子会得到满足。你的目标是尽可能满足越多数量的孩子,并输出这个最大数值。
如果没有想到贪心的思想,正常解答也很容易解出来:
class Solution {public int findContentChildren(int[] g, int[] s) {//贪心,先满足胃口最大的孩子//先排序Arrays.sort(g);Arrays.sort(s); //都是从小到大升序排列int endg = g.length -1;int ends = s.length -1;int count = 0;while(ends>=0 && endg>=0){if(s[ends] >= g[endg]){count++;ends--;endg--;}else{endg--;}}return count;}
}官解用的是for循环,我认为while循环更容易理解
思路都是一样的,只要就是把这两个数组进行排序,这样我们从最后开始遍历比较,以我们的饼干数组为准。
从最大的满足度和饼干大小开始,逐一向下遍历。用两个指针endg和ends分别指向g数组和s数组的末尾元素(最大值)。
如果当前最大的饼干ends可以满足当前最大的满足度endg(即s[ends] >= g[endg]),则意味着这个孩子可以被满足。此时,将计数器count增加1,并将两个指针都向前移动一位,以检查下一个孩子和饼干。
如果当前饼干不能满足当前孩子(即s[ends] < g[endg]),则只将endg指针向前移动一位,检查下一个较小的满足度,因为当前饼干无论如何都无法满足当前孩子。
摆动序列:力扣题目链接
如果连续数字之间的差严格地在正数和负数之间交替,则数字序列称为 摆动序列 。第一个差(如果存在的话)可能是正数或负数。仅有一个元素或者含两个不等元素的序列也视作摆动序列。
-
例如,
[1, 7, 4, 9, 2, 5]是一个 摆动序列 ,因为差值(6, -3, 5, -7, 3)是正负交替出现的。 - 相反,
[1, 4, 7, 2, 5]和[1, 7, 4, 5, 5]不是摆动序列,第一个序列是因为它的前两个差值都是正数,第二个序列是因为它的最后一个差值为零。
子序列 可以通过从原始序列中删除一些(也可以不删除)元素来获得,剩下的元素保持其原始顺序。
给你一个整数数组 nums ,返回 nums 中作为 摆动序列 的 最长子序列的长度 。
class Solution {public int wiggleMaxLength(int[] nums) {if (nums == null || nums.length == 0) {return 0;}if (nums.length == 1) {return 1;}int maxCount = 1;Integer prevDiff = null; // 使用Integer以便能存储nullfor (int i = 1; i < nums.length; i++) {int diff = nums[i] - nums[i - 1];if (diff != 0) {// 只在差值符号变化时增加maxCountif (prevDiff == null || (diff > 0 && prevDiff < 0) || (diff < 0 && prevDiff > 0)) {maxCount++;prevDiff = diff;}}}return maxCount;}
}
最开始的一个想法是,把nums遍历计算,把得到的差放到另一个数组或者集合中,再用该数组或者集合进行遍历求解。
最大子序和:力扣题目链接
给你一个整数数组 nums ,请你找出一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。
子数组 是数组中的一个连续部分。
这道题利用前缀和来计算,非常简单:
class Solution {public int maxSubArray(int[] nums) {//初始化为数组的第一个元素int maxSum = nums[0];int sum = 0;for(int i = 0;i<nums.length;i++){sum += nums[i];sum = Math.max(sum,nums[i]);maxSum = Math.max(maxSum,sum);}return maxSum;}
}力扣评论:
走完这一生 如果我和你在一起会变得更好,那我们就在一起,否则我就丢下你。 我回顾我最光辉的时刻就是和不同人在一起,变得更好的最长连续时刻~~
Fighting!
相关文章:

算法训练营Day28
#Java #贪心 开源学习资料 Feeling and experiences: 这周来到了贪心算法,简要概述: 贪心算法是一种在每个步骤中都采取最优解(即,在当前看来最好的解)的算法设计策略。它通常用于求解优化问题。这种方…...

鸿蒙OS应用开发之日期选择
前面学习了时间选择组件,实现了时间的选择,这样非常方便用户进行时间的输入,通过手动就可以输入时间,比直接文本输入要省不少时间,特别对于手机这样单手操作的设备,更加重要了。因此,日期的输入工作也不能落后,本文将要学习日期选择组件,这样就可以实现日期通过手上下…...

Mysql 查看表注释或字段注释
查看所有表的注释 SELECT table_name 表名, table_comment 表说明 FROM information_schema.TABLES WHERE table_schema ‘数据库名’ ORDER BY table_name 查询所有表及字段的注释 SELECT a.table_name 表名, a.table_comment 表说明, b.COLUMN_NAME 字段名, b.column_commen…...

MySQL InnoDB引擎
1、逻辑存储结构 2、架构 a. 内存结构 Change Buffer的意义是什么? 与聚集索引不同,二级索引通常是非唯一的,并且以相对随机的顺序插入二级索引。同样,删除和更新可能会影响索引树中不相邻的二级索引页,如果每一次都操作磁盘&am…...
C++完成Query执行sql语句的接口封装和测试
1、在LXMysql.h 创建Query执行函数 //封装 执行sql语句 if sqllen 0 strlen获取字符长度bool Query(const char*sql,unsigned long sqllen0); 2、在LXMysql.cpp编写函数 bool LXMysql::Query(const char* sql, unsigned long sqllen){if (!mysql)//如果mysql没有初始化好{c…...

C:宏:编程风格:井号与define之间的空格
在这一篇中有提到,井号与define之间空格,可能导致搜索上的一些问题。 https://mzhan017.blog.csdn.net/article/details/135289451 今天看到有专门做这个空格的修改: https://sourceware.org/git/?pglibc.git;acommitdiff;hfcf70d4114db9ff…...
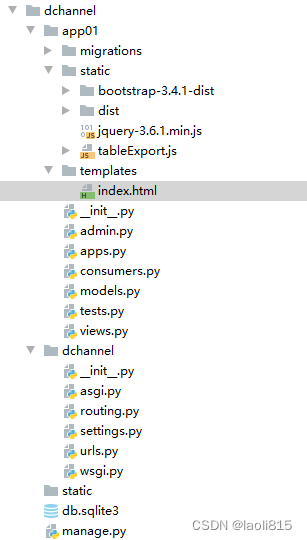
django websocket
目录 核心代码 consumers.py from channels.generic.websocket import WebsocketConsumer from channels.exceptions import StopConsumer import datetime import time from asgiref.sync import async_to_sync class ChatConsumer(WebsocketConsumer):def websocket_conne…...
HackTheBox - Medium - Linux - Bagel
Bagel 今天我开始了《Red Team Development and Operations A Practical Guide》的学习,保持学习,后面差不多到时机后就学CRTOⅡ Bagel 是一款中等难度的 Linux 机器,其特点是电子商店容易受到路径遍历攻击,通过该攻击可以获取应…...
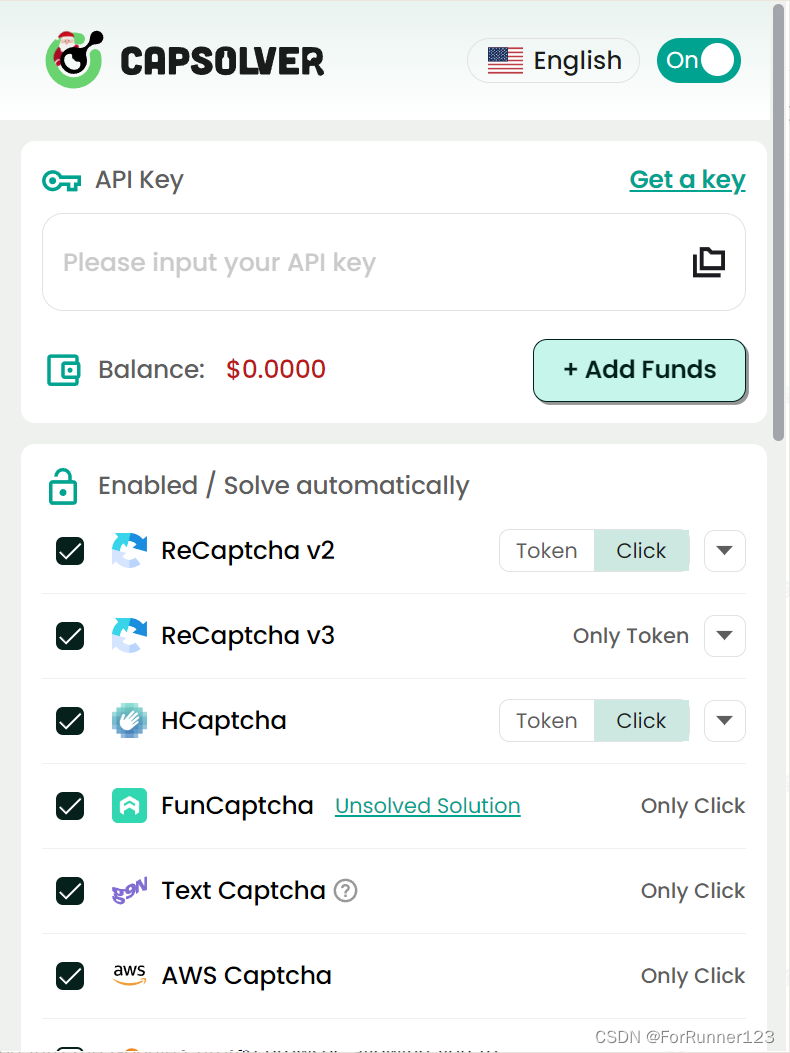
Capsolver:解决Web爬虫中CAPTCHA挑战的最优解决方案
Web爬虫已经成为从各种在线来源提取和分析数据的不可或缺的技术。然而,在Web爬取过程中,经常会遇到的一个共同挑战是CAPTCHA。CAPTCHA(完全自动化的公共图灵测试,用于区分计算机和人类)是一种安全措施,旨在…...

大数据系列之:读取parquet文件统计数据量
大数据系列之:读取parquet文件统计数据量 一、Spark读取parquet文件统计数据量二、parquet-tools统计parquet文件数据量三、实际应用案例 一、Spark读取parquet文件统计数据量 首先,创建一个 SparkSession 对象: val spark SparkSession.b…...

力扣题:字符串变换-1.5
力扣题-1.5 [力扣刷题攻略] Re:从零开始的力扣刷题生活 力扣题1:482. 密钥格式化 解题思想:首先先将破折号去除,并将所有字母转换为大写,然后计算第一组的长度,进行结果字符串的拼接,如果第一组的长度为0,则需要删除开头的’-符号 class S…...
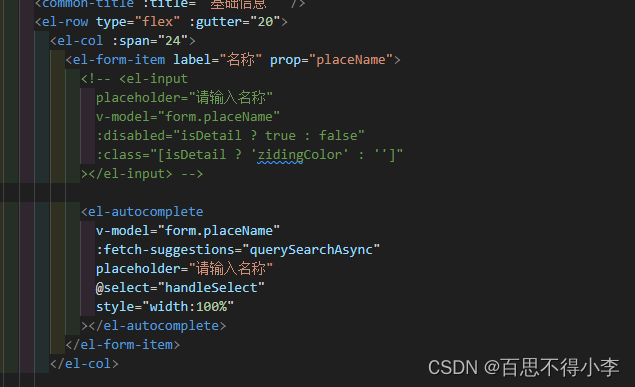
el-autocomplete远程搜索使用及el-upload上传多个文件流给后端,详情接口返回的是文件地址,前端将文件地址转成文件流,回传文件流给后端
最近遇到一个项目,里面有2个需求我觉得挺常见的,第一个需求是一个表单里,当用户在输入名称后,前端调接口发请求获取到关联名称的企业名称,并展示,然后当用户选中企业后,前端调接口获取选中企业的具体信息,并填充到表单里;第二个需求是,表单里有个上传图片的功能,前端…...

2024年度 ROTS - 实时操作系统 Top 15
RTOS(实时操作系统)。 这里说的 RTOS 并非新星球大战电影中的机器人,而是物联网设备、航空系统、空中交通管制等背后的无声协调者,就在地球上。 RTOS,或称实时操作系统,设计它们是为了更好的管理资源&…...
苹果怎么同步备忘录?教程来了,干货满满!
在苹果设备中,备忘录是一款非常实用的应用程序,可用于记录日常生活中的各种事项。然而,还有一些小伙伴不知道苹果怎么同步备忘录,这可能会成为他们的一个困扰。别着急!本文将详细介绍同步苹果手机备忘录的方法…...
 性能调优之 - 哪些层面可以进行优化)
Nginx(十八) 性能调优之 - 哪些层面可以进行优化
Nginx三大优势,动静分离、反向代理、负载均衡 1、线程 worker 2、http/tcp tcp_nopush tcp_nodelay 3、Buffer 调整请求体缓存区大小、将请求体缓存到一个缓冲区,降低CPU负载 4、连接队列 5、超时时间 6、静态文件缓存 open_file_cache 7、gzip压…...
neutron)
OpenStack云计算(三)neutron
neutron 介绍: Neutron 概述传统的网络管理方式很大程度上依赖于管理员手工配置和维护各种网络硬件设备;而云环境下的网络已经变得非常复杂,特别是在多户场景里,用户随时都可能需要创建、修改和删除网络,网络的连通性和隔离不已经太可能通过手工配置来保证了。 如…...
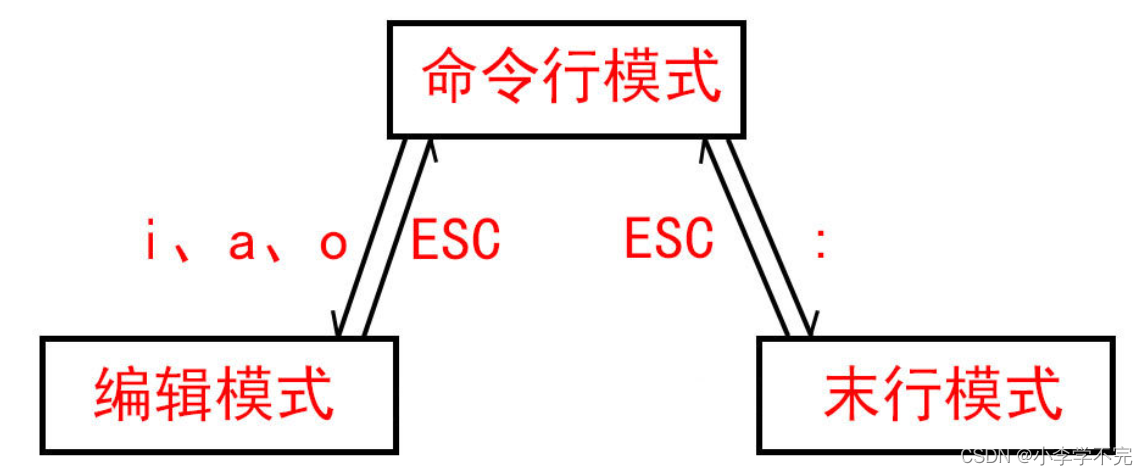
Linux期末复习笔记
一、管理文件系统 1、文件系统类型 ext2:早期Linux中常用的文件类型。ext3:ext2的升级版,带日志功能。RAMFS:内存文件系统,速度很快。NFS:网络文件系统,由SUM发明,主要用于远程文件…...

PHP实现多继承
php支持多继承吗 不可以,只支持单继承。 可以使用 interface 或 trait 实现 。 实现方法 https://www.php.cn/faq/430197.html https://blog.58heshihu.com/index.php/archives/2288/...

pulsar原来是这样操作topic的
本篇主要讲述pulsar topic部分,主要从设计以及源码的视角进行讲述。在pulsar中,一个Topic的新建、扩容以及删除操作都是由Broker来处理的,而Topic相关的数据是存储在zookeeper上的。本篇文章模拟一个高效的学习流程进行展开 介绍使用方式(To…...

日常工作 经验总结
1,在使用vue2开发项目时,快捷有效的组件化component 若有参数传递时,可以通过这样传递 在component中: 2,上拉加载,下拉刷新 若是使用局部进行上拉加载 下拉刷新 且需要用到scroll-view时 那么需要切记scroll-view在内被mescroll-uni包裹。若场景有限 对于无数据显示…...

Lombok 的 @Data 注解失效,未生成 getter/setter 方法引发的HTTP 406 错误
HTTP 状态码 406 (Not Acceptable) 和 500 (Internal Server Error) 是两类完全不同的错误,它们的含义、原因和解决方法都有显著区别。以下是详细对比: 1. HTTP 406 (Not Acceptable) 含义: 客户端请求的内容类型与服务器支持的内容类型不匹…...

【OSG学习笔记】Day 18: 碰撞检测与物理交互
物理引擎(Physics Engine) 物理引擎 是一种通过计算机模拟物理规律(如力学、碰撞、重力、流体动力学等)的软件工具或库。 它的核心目标是在虚拟环境中逼真地模拟物体的运动和交互,广泛应用于 游戏开发、动画制作、虚…...

系统设计 --- MongoDB亿级数据查询优化策略
系统设计 --- MongoDB亿级数据查询分表策略 背景Solution --- 分表 背景 使用audit log实现Audi Trail功能 Audit Trail范围: 六个月数据量: 每秒5-7条audi log,共计7千万 – 1亿条数据需要实现全文检索按照时间倒序因为license问题,不能使用ELK只能使用…...

抖音增长新引擎:品融电商,一站式全案代运营领跑者
抖音增长新引擎:品融电商,一站式全案代运营领跑者 在抖音这个日活超7亿的流量汪洋中,品牌如何破浪前行?自建团队成本高、效果难控;碎片化运营又难成合力——这正是许多企业面临的增长困局。品融电商以「抖音全案代运营…...

A2A JS SDK 完整教程:快速入门指南
目录 什么是 A2A JS SDK?A2A JS 安装与设置A2A JS 核心概念创建你的第一个 A2A JS 代理A2A JS 服务端开发A2A JS 客户端使用A2A JS 高级特性A2A JS 最佳实践A2A JS 故障排除 什么是 A2A JS SDK? A2A JS SDK 是一个专为 JavaScript/TypeScript 开发者设计的强大库ÿ…...

海云安高敏捷信创白盒SCAP入选《中国网络安全细分领域产品名录》
近日,嘶吼安全产业研究院发布《中国网络安全细分领域产品名录》,海云安高敏捷信创白盒(SCAP)成功入选软件供应链安全领域产品名录。 在数字化转型加速的今天,网络安全已成为企业生存与发展的核心基石,为了解…...

ThreadLocal 源码
ThreadLocal 源码 此类提供线程局部变量。这些变量不同于它们的普通对应物,因为每个访问一个线程局部变量的线程(通过其 get 或 set 方法)都有自己独立初始化的变量副本。ThreadLocal 实例通常是类中的私有静态字段,这些类希望将…...
)
ArcPy扩展模块的使用(3)
管理工程项目 arcpy.mp模块允许用户管理布局、地图、报表、文件夹连接、视图等工程项目。例如,可以更新、修复或替换图层数据源,修改图层的符号系统,甚至自动在线执行共享要托管在组织中的工程项。 以下代码展示了如何更新图层的数据源&…...

向量几何的二元性:叉乘模长与内积投影的深层联系
在数学与物理的空间世界中,向量运算构成了理解几何结构的基石。叉乘(外积)与点积(内积)作为向量代数的两大支柱,表面上呈现出截然不同的几何意义与代数形式,却在深层次上揭示了向量间相互作用的…...

ubuntu中安装conda的后遗症
缘由: 在编译rk3588的sdk时,遇到编译buildroot失败,提示如下: 提示缺失expect,但是实测相关工具是在的,如下显示: 然后查找借助各个ai工具,重新安装相关的工具,依然无解。 解决&am…...
