关于一名资深Java程序员在移动端的进阶之路
今天呢,就借此机会,跟大家聊一聊我的个人职业经历吧!
那年刚毕业
刚毕业时候,入职的第一家公司,进去后,说实话,没有太大成长吧!基本就是让我做一些可有可无的边缘性的工作,而且也从来没人催我赶进度。平时,也就帮人跑跑腿,取个快递或者帮人递送个开票文件。总之,说白了,就是一个打杂的小伙。
当时,给我安排的工作也是一些 web 页面很简单的一些内容。后来也是我身边那个哥问我,你有确定自己未来的方向吗?我说我想做后端,然后就跟着他做一些简单的 CRUD 工作,这也就算我入门后端了,当时我们后端是 Java 语言。从此我就开始了我的 Java 职业旅程。
初识移动端
H5开始入门
首先,我自己是主要做后端 Java 开发,但是业内应该都知道,Java 很卷的,起初,我做过 Jsp 页面的,后来是前后端分离,页面就是 Html ,还有移动端 H5 开发。
有了这些基础之后,当时,我们正好要做一个移动端 H5 的一套页面,而且时间也比较紧急,我就被安排跟我们一个前端大佬,一起做页面。跟着她,让我认识到了 HbuilderX 这个开发工具。
之前我用的是 VsCode 写页面,这也算是发现新大陆了。主要对于我这种不专业的前端开发人员来说,是一个非常不错的开发神器了。它的特点就是:入门超级简单。
微信小程序开发
这里我不得不说这个开发工具真心非常好用,等到做微信小程序的时候,我已经可以完全独立开发了,后台 Java 不必多说了,Java 是我的主打专项能力。页面小程序开发也是自己写,从这个时候,我心里就下定决心,我一定要做一名全栈开发工程师,至少目前是这样一个目标。
自己同时做后台和页面开发,虽然精力上会有所分散,也比较忙碌。但是这个过程中,调试其实相当便捷,减少了前后端交互这种日常细节的沟通。后台服务自己写,页面也是自己写,真的可以避免浪费时间在这种日常沟通上,这点还是我非常喜欢的,我本身是一个不太喜欢跟人交互的,总感觉,你在跟人沟通协同处理一件事,是非常费劲的。
未来的目标(唯有热爱,可抵这岁月漫长)
1、始终保持一个健康的体魄和有趣的灵魂。
2、后端仍然是我的主线进阶任务,希望自己能每一天都在进步,争取把后端 Java 做到极致。另外,移动端我也会继续学习相关的技能。
3、业余时间,做一些自己喜欢的事。比如:我最喜欢的吉他,还有看大量的书。

4、希望自己永远积极向上,永远热爱生活,热情奔赴这人间山河,也希望未来能帮助更多的开发者有所成长。

人生苦短,拒绝内卷。我是跟着飞哥学编程,一个一心向阳,向阳而生,努力向上生长的年轻人。加油兄弟们……
相关文章:

关于一名资深Java程序员在移动端的进阶之路
今天呢,就借此机会,跟大家聊一聊我的个人职业经历吧! 那年刚毕业 刚毕业时候,入职的第一家公司,进去后,说实话,没有太大成长吧!基本就是让我做一些可有可无的边缘性的工作ÿ…...

clickonce excel 插件发布安装的原理
ClickOnce 是一种由 Microsoft 提供的部署技术,用于简化和加速Windows应用程序的部署。ClickOnce 可以用于部署各种类型的应用程序,包括 Excel 插件。 以下是 ClickOnce Excel 插件发布和安装的一般原理: 1. 发布应用程序: -…...

关于MySQL Cluster
目录 1.MySQL Cluster2.MySQL Cluster架构3.MySQL Cluster 与 MySQL 主从架构有什么区别4.参考 MySQL Cluster是MySQL的一个高可用性,高性能的分布式数据库解决方案。它结合了内存数据库和共享无状态架构的技术,提供了99.999%的可用性,满足严…...

牵绳遛狗你我他文明家园每一天,助力共建文明社区,基于YOLOv7开发构建公共场景下未牵绳遛狗检测识别系统
遛狗是每天要打卡的事情,狗狗生性活泼爱动,一天不遛就浑身难受,遛狗最重要的就是要拴绳了,牵紧文明绳是养犬人的必修课。外出遛狗时,主人手上的牵引绳更多是狗狗生命健康的一道重要屏障。每天的社区生活中,…...

命令行艺术:简洁指南,效率倍增 | 开源日报 No.136
jlevy/the-art-of-command-line Stars: 141.7k License: NOASSERTION 这个项目是关于命令行的艺术,它提供了一系列有用的笔记和技巧,涵盖了基础知识、日常使用、文件和数据处理以及系统调试等方面。该指南旨在帮助初学者和经验丰富的用户掌握 Bash 命令…...
)
python基础教程五(字典概念和基本操作)
需要将一些列值组合成数据结构并通过编号来访问各个值时,列表很有用。本章介绍一种通过名称来访问各个值的数据结构。这种数据结构称为映射。字典是python中唯一的内置映射类型,其中的值不按顺序排列,而是存储在键下。键可能是数,…...

【Delphi 基础知识 11】重载函数的使用
在Delphi中使用重载函数时,你可以创建多个具有相同名称但参数列表不同的函数。这样,编译器可以根据函数调用时提供的参数类型或数量来确定要调用的具体函数。以下是一个简单的重载函数的例子: unit OverloadExample;interfaceusesSysUtils;t…...

经典目标检测YOLO系列(一)YOLOV1的复现(1)总体架构
经典目标检测YOLO系列(一)实现YOLOV1网络(1)总体架构 实现原版的YOLOv1并没有多大的意义,因此,根据《YOLO目标检测》(ISBN:9787115627094)一书,在不脱离YOLOv1的大部分核心理念的前提下,重构一款较新的YOLOv1检测器,来…...
《设计模式》之策略模式
策略模式定义 比如对象的某个行为,在不同场景有不同实现方式,可以将这些行为的具体实现定义为一组策略,每个实现类实现种策略,在不同场景使用不同的实现,并且可以自由切换策略。 策略模式结构 策略模式需要一个策略…...

Django文章标签推荐
当博客文章实现了标签后,可以用它们做很多有趣的事情。关于标签的更多内容,请看 Django集成第三方标签功能-CSDN博客 使用标签,我们可以很好地对博客文章进行分类。类似主题的帖子会有几个共同的标签。下一步将构建一个功能,以显…...

Git、TortoiseGit进阶
1.安装Git、TortoiseGit和汉化包 Git官网: Git TortoiseGit和汉化包: Download – TortoiseGit – Windows Shell Interface to Git 2.常用命令 创建仓库命令 git init初始化仓库git clone拷贝一份远程仓库,也就是下载一个项目。提交与修改 git add添加文件到暂存区git…...

山区老人爱的礼物丨守护银龄,情暖寒冬
为让山区老人们在寒冷的冬天感受到来自社会的温暖,新年伊始,北京传益千里携手志愿者再次走进酉阳土家族苗族自治县木叶乡分发新的一轮山区老人爱的礼物,让更多的物资走向有需要的人群。 中午阳光正好,志愿者们走进山林中的人家&am…...

【计算机算法设计与分析】n皇后问题(C++_回溯法)
文章目录 题目描述测试样例算法原理算法实现参考资料 题目描述 在nxn格的棋盘上放置彼此不受攻击的n格皇后。按照国际象棋的规则,皇后可以攻击与之处在同一行或同一列或同一斜线上的棋子。n后问题等价于在nxn格的棋盘上放置n个皇后,任何2个皇后不放在同…...

Calendar日历类型常见方法
Calendar日历类型常见方法: 概括:1.get( )方法2、set( ) 设置时间3、常用的add方法4、after()方法表示的时间是否在指定时间之后, before( ) 方法则之前, 返回判断结果4.1、compareTo比较器 概括: Calendar类是一个抽…...

Docker-Compose部署Redis(v7.2)主从模式
文章目录 一、前提准备1. redis配置文件2. 下载redis镜像3. 文件夹结构 二、docker-compose三、主从配置1.主节点配置文件2.从节点配置文件 四、运行五、测试 环境 docker desktop for windows 4.23.0redis 7.2 一、前提准备 1. redis配置文件 因为Redis 7.2 docker镜像里面…...
Spring国际化的应用及原理详解
1. 简介 Spring国际化(Spring Internationalization,简称i18n)是Spring框架提供的一种机制,用于支持多语言的应用程序。它使得开发者能够轻松地在应用程序中实现不同语言的支持,从而满足全球化的需求。通过Spring国际…...

Existing installation is up to date
这个报错是之前安装的docker没有删除干净 解决方法: 打开注册表编辑器 然后再搜索栏:HKEY_LOCAL_MACHINE\SOFTWARE\Microsoft\Windows\CurrentVersion\Uninstall\Docker Desktop 回车 找到Docker Desktop文件夹后,右键删除 重新安装Docker…...
windows安装kafka以及kafka管理工具推荐
windows安装 1.下载地址 下载地址 下载最新版本的.tgz文件解压 2.修改配置 修改config目录下的zookeeper.properties中的dataDir属性 server.properties文件中的log.dir属性 3.启动zookeeper 进入到bin\windows\下的用cmd输入zookeeper-server-start.bat ..\..\config\zo…...
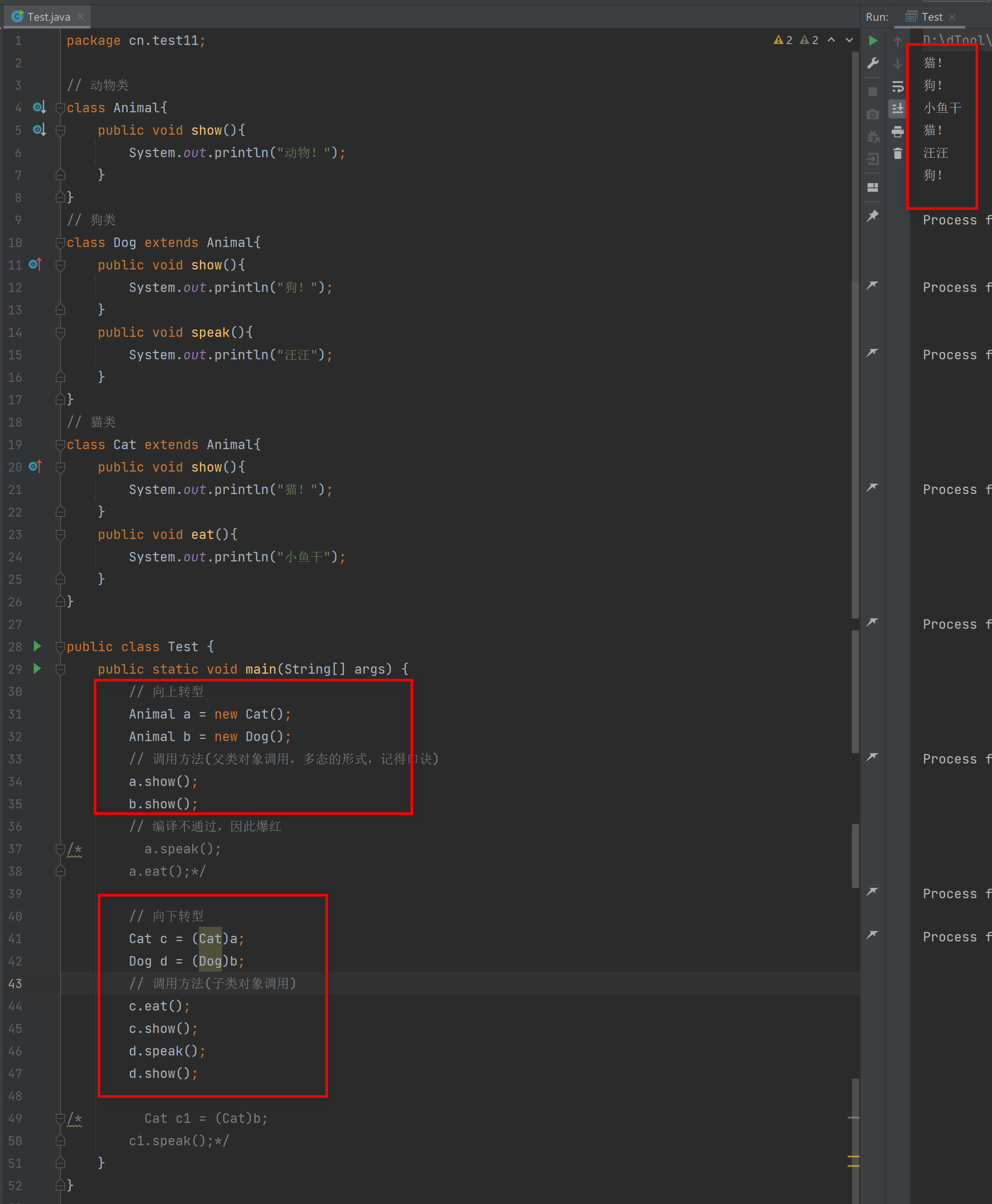
面向对象的三大特征之一多态
多态 概念 多态是同一个对象,在不同时刻表现出来不同的形态,称之为多态。 例如:水,我们把水理解成为一个对象,而水会有不同的形态,比如 液态水、冰块、水蒸气 多态的前提 有继承/实现关系(继承…...
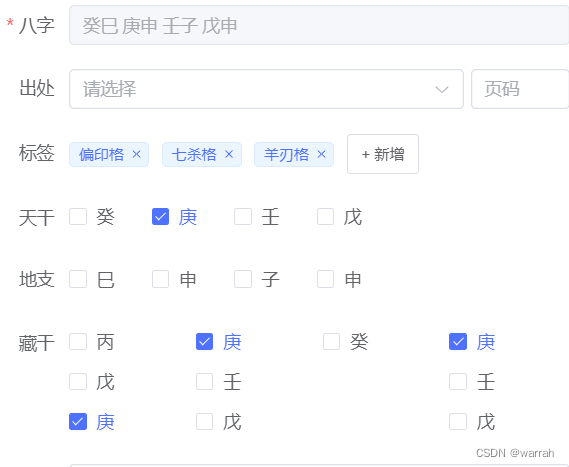
vue3中标签form插件
想写一个系统,对八字进行标注,比如格局,有些八字就有很多格局,于是就想着使用el-tag但是,form表单中如何处理呢? 这个时候,就需要自己写一个,modelValue是表单的默认属性 <template><…...

eNSP-Cloud(实现本地电脑与eNSP内设备之间通信)
说明: 想象一下,你正在用eNSP搭建一个虚拟的网络世界,里面有虚拟的路由器、交换机、电脑(PC)等等。这些设备都在你的电脑里面“运行”,它们之间可以互相通信,就像一个封闭的小王国。 但是&#…...

Robots.txt 文件
什么是robots.txt? robots.txt 是一个位于网站根目录下的文本文件(如:https://example.com/robots.txt),它用于指导网络爬虫(如搜索引擎的蜘蛛程序)如何抓取该网站的内容。这个文件遵循 Robots…...

分布式增量爬虫实现方案
之前我们在讨论的是分布式爬虫如何实现增量爬取。增量爬虫的目标是只爬取新产生或发生变化的页面,避免重复抓取,以节省资源和时间。 在分布式环境下,增量爬虫的实现需要考虑多个爬虫节点之间的协调和去重。 另一种思路:将增量判…...

服务器--宝塔命令
一、宝塔面板安装命令 ⚠️ 必须使用 root 用户 或 sudo 权限执行! sudo su - 1. CentOS 系统: yum install -y wget && wget -O install.sh http://download.bt.cn/install/install_6.0.sh && sh install.sh2. Ubuntu / Debian 系统…...

CSS设置元素的宽度根据其内容自动调整
width: fit-content 是 CSS 中的一个属性值,用于设置元素的宽度根据其内容自动调整,确保宽度刚好容纳内容而不会超出。 效果对比 默认情况(width: auto): 块级元素(如 <div>)会占满父容器…...
多光源(Multiple Lights))
C++.OpenGL (14/64)多光源(Multiple Lights)
多光源(Multiple Lights) 多光源渲染技术概览 #mermaid-svg-3L5e5gGn76TNh7Lq {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-3L5e5gGn76TNh7Lq .error-icon{fill:#552222;}#mermaid-svg-3L5e5gGn76TNh7Lq .erro…...

深度学习水论文:mamba+图像增强
🧀当前视觉领域对高效长序列建模需求激增,对Mamba图像增强这方向的研究自然也逐渐火热。原因在于其高效长程建模,以及动态计算优势,在图像质量提升和细节恢复方面有难以替代的作用。 🧀因此短时间内,就有不…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现企业微信功能
1. 开发环境准备 安装DevEco Studio 3.1: 从华为开发者官网下载最新版DevEco Studio安装HarmonyOS 5.0 SDK 项目配置: // module.json5 {"module": {"requestPermissions": [{"name": "ohos.permis…...

MacOS下Homebrew国内镜像加速指南(2025最新国内镜像加速)
macos brew国内镜像加速方法 brew install 加速formula.jws.json下载慢加速 🍺 最新版brew安装慢到怀疑人生?别怕,教你轻松起飞! 最近Homebrew更新至最新版,每次执行 brew 命令时都会自动从官方地址 https://formulae.…...

【Linux】自动化构建-Make/Makefile
前言 上文我们讲到了Linux中的编译器gcc/g 【Linux】编译器gcc/g及其库的详细介绍-CSDN博客 本来我们将一个对于编译来说很重要的工具:make/makfile 1.背景 在一个工程中源文件不计其数,其按类型、功能、模块分别放在若干个目录中,mak…...
