【MATLAB】【数字信号处理】线性卷积和抽样定理
已知有限长序列:xk=1,2,1,1,0,-3, hk=[1,-1,1]
![]() ,
,
计算离散卷积和yk=xk*h(k)![]() 。
。
程序如下:
function [t,x] = My_conv(x1,x2,t1,t2,dt)
%文件名与函数名对应
%自写的卷积函数
x = conv(x1,x2)*dt;
t0 = t1(1) + t2(1);
L = length(x1) + length(x2)-2;
t = t0:dt:(t0+L*dt);
endclear;
k1 = [0, 1, 2, 3, 4, 5]; %xk的序列号
xk = [1, 2, 1, 1, 0, -3]; %xk的序列值
subplot(311);
stem(k1,xk,'filled');
title('x(k) = [1,2,1,1,0,-3]');
k2 = [0, 1, 2];
hk = [1, -1, 1];
subplot(312);
stem(k2, hk,'filled');
title('h(k) = [1,-1,1]');
[k3,yk] = My_conv(xk, hk, k1, k2, 1); %调用卷积的函数
subplot(313);
stem(k3,yk,'filled');
title('y(k) 卷积后图像');
运行结果如下:

用MATLAB实现对信号xt=cos(2π×20t)![]() 的抽样。
的抽样。
代码如下:
clear;
Signal_Frequency = 20; %信号频率
Signal_Ts = 0.001; %信号的采样间隔
t = 0 : Signal_Ts : 0.1;% fs = 10fc
Sample_Frequency = 1 * Signal_Frequency; %采样频率
Sample_Ts = 1 / Sample_Frequency;%抽样的间隔
xt = cos(2*pi * Signal_Frequency * t);
n = 0 : Sample_Ts : 0.1;
xn = cos(2*pi * Signal_Frequency * n);subplot(321); plot(t,xt); hold on;
stem(n,xn); title('fs = fc');
X1k = fft(xn, Sample_Frequency);
subplot(322); stem(X1k);% fs = 2fc
Sample_Frequency = 2 * Signal_Frequency; %采样频率
Sample_Ts = 1 / Sample_Frequency;%抽样的间隔
xt = cos(2*pi * Signal_Frequency * t);
n = 0 : Sample_Ts : 0.1;
xn = cos(2*pi * Signal_Frequency * n);
subplot(323); plot(t,xt); hold on;
stem(n,xn); title('fs = 2fc');
X10k = fft(xn, Sample_Frequency);
subplot(324); stem(X10k); title('fs = 2fc频谱');% fs = 10fc
Sample_Frequency = 10 * Signal_Frequency; %采样频率
Sample_Ts = 1 / Sample_Frequency;%抽样的间隔
xt = cos(2*pi * Signal_Frequency * t);
n = 0 : Sample_Ts : 0.1;
xn = cos(2*pi * Signal_Frequency * n);
subplot(325); plot(t,xt); hold on;
stem(n,xn); title('fs = 10fc')
X10k = fft(xn, Sample_Frequency);
subplot(326); stem(X10k); title('fs = 10fc频谱');
运行结果如下:

已知序列[xk]={1,1,1}![]() ,对其频谱X(ejΩ)
,对其频谱X(ejΩ)![]() 进行抽样,分别取N=2,3,10观察频域抽样造成的混叠现象。
进行抽样,分别取N=2,3,10观察频域抽样造成的混叠现象。
代码如下:
clear;
xn = [1, 1, 1];X2k = fft(xn,2);
subplot(311);
stem(X2k,'filled');X3k = fft(xn,3);
subplot(312);
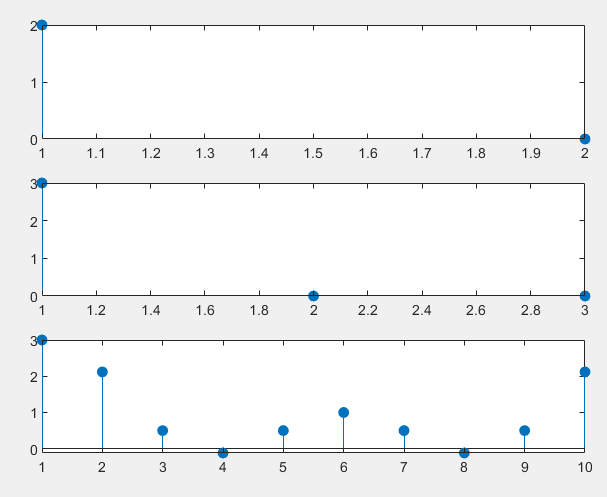
stem(X3k,'filled');X10k = fft(xn, 10);
subplot(313);
stem(X10k,'filled');运行结果如下:
相关文章:

【MATLAB】【数字信号处理】线性卷积和抽样定理
已知有限长序列:xk1,2,1,1,0,-3, hk[1,-1,1] , 计算离散卷积和ykxk*h(k) 。 程序如下: function [t,x] My_conv(x1,x2,t1,t2,dt) %文件名与函数名对应 %自写的卷积函数 x conv(x1,x2)*dt; t0 t1(1) t2(1); L length(x1) length(x2)-2; t t0:dt…...

什么是 MVVM ?
课堂笔记 什么是 MVVM ? MVVM 是一种架构模式,它最初是由微软的两位工程师在 2005 年的时候所提出的。 Model:Model代表的是你的数据View:视图,直接和用户打交道的ViewModel:ViewModel 是 View 和 Model…...
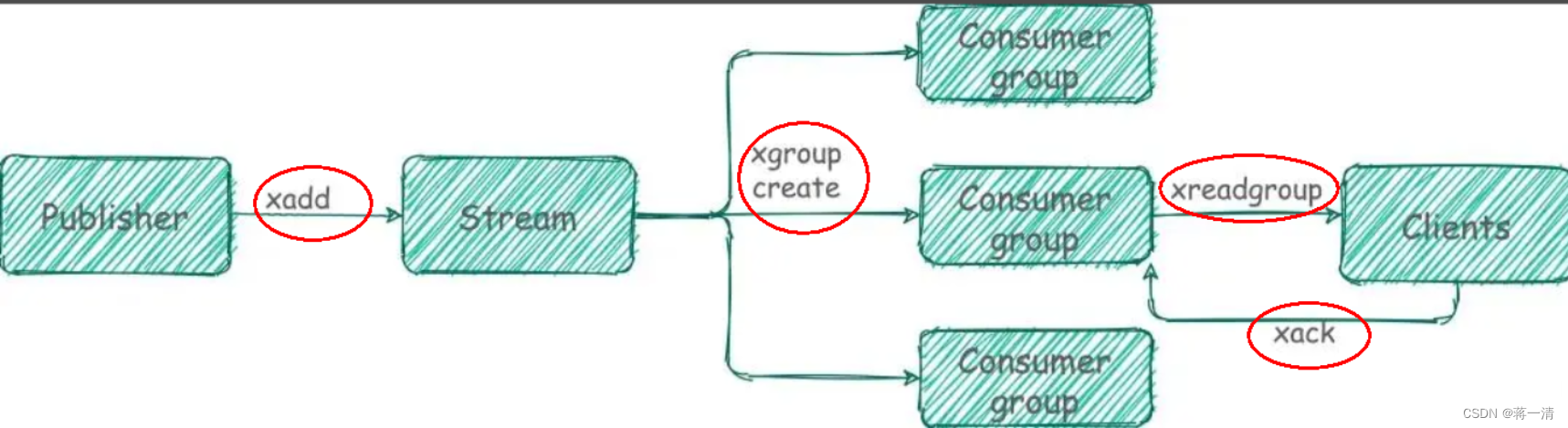
Redis(一)
1、redis Redis是一个完全开源免费的高性能(NOSQL)的key-value数据库。它遵守BSD协议,使用ANSI C语言编写,并支持网络和持久化。Redis拥有极高的性能,每秒可以进行11万次的读取操作和8.1万次的写入操作。它支持丰富的数…...
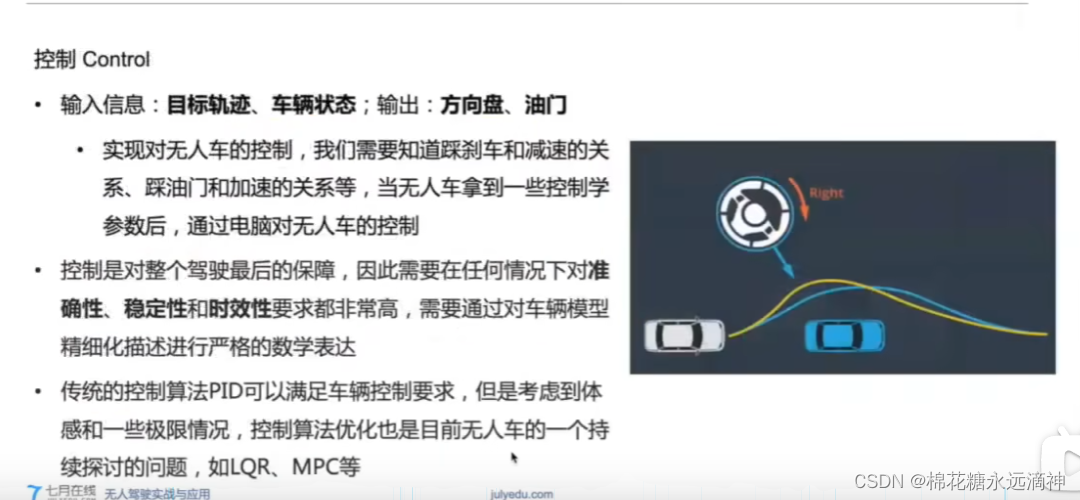
自动驾驶预测-决策-规划-控制学习(1):自动驾驶框架、硬件、软件概述
文章目录 前言:无人驾驶分级一、不同level的无人驾驶实例分析1.L2级别2.L3级别3.L4级别①如何在减少成本的情况下,实现类似全方位高精度的感知呢?②路侧终归是辅助,主车的智能才是重中之重:融合深度学习 二、无人驾驶的…...
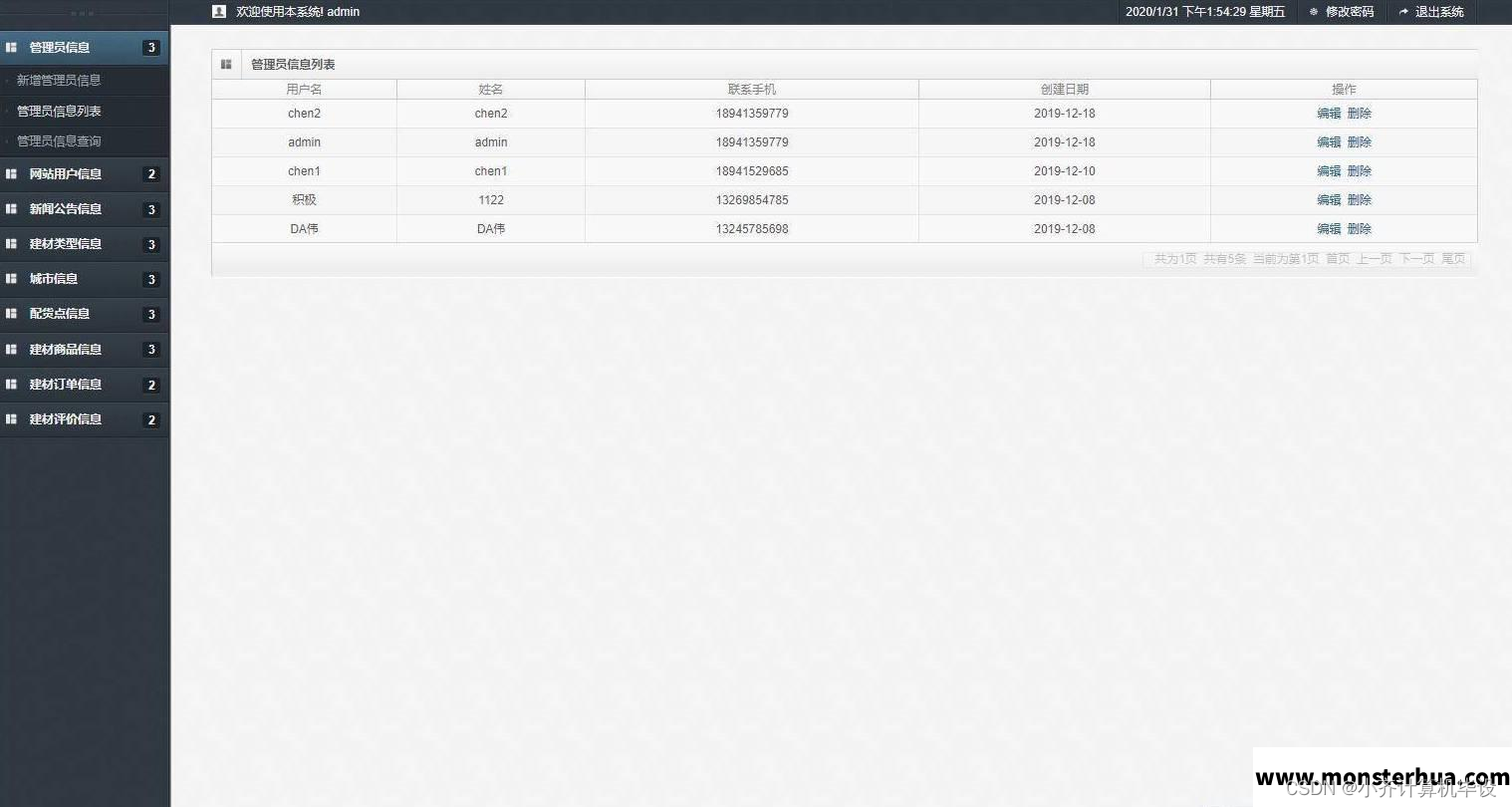
SSM建材商城网站----计算机毕业设计
项目介绍 本项目分为前后台,前台为普通用户登录,后台为管理员登录; 管理员角色包含以下功能: 管理员登录,管理员管理,注册用户管理,新闻公告管理,建材类型管理,配货点管理,建材商品管理,建材订单管理,建材评价管理等功能。 用…...

js逆向第9例:猿人学第2题-js混淆-动态cookie1
题目2:提取全部5页发布日热度的值,计算所有值的加和,并提交答案 (感谢蔡老板为本题提供混淆方案) 既然题目已经给出了cookie问题,那就从cookie入手,控制台找到数据请求地址 可以看到如下加密字符串m类似md5,后面跟着时间戳 m=45cc41dcdb15159ebb50564635f8e362|1704301…...
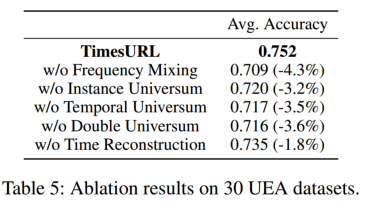
[论文分享]TimesURL:通用时间序列表示学习的自监督对比学习
论文题目:TimesURL: Self-supervised Contrastive Learning for Universal Time Series Representation Learning 论文地址:https://arxiv.org/abs/2312.15709 代码地址:暂无 摘要 学习适用于各种下游任务的通用时间序列表示具有挑战性&…...
解决sublime中文符号乱码问题
效果图 原来 后来 问题不是出自encode文件编码,而是win10的字体问题。 解决方法 配置: { "font_face":"Microsoft Yahei", "dpi_scale": 1.0 } 参考自 Sublime 输入中文显示方框问号乱码_sublime中文问号-CSDN博…...

厚积薄发11年,鸿蒙究竟有多可怕
12月20日中国工程院等权威单位发布《2023年全球十大工程成就》。本次发布的2023全球十大工程成就包括“鸿蒙操作系统”在内。入围的“全球十大工程成就”,主要指过去五年由世界各国工程科技工作者合作或单独完成且实践验证有效的,并且已经产生全球影响…...
 pyDAL查询操作)
pyDAL一个python的ORM(4) pyDAL查询操作
1 、简单查询 rows db(db.person.dept marketing).select(db.person.id, db.person.name, db.person.dept) rows db(db.person.dept marketing).select() rows db(db.person.dept marketing).select(db.person.ALL) rows db().select(db.person.ALL) / db(db.person).se…...

如何通过Python将各种数据写入到Excel工作表
在数据处理和报告生成等工作中,Excel表格是一种常见且广泛使用的工具。然而,手动将大量数据输入到Excel表格中既费时又容易出错。为了提高效率并减少错误,使用Python编程语言来自动化数据写入Excel表格是一个明智的选择。Python作为一种简单易…...
跟着cherno手搓游戏引擎【2】:日志系统spdlog和premake的使用
配置: 日志库文件github: GitHub - gabime/spdlog: Fast C logging library. 新建vendor文件夹 将下载好的spdlog放入 配置YOTOEngine的附加包含目录: 配置Sandbox的附加包含目录: 包装spdlog: 在YOTO文件夹下创建…...
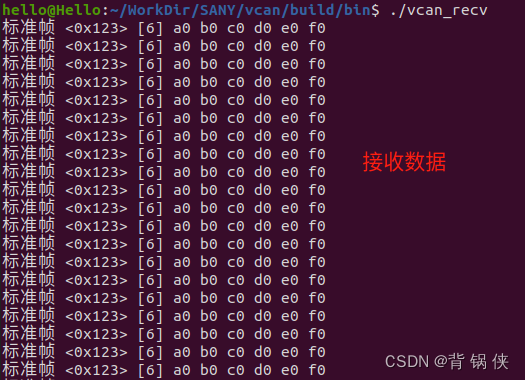
Ubuntu20.04 上启用 VCAN 用作本地调试
目录 一、启用本机的 VCAN 编辑 1.1 加载本机的 vcan 1.2 添加本机的 vcan0 1.3 查看添加的 vcan0 1.4 开启本机的 vcan0 1.5 关闭本机的 vcan0 1.6 删除本机的 vcan0 二、测试本机的 VCAN 2.1 CAN 发送数据 代码 2.2 CAN 接收数据 代码 2.3 CMakeLists.…...

LeetCode(31) 下一个排列
整数数组的一个 排列 就是将其所有成员以序列或线性顺序排列。 例如,arr [1,2,3] ,以下这些都可以视作 arr 的排列:[1,2,3]、[1,3,2]、[3,1,2]、[2,3,1] 。 整数数组的 下一个排列 是指其整数的下一个字典序更大的排列。更正式地…...
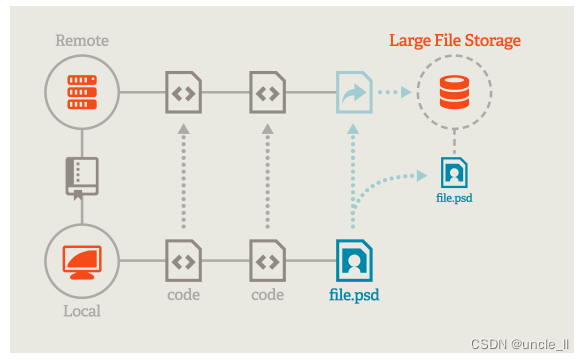
Git LFS: 简单高效的大文件版本控制
Git Large File Storage 问题 在使用git上传大文件时候,git push时候会报错: remote: error: File xxx.tar.gz is 135.17 MB; this exceeds GitHubs file size limit of 100 MB可以看到,git限制上传大小是100MB,超过的话就会报错ÿ…...

如何培养用户思维
产品开发是根据用户要求建造出系统的过程,产品开发是一项包括需求捕捉、需求分析、设计、实现和测试的系统工程,一般通过某种程序设计语言来实现。然而用户思维能够帮助企业更好地理解市场需求,进行产品的开发和完善,用户是企业产…...
由浅入深理解C#中的事件
目录 本文较长,给大家提供了目录,可以直接看自己感兴趣的部分。 前言有关事件的概念示例 简单示例 标准 .NET 事件模式 使用泛型版本的标准 .NET 事件模式 补充总结 参考前言 前面介绍了C#中的委托,事件的很多部分都与委托…...
 配置文件详解 - server stream服务流)
Nginx(十六) 配置文件详解 - server stream服务流
本篇文章主要讲 ngx_stream_core_module 模块下各指令的使用方法,Nginx默认未配置该模块,需要用“--with-stream”配置参数重新编译Nginx。 worker_processes auto;error_log /var/log/nginx/error.log info;events {worker_connections 1024; }stream…...

Css中默认与继承
initial默认样式: initial 用于设置 Css 属性为默认值 h1 {color: initial; }如display或position不能被设置为initial,因为有默认属性。例如:display:inline inherit继承样式: inherit 用于设置 Css 属性应从父元素继承 di…...

gitee上的vue大屏项目
在 Gitee 上,有几个值得注意的 Vue 大屏项目:vue-big-screen-plugin (Gitee): 这是一个基于 Vue3、Typescript、DataV 和 ECharts5 框架的可视化大屏项目。它使用 .vue 和 .tsx 文件构建界面,并采用新版动态屏幕适配方案。这个项目支持数据的动态刷新渲染,内部的 DataV 和 …...

【大模型RAG】拍照搜题技术架构速览:三层管道、两级检索、兜底大模型
摘要 拍照搜题系统采用“三层管道(多模态 OCR → 语义检索 → 答案渲染)、两级检索(倒排 BM25 向量 HNSW)并以大语言模型兜底”的整体框架: 多模态 OCR 层 将题目图片经过超分、去噪、倾斜校正后,分别用…...

Appium+python自动化(十六)- ADB命令
简介 Android 调试桥(adb)是多种用途的工具,该工具可以帮助你你管理设备或模拟器 的状态。 adb ( Android Debug Bridge)是一个通用命令行工具,其允许您与模拟器实例或连接的 Android 设备进行通信。它可为各种设备操作提供便利,如安装和调试…...

逻辑回归:给不确定性划界的分类大师
想象你是一名医生。面对患者的检查报告(肿瘤大小、血液指标),你需要做出一个**决定性判断**:恶性还是良性?这种“非黑即白”的抉择,正是**逻辑回归(Logistic Regression)** 的战场&a…...

在鸿蒙HarmonyOS 5中实现抖音风格的点赞功能
下面我将详细介绍如何使用HarmonyOS SDK在HarmonyOS 5中实现类似抖音的点赞功能,包括动画效果、数据同步和交互优化。 1. 基础点赞功能实现 1.1 创建数据模型 // VideoModel.ets export class VideoModel {id: string "";title: string ""…...

在rocky linux 9.5上在线安装 docker
前面是指南,后面是日志 sudo dnf config-manager --add-repo https://download.docker.com/linux/centos/docker-ce.repo sudo dnf install docker-ce docker-ce-cli containerd.io -y docker version sudo systemctl start docker sudo systemctl status docker …...

java 实现excel文件转pdf | 无水印 | 无限制
文章目录 目录 文章目录 前言 1.项目远程仓库配置 2.pom文件引入相关依赖 3.代码破解 二、Excel转PDF 1.代码实现 2.Aspose.License.xml 授权文件 总结 前言 java处理excel转pdf一直没找到什么好用的免费jar包工具,自己手写的难度,恐怕高级程序员花费一年的事件,也…...

剑指offer20_链表中环的入口节点
链表中环的入口节点 给定一个链表,若其中包含环,则输出环的入口节点。 若其中不包含环,则输出null。 数据范围 节点 val 值取值范围 [ 1 , 1000 ] [1,1000] [1,1000]。 节点 val 值各不相同。 链表长度 [ 0 , 500 ] [0,500] [0,500]。 …...

c#开发AI模型对话
AI模型 前面已经介绍了一般AI模型本地部署,直接调用现成的模型数据。这里主要讲述讲接口集成到我们自己的程序中使用方式。 微软提供了ML.NET来开发和使用AI模型,但是目前国内可能使用不多,至少实践例子很少看见。开发训练模型就不介绍了&am…...

九天毕昇深度学习平台 | 如何安装库?
pip install 库名 -i https://pypi.tuna.tsinghua.edu.cn/simple --user 举个例子: 报错 ModuleNotFoundError: No module named torch 那么我需要安装 torch pip install torch -i https://pypi.tuna.tsinghua.edu.cn/simple --user pip install 库名&#x…...
与常用工具深度洞察App瓶颈)
iOS性能调优实战:借助克魔(KeyMob)与常用工具深度洞察App瓶颈
在日常iOS开发过程中,性能问题往往是最令人头疼的一类Bug。尤其是在App上线前的压测阶段或是处理用户反馈的高发期,开发者往往需要面对卡顿、崩溃、能耗异常、日志混乱等一系列问题。这些问题表面上看似偶发,但背后往往隐藏着系统资源调度不当…...
