数据结构之各大排序(C语言版)
我们这里话不多说,排序重要性大家都很清楚,所以我们直接开始。
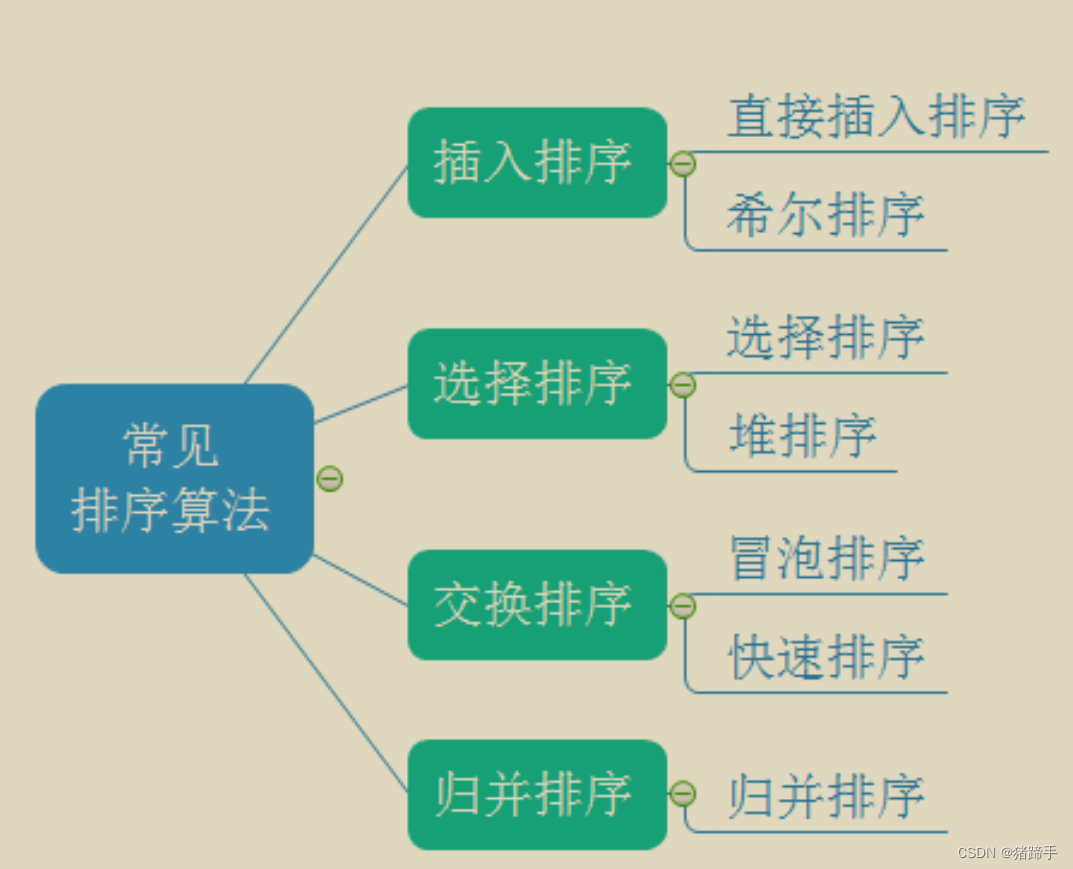
我们就按照这张图来一一实现吧!
一.直接插入排序与希尔排序.
这个是我之前写过的内容了,大家可以通过链接去看看详细内容。
算法之插入排序及希尔排序(C语言版)-CSDN博客
这里就直接赋上代码了
//直接插入排序(升序)
void Insertsort(int* arr, int n)
{for (int i = 0; i < n - 1; i++){int end = i;int tmp = arr[end + 1];while (end >= 0){if (tmp < arr[end]){arr[end + 1] = arr[end];end--;}else{break;}}arr[end + 1] = tmp;}
}//希尔排序(升序)
void Shellsort(int* arr, int n)
{int gap = n;while (gap > 1){gap = gap / 2;//gap = gap / 3 + 1;//先一组组排好//for (int i = 0; i < gap; i++)//{// for (int j = i; j < n - gap; j += gap)// {// int end = j;// int tmp = arr[end + gap];// while (end >= 0)// {// if (tmp < arr[end])// {// arr[end + gap] = arr[end];// end-=gap;// }// else// {// break;// }// }// arr[end + gap] = tmp;// }//}//多组并排for (int i = 0; i < n - gap; i++){int end = i;int tmp = arr[end + gap];while (end >= 0){if (tmp < arr[end]){arr[end + gap] = arr[end];end-=gap;}else{break;}}arr[end + gap] = tmp;}}
}我们还是分析下他们的时间复杂度吧!
插入排序是通过进行比较来插入的,最坏的情况就是都要比较,所以是O(N^2),最好情况就是本生就是顺序且有序的。
而希尔排序则不同,大家现在当下只需知道大概在O(1.3N)左右即可
二.选择排序
选择排序的思想就是:找到最值的两个数,分别放在首尾,然后再选择次一级的,知道排好。是不是非常简单,所以这里我们上代码:
//选择排序(升序)
void Swap(int* p, int* q)
{int* tmp = *p;*p = *q;*q = tmp;
}
void Selectsort(int* arr, int n)
{int begin = 0;int end = n - 1;while (begin < end){int min = begin;int max = begin;for (int i = begin + 1; i <= end; i++){if (arr[i] < arr[min])min = i;if (arr[i] > arr[max])max = i;}Swap(&arr[begin], &arr[min]);//注意:这里一定要留意max的值是不是begin位置,如果是,前一个交换会影响到后一个,所以要找到正确的位置if (max == begin)max = min;Swap(&arr[end], &arr[max]);begin++;end--;}
}三.堆排序
这个之前也实现过了,可以看链接:
堆排序(C语言版)-CSDN博客
这里还是贴下代码:
void Adjustup(int* arr, int child)
{int parent = (child - 1) / 2;while (child > 0){if (arr[child] > arr[parent]){Swap(&arr[child], &arr[parent]);child = parent;parent = (child - 1) / 2;}else{break;}}
}
void Adjustdown(int* arr,int parent, int n)
{int child = parent * 2 + 1;while (child < n){if (child + 1 < n && arr[child + 1] > arr[child]){child++;}if (arr[child] > arr[parent]){Swap(&arr[child], &arr[parent]);parent = child;child = parent * 2 + 1;}else{break;}}
}
//堆排序
void Heapsort(int* arr, int n)
{//建大堆/*for (int i = 1; i < n; i++){Adjustup(arr, i);}*/for (int i = (n - 1 - 1) / 2; i >= 0; i--){Adjustdown(arr,i,n);}//堆删除int end = n - 1;while (end > 0){Swap(&arr[end], &arr[0]);Adjustdown(arr,0, end);end--;}
}四.冒泡排序和快速排序
这是一个可以说是最简单的排序了,实现的关键就是想好两层循环的条件就行了,我之前也实现过了,大家可以去之前我的文章看看,这里给大家一个链接吧!
冒泡排序即相关想法-CSDN博客
这里直接上代码了,学到这还不会冒泡,建议别在看这个文章了,需要去补就前面的了。
//冒泡排序(升序)
void Bubblesort(int* arr, int n)
{for (int i = 0; i < n - 1; i++){for (int j = 0; j < n - i - 1; j++){if (arr[j] > arr[j + 1])Swap(&arr[j], &arr[j + 1]);}}
}时间复杂度:O(N^2)
下面开始我们可以说是非常难的部分了----快速排序
我们先直接学hoare版本吧!
注意:hoare的版本是将key取开头的元素
如果我们按照升序排列,我们要先走右边的,这样才能保证相遇的点其值一定比key点的小,原因如下:
相遇分为以下两种情况:
1.左边相遇右边,即右边停止后左边一直走,没有找到比key大的元素直到相遇,而相遇点是右边找小找到的,说明相遇点比key点小(升序)
2.右边相遇左边,即左边停止后右边一直走,没有找到比key小的元素直到相遇,而相遇点是左边找大找到的,说明相遇点比key点大。(降序)
下面我们实现吧!
//快速排序(升序)
void Swap(int* p, int* q)
{int* tmp = *p;*p = *q;*q = tmp;
}
void Quicksort(int* arr, int begin, int end)//注意end到底是啥?如果是元素个数,下面的right要减1,如果是最后一个元素下标,end=right
{//递归结束条件if (begin >= end)return;int left = begin;int right = end - 1;int key = begin;while (left < right){//先右while (left < right && arr[right] >= arr[key])//右找小{right--;}//再左while (left < right && arr[left] <= arr[key])//左找大{left++;}Swap(&arr[left], &arr[right]);}//相遇点和key交换Swap(&arr[left], &arr[key]);//第一次完成//下面是递归部分key = left;Quicksort(arr, 0, key);Quicksort(arr, key + 1,end);
}这个就是hoare版本了,学到这你可能会问一下问题:
1.为什么左边要找大,右边要找小?
我们如果要排升序,是不是从小到大的顺序,如果交换的左右不是大和小,那么你确定是在排序
2.key为啥就是数组开头元素呢?
这个其实只是hoare版本的key找法,实际上还有其他方法的,下面我们就讲解下其他key找法。
//三数取中法
int Mid(int* arr,int begin, int end)
{int mid = (begin + end-1) / 2;if (arr[begin] > arr[end]){if (arr[mid] > arr[end]){if (arr[begin] > arr[mid])return mid;elsereturn begin;}return end;}else{if (arr[mid] > arr[begin]){if (arr[end] > arr[mid])return mid;elsereturn end;}return begin;}
}对于上面的内容要注意我们都是end表示为最后一个元素是第几个元素,而非所在的数组下标。
下面我们将其改成数组下标,再写一遍hoare版本的快排。
//三数取中法
int Mid(int* arr,int begin, int end)
{int mid = (begin + end) / 2;if (arr[begin] > arr[end]){if (arr[mid] > arr[end]){if (arr[begin] > arr[mid])return mid;elsereturn begin;}return end;}else{if (arr[mid] > arr[begin]){if (arr[end] > arr[mid])return mid;elsereturn end;}return begin;}
}
void Quicksort(int* arr, int begin, int end)//end表示最后一个元素下标
{if (begin >= end)return;int left = begin;int right = end;int key = begin;while (left < right){while (left < right && arr[right] >= arr[key])right--;while (left < right && arr[left] <= arr[key])left++;Swap(&arr[left], &arr[right]);}Swap(&arr[left], &arr[key]);key = left;Quicksort(arr, 0, key - 1);Quicksort(arr, key + 1, end);
}注意改变之处。
大家可能会发现hoare版本的快排有非常多的点需要注意,于是后人就写出了以下两种不同的写法,对其进行改进。
挖坑法
挖坑法是指先将一个数据储存在数组外面,然后还是右边找小,左边找大,找到就将该位置的数放在原先取出的位置,然后现在的位置即是一个新的坑,一直上述操作直到左右相遇,然后将最开始保存的数据放进相遇位置。
下面我们实现它:
//挖坑法
void partQuicksort(int* arr, int begin, int end)//end表示最后一个元素下标
{if (begin >= end)return;int left = begin;int right = end;int key = arr[begin];int hole = begin;//坑while (left < right){while (left < right && arr[right] >= key)right--;arr[hole] = arr[right];hole = right;while (left < right && arr[left] <= key)left++;arr[hole] = arr[left];hole = left;}arr[hole] = key;partQuicksort(arr, begin, hole - 1);partQuicksort(arr, hole + 1, end);
}//前后指针法
void part2Quicksort(int* arr, int begin, int end)//end表示下标
{if (begin >= end)return;int prev = begin;int cur = begin + 1;int key = begin;while (cur <= end){if (arr[cur] < arr[key] && ++prev != cur){Swap(&arr[prev], &arr[cur]);}cur++;}Swap(&arr[prev], &arr[key]);key = prev;part2Quicksort(arr, 0, key - 1);part2Quicksort(arr, key + 1, end);
}对于快排还可以优化,例如:我们这里实现时发现,大部分的递归都是在元素非常小的时候,所以如果我们可以将这部分改成其他排序,是不是可以节省一部分空间。
我们以hoare版本为例:
void Quicksort2(int* arr, int begin, int end)//end表示最后一个元素下标
{if (begin >= end)return;//如果元素小于等于10,利用其他排序,这里我们选择插入排序if (end - begin + 1 <= 10){Insertsort(arr+begin, end - begin + 1);//注意这里数组也要变}else{int left = begin;int right = end;int key = begin;while (left < right){while (left < right && arr[right] >= arr[key])right--;while (left < right && arr[left] <= arr[key])left++;Swap(&arr[left], &arr[right]);}Swap(&arr[left], &arr[key]);key = left;Quicksort(arr, 0, key - 1);Quicksort(arr, key + 1, end);}
}快排学到现在了,大家是不是觉得自己行了???现在我请你实现快排的非递归,请问你如何实现呢?
//快排非递归
int Quicksort3(int* arr, int begin, int end)
{//我们这里就用挖坑法实现int hole = begin;int key = arr[begin];while (begin < end){while (begin < end && arr[end] >= key)end--;arr[hole] = arr[end];hole = end;while (begin < end && arr[begin] <= key)begin++;arr[hole] = arr[begin];hole = begin;}arr[hole] = key;return hole;
}
void QuicksortNone(int* arr, int begin, int end)
{SS s1;StackInit(&s1);StackPush(&s1,begin);StackPush(&s1, end);while (!StackEmpty(&s1)){int right = StackTop(&s1);StackPop(&s1);int left = StackTop(&s1);StackPop(&s1);int key = Quicksort3(arr, left, right);if (left < key - 1){StackPush(&s1, left);StackPush(&s1,key-1);}if (right > key + 1){StackPush(&s1,key+1);StackPush(&s1,right);}}StackDestory(&s1);
}五.归并排序
//归并排序
void _Mergesort(int* arr, int begin, int end, int* tmp)
{if (begin >= end)return;//先递归int mid = (begin + end) / 2;_Mergesort(arr, begin, mid, tmp);_Mergesort(arr, mid + 1, end,tmp);//并int begin1 = begin;int end1 = mid;int begin2 = mid + 1;int end2 = end;int i = begin;while (begin1 <= end1 && begin2 <= end2){if (arr[begin1] < arr[begin2]){tmp[i++] = arr[begin1++];}else{tmp[i++] = arr[begin2++];}}while (begin1 <= end1){tmp[i++] = arr[begin1++];}while (begin2 <= end2){tmp[i++] = arr[begin2++];}memcpy(arr + begin, tmp + begin, (end - begin + 1)*sizeof(int));
}
void MergeSort(int* arr, int n)
{int* tmp = (int*)malloc(sizeof(int) * n);//检查if (tmp == NULL){perror(tmp);return;}_Mergesort(arr, 0, n-1, tmp);free(tmp);tmp = NULL;
}当然,归并排序也可以非递归实现,由于实现过于复杂,所以我们现在就先不是实现了,以后我们会讲的。
大家加油!
相关文章:

数据结构之各大排序(C语言版)
我们这里话不多说,排序重要性大家都很清楚,所以我们直接开始。 我们就按照这张图来一一实现吧! 一.直接插入排序与希尔排序. 这个是我之前写过的内容了,大家可以通过链接去看看详细内容。 算法之插入排序及希尔排序(…...

c++ 中多线程的使用
如果你的其他逻辑必须在线程 t1 和 t2 之后执行,但你又希望这些线程能够同时运行,你可以在主线程中使用 std::thread::detach 将线程分离,让它们在后台运行。这样,主线程不会等待这些线程的完成,而可以继续执行其他逻辑…...
理解二叉树的遍历(算法村第七关白银挑战)
二叉树的前序遍历 144. 二叉树的前序遍历 - 力扣(LeetCode) 给你二叉树的根节点 root ,返回它节点值的 前序 遍历。 示例 1: 输入:root [1,null,2,3] 输出:[1,2,3]解 LeetCode以及面试中提供的方法可能…...
所有单片机使用的汇编语言是统一的吗?
所有单片机使用的汇编语言是统一的吗? 在开始前我有一些资料,是我根据网友给的问题精心整理了一份「单片机的资料从专业入门到高级教程」, 点个关注在评论区回复“888”之后私信回复“888”,全部无偿共享给大家!&…...
C ++类
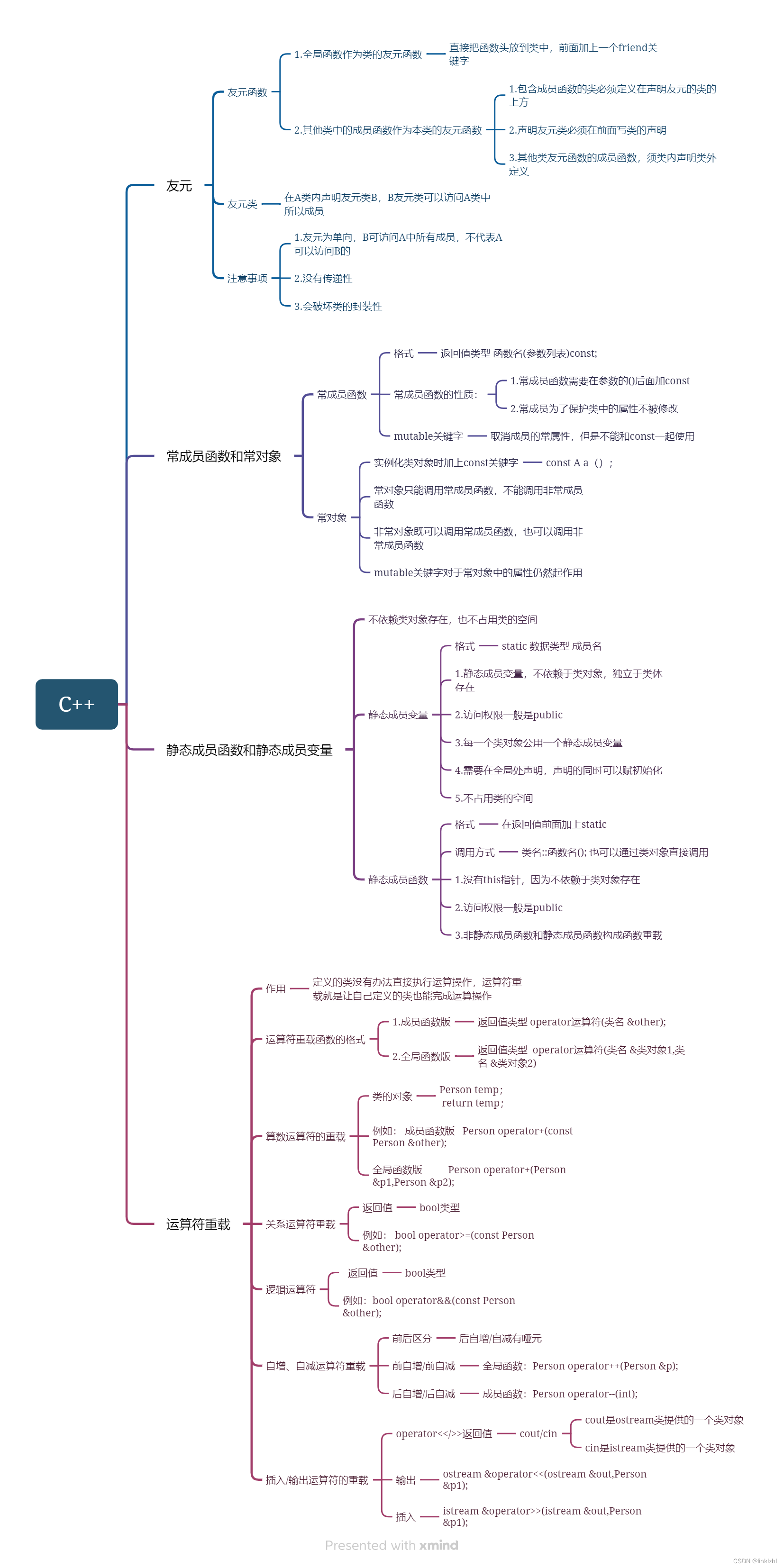
定义一个Person类,私有成员int age,string &name,定义一个Stu类,包含私有成员double *score,写出两个类的构造函数、析构函数、拷贝构造和拷贝赋值函数,完成对Person的运算符重载(算术运算符、条件运算…...
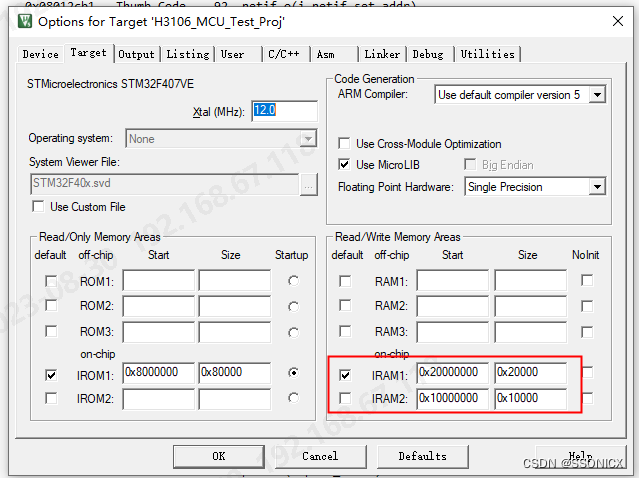
STM32疑难杂症
1.keil的奇怪问题 创建的数组分配内存到0x10000000地址的时候,数据总是莫名其妙的出现问题,取消勾选就正常了 stm32f407内部有一个CCM内存,这部分内存只能由内核控制,任何外设都不能够进行访问。这样问题就来了,如果使…...

GIT使用简介
Git 是一种版本控制系统,常用于团队协作开发和管理代码。下面是 Git 的基本使用方式: 安装 Git:首先,在你的计算机上安装 Git。你可以从 Git 官方网站(https://git-scm.com/)下载适合你操作系统的版本&…...

easycode 插件配置文件
easycode是一个idea生成文件的插件,以下是我的一个项目中配置信息,需要的可以拿走,保存成json文件导入即可 {"author" : "XXX","version" : "1.2.8","userSecure" : "","…...

elasticsearch系列四:集群常规运维
概述 在使用es中如果遇到了集群不可写入或者部分索引状态unassigned,明明写入了很多数据但是查不到等等系列问题该怎么办呢?咱们今天一起看下常用运维命令。 案例 起初我们es性能还跟得上,随着业务发展壮大,发现查询性能越来越不…...
)
6.6 会话与输入事件(三)
三,Pointer会话 3.1 Pointer会话及其属性 指针输入会话使用SCREEN_EVENT_POINTER类型创建,通常用于控制光标的形状和位置。 指针会话的SCREEN_PROPERTY_MODE属性未使用。但是,可以使用下面的会话属性配置指针会话: SCREEN_PROPERTY_ACCELERATION表示一组六个整数,表示x…...

【自动化测试总结】优点、场景、流程、项目人员构成
一、自动化测试的概念 以程序测试程序,以代码代替思维,以脚本的运行代替手工测试,可以大大提高工作测试的效率。 二、自动化测试的优点 1.回归测试更为方便,可靠。自动化测试最主要的任务和特点,特别是在程序修改比较…...
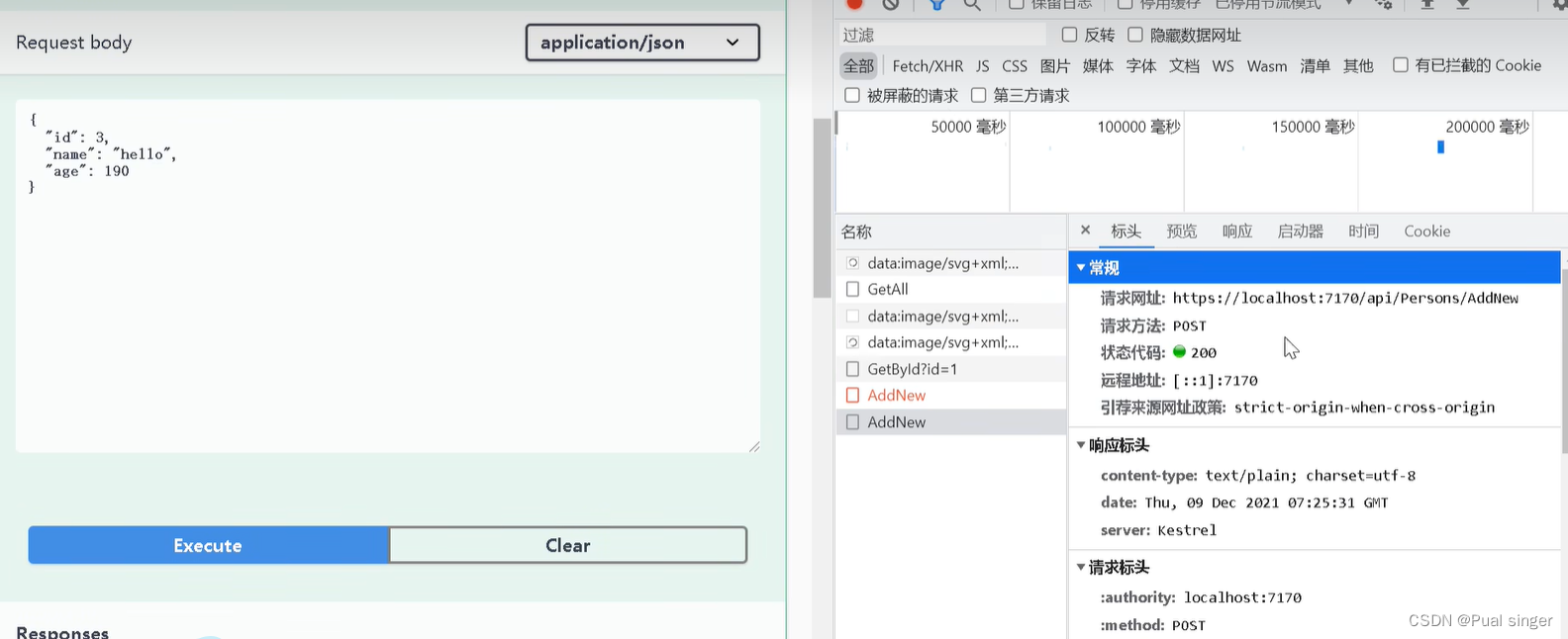
杨中科 ASP.NETCore Rest
什么是Rest RPC 1、Web API两种风格: 面向过程(RPC) 、面向REST (REST) 2、RPC:“控制器/操作方法“的形式把服务器端的代码当成方法去调用。把HTTP当成传输数据的通道,不关心HTTP谓词。通过QueryString请求报文体给服务器传递数据。状态码。比如/Persons/GetAll…...

RTU数据采集终端
在现代工业控制系统中,数据采集是一个至关重要的步骤。RTU(远程终端单元)作为一种常用的数据采集终端设备,不仅可以实现数据的采集和传输,还可以实现现场设备的远程监控和控制。 一、RTU数据采集终端的工作原理 RTU数据采集终端是一种将现场…...

双指针--- 数组元素的目标和
目录 数组元素的目标和思路:暴力做法思路:双指针做法: 代码: 原题链接 数组元素的目标和 给定两个升序排序的有序数组 A 和 B ,以及一个目标值 x 。 数组下标从 0 开始。 请你求出满足 A[i]B[j]x 的数对 (i,j) 。 数据保证有唯…...
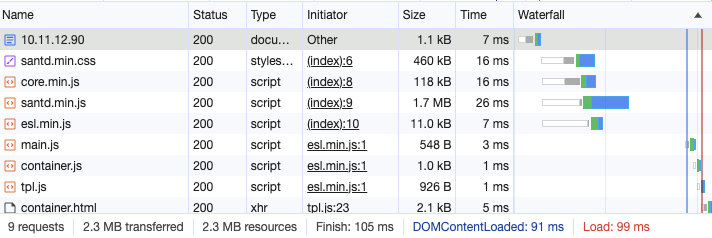
你的网站或许不需要前端构建(二)
前一阵,有朋友问我,能否在不进行前端编译构建的情况下,用现代语法开发网站界面。 于是,就有了这篇文章中提到的方案。 写在前面 这篇文章,依旧不想讨论构建或不构建,哪一种方案对开发更友好,…...

flutter 使用adb 同时连接 多个模拟器
MUMU模拟器 MuMu模拟器官网_安卓12模拟器_网易手游模拟器 传统只需要 连接一个 默认命令是 默认端口是7555 adb connect 127.0.0.1:7555 但是需要同时连接调试多个模拟器的时候 就需要连接多个 这里可以使用自带的多开 多开后 使用 1 是对应多开的序号 这样就可以查看对…...
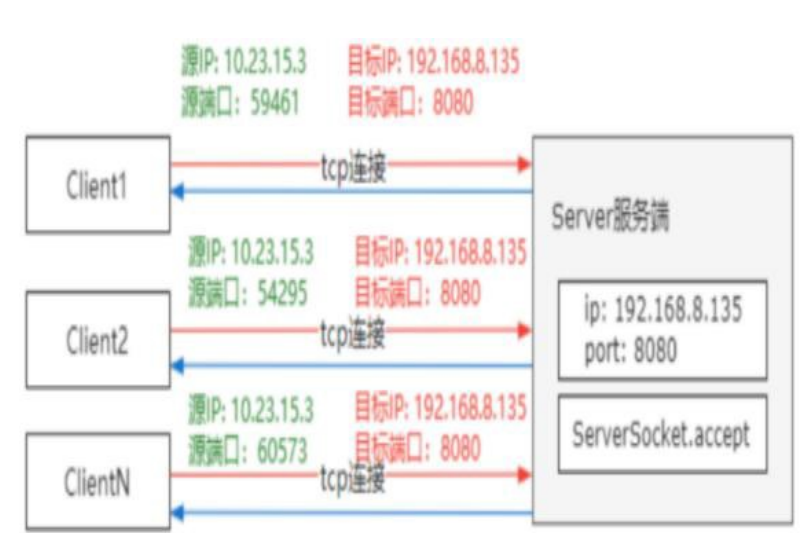
网络四元组
文章目录 网络四元组 今天我们来聊聊 网络四元组 网络四元组 四元组,简单理解就是在 TCP 协议中,去确定一个客户端连接的组成要素,它包括源 IP 地址、目标 IP 地址、源端口号、目标端口号。 正常情况下,我们对于网络通信的认识可…...

[实践总结] 限制正则表达式匹配次数/时间 防止DoS攻击
思路 1、优化正则表达式 2、正则表达式无法优化的话,可以考虑限制匹配次数,或者限制匹配时间 限制 匹配次数 public class CountedCharSequence implements CharSequence {private final CharSequence charSequence;private long count;public Counte…...

ffmpeg 5.0版本调试 ffmpeg 5.01 static版本
ffmpeg 5.0版本调试 写法:ffmpeg -rtsp_transport tcp -re -i rtsp://admin:BYTtest2019192.168.1.2:554/h264/ch1/main/av_stream -q 5 -f mpegts -fflags nobuffer -c:v mpeg1video -an -s 960x540 http://127.0.0.1:12345/demo本地写法 ffmpeg -timeout 5000000…...

应用在游戏机触摸屏中的触摸感应芯片
触屏游戏机的屏幕是由液晶屏和触控层组成的。触控层分为电容式触屏和电阻式触屏两种。电容式触屏是将悬空电极和屏幕玻璃上的电极组成静电场,当人体接近屏幕时,就会改变静电场分布,从而实现触摸的位置探测。而电阻式触屏则是利用玻璃上的两层电极之间通电形成一个电阻值,当手指…...

【Python】 -- 趣味代码 - 小恐龙游戏
文章目录 文章目录 00 小恐龙游戏程序设计框架代码结构和功能游戏流程总结01 小恐龙游戏程序设计02 百度网盘地址00 小恐龙游戏程序设计框架 这段代码是一个基于 Pygame 的简易跑酷游戏的完整实现,玩家控制一个角色(龙)躲避障碍物(仙人掌和乌鸦)。以下是代码的详细介绍:…...

Robots.txt 文件
什么是robots.txt? robots.txt 是一个位于网站根目录下的文本文件(如:https://example.com/robots.txt),它用于指导网络爬虫(如搜索引擎的蜘蛛程序)如何抓取该网站的内容。这个文件遵循 Robots…...

什么是EULA和DPA
文章目录 EULA(End User License Agreement)DPA(Data Protection Agreement)一、定义与背景二、核心内容三、法律效力与责任四、实际应用与意义 EULA(End User License Agreement) 定义: EULA即…...

LLM基础1_语言模型如何处理文本
基于GitHub项目:https://github.com/datawhalechina/llms-from-scratch-cn 工具介绍 tiktoken:OpenAI开发的专业"分词器" torch:Facebook开发的强力计算引擎,相当于超级计算器 理解词嵌入:给词语画"…...

Spring AI 入门:Java 开发者的生成式 AI 实践之路
一、Spring AI 简介 在人工智能技术快速迭代的今天,Spring AI 作为 Spring 生态系统的新生力量,正在成为 Java 开发者拥抱生成式 AI 的最佳选择。该框架通过模块化设计实现了与主流 AI 服务(如 OpenAI、Anthropic)的无缝对接&…...

力扣-35.搜索插入位置
题目描述 给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。 请必须使用时间复杂度为 O(log n) 的算法。 class Solution {public int searchInsert(int[] nums, …...

python报错No module named ‘tensorflow.keras‘
是由于不同版本的tensorflow下的keras所在的路径不同,结合所安装的tensorflow的目录结构修改from语句即可。 原语句: from tensorflow.keras.layers import Conv1D, MaxPooling1D, LSTM, Dense 修改后: from tensorflow.python.keras.lay…...

基于Java+MySQL实现(GUI)客户管理系统
客户资料管理系统的设计与实现 第一章 需求分析 1.1 需求总体介绍 本项目为了方便维护客户信息为了方便维护客户信息,对客户进行统一管理,可以把所有客户信息录入系统,进行维护和统计功能。可通过文件的方式保存相关录入数据,对…...

站群服务器的应用场景都有哪些?
站群服务器主要是为了多个网站的托管和管理所设计的,可以通过集中管理和高效资源的分配,来支持多个独立的网站同时运行,让每一个网站都可以分配到独立的IP地址,避免出现IP关联的风险,用户还可以通过控制面板进行管理功…...

简单介绍C++中 string与wstring
在C中,string和wstring是两种用于处理不同字符编码的字符串类型,分别基于char和wchar_t字符类型。以下是它们的详细说明和对比: 1. 基础定义 string 类型:std::string 字符类型:char(通常为8位)…...
