【机器学习:欧氏距离 】机器学习中欧氏距离的理解和应用
【机器学习:欧氏距离 】机器学习中欧氏距离的理解和应用
- 距离公式
- 二维
- 更高的维度
- 点以外的物体
- 属性
- 欧几里得距离的平方
- 概括
- 历史
在数学中,'欧氏距离’是指欧氏空间中任意两点之间的直线距离。这种距离可以通过应用勾股定理来计算,利用两点的笛卡尔坐标确定它们之间的直线距离,因此有时被称为‘勾股定理距离’。
这些名字来自古希腊数学家欧几里得和毕达哥拉斯。在以欧几里得几何原理为代表的希腊演绎几何中,距离并不表示为数字,而是相同长度的线段被认为是“相等的”。距离的概念是用于绘制圆的圆规工具中固有的,圆的所有点到公共中心点的距离都相同。毕达哥拉斯定理与距离计算的联系直到 18 世纪才建立起来。
两个非点对象之间的距离通常定义为距两个对象的点对之间的最小距离。众所周知,公式用于计算不同类型对象之间的距离,例如从点到线的距离。在高等数学中,距离的概念已被推广到抽象的度量空间,并且已经研究了欧几里得以外的其他距离。在统计和优化的某些应用中,使用欧几里德距离的平方而不是距离本身。

距离公式
实线上任意两点之间的距离是它们坐标数值差的绝对值,即它们的绝对差。因此,如果 p p p和 q q q是实线上的两点,则它们之间的距离由以下公式给出:
d ( p , q ) = ∣ p − q ∣ d(p, q) = |p-q| d(p,q)=∣p−q∣
一个更复杂的公式,给出相同的值,但更容易推广到更高的维度,是:
d ( p , q ) = ( p − q ) 2 d(p, q) = \sqrt{(p-q)^2} d(p,q)=(p−q)2
在此公式中,先平方再开平方会使任何正数保持不变,但用其绝对值替换任何负数。
二维
在二维欧氏空间中,假设点p的笛卡尔坐标为 ( p 1 , p 2 ) (p_1, p_2) (p1,p2),点q的坐标为 ( q 1 , q 2 ) (q_1, q_2) (q1,q2)。然后 p p p和 q q q之间的距离由下式给出:
d ( p , q ) = ( p 1 − q 1 ) 2 + ( p 2 − q 2 ) 2 d(p, q) = \sqrt{(p_1-q_1)^2+(p_2-q_2)^2} d(p,q)=(p1−q1)2+(p2−q2)2
这个距离的计算可以通过将勾股定理应用于一个直角三角形,其中p到q的线段是斜边,而其余两边分别平行于坐标轴平方根内的两个平方公式给出水平边和垂直边上的正方形面积,外平方根将斜边上的正方形面积转换为斜边的长度。
同样,我们也可以计算出两点在极坐标系中的欧氏距离。如 p p p的极坐标是 ( r , θ ) (r, \theta) (r,θ)且 q q q的极坐标 ( s , ψ ) (s, \psi) (s,ψ)是 ,则它们的距离由余弦定律[2]给出:
d ( p , q ) = r 2 + s 2 − 2 r s cos ( θ − ψ ) d(p, q) = \sqrt{r^2+s^2-2rs\cos{(\theta-\psi)}} d(p,q)=r2+s2−2rscos(θ−ψ)
When p p p and q q q are expressed as complex numbers in the complex plane, the same formula for one-dimensional points expressed as real numbers can be used, although here the absolute value sign indicates the complex norm:[4]
d ( p , q ) = ∣ p − q ∣ d(p, q) = |p-q| d(p,q)=∣p−q∣
更高的维度
在三维欧氏空间中,如果点的位置由笛卡尔坐标给出,那么两点之间的距离可以表示为
d ( p , q ) = ( p 1 − q 1 ) 2 + ( p 2 − q 2 ) 2 + ( p 3 − q 3 ) 2 d(p, q) = \sqrt{(p_1-q_1)^2+(p_2-q_2)^2 + (p_3-q_3)^2} d(p,q)=(p1−q1)2+(p2−q2)2+(p3−q3)2
通常,对于在维欧几里得空间中由笛卡尔坐标给出的点,距离为。
d ( p , q ) = ( p 1 − q 1 ) 2 + ( p 2 − q 2 ) 2 + ⋯ + ( p n − q n ) 2 d(p, q) = \sqrt{(p_1-q_1)^2+(p_2-q_2)^2 +\dots + (p_n-q_n)^2} d(p,q)=(p1−q1)2+(p2−q2)2+⋯+(pn−qn)2
欧几里得距离也可以用欧几里得向量差的欧几里得范数更紧凑地表示:
d ( p , q ) = ∣ ∣ p − q ∣ ∣ d(p, q) = ||p-q|| d(p,q)=∣∣p−q∣∣

点以外的物体
对于不是两个点的对象对,距离可以最简单地定义为两个对象之间任意两点之间的最小距离,尽管通常使用从点到集合的更复杂的概括,例如豪斯多夫距离。用于计算不同类型对象之间距离的公式包括:
- 在欧几里得平面中,从点到线的距离。
- 三维欧几里得空间中从点到平面的距离。
- 三维欧几里得空间中两条线之间的距离。
从点到曲线的距离可用于定义其平行曲线,另一条曲线的所有点与给定曲线的距离相同。
属性
欧几里得距离是度量空间中距离的典型示例,它遵循度量空间的所有定义属性:
- 它是对称的,这意味着对于所有点 p p p和 q q q, d ( p , q ) = d ( q , p ) d(p, q)=d(q, p) d(p,q)=d(q,p).也就是说(与单行道的道路距离不同),两点之间的距离不取决于两点中的哪一点是起点,哪一点是终点。
- 它是正数,这意味着每两个不同点之间的距离是一个正数,而从任何一点到自身的距离为零。
- 它服从三角形不等式:每三点 p p p、 q q q和 r r r , d ( p , q ) + d ( q , r ) ≥ d ( p , r ) d(p, q)+d(q, r)\geq d(p, r) d(p,q)+d(q,r)≥d(p,r) 。直观地说,从 p p p经过 q q q到 r r r 旅行不会比直接从 p p p 到 r r r旅行短。
另一个性质,托勒密不等式,涉及四点之间的欧几里得距离 p p p , q q q , r r r 和 s s s 。它指出
d ( p , q ) ⋅ d ( r , s ) + d ( q , r ) ⋅ d ( p , s ) ≥ d ( p , r ) ⋅ d ( q , s ) d(p, q)\cdot d(r, s) + d(q, r)\cdot d(p, s) \geq d(p, r)\cdot d(q,s) d(p,q)⋅d(r,s)+d(q,r)⋅d(p,s)≥d(p,r)⋅d(q,s)
对于平面中的点,这可以改写为,对于每个四边形,四边形相对边的乘积之和至少与其对角线的乘积一样大。然而,托勒密不等式更普遍地适用于欧几里得空间中任何维度的点,无论它们是如何排列的。对于度量空间中不是欧几里得空间的点,这种不等式可能不是真的。欧几里得距离几何研究欧几里得距离的性质,例如托勒密不等式,以及它们在测试给定距离集是否来自欧几里得空间中的点中的应用。
根据贝克曼-夸尔斯定理,欧几里得平面或保持单位距离的高维欧几里得空间的任何变换都必须是等距,保留所有距离。
欧几里得距离的平方
在许多应用中,特别是在比较距离时,在计算欧几里得距离时省略最终平方根可能更方便,因为平方根不会改变顺序(当且仅当)。由此省略产生的值是欧几里得距离的平方,称为欧几里得距离的平方。例如,欧几里得最小生成树可以仅使用距离之间的排序来确定,而不能使用它们的数值。比较平方距离会产生相同的结果,但避免了不必要的平方根计算并回避了数值精度问题。作为一个方程,距离的平方可以表示为平方和:
d 2 ( p , q ) = ( p 1 − q 1 ) 2 + ( p 2 − q 2 ) 2 + ⋯ + ( p n − q n ) 2 d^2(p, q) = (p_1-q_1)^2+(p_2-q_2)^2 +\dots + (p_n-q_n)^2 d2(p,q)=(p1−q1)2+(p2−q2)2+⋯+(pn−qn)2
除了应用于距离比较之外,平方欧几里得距离在统计学中也具有核心重要性,它被用于最小二乘法,这是一种通过最小化观测值和估计值之间的平方距离平均值来将统计估计拟合到数据的标准方法,并且是比较概率分布的最简单的散度形式。彼此之间的平方距离相加,就像在最小二乘拟合中所做的那样,对应于称为勾股加法的(非平方)距离运算。在聚类分析中,可以使用平方距离来增强较长距离的效果。
平方欧几里得距离不形成度量空间,因为它不满足三角形不等式。然而,它是两点的光滑、严格凸函数,与距离不同,距离是非光滑的(靠近相等的点对)和凸但不严格凸的。因此,平方距离在优化理论中是首选,因为它允许使用凸分析。由于平方是非负值的单调函数,因此最小化平方距离等价于最小化欧几里得距离,因此优化问题在两者方面都是等价的,但使用平方距离更容易求解。
有限集合中点对之间的所有平方距离的集合可以存储在欧几里得距离矩阵中,并以这种形式用于距离几何。


概括
在更高级的数学理论中,当把欧氏空间视为一个向量空间时,点之间的距离与一种特殊的范数欧氏范数密切相关。,该范数定义为每个向量与原点的距离。相对于其他规范,该规范的一个重要特性是,在围绕原点的空间任意旋转下,它保持不变。根据德沃雷茨基定理,每个有限维范数向量空间都有一个高维子空间,其范数近似于欧几里得;欧几里得范数是具有此性质的唯一范数。它可以扩展到无限维向量空间,如 L 2 L^2 L2范数或 L 2 L^2 L2距离。欧几里得距离为欧几里得空间提供了拓扑空间的结构,即欧几里得拓扑,以开放球(距给定点小于给定距离的点的子集)作为其邻域。
实坐标空间和函数空间中的其他常见距离:
切比雪夫距离( L ∞ L^\infty L∞ 距离),它测量距离作为每个坐标中距离的最大值。
出租车距离( L 1 L^1 L1距离),也称为曼哈顿距离,它以每个坐标中距离的总和来衡量距离。
闵可夫斯基距离( L p L^p Lp 距离),一种统一欧几里得距离、出租车距离和切比雪夫距离的概括。
对于三维曲面上的点,应将欧几里得距离与测地线距离区分开来,测地线距离是属于曲面的最短曲线的长度。特别是,为了测量地球或其他球形或近球面上的大圆距离,已使用的距离包括哈弗正弦距离,给出球体上两点之间的大圆距离,从它们的经度和纬度,以及文森特公式也称为“文森特距离”,表示椭球体上的距离。

历史
欧几里得距离是欧几里得空间中的距离。这两个概念都以古希腊数学家欧几里得的名字命名,他的《元素》在许多世纪以来成为几何学的标准教科书。长度和距离的概念在各种文化中都很普遍,可以追溯到公元前四千年(远在欧几里得之前)苏美尔现存最早的“原始文盲”官僚文件,并且据推测在儿童中发展的时间早于相关的速度和时间概念。但是,距离的概念,作为从两点定义的数字,实际上并没有出现在欧几里得的元素中。相反,欧几里得通过线段的同余、线段长度的比较以及比例性的概念,隐含地接近了这个概念。
毕达哥拉斯定理也很古老,但只有在勒内·笛卡尔于 1637 年发明笛卡尔坐标后,它才能在距离测量中发挥核心作用。距离公式本身由亚历克西斯·克莱劳特(Alexis Clairaut)于1731年首次发表。由于这个公式,欧几里得距离有时也称为勾股距离。尽管自古以来,许多文化中就再次研究了地球表面长距离的精确测量,这些距离不是欧几里得的(见大地测量学的历史),但欧几里得距离可能不是测量数学空间中点之间距离的唯一方法的想法甚至更晚,随着 19 世纪非欧几里得几何的表述。欧几里得范数和三维以上几何的欧几里得距离的定义也最早出现在 19 世纪的奥古斯丁-路易·柯西 (Augustin-Louis Cauchy) 的著作中。
相关文章:

【机器学习:欧氏距离 】机器学习中欧氏距离的理解和应用
【机器学习:欧氏距离 】机器学习中欧氏距离的理解和应用 距离公式二维更高的维度点以外的物体属性欧几里得距离的平方概括历史 在数学中,欧氏距离’是指欧氏空间中任意两点之间的直线距离。这种距离可以通过应用勾股定理来计算,利用两点的笛卡…...

系统安全及应用
1、基本安全措施 1.1、系统账号清理 在Linux系统中,除了用户手动创建的各种账号之外,还包括随系统或程序安装过程而生产的其他大量账号。除了超级用户root之外,其他大量账号只是用来维护系统运作、启动或保持服务进程,一般是不允…...

Danil Pristupov Fork(强大而易用的Git客户端) for Mac/Windows
在当今软件开发领域,团队协作和版本控制是非常重要的方面。在这个过程中,Git成为了最受欢迎的版本控制工具之一。然而,对于Git的使用,一个好的客户端是至关重要的。 今天,我们要为大家介绍一款强大而易用的Git客户端—…...
最新GPT4.0使用教程,AI绘画,ChatFile文档对话总结+GPT语音对话使用,DALL-E3文生图
一、前言 ChatGPT3.5、GPT4.0、GPT语音对话、Midjourney绘画,文档对话总结DALL-E3文生图,相信对大家应该不感到陌生吧?简单来说,GPT-4技术比之前的GPT-3.5相对来说更加智能,会根据用户的要求生成多种内容甚至也可以和…...

【ARM 嵌入式 编译系列 7.2 -- GCC 链接脚本中 DEFINED 函数与 “AT>“ 符号详细介绍】
文章目录 GCC 链接脚本中 DEFINED 函数DEFINED() 函数> (放置在哪个区域)AT> (加载地址) (填充字节) 在链接脚本中,组合示例 GCC 链接脚本中 DEFINED 函数 在 ARM GCC 链接脚本(.ld 文件)中,DEFINED() 是一种内置函数&…...
Linux基础——进程初识(二)
1. 对当前目录创建文件的理解 我们知道在创建一个文件时,它会被默认创建到当前目录下,那么它是如何知道当前目录的呢? 对于下面这样一段代码 #include <stdio.h> #include <unistd.h>int main() {fopen("tmp.txt", …...

国科大图像处理2024速通期末——汇总2017-2019、2023回忆
国科大2023.12.28图像处理0854期末重点 图像处理 王伟强 作业 课件 资料 一、填空 一个阴极射线管它的输入与输出满足 s r 2 sr^{2} sr2,这将使得显示系统产生比希望的效果更暗的图像,此时伽马校正通常在信号进入显示器前被进行预处理,令p…...
)
编程笔记 html5cssjs 026 HTML输入类型(2/2)
编程笔记 html5&css&js 026 HTML输入类型(2/2) 输入类型:date输入类型:color输入类型:range输入类型:month输入类型:week输入类型:time输入类型:datetime输入类型…...
Vue2 - 数据响应式原理
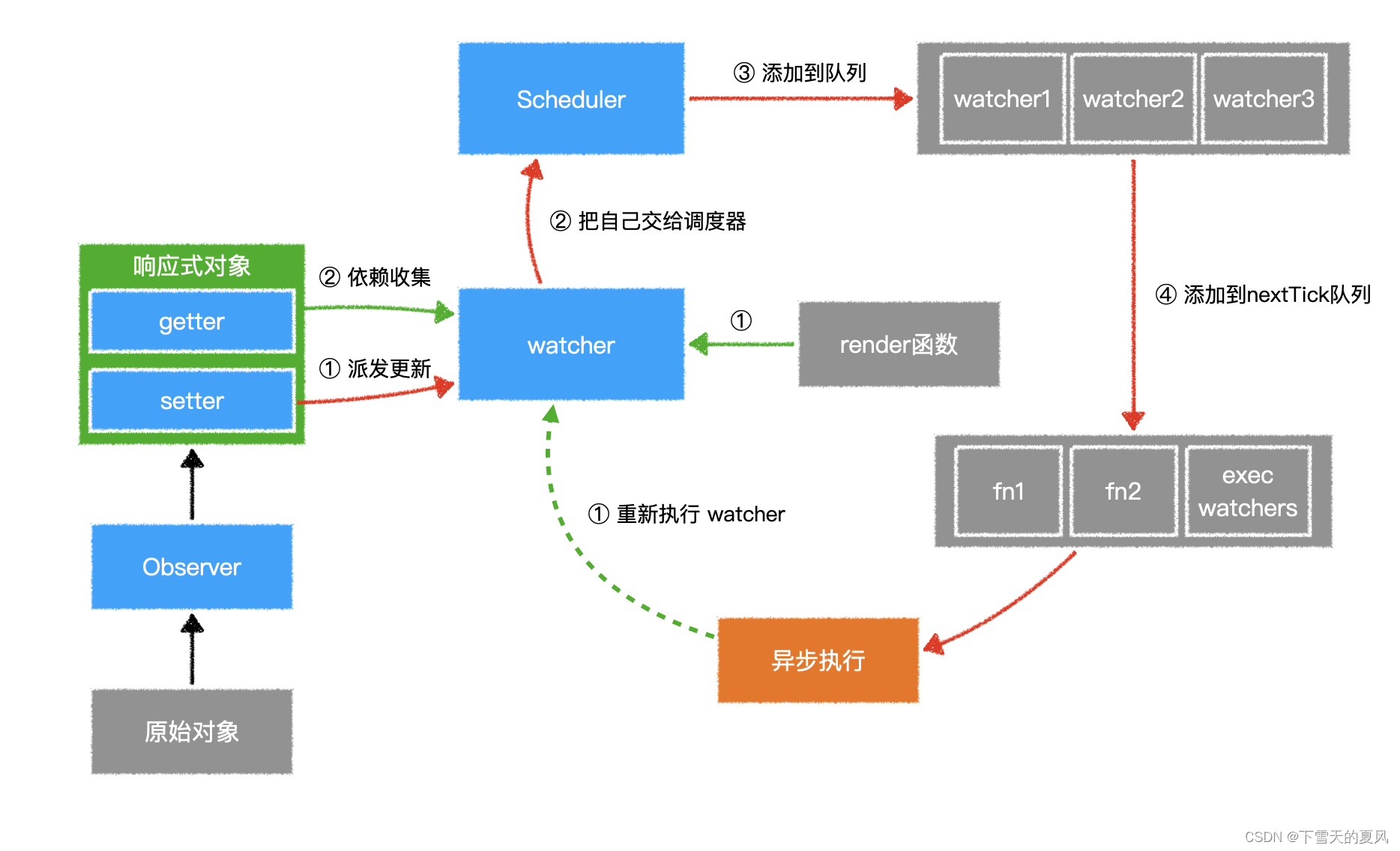
目录 1,总览2,Observer3,Dep4,Watcher5,Schedule 1,总览 vue2官网参考 简单介绍下上图流程:以 Data 为中心来说, Vue 会将传递给 Vue 实例的 data 选项(普通 js 对象&a…...

基于华为云解析服务实现网站区域封禁
前言 中国大陆以外的网络攻击不断,个人博客时常遭受不明个人或组织的攻击,给网站的安全运行带来了巨大的风险,同时DDoS、CC攻击等还会消耗服务器的资源,站长可能需要因此支付高昂的服务器、CDN的流量费用。 因此,如果…...

在 Docker 中配置 MySQL 数据库并初始化 Project 项目
1. 文件准备 1.1. 添加 SQL 文件头部内容 每个 SQL 文件的头部需要添加以下内容: DROP DATABASE IF EXISTS xx_..; CREATE DATABASE xx_..; USE xx_..;1.2. 修改 AUTO_INCREMENT 在每个 SQL 文件中,将 AUTO_INCREMENT 修改为 1。 1.3. 插入机型 在 SQL…...
生活中的物理3——神奇陷阱(随机倒下的抽屉柜门)
1实验 材料:大自然(风)、抽屉门松掉的抽屉 实验 1、找一个大风的日子,打开窗户(不要找下雨天,不然你会被你亲爱的嫲嫲KO) 2、让风在抽屉面前刮过 3、你发现了什么??&…...

数模学习day08-拟合算法
这里拟合算法可以和差值算法对比 引入 插值和拟合的区别 与插值问题不同,在拟合问题中不需要曲线一定经过给定的点。拟 合问题的目标是寻求一个函数(曲线),使得该曲线在某种准则下与所 有的数据点最为接近,即曲线拟…...
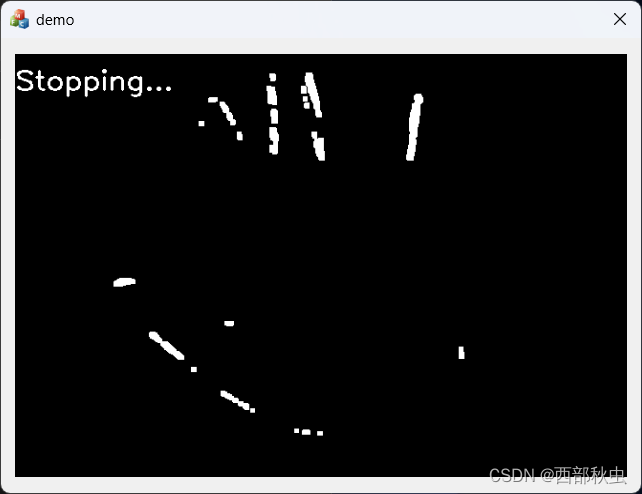
第13课 利用openCV检测物体是否运动了
FFmpeg与openCV绝对是绝配。前面我们已经基本熟悉了FFmpeg的工作流程,这一章我们重点来看看openCV。 在前面,我们已经使用openCV打开过摄像头并在MFC中显示图像,但openCV能做的要远超你的想像,比如可以用它来实现人脸检测、车牌识…...
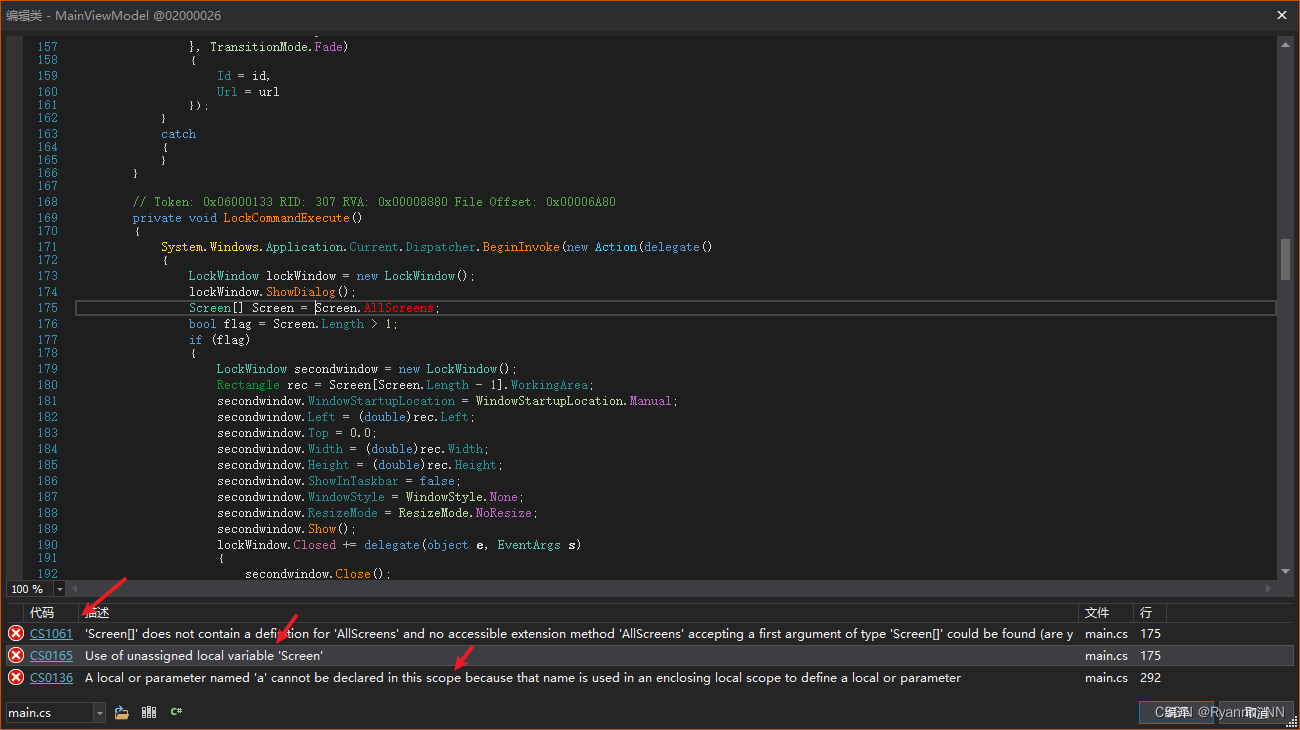
C#之反编译之路(一)
本文将介绍微软反编译神器dnSpy的使用方法 c#反编译之路(一) dnSpy.exe区分64位和32位,所以32位的程序,就用32位的反编译工具打开,64位的程序,就用64位的反编译工具打开(个人觉得32位的程序偏多,如果不知道是32位还是64位,就先用32位的打开试试) 目前只接触到wpf和winform的桌…...

使用CentOS 7.6搭建HTTP隧道代理服务器
在现代网络环境中,HTTP隧道代理服务器因其灵活性和安全性而受到广泛关注。CentOS 7.6,作为一个稳定且功能强大的Linux发行版,为搭建此类服务器提供了坚实的基础。 首先,我们需要明确HTTP隧道代理的基本原理。HTTP隧道代理允许客户…...

Swift爬虫使用代理IP采集唯品会商品详情
目录 一、准备工作 二、代理IP的选择与使用 三、使用Swift编写唯品会商品爬虫 四、数据解析与处理 五、注意事项与优化建议 六、总结 一、准备工作 在开始编写爬虫之前,需要准备一些工具和库,以确保数据抓取的顺利进行。以下是所需的工具和库&…...
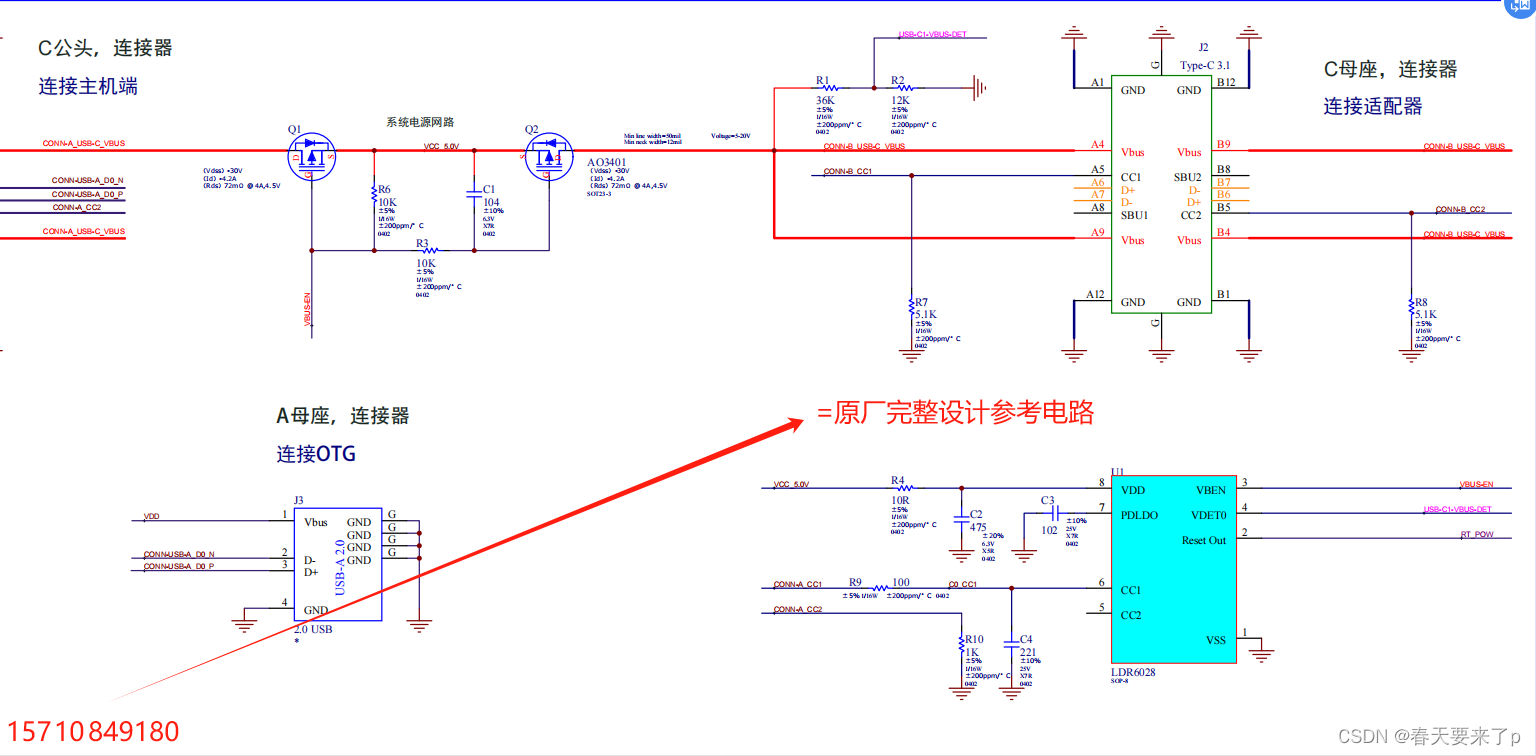
高性价比LDR6028Type-C转3.5mm音频和PD快充转接器
随着市面上的大部分手机逐渐取消了3.5mm音频耳机接口,仅保留一个Type-C接口,追求音质和零延迟的用户面临着一大痛点。对于这些用户,Type-C转3.5mm接口线的出现无疑是一大福音。这款线材在刚推出时就受到了手机配件市场的热烈欢迎,…...
【Docker】docker 服务相关命令
目录 1. 启动docker 服务 2.查看docker 服务的状态 3. 停止docker 服务 4.重启 docker 服务 5.开机自启动命令 1. 启动docker 服务 systemctl start docker 2.查看docker 服务的状态 systemctl status docker 3. 停止docker 服务 systemctl stop docker 此时再使用 syst…...

基于SpringBoot的在线问卷调查系统
文章目录 项目介绍主要功能截图:部分代码展示设计总结项目获取方式🍅 作者主页:超级无敌暴龙战士塔塔开 🍅 简介:Java领域优质创作者🏆、 简历模板、学习资料、面试题库【关注我,都给你】 🍅文末获取源码联系🍅 项目介绍 基于SpringBoot的在线问卷调查系统,java…...

Spark 之 入门讲解详细版(1)
1、简介 1.1 Spark简介 Spark是加州大学伯克利分校AMP实验室(Algorithms, Machines, and People Lab)开发通用内存并行计算框架。Spark在2013年6月进入Apache成为孵化项目,8个月后成为Apache顶级项目,速度之快足见过人之处&…...

简易版抽奖活动的设计技术方案
1.前言 本技术方案旨在设计一套完整且可靠的抽奖活动逻辑,确保抽奖活动能够公平、公正、公开地进行,同时满足高并发访问、数据安全存储与高效处理等需求,为用户提供流畅的抽奖体验,助力业务顺利开展。本方案将涵盖抽奖活动的整体架构设计、核心流程逻辑、关键功能实现以及…...

Xshell远程连接Kali(默认 | 私钥)Note版
前言:xshell远程连接,私钥连接和常规默认连接 任务一 开启ssh服务 service ssh status //查看ssh服务状态 service ssh start //开启ssh服务 update-rc.d ssh enable //开启自启动ssh服务 任务二 修改配置文件 vi /etc/ssh/ssh_config //第一…...

Redis相关知识总结(缓存雪崩,缓存穿透,缓存击穿,Redis实现分布式锁,如何保持数据库和缓存一致)
文章目录 1.什么是Redis?2.为什么要使用redis作为mysql的缓存?3.什么是缓存雪崩、缓存穿透、缓存击穿?3.1缓存雪崩3.1.1 大量缓存同时过期3.1.2 Redis宕机 3.2 缓存击穿3.3 缓存穿透3.4 总结 4. 数据库和缓存如何保持一致性5. Redis实现分布式…...

转转集团旗下首家二手多品类循环仓店“超级转转”开业
6月9日,国内领先的循环经济企业转转集团旗下首家二手多品类循环仓店“超级转转”正式开业。 转转集团创始人兼CEO黄炜、转转循环时尚发起人朱珠、转转集团COO兼红布林CEO胡伟琨、王府井集团副总裁祝捷等出席了开业剪彩仪式。 据「TMT星球」了解,“超级…...

Qwen3-Embedding-0.6B深度解析:多语言语义检索的轻量级利器
第一章 引言:语义表示的新时代挑战与Qwen3的破局之路 1.1 文本嵌入的核心价值与技术演进 在人工智能领域,文本嵌入技术如同连接自然语言与机器理解的“神经突触”——它将人类语言转化为计算机可计算的语义向量,支撑着搜索引擎、推荐系统、…...

如何将联系人从 iPhone 转移到 Android
从 iPhone 换到 Android 手机时,你可能需要保留重要的数据,例如通讯录。好在,将通讯录从 iPhone 转移到 Android 手机非常简单,你可以从本文中学习 6 种可靠的方法,确保随时保持连接,不错过任何信息。 第 1…...

Nginx server_name 配置说明
Nginx 是一个高性能的反向代理和负载均衡服务器,其核心配置之一是 server 块中的 server_name 指令。server_name 决定了 Nginx 如何根据客户端请求的 Host 头匹配对应的虚拟主机(Virtual Host)。 1. 简介 Nginx 使用 server_name 指令来确定…...

重启Eureka集群中的节点,对已经注册的服务有什么影响
先看答案,如果正确地操作,重启Eureka集群中的节点,对已经注册的服务影响非常小,甚至可以做到无感知。 但如果操作不当,可能会引发短暂的服务发现问题。 下面我们从Eureka的核心工作原理来详细分析这个问题。 Eureka的…...

CSS设置元素的宽度根据其内容自动调整
width: fit-content 是 CSS 中的一个属性值,用于设置元素的宽度根据其内容自动调整,确保宽度刚好容纳内容而不会超出。 效果对比 默认情况(width: auto): 块级元素(如 <div>)会占满父容器…...
