1329:【例8.2】细胞 广度优先搜索
1329:【例8.2】细胞
时间限制: 1000 ms 内存限制: 65536 KB
【题目描述】
一矩形阵列由数字0
到9组成,数字1到9
代表细胞,细胞的定义为沿细胞数字上下左右还是细胞数字则为同一细胞,求给定矩形阵列的细胞个数。如:
4 10
0234500067
1034560500
2045600671
0000000089
有4个细胞。
【输入】
第一行为矩阵的行n和列m;
下面为一个n×m的矩阵。
【输出】
细胞个数。
【输入样例】
4 10
0234500067
1034560500
2045600671
0000000089
【输出样例】
4
解析:
题意可知:只要是上下左右相邻都是不为0数字,即为同一种细胞(我第一次读以为只有上下左右有数字不为0,才能算一种细胞emmmm傻狗 )
如果把该二位数组每个位置视为节点,则题目思路如下:
-
可以用深度优先算法:从第一个节点开始遍历,然后分别判断其上下左右是否有相邻的。dfs的精髓就是每次再判断这个节点的数的‘邻居’是否其相邻是同一细胞时,只要是,就立即dfs该‘邻居’,,继续dfs,直到判断完成,又回溯到上一个节点,判断其上下左右。
-
也可以用广度优先算法:从一个节点开始遍历,然后分别判断其上下左右是否是同一种细胞,如果是,则上下左右判断完后,再判断该节点的上下左右(即该节点的上面一个节点)
- 而表示这个遍历了上下左右后再回到该节点就需要用到队列(先进先出)
- 可以用一个结构体队列,将下标(x,y)遍历时入队,然后判断四个方向,如果是同一种细胞则压入队列,四个方向遍历完后,回到队列头部,将其出队(
q.pop()),然后又从队头开始去判断其四个方向,,,,直到该队列为空,说明这一种细胞已经搜索完了(由于队列的顺序性,也可以不用结构体数组,直接分别将x,y分别压入队列,在获取到队头的x后,及时Pop(),也可以通过q.front()拿到y,所以可以不用结构体数组)
-
不管是哪个搜索,都可以在搜索到一个节点时,及时标注(用一个数组去记录是否访问过),减少遍历时间。由于此题特殊,可以直接将数组值设为0,也可以在搜索完成后不会出现二次遍历的情况
代码示例:
深度优先搜索
//深搜-样例比较小时可以用
#include<bits/stdc++.h>
using namespace std;
#define N 101
int n,m,num;
char a[N][N];
int dx[4]={-1,1,0,0}; //上、下、左、右四个方向
int dy[4]={0,0,-1,1};
void dfs(int x,int y);
int main()
{cin>>n>>m; for(int i=0;i<n;i++)scanf("%s",&a[i]);//遍历每个元素,用标记数组标记已经访问过的,则可以避免二次遍历 ,减缩短运行时间 for(int i=0;i<n;i++){for(int j=0;j<m;j++){if(a[i][j]!='0'){num++; //没被访问过说明是新的不同的细胞 dfs(i,j); //搜索这一元素的四个方向}}}cout<<num;return 0;
}
void dfs(int x,int y)
{a[x][y]='0';//为0即也表示该细胞已经访问过了 int newx,newy;for(int i=0;i<4;i++){newx=x+dx[i];newy=y+dy[i];//首先保证在边界内,其次保证他是细胞,最后保证他是未被访问过的 ,都满足即可继续访问其周围的细胞 if(newx<n && newx>=0 && newy<m && newy>=0&&a[newx][newy]!='0') {dfs(newx,newy);}}
}
广度优先搜索
//广搜
#include<bits/stdc++.h>
using namespace std;
#define N 101
int n,m,num;
char a[N][N];
int dx[4]={-1,1,0,0}; //上、下、左、右四个方向
int dy[4]={0,0,-1,1};
queue<int>q;//数据类型为int的队列 -先进先出
void bfs(int x,int y);
int main()
{cin>>n>>m; for(int i=0;i<n;i++)scanf("%s",&a[i]);for(int i=0;i<n;i++){for(int j=0;j<m;j++){if(a[i][j]!='0'){num++; //没被访问过说明是新的不同的细胞 bfs(i,j); //搜索这一元素的四个方向}}}cout<<num;return 0;
}
void bfs(int x,int y)
{a[x][y]='0';//表示访问过 ,在这里不会影响入队后的周围细胞的判断,因为一次bfs就完成了同一个细胞的问题 q.push(x),q.push(y);//将下标分别压入队列(属于同一个细胞队列) int newx,newy;//同一个细胞队列,先拿到队列的数据,出队处理,然后一次访问四个方向(立即出队便于后面同一种细胞进来,保证每次循环处理的是新一个细胞) while(!q.empty()){int nx=q.front(); q.pop();int ny=q.front();q.pop();for(int i=0;i<4;i++){newx=nx+dx[i],newy= ny+dy[i];if(newx<n && newx>=0 && newy<m && newy>=0&&a[newx][newy]!='0') {//继续压入栈(是同一个细胞)q.push(newx);q.push(newy);a[newx][newy]='0';//只是压入同一个细胞的栈,不会继续搜索,所以要标记为以访问,避免重复访问 }}} }
深度优先算法BFS是一种图像搜索演算法,属于一种盲目搜寻法,目的是系统地展开并检查图中的所有节点,主要借助一个队列、一个布尔类型数组、邻接矩阵完成**。
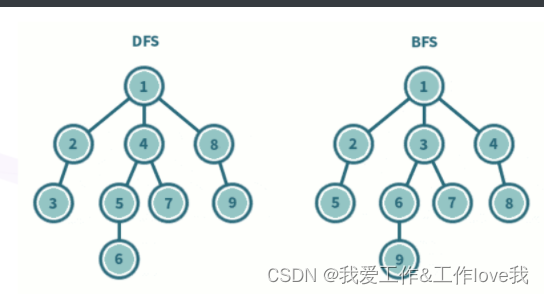
从图像来看,他是先一个节点搜索所有的子节点遍历完毕后,再回到同层次的第一个的节点再次遍历其所有子节点。
在实际运用时,遍历子节点的过程实质是求完一个情况的所有相邻的解,再开始搜索下一个节点
以下是bfs和dfs的树遍历对比
相关文章:

1329:【例8.2】细胞 广度优先搜索
1329:【例8.2】细胞 时间限制: 1000 ms 内存限制: 65536 KB 【题目描述】 一矩形阵列由数字0 到9组成,数字1到9 代表细胞,细胞的定义为沿细胞数字上下左右还是细胞数字则为同一细胞,求给定矩形阵列的细胞个数。如: 4 10 0234500067 1034560500 2045600671 00000000…...

9款免费网络钓鱼模拟器详解
根据《2023年网络钓鱼状况报告》显示,自2022年第四季度至2023年第三季度,网络钓鱼电子邮件数量激增了1265%。其中,利用ChatGPT等生成式人工智能工具和聊天机器人的形式尤为突出。 除了数量上的激增外,网络钓鱼攻击模式也在不断进…...

linux cpu、memory 、io、网络、文件系统多种类型负荷模拟调测方法工具
目录 一、概述 二、stress介绍和使用 2.1 介绍 2.2 使用 三、stress-ng介绍和使用 3.1 介绍 3.2 使用 3.3 实例 四、sysbench 4.1 介绍 4.2 使用 五、lmbench 5.1 介绍 5.2 使用 一、概述 今天介绍两款cpu负荷调试工具,用来模拟多种类型的负载。主要用来模拟CPU…...
1018:奇数偶数和1028:I love 闰年!和1029:三角形判定
1018:奇数偶数 要求:输入一个整数,判断该数是奇数还是偶数。如果该数是奇数就输出“odd”,偶数就输出“even”(输出不含双引号)。 输入样例:8 输出样例:even 程序流程图:…...

数据密集型应用系统设计--第2章 数据模型与查询语言
一、引言 数据模型可能是开发软件最重要的部分,而且还对如何思考待解决的问题都有深远的影响。 大多数应用程序是通过一层一层叠加数据模型来构建的。每一层都面临的关键问题是:如何将其用下一层来表示? 1.作为一名应用程序开发人员,观测现实…...
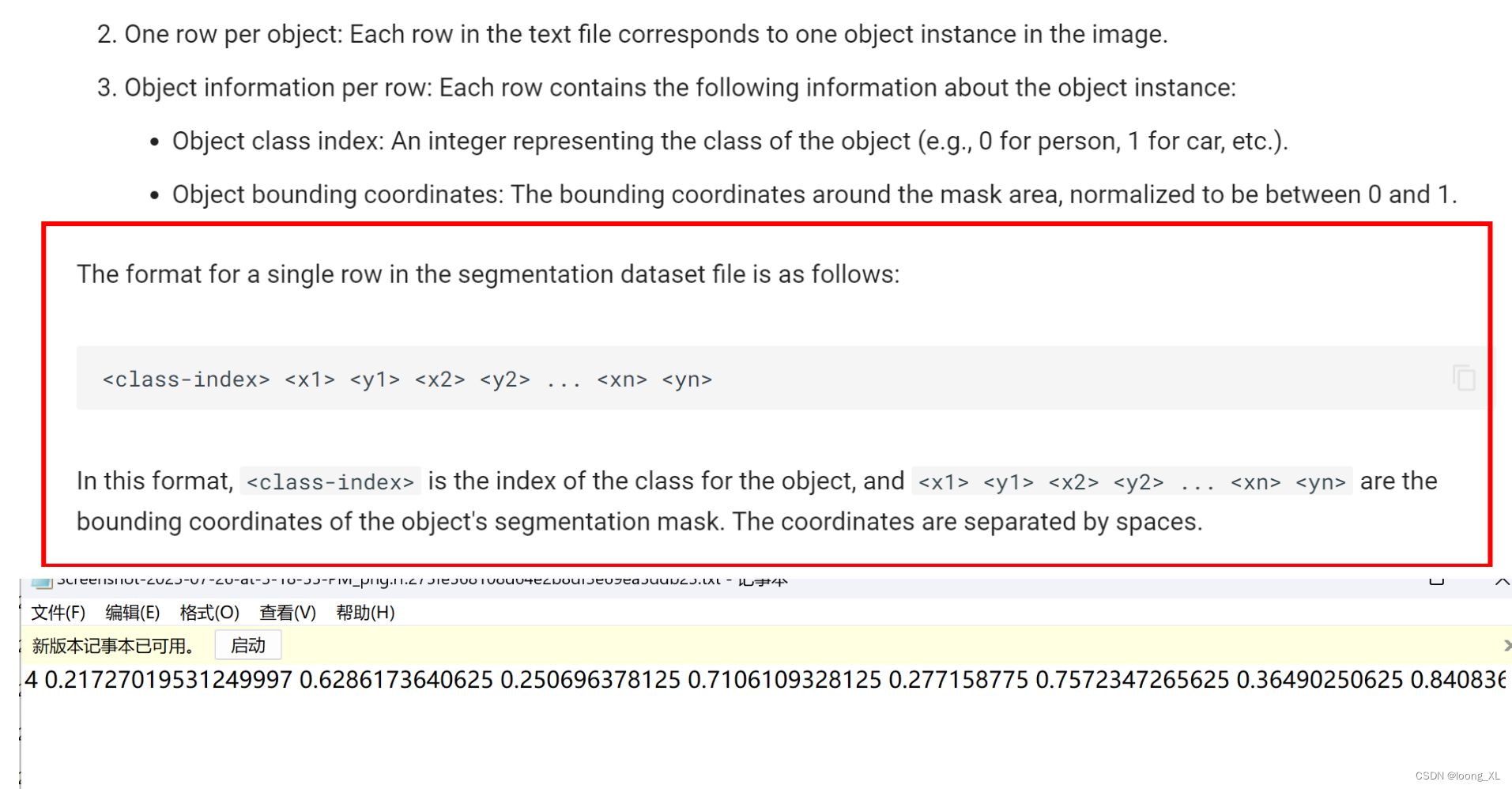
yolo 分割label格式标注信息图片显示可视化查看
参考: https://github.com/ultralytics/ultralytics/issues/3137 https://blog.csdn.net/weixin_42357472/article/details/135218349?spm=1001.2014.3001.5501 需要把坐标信息在图片上显示 代码 1)只画出了坐标边缘 import cv2 import numpy as np from random impor…...
霍兰德职业兴趣测试 60题(免费版)
霍兰德职业兴趣理论从兴趣的角度出发探索职业指导的问题,明确了职业兴趣的人格观念,使得人们对于职业兴趣的认识有了质的变化。在霍兰德职业兴趣理论提出来之前,职业兴趣和职业环境二者分别独立存在,正是霍兰德的总结,…...

MySQL之视图内连接、外连接、子查询
目录 一、视图 1.1 含义 2.1 视图的基本语法 二、案例 三、思维导图 一、视图 1.1 含义 虚拟表,和普通表一样使用 视图(view)是一个虚拟表,其内容由查询定义。同真实的表一样,视图包含一系列带有名称的列和行数据…...
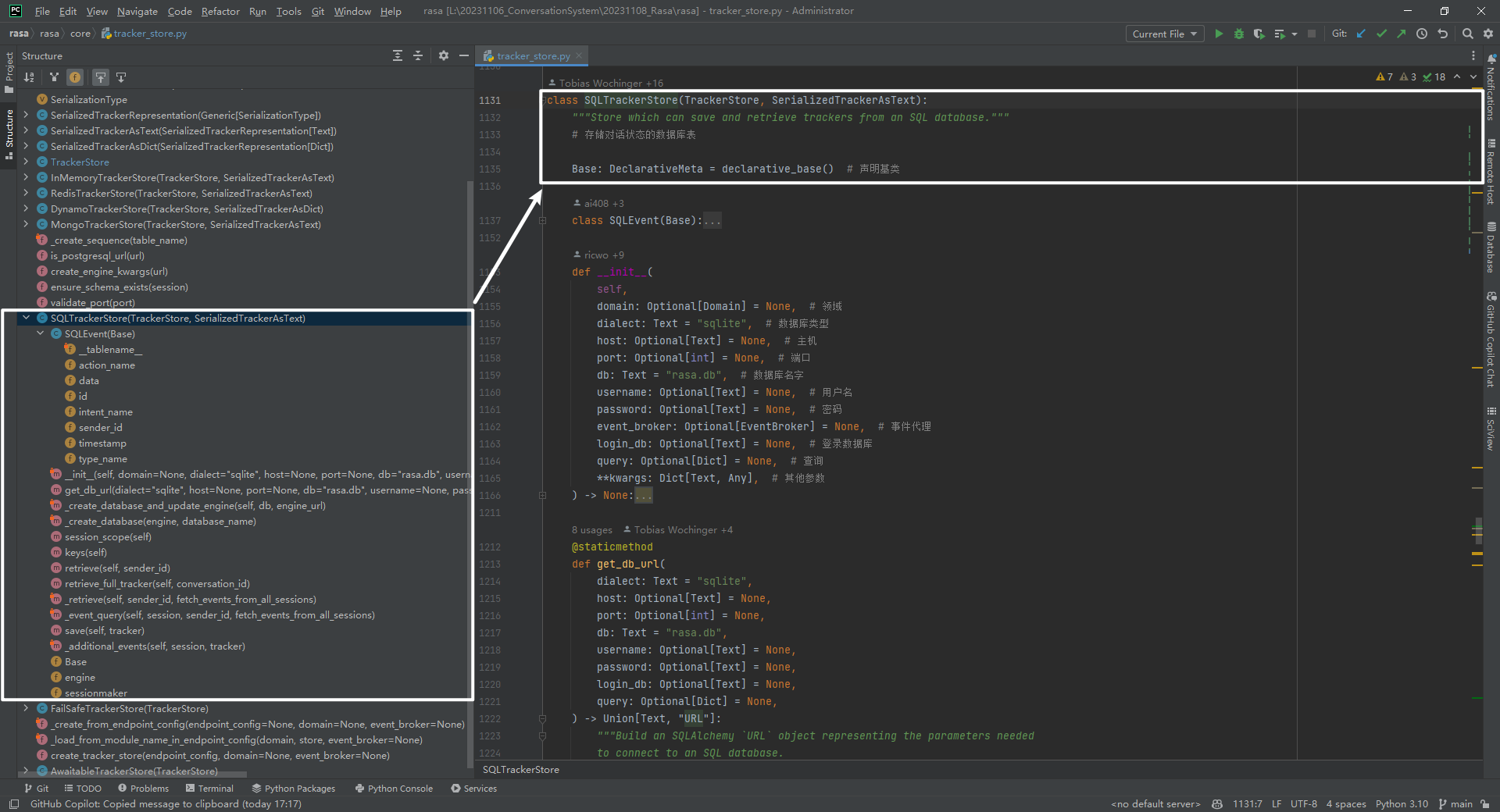
以报时机器人为例详细介绍tracker_store和event_broker
报时机器人源码参考[1][2],本文重点介绍当 tracker_store 类型为 SQL 时,events 表的表结构以及数据是如何生成的。以及当 event_broker 类型为 SQL 时,events 表的表结构以及数据是如何生成的。 一.报时机器人启动 [3] Rasa 对话系统启动方…...

理解JavaScript事件循环机制
JavaScript作为前端开发的核心语言之一,其事件循环机制是实现异步编程的关键。本文将深入探讨JavaScript事件循环机制,帮助您更好地理解它是如何工作的,以及如何在前端开发中充分利用这一机制。 1. 什么是事件循环? JavaScript是…...

自定义View之重写onMeasure
一、重写onMeasure()来修改已有的View的尺寸 步骤: 重写 onMeasure(),并调用 super.onMeasure() 触发原先的测量用 getMeasuredWidth() 和 getMeasuredHeight() 取到之前测得的尺寸,利用这两个尺寸来计算出最终尺寸使用 setMeasuredDimensio…...

专为Mac用户设计的思维导图软件MindNode 2023 for Mac助您激发创意!
在现代快节奏的生活中,我们经常需要整理思绪、规划项目、记录灵感。而思维导图作为一种高效的思维工具,能够帮助我们更好地整理和展现思维。现在,我们介绍一款强大而直观的思维导图软件——MindNode 2023 for Mac,助您拓展思维边界…...

Linux命令——用户和权限相关
文章目录 1 用户管理1.1 用户标识符1.2 用户添加1.3 用户删除1.4 用户配置文件1.4.1 passwd文件1.4.2 shadow文件1.4.3 group文件 2 密码管理3 权限管理 1 用户管理 1.1 用户标识符 用户标识符主要是UID和GID,UID表示用户id,GID表示用户组id。在登录的…...
linux反汇编工具: ida pro、rizinorg/cutter; ubuntu 22 flameshot延迟截图 以应对下拉菜单
rizinorg/cutter rizinorg/cutter 是 命令行反汇编工具 rizinorg/rizin 的图形化界面, 这比 ida pro跑在kvm虚拟机中方便多了, ubuntu22.04下直接下载Cutter-v2.3.2-Linux-x86_64.AppImage后即可运行,如下图: 注意 有个同名的报废品: radare2/Cutter 即 radare2的图形化界…...
】使用NiosV/m 处理器,niosv-download 为什么会失败?)
【INTEL(ALTERA)】使用NiosV/m 处理器,niosv-download 为什么会失败?
说明 在英特尔 Quartus Prime Pro Edition 软件 23.3 版及更高版本中将 Nios V 处理器软件下载到非流水线Nios V/m 处理器时,可能会出现此问题。 这是由于处理器限制,仅影响非流水线Nios V/m 处理器。 以下其他处理器不受此限制的影响: 管道…...
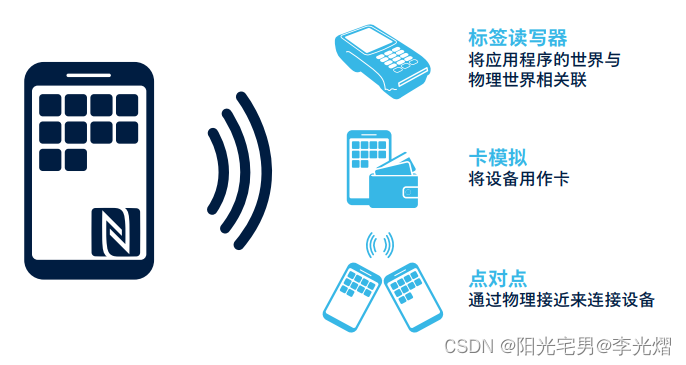
【无线通信专题】NFC通信模式及可能的应用方式
在文章【无线通信专题】NFC基本原理中我们讲到了NFC工作模式。其中NFC工作模式主要有三种,读写模式、卡模拟模式、点对点模式。 NFC通信模式丰富,NFC Forum定义了三种NFC设备:通用NFCForum设备、读写器设备和标签设备。这些NFC设备可以在三种通信模式下运行,并对应用案例进…...
pyinstaller生成的exe文件启动时间漫长的原因
加-F慢的原因是,pyinstaller把所有资源文件包括python解释器的依赖文件和库都打包到exe一个文件中,用户打开时,pyinstaller需要先执行一边解压操作,把依赖文件全部解压出来。慢就慢在这里。 如果不加-F,你会发现那些文…...

C语言基本语句介绍
c程序的执行部分是由语句组成的。程序的功能也是由执行语句来实现的,c语句分为6类 1表达式语句 表达式语句由表达式加上分号“;”组成 一般形式:表达式; 2函数调用语句 由函数名,实际参数加上分号“;”…...

【QT】QString类型中,Empty和NULL有什么区别在qt里,对比C#
在 Qt 中,QString 类型的字符串使用 isEmpty() 方法来检查字符串是否为空,而不是使用 null。这与 C# 中的 string.IsNullOrEmpty 方法略有不同。 QString::isEmpty(): 用于检查字符串是否为空。一个 QString 对象可能是空字符串,即…...

破壳而出:运维工程师在新科技热潮下的崛起与转型
运维工程师的出路到底在哪里? 在这个飞速发展的数字世界里,运维工程师无疑是IT界冲在最前线的勇士。他们曾是服务器的守护者,他们曾是故障的消灭者,他们曾是性能的推手。然而,随着科技的发展和市场需求的变化…...

多云管理“拦路虎”:深入解析网络互联、身份同步与成本可视化的技术复杂度
一、引言:多云环境的技术复杂性本质 企业采用多云策略已从技术选型升维至生存刚需。当业务系统分散部署在多个云平台时,基础设施的技术债呈现指数级积累。网络连接、身份认证、成本管理这三大核心挑战相互嵌套:跨云网络构建数据…...

Docker 离线安装指南
参考文章 1、确认操作系统类型及内核版本 Docker依赖于Linux内核的一些特性,不同版本的Docker对内核版本有不同要求。例如,Docker 17.06及之后的版本通常需要Linux内核3.10及以上版本,Docker17.09及更高版本对应Linux内核4.9.x及更高版本。…...

(二)原型模式
原型的功能是将一个已经存在的对象作为源目标,其余对象都是通过这个源目标创建。发挥复制的作用就是原型模式的核心思想。 一、源型模式的定义 原型模式是指第二次创建对象可以通过复制已经存在的原型对象来实现,忽略对象创建过程中的其它细节。 📌 核心特点: 避免重复初…...

2021-03-15 iview一些问题
1.iview 在使用tree组件时,发现没有set类的方法,只有get,那么要改变tree值,只能遍历treeData,递归修改treeData的checked,发现无法更改,原因在于check模式下,子元素的勾选状态跟父节…...
:滤镜命令)
ffmpeg(四):滤镜命令
FFmpeg 的滤镜命令是用于音视频处理中的强大工具,可以完成剪裁、缩放、加水印、调色、合成、旋转、模糊、叠加字幕等复杂的操作。其核心语法格式一般如下: ffmpeg -i input.mp4 -vf "滤镜参数" output.mp4或者带音频滤镜: ffmpeg…...

新能源汽车智慧充电桩管理方案:新能源充电桩散热问题及消防安全监管方案
随着新能源汽车的快速普及,充电桩作为核心配套设施,其安全性与可靠性备受关注。然而,在高温、高负荷运行环境下,充电桩的散热问题与消防安全隐患日益凸显,成为制约行业发展的关键瓶颈。 如何通过智慧化管理手段优化散…...

【Java_EE】Spring MVC
目录 Spring Web MVC 编辑注解 RestController RequestMapping RequestParam RequestParam RequestBody PathVariable RequestPart 参数传递 注意事项 编辑参数重命名 RequestParam 编辑编辑传递集合 RequestParam 传递JSON数据 编辑RequestBody …...

AI编程--插件对比分析:CodeRider、GitHub Copilot及其他
AI编程插件对比分析:CodeRider、GitHub Copilot及其他 随着人工智能技术的快速发展,AI编程插件已成为提升开发者生产力的重要工具。CodeRider和GitHub Copilot作为市场上的领先者,分别以其独特的特性和生态系统吸引了大量开发者。本文将从功…...

Python基于历史模拟方法实现投资组合风险管理的VaR与ES模型项目实战
说明:这是一个机器学习实战项目(附带数据代码文档),如需数据代码文档可以直接到文章最后关注获取。 1.项目背景 在金融市场日益复杂和波动加剧的背景下,风险管理成为金融机构和个人投资者关注的核心议题之一。VaR&…...

通过MicroSip配置自己的freeswitch服务器进行调试记录
之前用docker安装的freeswitch的,启动是正常的, 但用下面的Microsip连接不上 主要原因有可能一下几个 1、通过下面命令可以看 [rootlocalhost default]# docker exec -it freeswitch fs_cli -x "sofia status profile internal"Name …...
