Java学习苦旅(二十五)——哈希表
本篇博客将详细讲解哈希表。
文章目录
- 哈希表
- 概念
- 冲突
- 概念
- 避免冲突
- 哈希函数设计
- 常见哈希函数
- 负载因子调节
- 解决冲突
- 闭散列
- 开散列(哈希桶)
- 和java类集的关系
- 结尾
哈希表
概念
顺序结构以及平衡树中,元素关键码与其存储位置之间没有对应的关系,因此在查找一个元素时,必须要经过关键码的多次比较。顺序查找时间复杂度为O(N),平衡树中为树的高度,即O(log(N)),搜索的效率取决于搜索过程中元素的比较次数。
理想的搜索方法:可以不经过任何比较,一次直接从表中得到要搜索的元素。 如果构造一种存储结构,通过某种函数(hashFunc)使元素的存储位置与它的关键码之间能够建立一一映射的关系,那么在查找时通过该函数可以很快找到该元素。
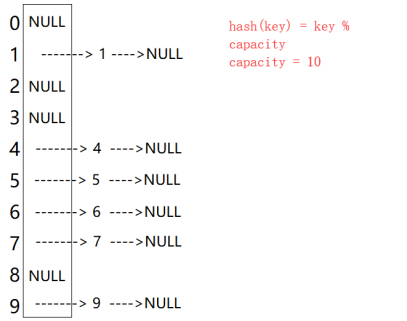
当向该结构中插入元素时,根据待插入元素的关键码,以此函数计算出该元素的存储位置并按此位置进行存放。当在该结构中搜索元素时,对元素的关键码进行同样的计算,把求得的函数值当做元素的存储位置,在结构中按此位置取元素比较,若关键码相等,则搜索成功。该方式即为哈希(散列)方法,哈希方法中使用的转换函数称为哈希(散列)函数,构造出来的结构称为哈希表(HashTable)(或者称散列表)。例如:
数据集合{1,7,6,4,5,9};
哈希函数设置为:hash(key) = key % capacity; capacity为存储元素底层空间总的大小。
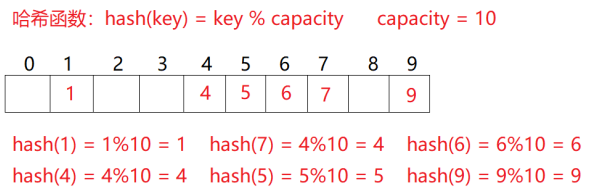
冲突
概念
对于两个数据元素的关键字ki和kj(i != j),有ki != kj,但有:Hash(ki) == Hash(kj),即:不同关键字通过相同哈希哈数计算出相同的哈希地址,该种现象称为哈希冲突或哈希碰撞。把具有不同关键码而具有相同哈希地址的数据元素称为“同义词”。
避免冲突
首先,我们需要明确一点,由于我们哈希表底层数组的容量往往是小于实际要存储的关键字的数量的,这就导致一个问题,冲突的发生是必然的,但我们能做的应该是尽量的降低冲突率。
哈希函数设计
引起哈希冲突的一个原因可能是:哈希函数设计不够合理。 哈希函数设计原则:
-
哈希函数的定义域必须包括需要存储的全部关键码,而如果散列表允许有m个地址时,其值域必须在0到m-1之间。
-
哈希函数计算出来的地址能均匀分布在整个空间中。
-
哈希函数应该比较简单
常见哈希函数
- 直接定制法
取关键字的某个线性函数为散列地址:Hash(Key)= A*Key + B。优点:简单、均匀。缺点:需要事先知道关键字的分布情况 使用场景:适合查找比较小且连续的情况。
- 除留余数法
设散列表中允许的地址数为m,取一个不大于m,但最接近或者等于m的质数p作为除数,按照哈希函数:Hash(key) = key% p(p<=m),将关键码转换成哈希地址。
- 平方取中法
假设关键字为1234,对它平方就是1522756,抽取中间的3位227作为哈希地址; 再比如关键字为4321,对它平方就是18671041,抽取中间的3位671(或710)作为哈希地址。
平方取中法比较适合:不知道关键字的分布,而位数又不是很大的情况。
- 折叠法
折叠法是将关键字从左到右分割成位数相等的几部分(最后一部分位数可以短些),然后将这几部分叠加求和,并按散列表表长,取后几位作为散列地址。
折叠法适合事先不需要知道关键字的分布,适合关键字位数比较多的情况。
- 随机数法
选择一个随机函数,取关键字的随机函数值为它的哈希地址,即H(key) = random(key),其中random为随机数函数。
通常应用于关键字长度不等时采用此法。
- 数学分析法
设有n个d位数,每一位可能有r种不同的符号,这r种不同的符号在各位上出现的频率不一定相同,可能在某些位上分布比较均匀,每种符号出现的机会均等,在某些位上分布不均匀只有某几种符号经常出现。可根据散列表的大小,选择其中各种符号分布均匀的若干位作为散列地址。
数字分析法通常适合处理关键字位数比较大的情况,如果事先知道关键字的分布且关键字的若干位分布较均匀的情况。
注意:哈希函数设计的越精妙,产生哈希冲突的可能性就越低,但是无法避免哈希冲突。
负载因子调节

负载因子和冲突率的关系粗略演示
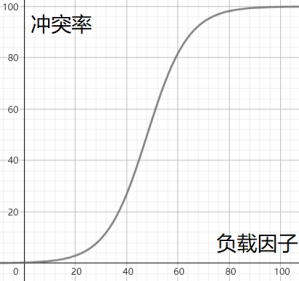
所以当冲突率达到一个无法忍受的程度时,我们需要通过降低负载因子来变相的降低冲突率。
已知哈希表中已有的关键字个数是不可变的,那我们能调整的就只有哈希表中的数组的大小。
解决冲突
解决哈希冲突两种常见的方法是:闭散列和开散列。
闭散列
闭散列:也叫开放定址法,当发生哈希冲突时,如果哈希表未被装满,说明在哈希表中必然还有空位置,那么可以把key存放到冲突位置中的“下一个”空位置中去。
寻找下一个位置的方法:
- 线性探测
比如上面的场景,现在需要插入元素44,先通过哈希函数计算哈希地址,下标为4,因此44理论上应该插在该位置,但是该位置已经放了值为4的元素,即发生哈希冲突。
线性探测:从发生冲突的位置开始,依次向后探测,直到寻找到下一个空位置为止。
插入
通过哈希函数获取待插入元素在哈希表中的位置。
如果该位置中没有元素则直接插入新元素,如果该位置中有元素发生哈希冲突,使用线性探测找到下一个空位置,插入新元素。
采用闭散列处理哈希冲突时,不能随便物理删除哈希表中已有的元素,若直接删除元素会影响其他元素的搜索。比如删除元素4,如果直接删除掉,44查找起来可能会受影响。因此线性探测采用标记的伪删除法来删除一个元素。
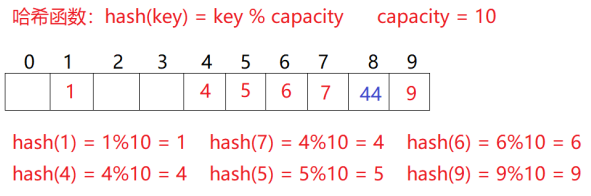
- 二次探测
线性探测的缺陷是产生冲突的数据堆积在一块,这与其找下一个空位置有关系,因为找空位置的方式就是挨着往后逐个去找,因此二次探测为了避免该问题,找下一个空位置的方法为:Hi= (H0+i2)% m,或者:Hi= (H0-i2)% m。其中:i = 1,2,3…,H0是通过散列函数Hash(x)对元素的关键码 key 进行计算得到的位置,m是表的大小。 对于如果要插入44,产生冲突,使用解决后的情况为:
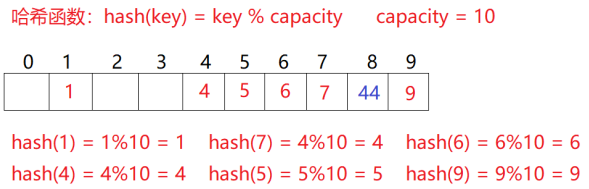
研究表明:当表的长度为质数且表装载因子a不超过0.5时,新的表项一定能够插入,而且任何一个位置都不会被探查两次。因此只要表中有一半的空位置,就不会存在表满的问题。在搜索时可以不考虑表装满的情况,但在插入时必须确保表的装载因子a不超过0.5,如果超出必须考虑增容。
因此:比散列最大的缺陷就是空间利用率比较低,这也是哈希的缺陷。
此外,从JDK1.8开始,当链表长度超过8,数组长度超过64,这个链表就会变成红黑树。
开散列(哈希桶)
开散列法又叫链地址法(开链法),首先对关键码集合用散列函数计算散列地址,具有相同地址的关键码归于同一子集合,每一个子集合称为一个桶,各个桶中的元素通过一个单链表链接起来,各链表的头结点存储在哈希表中。
从上图可以看出,开散列中每个桶中放的都是发生哈希冲突的元素。
开散列,可以认为是把一个在大集合中的搜索问题转化为在小集合中做搜索了。
示例代码
public class HashBuck {static class Node {public int key;public int val;public Node next;public Node(int key, int val) {this.key = key;this.val = val;}}public Node[] array;public int usedSize;public static final double DEFAULT_LOAD_FACTOR = 0.75;public HashBuck() {this.array = new Node[10];}public void put(int key, int val) {//找到key所在位置int index = key % this.array.length;//遍历这个下标的链表,看是否有相同的key,如果有,则需更新valueNode cur = array[index];while (cur != null) {if (cur.key == key) {cur.val = val;return;}cur = cur.next;}//没有这个key这个元素,头插法Node node = new Node(key,val);node.next = array[index];array[index] = node;this.usedSize++;//插入元素之后,检查当前列表的负载因子if (loadFactor() >= DEFAULT_LOAD_FACTOR) {resize();}}private void resize() {Node[] newArray = new Node[2*array.length];for (int i = 0; i < array.length; i++) {Node cur = array[i];while (cur != null) {int index = cur.key % newArray.length;//获取新的下标//将cur节点以头插或者尾插插入新的数组对应下标的链表中Node curNext = cur.next;cur.next = newArray[index];newArray[index] = cur;cur = curNext;}}array = newArray;}private double loadFactor() {return 1.0*usedSize/array.length;}/*** 根据key得到value* @param key* @return*/public int get(int key) {int index = key % this.array.length;Node cur = array[index];while (cur != null) {if (cur.key == key) {return cur.val;}}return -1;}
}
虽然哈希表一直在和冲突做斗争,但在实际使用过程中,我们认为哈希表的冲突率是不高的,冲突个数是可控的,也就是每个桶中的链表的长度是一个常数,所以,通常意义下,我们认为哈希表的插入/删除/查找时间复杂度是O(1) 。
和java类集的关系
-
HashMap 和 HashSet 即 java 中利用哈希表实现的 Map 和 Set。
-
java 中使用的是哈希桶方式解决冲突的。
-
java 会在冲突链表长度大于一定阈值后,将链表转变为搜索树(红黑树)。
-
java 中计算哈希值实际上是调用的类的 hashCode 方法,进行 key 的相等性比较是调用 key 的 equals 方法。所以如果要用自定义类作为 HashMap 的 key 或者 HashSet 的值,必须覆写hashCode和equals方法,而且要做到 equals 相等的对象,hashCode 一定是一致的。
结尾
本篇博客到此结束。
上一篇博客:Java学习苦旅(二十四)——Java中的内部类
下一篇博客:Java学习苦旅(二十六)——反射,枚举和lamda表达式
相关文章:

Java学习苦旅(二十五)——哈希表
本篇博客将详细讲解哈希表。 文章目录 哈希表概念冲突概念避免冲突哈希函数设计常见哈希函数 负载因子调节解决冲突闭散列开散列(哈希桶) 和java类集的关系 结尾 哈希表 概念 顺序结构以及平衡树中,元素关键码与其存储位置之间没有对应的关…...
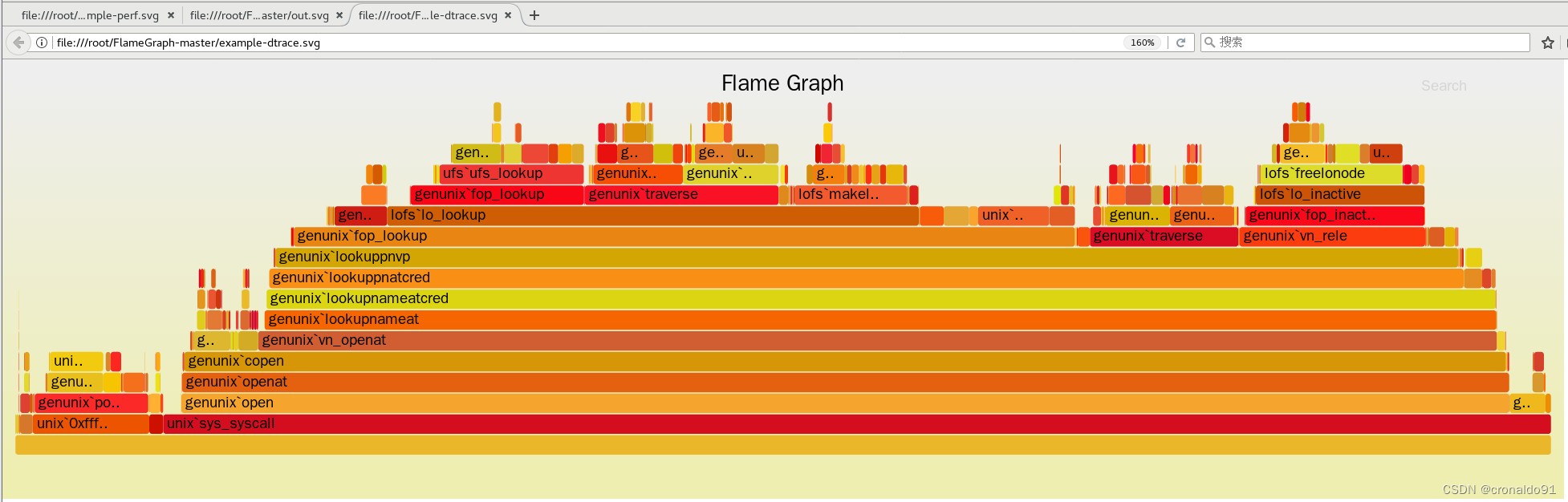
性能分析与调优: Linux 实现 CPU剖析与火焰图
目录 一、实验 1.环境 2.CPU 剖析 3.CPU火焰图 一、实验 1.环境 (1)主机 表1-1 主机 主机架构组件IP备注prometheus 监测 系统 prometheus、node_exporter 192.168.204.18grafana监测GUIgrafana192.168.204.19agent 监测 主机 node_exporter192…...
leetcode动态规划问题总结 Python
目录 一、基础理论 二、例题 1. 青蛙跳台阶 2. 解密数字 3. 最长不含重复字符的子字符串 4. 连续子数组的最大和 5. 最长递增子序列 6. 最长回文字符串 7. 机器人路径条数 8. 礼物的最大价值 一、基础理论 动态规划其实是一种空间换时间的基于历史数据的递推算法&…...

strtok函数的介绍
_str指被分解的字符串 delim指分隔符字符串 返回类型是指针 strtok()用来将字符串分割成一个个片段。参数s指向欲分割的字符串,参数delim则为分割字符串中包含的所有字符。当strtok()在参数s的字符串中发现参数delim中包含的分割字符时,则会将该字符改为\0 字符…...

CF1909_C. Heavy Intervals题解
CF1909_C. Heavy Intervals题解 题目传送门(Problem - C - CodeforcesCodeforces. Programming competitions and contests, programming communityhttps://codeforces.com/contest/1909/problem/C)。 题目翻译如下:(图片来源&a…...

【Python机器学习】理论知识:决策树
决策树是广泛用于分类和回归任务的模型,本质上是从一层层if/else问题中进行学习,并得出结论。这些问题类似于“是不是”中可能问到的问题。 决策树的每个结点代表一个问题或一个包含答案的终结点(叶结点)。树的边奖问题的答案与将…...
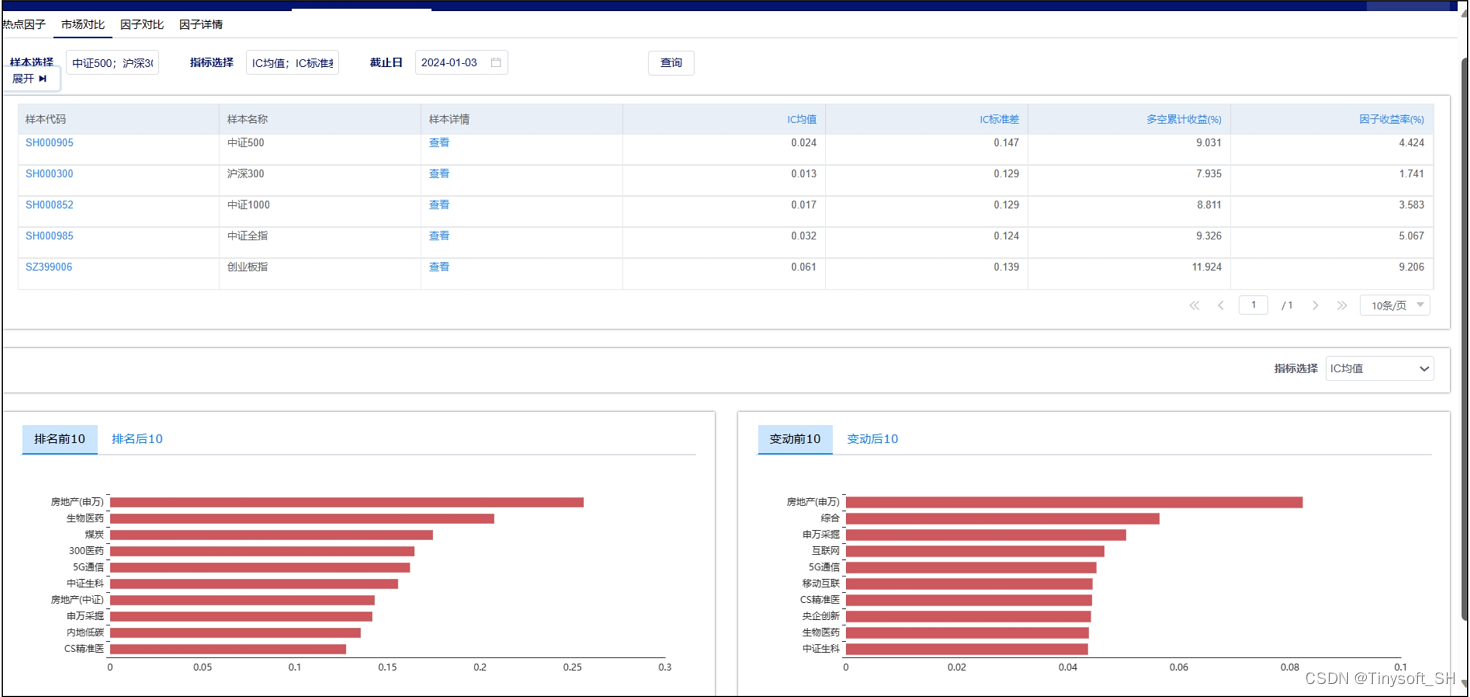
天软特色因子看板 (2024.01 第2期)
该因子看板跟踪天软特色因子A04001(当日趋势强度),该因子为反映股价走势趋势强弱,用以反映股价走势趋势强弱,abs(值)越接近1,趋势 性越强,符号代表涨跌方向 今日为该因子跟踪第2期,跟踪其在SH000905 (中证5…...
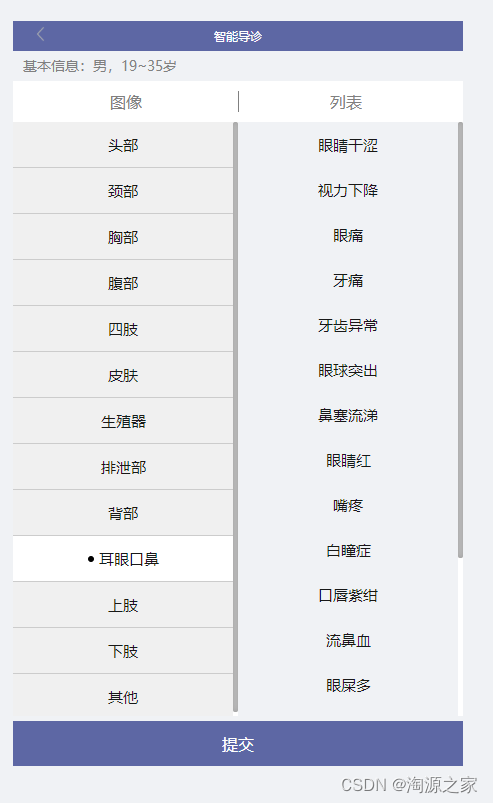
java智慧医院互联网智慧3D导诊系统源码,经由智慧导诊系统多维度计算,准确推荐科室
什么是智慧导诊系统? 简单地说,智慧导诊系统是一种利用人工智能技术,为医生提供帮助的系统。它可以通过分析患者的症状和病史为医生提供疾病诊断和治疗方案的建议。 系统介绍: 医院智慧导诊系统是在医院中使用的引导患者自助就诊挂号&…...

WiFi7: MLD寻址
原文:MLD使用MLD MAC address唯一的标识本MLD。 MLD下的STA(s)使用与之不同的MAC address。 NOTE MLD MAC address可以和其下的某个STA的MAC address相同或者不同于任一MAC Address。 原文:对于individually addressed 帧。以下规则适用: Address 2(TA)设置为STA的MAC Add…...
)
laravel-admin之 浏览器自动填充密码(如果需要渲染数据库密码的话,首先确认数据库密码是否可以逆向解密)
参考 https://blog.51cto.com/u_10401840/5180106 为什么浏览器端保存的密码一直自动写入到$form->password 解决办法 2、在页面进入的时候,默认表单的type值为text;推荐指数:2颗星 5、设置表单的readonly属性;推荐指数:4颗…...
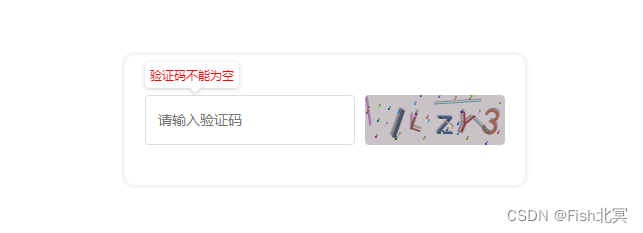
jquery图形验证码
效果展示 js图形随机验证码(表单验证) html代码片段 <form class"formwrap"><div class"item"><input type"text" id"code_input" value"" placeholder"请输入验证码"/>…...
dp专题10 目标和
本题链接:. - 力扣(LeetCode) 题目: 思路: 根据这道题,可以通过暴力的方法进行取 号或者 - 号 两个操作,通过当刚好得到 target 的时候 答案 1,但是通过长度是 20 ,操…...

详解 docker 镜像制作的两种方式
概要 制作Docker镜像一般有2种方法: 通过Dockerfile,完成镜像的创建使用仓库中已有的镜像,安装自己使用的软件环境后完成新镜像创建 docker 常用命令 docker build: 用于构建 Docker 镜像。该命令可以从 Dockerfile 构建镜像,…...

selenium元素单击不稳定解决方法
selenium自动化测试过程中,经常会发现某一元素单击,很不稳定,有时候执行了点击没有反映。 以下总结两种解决方法:都是通过js注入的方式去点击。 1.F12查一看,要点击的按钮,或连接,有没有οncl…...

vue3中vite使用sass
引用:https://blog.csdn.net/weiliang_66/article/details/132469597 npm install sass -d配置vite.config.js: css: {preprocessorOptions: {scss: {additionalData:import "/assets/styles/main.scss";}}}创建对应的 main.sass...

centos 8.0 安装sysbench 1.0.17
序号步骤说明执行命令执行结果备注1 下载并解压sysbench-1.0.17.zip sysbench-1.0.17.zip2安装依赖文件 yum install automake libtool -y yum install /usr/include/libpq-fe.h 3安装sysbench cd sysbench-1.0.17 ./autogen.sh ./configure \ --prefix/sysbench \ --with-pgsq…...
LabVIEW开发分布式光纤油气管道泄漏检测及预警系统
LabVIEW开发分布式光纤油气管道泄漏检测及预警系统 随着油气工业的发展,管道泄漏成为一个严峻的安全问题。本文介绍了一种基于LabVIEW的分布式光纤油气管道泄漏检测及预警系统的设计思路和组成结构。系统包括硬件和软件两部分,其中硬件部分详细阐述了分…...
Go后端开发 -- Go Modules
Go后端开发 – Go Modules 文章目录 Go后端开发 -- Go Modules一、什么是Go Modules?二、GOPATH的工作模式1.GOPATH模式2.GOPATH模式的弊端 三、Go Modules模式创建项目1.go mod命令2.go mod环境变量3.使用Go Modules初始化项目4.修改模块的版本依赖关系 四、Go Modules下impo…...
)
基于det_keypoint_unite的ROS功能包(jetson部署)
文章目录 硬件软件FastDeploy编译CMakeLists.txt头文件源代码硬件 Jetson AGX Orin 64GB 软件 gcc/g++ >= 5.4(推荐8.2)cmake >= 3.10.0jetpack >= 4.6.1opencv=4.2.0FastDeploy编译 git clone https://github.com/PaddlePaddle/FastDeploy.git cd FastDeploy mkdi…...

TS 36.211 V12.0.0-下行(8)-调制和上变频
本文的内容主要涉及TS 36.211,版本是C00,也就是V12.0.0。...

React第五十七节 Router中RouterProvider使用详解及注意事项
前言 在 React Router v6.4 中,RouterProvider 是一个核心组件,用于提供基于数据路由(data routers)的新型路由方案。 它替代了传统的 <BrowserRouter>,支持更强大的数据加载和操作功能(如 loader 和…...

【磁盘】每天掌握一个Linux命令 - iostat
目录 【磁盘】每天掌握一个Linux命令 - iostat工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景 注意事项 【磁盘】每天掌握一个Linux命令 - iostat 工具概述 iostat(I/O Statistics)是Linux系统下用于监视系统输入输出设备和CPU使…...

DIY|Mac 搭建 ESP-IDF 开发环境及编译小智 AI
前一阵子在百度 AI 开发者大会上,看到基于小智 AI DIY 玩具的演示,感觉有点意思,想着自己也来试试。 如果只是想烧录现成的固件,乐鑫官方除了提供了 Windows 版本的 Flash 下载工具 之外,还提供了基于网页版的 ESP LA…...

2025 后端自学UNIAPP【项目实战:旅游项目】6、我的收藏页面
代码框架视图 1、先添加一个获取收藏景点的列表请求 【在文件my_api.js文件中添加】 // 引入公共的请求封装 import http from ./my_http.js// 登录接口(适配服务端返回 Token) export const login async (code, avatar) > {const res await http…...

【AI学习】三、AI算法中的向量
在人工智能(AI)算法中,向量(Vector)是一种将现实世界中的数据(如图像、文本、音频等)转化为计算机可处理的数值型特征表示的工具。它是连接人类认知(如语义、视觉特征)与…...

vue3+vite项目中使用.env文件环境变量方法
vue3vite项目中使用.env文件环境变量方法 .env文件作用命名规则常用的配置项示例使用方法注意事项在vite.config.js文件中读取环境变量方法 .env文件作用 .env 文件用于定义环境变量,这些变量可以在项目中通过 import.meta.env 进行访问。Vite 会自动加载这些环境变…...

DeepSeek 技术赋能无人农场协同作业:用 AI 重构农田管理 “神经网”
目录 一、引言二、DeepSeek 技术大揭秘2.1 核心架构解析2.2 关键技术剖析 三、智能农业无人农场协同作业现状3.1 发展现状概述3.2 协同作业模式介绍 四、DeepSeek 的 “农场奇妙游”4.1 数据处理与分析4.2 作物生长监测与预测4.3 病虫害防治4.4 农机协同作业调度 五、实际案例大…...
)
Typeerror: cannot read properties of undefined (reading ‘XXX‘)
最近需要在离线机器上运行软件,所以得把软件用docker打包起来,大部分功能都没问题,出了一个奇怪的事情。同样的代码,在本机上用vscode可以运行起来,但是打包之后在docker里出现了问题。使用的是dialog组件,…...

Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习)
Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习) 一、Aspose.PDF 简介二、说明(⚠️仅供学习与研究使用)三、技术流程总览四、准备工作1. 下载 Jar 包2. Maven 项目依赖配置 五、字节码修改实现代码&#…...

Mysql中select查询语句的执行过程
目录 1、介绍 1.1、组件介绍 1.2、Sql执行顺序 2、执行流程 2.1. 连接与认证 2.2. 查询缓存 2.3. 语法解析(Parser) 2.4、执行sql 1. 预处理(Preprocessor) 2. 查询优化器(Optimizer) 3. 执行器…...
