【学习笔记】NOIP暴零赛2
细思极恐,我的能力已经退步到这个地步了吗?
数据结构
这题的修改是强行加进去迷惑你的。
考虑怎么求树的带权重心。
完了我只会树形dp
完了完了
结论:设uuu的子树和为szusz_uszu,所有点权值和为sss,那么树的带权重心等价于,满足szu≥⌈s2⌉sz_u\ge \lceil\frac{s}{2}\rceilszu≥⌈2s⌉且深度最大的点uuu。
似乎机房大部分人都想到了这一点,只有我是joker???
道理很简单。显然这个条件是必要的。其次,uuu肯定在根节点所在的重链上,并且满足条件的点一定是重链的一段前缀,容易发现只有这一段前缀的结尾那个点能作为树的重心。
下面的分析就很简单了。
第一种方法,我们只要能确定一个点一定在重心的子树内,然后从这个点往上跳即可。下一步比较构造,考虑在dfn\text{dfn}dfn序中找到第一个满足前缀和≥⌈s2⌉\ge \lceil\frac{s}{2}\rceil≥⌈2s⌉的点,这个点一定在重心的子树对应的那段dfn\text{dfn}dfn序上,换句话说一定在重心的子树内,往上跳即可。注意树的重心可能有两个,因此uuu的父亲也可能是重心,所以当子树和恰好是s2\frac{s}{2}2s时要返回uuu的父亲。又因为点权可能为零,因此最后要先跳一段000再返回父亲。
第二种方法,记录上一次重心的位置,如果是对链操作,那么新的重心一定在链端点的祖先上,如果是对子树操作,那么新的重心可能在uuu的祖先上,也可能在uuu的重链上,直接在重链上跳即可。
复杂度O(nlog2n)O(n\log^2 n)O(nlog2n)。
#include<bits/stdc++.h>
#define ll long long
#define pb push_back
#define inf 0x3f3f3f3f3f3f3f3f
using namespace std;
const int N=3e5+5;
int n,Q,f[N][20],dfn[N],dep[N],tp[N],sz[N],son[N],rk[N],num;
ll sum;
vector<int>g[N];
struct node{ll sum,dat;
}t[N<<2];
void add(int p,int l,int r,ll x){t[p].sum+=(r-l+1)*x,t[p].dat+=x;
}
void pushdown(int p,int l,int r){int mid=l+r>>1;if(t[p].dat){add(p<<1,l,mid,t[p].dat),add(p<<1|1,mid+1,r,t[p].dat),t[p].dat=0;}
}
void pushup(int p){t[p].sum=t[p<<1].sum+t[p<<1|1].sum;
}
void upd(int p,int l,int r,int ql,int qr,ll x){if(ql<=l&&r<=qr){add(p,l,r,x);return;}int mid=l+r>>1;pushdown(p,l,r);if(ql<=mid)upd(p<<1,l,mid,ql,qr,x);if(mid<qr)upd(p<<1|1,mid+1,r,ql,qr,x);pushup(p);
}
ll qry(int p,int l,int r,int ql,int qr){if(ql<=l&&r<=qr)return t[p].sum;int mid=l+r>>1;pushdown(p,l,r);if(qr<=mid)return qry(p<<1,l,mid,ql,qr);if(mid<ql)return qry(p<<1|1,mid+1,r,ql,qr);return qry(p<<1,l,mid,ql,qr)+qry(p<<1|1,mid+1,r,ql,qr);
}
void dfs(int u,int topf){sz[u]=1,f[u][0]=topf,dep[u]=dep[topf]+1;for(int i=1;i<20;i++)f[u][i]=f[f[u][i-1]][i-1];for(auto v:g[u]){if(v!=topf){dfs(v,u),sz[u]+=sz[v];if(sz[v]>sz[son[u]])son[u]=v;}}
}
void dfs2(int u,int topf){tp[u]=topf,dep[u]=dep[topf]+1,dfn[u]=++num,rk[num]=u;if(son[u])dfs2(son[u],topf);for(auto v:g[u]){if(!dfn[v])dfs2(v,v);}
}
int Lca(int x,int y){if(dep[x]<dep[y])swap(x,y);for(int i=19;i>=0;i--)if(dep[f[x][i]]>=dep[y])x=f[x][i];if(x==y)return x;for(int i=19;i>=0;i--)if(f[x][i]!=f[y][i])x=f[x][i],y=f[y][i];return f[x][0];
}
int query(){int l=1,r=n,res=0;sum=t[1].sum;while(l<=r){int mid=l+r>>1;if(qry(1,1,n,1,mid)>=(sum+1)/2)res=mid,r=mid-1;else l=mid+1;}res=rk[res];if(qry(1,1,n,dfn[res],dfn[res]+sz[res]-1)<(sum+1)/2){for(int i=19;i>=0;i--){int u=f[res][i];if(u&&qry(1,1,n,dfn[u],dfn[u]+sz[u]-1)<(sum+1)/2)res=u;}res=f[res][0];}if(qry(1,1,n,dfn[res],dfn[res]+sz[res]-1)==sum/2){for(int i=19;i>=0;i--){int u=f[res][i];if(u&&qry(1,1,n,dfn[u],dfn[u]+sz[u]-1)==sum/2)res=u;}if(f[res][0])return f[res][0];return res;}return res;
}
int main(){ios::sync_with_stdio(false);cin.tie(0),cout.tie(0);cin>>n;for(int i=1;i<n;i++){int u,v;cin>>u>>v,g[u].pb(v),g[v].pb(u);}cin>>Q;dfs(1,0),dfs2(1,1);for(int i=1;i<=Q;i++){int op,x,y,w;cin>>op>>x>>y;if(op==1){upd(1,1,n,dfn[x],dfn[x]+sz[x]-1,y);}else{cin>>w;int fx=tp[x],fy=tp[y];while(fx!=fy){if(dep[fx]>dep[fy])upd(1,1,n,dfn[fx],dfn[x],w),x=f[fx][0];else upd(1,1,n,dfn[fy],dfn[y],w),y=f[fy][0];fx=tp[x],fy=tp[y];}if(dfn[x]>dfn[y])swap(x,y);upd(1,1,n,dfn[x],dfn[y],w);}cout<<query()<<"\n";}
}
签到
吐槽:好好的题,为什么要强行套上高精度这样恶心的东西?单纯为了恶心选手吗?
把容斥的式子写出来:(−1)∣S∣(n+m−(c−1)∣S∣−∑i∈Sbim)(-1)^{|S|}\binom{n+m-(c-1)|S|-\sum_{i\in S}{b^i}}{m}(−1)∣S∣(mn+m−(c−1)∣S∣−∑i∈Sbi)
然而直接组合数非常难算。但是注意到mmm很小,因此我们可以把组合数看成一个多项式。
刚开始想的是一些比较特殊的情况,可以简单递推求出,但是发现对于普通的情况难以处理,感觉数位dpdpdp部分又比较麻烦于是就一无所获了。
首先把nnn转化成bbb进制,然后枚举∣S∣|S|∣S∣。为什么我想不到正解的思路呢 注意到∑i∈Sbi\sum_{i\in S}b^i∑i∈Sbi的数位上都是111,因此我们枚举一段前缀就不用考虑负数的情况。问题转化为,从1,2,...,m1,2,...,m1,2,...,m中选kkk个数,记作集合TTT,对于每个i∈[1,m]i\in [1,m]i∈[1,m],求每种情况下(∑j∈Tbj)i(\sum_{j\in T}b_j)^i(∑j∈Tbj)i的和。最简单的想法是,每次加入一个数时,用二项式定理暴力展开。这可以用O(n4)O(n^4)O(n4)的dpdpdp预处理求出。
总复杂度O(n4)O(n^4)O(n4)。一道将数位dpdpdp,容斥,多项式,高精度强行拼凑的辣鸡的毒瘤签到题
爆搜
不会。只会O(2npoly(n))O(2^n\text{poly}(n))O(2npoly(n))的做法。
似乎大家t2都挂分了,但是只有我t2是不会做,我好菜啊???
相关文章:

【学习笔记】NOIP暴零赛2
细思极恐,我的能力已经退步到这个地步了吗? 数据结构 这题的修改是强行加进去迷惑你的。 考虑怎么求树的带权重心。 完了我只会树形dp 完了完了 结论:设uuu的子树和为szusz_uszu,所有点权值和为sss,那么树的带…...

linux基本功系列之hostname实战
文章目录前言一. hostname命令介绍二. 语法格式及常用选项三. 参考案例3.1 显示本机的主机名3.2 临时修改主机名3.3 显示短格式的主机名3.4 显示主机的ip地址四. 永久修改主机名4.1 centos6 修改主机名的方式4.2 centos7中修改主机名永久生效总结前言 大家好,又见面…...
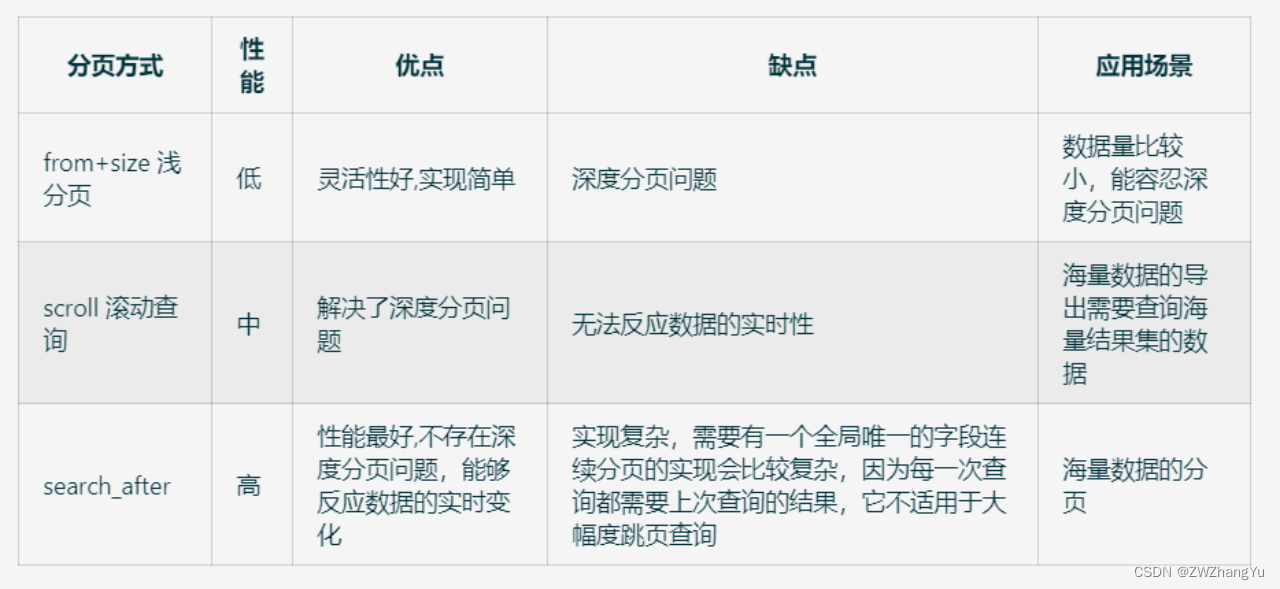
Easy-Es框架实践测试整理 基于ElasticSearch的ORM框架
文章目录介绍(1)Elasticsearch java 客户端种类(2)优势和特性分析(3)性能、安全、拓展、社区(2)ES版本及SpringBoot版本说明索引处理(一)索引别名策略&#x…...
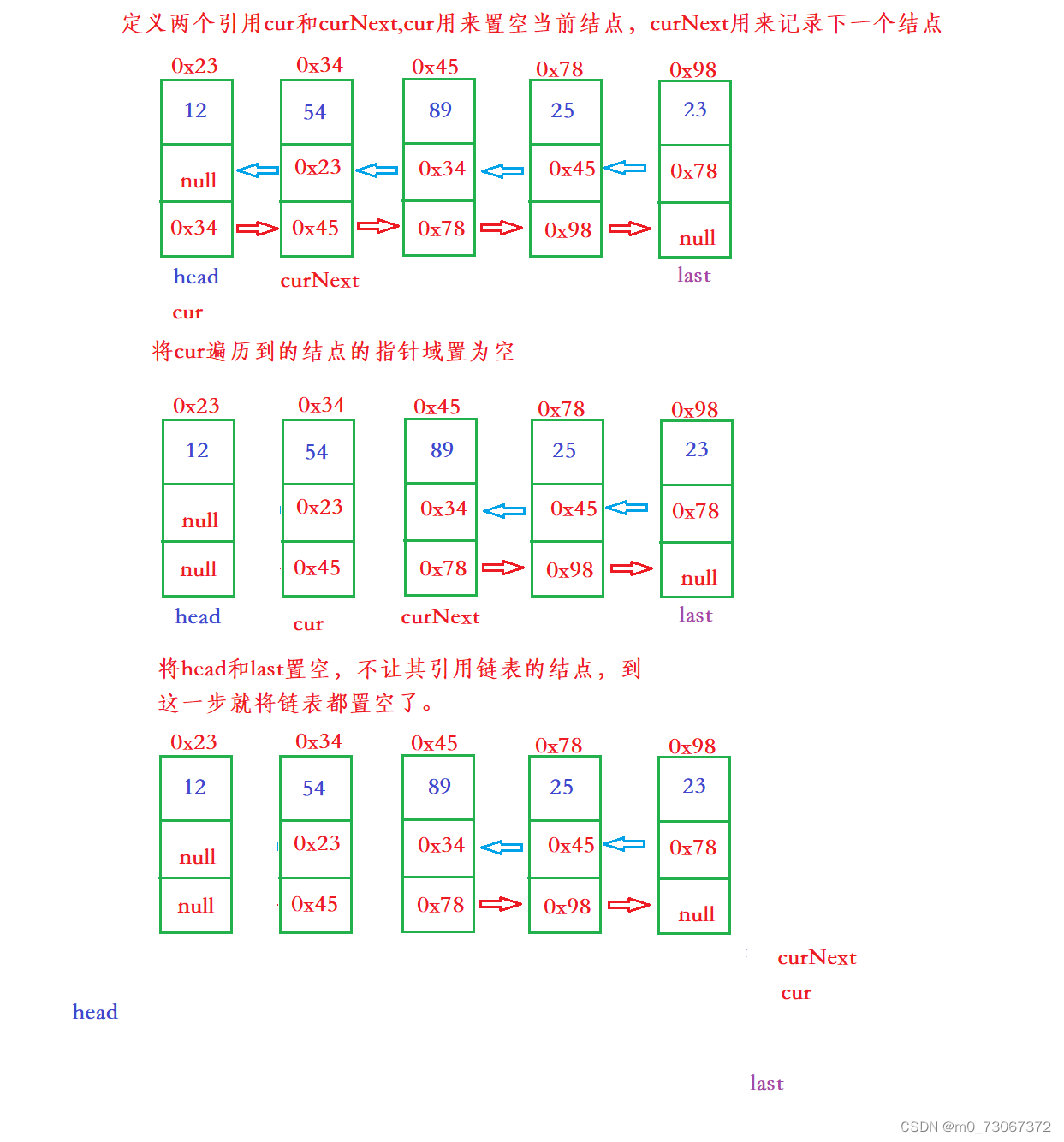
【数据结构】双向链表的模拟实现(无头)
目录 前言: 1、认识双向链表中的结点 2、认识并创建无头双向链表 3、实现双向链表当中的一些方法 3.1、遍历输出方法(display) 3.2、得到链表的长度(size) 3.3、查找关键字key是否包含在双链表中(contains) 3.…...

vue自定义指令---处理加载图片失败时出现的碎图,onerror事件
目录 一、自定义指令 1、局部注册和使用 2、全局注册和使用 二、自定义指令处理图片加载失败(碎图) 一、自定义指令 vue中除v-model、v-show等内置指令之外,还允许注册自定义指令,获取DOM元素,扩展额外的功能。 1、局…...

加盟管理系统挑选法则,看完不怕被坑!
经营服装连锁店铺究竟有多难?小编已经不止一次听到身边的老板,抱怨加盟连锁店铺难以管理了,但同时呢,也听到了很多作为加盟商的老板,抱怨总部给的支持和管理不到位。服装加盟店铺管理,到底有哪些难点呢&…...

alertmanager笔记
1 prometheus的思想 所有告警都应该立刻处理掉,不应该存在长时间未解决的告警。所以具体的表现就是高频的数据采集,和告警的自动恢复(默认5分钟) 2 alertmanager API调用 使用如下命令即可手工制造告警,注意startsA…...
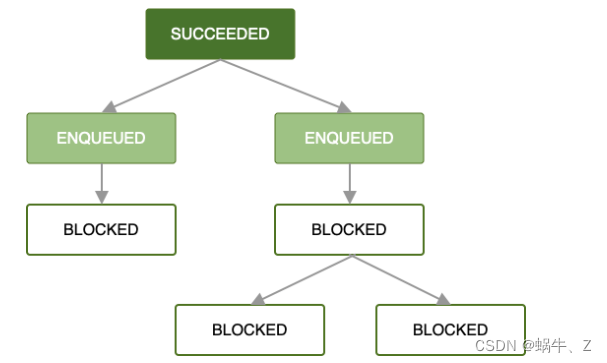
Android Jetpack组件之WorkManager后台任务管理的介绍与使用(二)
一、介绍 通过上一篇文,Android Jetpack组件之WorkManager后台任务管理的介绍与使用(一)_蜗牛、Z的博客-CSDN博客 我们可以弄清楚workmanager从接入到使用的基本流程。基本可以满足我们日常。那只是简单的入门。如果遇到更复杂的功能,那简单的就无法满…...

【MySQL】第十七部分 约束
【MySQL】第十七部分 约束 文章目录【MySQL】第十七部分 约束17. 约束17.1 约束的分类17.2 非空约束17.3 唯一性约束17.4 主键约束17.5 自增列约束17.6 外键约束17.7 默认约束17.8 check约束总结17. 约束 约束: 可以在创建表的时候规定约束,也可以在表创建之后添加,约束顾名思…...
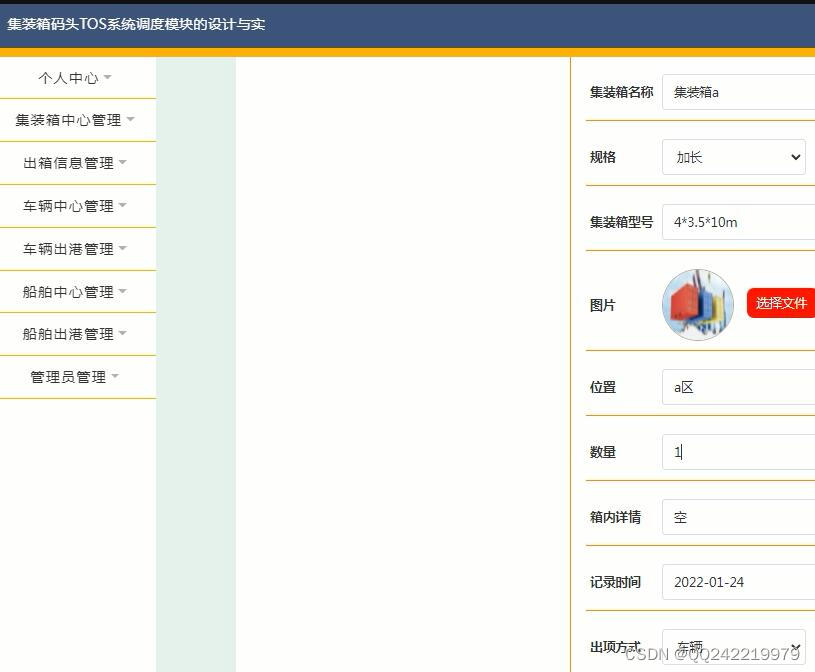
java ssm集装箱码头TOS系统调度模块的设计与实现
由于历史和经济体制的原因,国内码头物流企业依然保持大而全的经营模式。企业自己建码头、场地、经营集装箱运输车辆。不过近几年来随着经济改革的进一步深入和竞争的激烈,一些大型的码头物流企业逐步打破以前的经营模式,其中最明显的特征就是…...

MS14-064(OLE远程代码执行漏洞复现)
✅作者简介:CSDN内容合伙人、信息安全专业在校大学生🏆 🔥系列专栏 :内网安全-漏洞复现 📃新人博主 :欢迎点赞收藏关注,会回访! 💬舞台再大,你不上台…...

【C++深陷】之shared_ptr
0. 什么是智能指针 使用new 和delete 手动进行动态内存管理很容易出现内存泄漏等问题。C11为了更安全、更方便的管理动态内存,新的标准库提供了两种智能指针(smart pointer):shared_ptr和unique_ptr,以及一个伴随类we…...
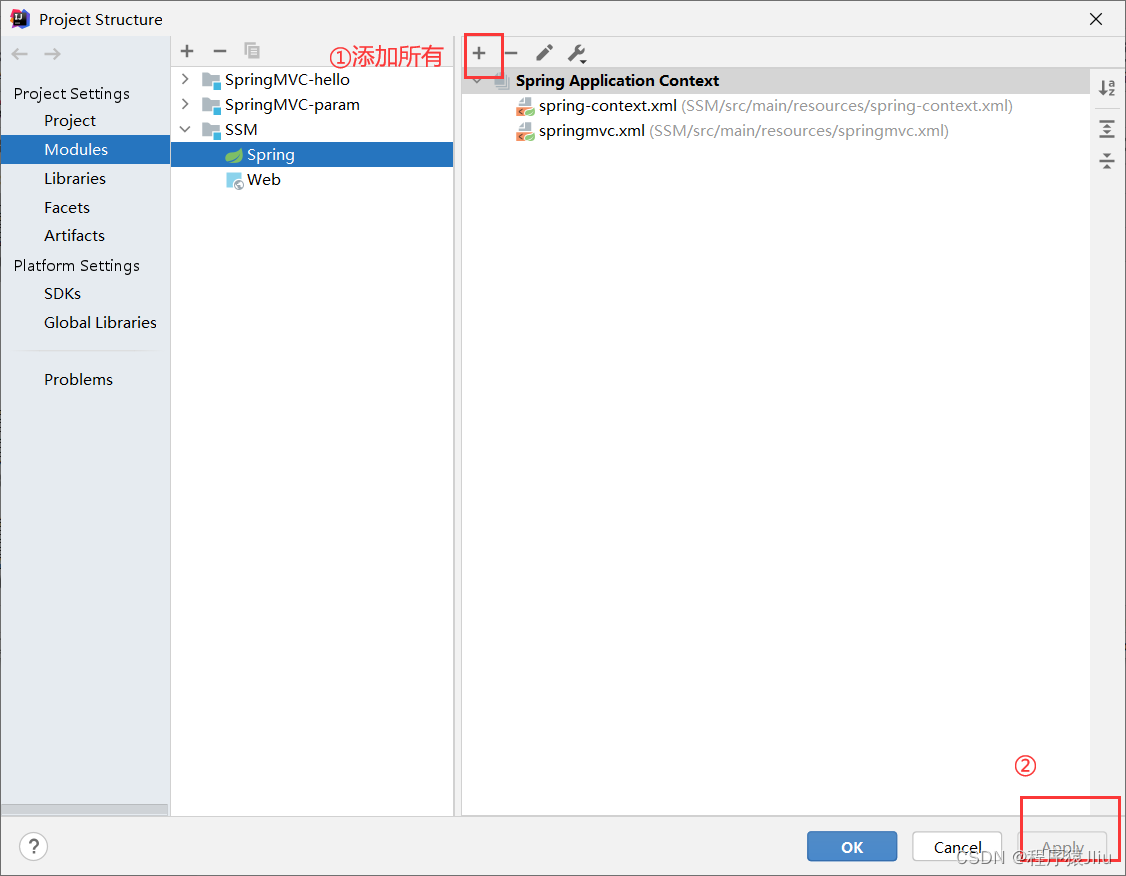
SpringMVC中遇到的错误
SpringMVC中遇到的错误1.web.xml中配置SpringMVC核心类: DispatcherServlet 报错解决方案:添加Tomcat包2. not declaration can be found for element--------‘mvc:annotation-driven‘通配符的匹配很全面, 但无法找到元素 mvc:annotation-driven 的声明解决方案&a…...

姿态估计端到端新方案 | DirectMHP:用于全范围角度2D多人头部姿势估计
前言 现有的头部姿势估计主要集中在具有预先检测到的正面头部的单个人,这依赖于单独训练的面部检测器,不能很好地泛化到完整的视点。在本文中,作者关注全范围 MPHPE 问题,并提出了一个名为 DirectMHP 的直接端到端简单基线&#x…...
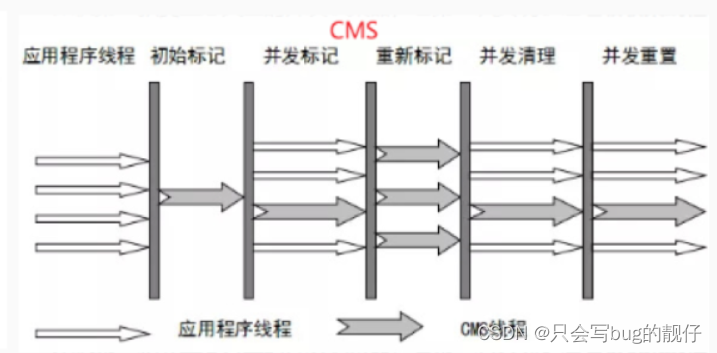
jvm学习的核心(五)---垃圾回收算法和常见垃圾回收器
文章目录1.垃圾回收算法**1.1. 标记阶段****1.2. 清除阶段**1.2.1.标记清除算法1.2.2.标记复制算法1.2.3.标记整理算法1.3.引用2.常见的垃圾回收器2.1.Serial回收器2.2.ParNew回收器2.3.Parallel回收器2.4.CMS回收器<font color red>2.5.G1垃圾回收器ZGC回收器ÿ…...

亿级高并发电商项目-- 实战篇 --万达商城项目 二(Zookeeper、Docker、Dubbo-Admin等搭建工作
👏作者简介:大家好,我是小童,Java开发工程师,CSDN博客博主,Java领域新星创作者 📕系列专栏:前端、Java、Java中间件大全、微信小程序、微信支付、若依框架、Spring全家桶 Ǵ…...

【C#基础】 C# 数据类型总结
序号系列文章0【C#基础】初识编程语言C#1【C#基础】C# 程序通用结构总结2【C#基础】C# 程序基础语法解析文章目录前言数据类型一. 值类型(Value types)二. 引用类型(Reference types)三. 指针类型(Pointer types&#…...

格子玻尔兹曼法介绍
1 LBM简介格子玻尔兹曼法(Lattice Boltzmann Method)简称LBM,是一种CFD算法,可求解流动、传热等常见CFD问题。LBM基于格子玻尔兹曼方程(LBE),从介观尺度(mesoscope)描述了…...
活动星投票在时间的河流上造园分组怎么设置如何进行分组报名
“在时间的河流上造园”网络评选投票_免费小程序运行系统_企业有关的投票_微信投票的应用小程序投票活动如何做?很多企业在运营当中,都会通过投票活动来进行推广,从而达到吸粉、增加用户粘度等效果。而此类投票活动,通过小程序就可…...

c#小笔记本-基础
c#基本知识一.基础操作1.打印-writeline,write2.输入-readline,readkey二.变量1.折叠代码-#region,#endregion2.变量类型(在c语言变量类型上新增的)三.常量-const四.转义字符五.显示转换1.括号强转-低精度装高精度2.parse法-作用于字符串3.co…...

日语AI面试高效通关秘籍:专业解读与青柚面试智能助攻
在如今就业市场竞争日益激烈的背景下,越来越多的求职者将目光投向了日本及中日双语岗位。但是,一场日语面试往往让许多人感到步履维艰。你是否也曾因为面试官抛出的“刁钻问题”而心生畏惧?面对生疏的日语交流环境,即便提前恶补了…...

C++ 基础特性深度解析
目录 引言 一、命名空间(namespace) C 中的命名空间 与 C 语言的对比 二、缺省参数 C 中的缺省参数 与 C 语言的对比 三、引用(reference) C 中的引用 与 C 语言的对比 四、inline(内联函数…...

linux 下常用变更-8
1、删除普通用户 查询用户初始UID和GIDls -l /home/ ###家目录中查看UID cat /etc/group ###此文件查看GID删除用户1.编辑文件 /etc/passwd 找到对应的行,YW343:x:0:0::/home/YW343:/bin/bash 2.将标红的位置修改为用户对应初始UID和GID: YW3…...

leetcodeSQL解题:3564. 季节性销售分析
leetcodeSQL解题:3564. 季节性销售分析 题目: 表:sales ---------------------- | Column Name | Type | ---------------------- | sale_id | int | | product_id | int | | sale_date | date | | quantity | int | | price | decimal | -…...

Linux --进程控制
本文从以下五个方面来初步认识进程控制: 目录 进程创建 进程终止 进程等待 进程替换 模拟实现一个微型shell 进程创建 在Linux系统中我们可以在一个进程使用系统调用fork()来创建子进程,创建出来的进程就是子进程,原来的进程为父进程。…...

管理学院权限管理系统开发总结
文章目录 🎓 管理学院权限管理系统开发总结 - 现代化Web应用实践之路📝 项目概述🏗️ 技术架构设计后端技术栈前端技术栈 💡 核心功能特性1. 用户管理模块2. 权限管理系统3. 统计报表功能4. 用户体验优化 🗄️ 数据库设…...

Java求职者面试指南:计算机基础与源码原理深度解析
Java求职者面试指南:计算机基础与源码原理深度解析 第一轮提问:基础概念问题 1. 请解释什么是进程和线程的区别? 面试官:进程是程序的一次执行过程,是系统进行资源分配和调度的基本单位;而线程是进程中的…...

uniapp手机号一键登录保姆级教程(包含前端和后端)
目录 前置条件创建uniapp项目并关联uniClound云空间开启一键登录模块并开通一键登录服务编写云函数并上传部署获取手机号流程(第一种) 前端直接调用云函数获取手机号(第三种)后台调用云函数获取手机号 错误码常见问题 前置条件 手机安装有sim卡手机开启…...

C++ 设计模式 《小明的奶茶加料风波》
👨🎓 模式名称:装饰器模式(Decorator Pattern) 👦 小明最近上线了校园奶茶配送功能,业务火爆,大家都在加料: 有的同学要加波霸 🟤,有的要加椰果…...

高分辨率图像合成归一化流扩展
大家读完觉得有帮助记得关注和点赞!!! 1 摘要 我们提出了STARFlow,一种基于归一化流的可扩展生成模型,它在高分辨率图像合成方面取得了强大的性能。STARFlow的主要构建块是Transformer自回归流(TARFlow&am…...
