Android 8.1 隐藏设置中定位功能
Android 8.1 隐藏设置中定位功能
最近接到客户反馈,需要隐藏设备设置中的定位功能,具体修改参照如下:
/vendor/mediatek/proprietary/packages/apps/MtkSettings/src/com/android/settings/SecuritySettings.java
mLocationcontroller.displayPreference(root);mManageDeviceAdminPreferenceController.updateState(root.findPreference(KEY_MANAGE_DEVICE_ADMIN));mEnterprisePrivacyPreferenceController.displayPreference(root);mEnterprisePrivacyPreferenceController.onResume();/// M: Add plugin itemsPreferenceGroup deviceAdminCategory = (PreferenceGroup) root.findPreference(KEY_DEVICE_ADMIN_CATEGORY);addPluginEntrance(deviceAdminCategory);
+ root.findPreference(KEY_LOCATION).setVisible(false);return root;到这里,在设置的搜索框中输入定位关键字仍能搜索到相关功能选项,想要屏蔽掉的话具体修改参照如下:
/vendor/mediatek/proprietary/packages/apps/MtkSettings/src/com/android/settings/search/SearchIndexableResources.java
addIndex(LanguageAndInputSettings.class, NO_DATA_RES_ID, R.drawable.ic_settings_language);
- addIndex(LocationSettings.class, R.xml.location_settings, R.drawable.ic_settings_location);
- addIndex(ScanningSettings.class, R.xml.location_scanning, R.drawable.ic_settings_location);addIndex(SecuritySettings.class, NO_DATA_RES_ID, R.drawable.ic_settings_security);addIndex(EncryptionAndCredential.class, NO_DATA_RES_ID, R.drawable.ic_settings_security);重新编译验证,修改生效,设置中的定位功能已屏蔽
相关文章:

Android 8.1 隐藏设置中定位功能
Android 8.1 隐藏设置中定位功能 最近接到客户反馈,需要隐藏设备设置中的定位功能,具体修改参照如下: /vendor/mediatek/proprietary/packages/apps/MtkSettings/src/com/android/settings/SecuritySettings.java mLocationcontroller.displ…...
无线网卡怎么连接台式电脑?正确操作步骤分享!
“我在使用电脑时经常都需要用到网络,请问大家在使用无线网卡时怎么将它与台式电脑进行连接的呢?” 使用电脑的用户在进行网上冲浪时都需要先连接网络。如果不想使用网线,无线网卡不仅可以为用户提供网络服务,在使用时该更加灵活和…...
聚道云软件连接器助力某贸易公司实现付款流程自动化
客户介绍: 某贸易公司是一家集进出口贸易、国内贸易、电子商务等业务于一体的综合性贸易企业。公司业务遍及全球多个国家和地区,拥有庞大的供应商网络和采购需求。 添加图片注释,不超过 140 字(可选) 客户痛点&#…...

第六讲_css盒子模式
css盒子模型 1. 长度单位2. 盒子模型的组成2.1 盒子模型内容2.2 盒子模型内边距2.3 盒子模型边框2.4 盒子模型外边距 1. 长度单位 px:像素em:相对于当前元素或父元素的 font-size 的倍数 <style>.parent {height: 500px;width: 500px;background…...
【WSL】Win10 使用 WSL2 进行 Linux GPU 开发
1. GPU 驱动 先安装 驱动 参考 https://docs.nvidia.com/cuda/wsl-user-guide/index.html 使用 https://www.nvidia.com/Download/index.aspx 提供的兼容 GeForce 或 NVIDIA RTX/Quadro 显卡在系统上安装 NVIDIA GeForce Game Ready 或 NVIDIA RTX Quadro Windows 11 显示驱动…...

什么是博若莱新酒节?
在红酒圈儿里混,一定不能不知道博若莱新酒节,这是法国举世闻名的以酒为主题的重要节日之一。现已成为世界范围内庆祝当年葡萄收获和酿制的节日,被称为一年一度的酒迷盛会。 云仓酒庄的品牌雷盛红酒LEESON分享博若莱位于法国勃艮第南部&#x…...

Centos7下升级gcc/g++版本(简单 + 避坑)
在 Centos7 下,使用 yum 安装高版本的 gcc/g 最简单: yum -y install centos-release-scl yum -y install devtoolset-11-gcc devtoolset-11-gcc-c devtoolset-11-binutils需要安装哪个个版本的gcc/g,就把数字替换成对应的版本号。例如上面代…...
)
PyTorch项目源码学习(1)
PyTorch PyTorch是一个开源的深度学习框架,项目地址 https://github.com/pytorch/pytorch 在学术工作中的使用频率较高。 其主体由C开发,PyTorch是Torch的Python调用版本。学习PyTorch项目源代码的目的在于学习其中的实现方法与技巧,增加训练…...

adb 使用的出现 adb server is out of date. killing
我知道你们肯定看到这种播客 像这种解决问题的方法是暂时的 , 因为我们Android studio 中 , 你在查看后台的时候发现 你的Android studio 也占用了一端口 , 就是说你把 Android studio 杀掉了只要打开 Android studio 打开就还是 关闭 cmd adb 看到一个新的方法 , win 10 中…...

数据结构之二叉搜索树(Binary Search Tree)
数据结构可视化演示链接,也就是图片演示的网址 系列文章目录 数据结构之AVL Tree 数据结构之B树和B树 数据结构之Radix和Trie 文章目录 系列文章目录示例图定义二叉搜索树满足的条件应用场景 示例图 二叉 线形(顺序插入就变成了线性树,例如插入顺序为&…...

Spring Boot自定义启动Banner在线生成工具
记录一下,后续有更新添加 链接: Spring Boot自定义启动Banner在线生成工具...
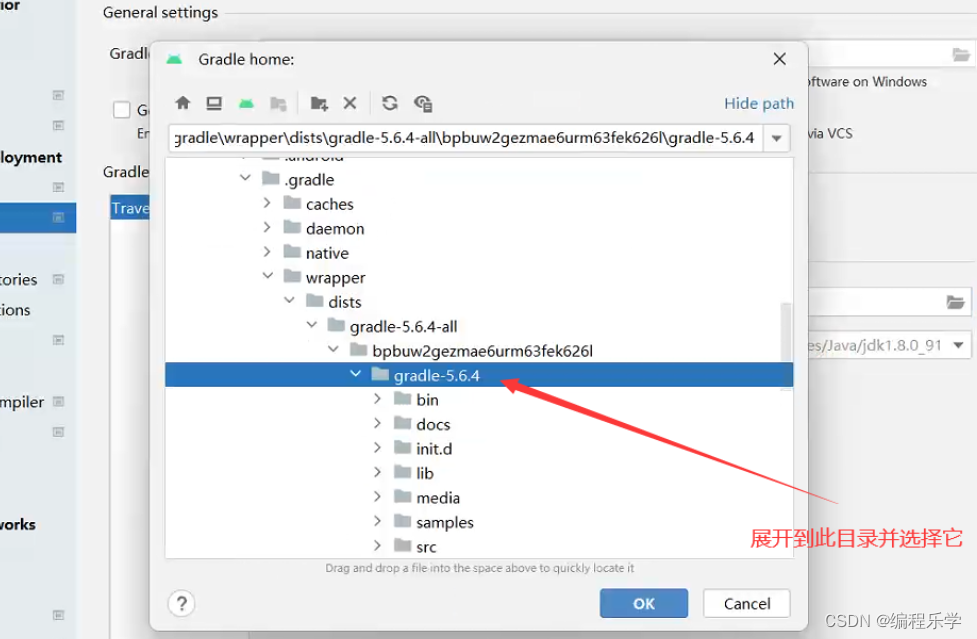
Android Studio导入项目 下载gradle很慢或连接超时,提示:Read timed out---解决方法建议收藏!
目录 前言 一、报错信息 二、解决方法 三、更多资源 前言 一般来说,使用Android Studio导入项目并下载gradle的过程应该是相对顺利的,但是有时候会遇到下载速度缓慢或连接超时的问题,这可能会让开发者感到头疼。这种情况通常会出现在网络…...
--FETK如何帮助Aurix实现快速原型、标定测量功能(1))
汽车标定技术(十五)--FETK如何帮助Aurix实现快速原型、标定测量功能(1)
目录 1.概述 2.ETK描述 2.1 产品概述 2.2 FETK-T1.1产品描述 2.3 FETK-T1.1内部构造 3.小结...

linux项目部署(jdk,tomcat,mysql,nginx,redis)
打开虚拟机,与连接工具连接好,创建一个文件夹 cd /tools 把jdk,tomcat安装包放入这个文件夹里面 jdk安装 #解压 tar -zxvf apache-tomcat-8.5.20.tar.gz #解压jdk tar -zxvf jdk-8u151-linux-x64.tar.gz 编辑jdk文件以及测试jdk安装 第一行代码路径…...
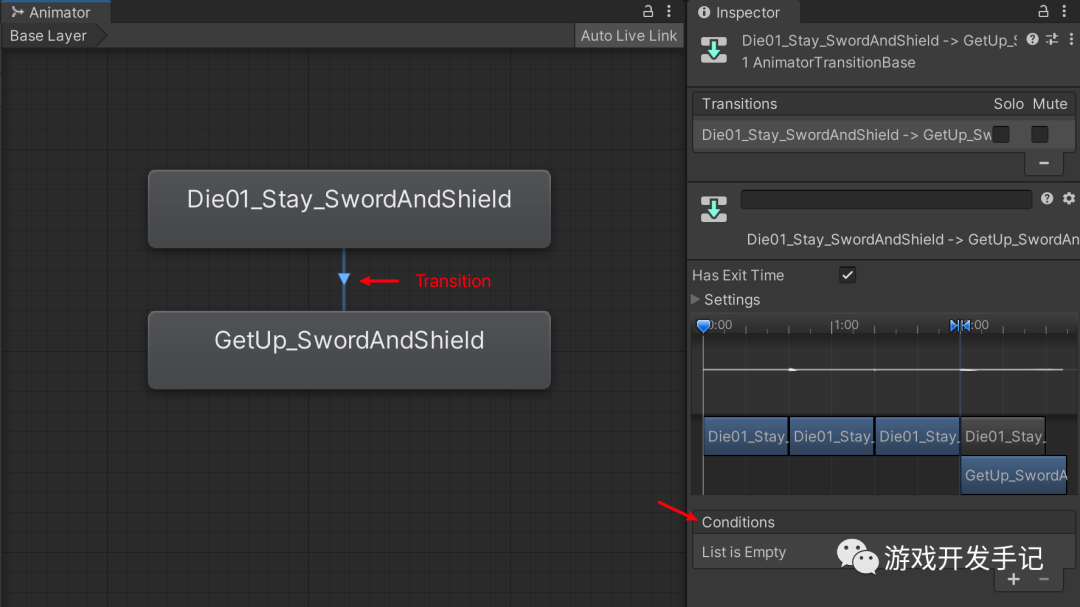
Unity | 渡鸦避难所-6 | 有限状态机控制角色行为逻辑
1 有限状态机简介 有限状态机(英语:finite-state machine,缩写:FSM),简称状态机,是表示有限个状态以及在这些状态之间的转移和动作等行为的数学计算模型 在游戏开发中应用有限状态机ÿ…...

数据库参数 PGA_AGGREGATE_LIMIT 限制进程大小
在自动化 PGA 内存管理模式下,Oracle 数据库通过动态控制分配到工作区的 PGA 内存量来尝试遵从 PGA_AGGREGATE_TARGET 值。但是,有时因为以下原因,PGA 内存使用量可能会超过 PGA_AGGREGATE_TARGET 设置: PGA_AGGREGATE_TARGET 设置…...
】停车场车辆统计(贪心算法实现-JavaPythonC++JS实现))
208.【2023年华为OD机试真题(C卷)】停车场车辆统计(贪心算法实现-JavaPythonC++JS实现)
🚀点击这里可直接跳转到本专栏,可查阅顶置最新的华为OD机试宝典~ 本专栏所有题目均包含优质解题思路,高质量解题代码(Java&Python&C++&JS分别实现),详细代码讲解,助你深入学习,深度掌握! 文章目录 一. 题目-停车场车辆统计二.解题思路三.题解代码Python题…...

JS 作用域和预解析
作用域 通常来说,一段程序代码中所用到的名字并不总是有效和可用的,而限定这个名字的可用性的代码范围就是这个名字的作用域。作用域的使用提高了程序逻辑的局部性,增强了程序的可靠性,减少了名字冲突。 作用域分为全局作用域和局…...

各种锁的概述
乐观锁与悲观锁 悲观锁指对数据被外界修改持保守态度,认为数据很容易就会被其他线程修改,所以在数据被处理前先对数据进行加锁,并在整个数据处理过程中,使数据处于锁定状态。 悲观锁的实现往往依靠数据库提供的锁机制࿰…...
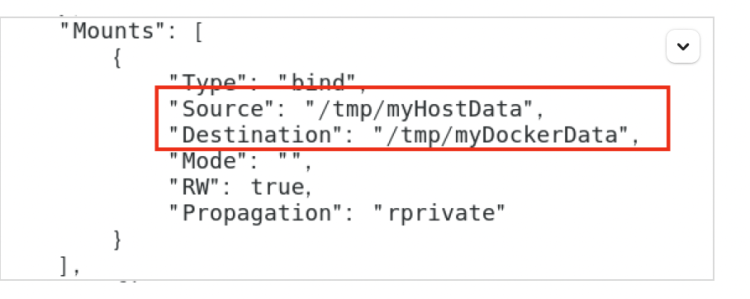
【docker笔记】Docker容器数据卷
Docker容器数据卷 卷就是目录或者文件,存在于一个或多个容器中,由docker挂载到容器,但不属于联合文件系统,因此能够绕过Union File System提供一些用于持续存储或共享数据的特性 卷的设计目的就是数据的持久化,完全独…...

变量 varablie 声明- Rust 变量 let mut 声明与 C/C++ 变量声明对比分析
一、变量声明设计:let 与 mut 的哲学解析 Rust 采用 let 声明变量并通过 mut 显式标记可变性,这种设计体现了语言的核心哲学。以下是深度解析: 1.1 设计理念剖析 安全优先原则:默认不可变强制开发者明确声明意图 let x 5; …...

智慧医疗能源事业线深度画像分析(上)
引言 医疗行业作为现代社会的关键基础设施,其能源消耗与环境影响正日益受到关注。随着全球"双碳"目标的推进和可持续发展理念的深入,智慧医疗能源事业线应运而生,致力于通过创新技术与管理方案,重构医疗领域的能源使用模式。这一事业线融合了能源管理、可持续发…...

LeetCode - 394. 字符串解码
题目 394. 字符串解码 - 力扣(LeetCode) 思路 使用两个栈:一个存储重复次数,一个存储字符串 遍历输入字符串: 数字处理:遇到数字时,累积计算重复次数左括号处理:保存当前状态&a…...

智能在线客服平台:数字化时代企业连接用户的 AI 中枢
随着互联网技术的飞速发展,消费者期望能够随时随地与企业进行交流。在线客服平台作为连接企业与客户的重要桥梁,不仅优化了客户体验,还提升了企业的服务效率和市场竞争力。本文将探讨在线客服平台的重要性、技术进展、实际应用,并…...

【决胜公务员考试】求职OMG——见面课测验1
2025最新版!!!6.8截至答题,大家注意呀! 博主码字不易点个关注吧,祝期末顺利~~ 1.单选题(2分) 下列说法错误的是:( B ) A.选调生属于公务员系统 B.公务员属于事业编 C.选调生有基层锻炼的要求 D…...

C# SqlSugar:依赖注入与仓储模式实践
C# SqlSugar:依赖注入与仓储模式实践 在 C# 的应用开发中,数据库操作是必不可少的环节。为了让数据访问层更加简洁、高效且易于维护,许多开发者会选择成熟的 ORM(对象关系映射)框架,SqlSugar 就是其中备受…...

GitFlow 工作模式(详解)
今天再学项目的过程中遇到使用gitflow模式管理代码,因此进行学习并且发布关于gitflow的一些思考 Git与GitFlow模式 我们在写代码的时候通常会进行网上保存,无论是github还是gittee,都是一种基于git去保存代码的形式,这样保存代码…...

毫米波雷达基础理论(3D+4D)
3D、4D毫米波雷达基础知识及厂商选型 PreView : https://mp.weixin.qq.com/s/bQkju4r6med7I3TBGJI_bQ 1. FMCW毫米波雷达基础知识 主要参考博文: 一文入门汽车毫米波雷达基本原理 :https://mp.weixin.qq.com/s/_EN7A5lKcz2Eh8dLnjE19w 毫米波雷达基础…...

DBLP数据库是什么?
DBLP(Digital Bibliography & Library Project)Computer Science Bibliography是全球著名的计算机科学出版物的开放书目数据库。DBLP所收录的期刊和会议论文质量较高,数据库文献更新速度很快,很好地反映了国际计算机科学学术研…...

多元隐函数 偏导公式
我们来推导隐函数 z z ( x , y ) z z(x, y) zz(x,y) 的偏导公式,给定一个隐函数关系: F ( x , y , z ( x , y ) ) 0 F(x, y, z(x, y)) 0 F(x,y,z(x,y))0 🧠 目标: 求 ∂ z ∂ x \frac{\partial z}{\partial x} ∂x∂z、 …...
