算法——贪心法(Greedy)
贪心法
- 把整个问题分解成多个步骤,在每个步骤都选取当前步骤的最优方案,直到所有步骤结束;在每一步都不考虑对后续步骤的影响,在后续步骤中也不再回头改变前面的选择。
- 不足之处:
- 贪心算法并不能保证获得全局最优解,但总能获得局部最优解
贪心算法只能确定某些问题的可行性范围
贪心算法可解决的问题通常大部分都有如下的特性:
1、有一个以最优方式来解决的问题。为了构造问题的解决方案,有一个候选的对象的集合:比如不同面值的硬币
2、随着算法的进行,将积累起其他两个集合:一个包含已经被考虑过并被选出的候选对象,另一个包含已经被考虑过但被丢弃的候选对象
3、有一个函数来检查一个候选对象的集合是否提供了问题的解答。该函数不考虑此时的解决方法是否最优
4、还有一个函数检查是否一个候选对象的集合是可行的,即是否可能往该集合上添加更多的候选对象以获得一个解。和上一个函数一样,此时不考虑解决方法的最优性
5、选择函数可以指出哪一个剩余的候选对象最有希望构成问题的解
6、最后,目标函数给出解的值
利用贪心法求解的问题应具备如下2个特征
1、贪心选择性质
一个问题的整体最优解可通过一系列局部的最优解的选择达到,并且每次的选择可以依赖以前作出的选择,但不依赖于后面要作出的选择。
2、最优子结构性质
当一个问题的最优解包含其子问题的最优解时,称此问题具有最优子结构性质。
与动态规划的区别
贪心算法与动态规划的不同在于它对每个子问题的解决方案都做出选择,不能回退。动态规划则会保存以前的运算结果,并根据以前的结果对当前进行选择,有回退功能。
一、 正整数分解使得乘积最大问题(贪心)
问题描述:
设n是一个正整数。现在要求将n分解为若干个自然数之和,且使这些自然数的乘积最大。
分析:
将这个大问题分解为两个小问题:
(1)这些自然数是互不相同的
(2)这些自然数可以是相同的
1不会增大乘积,反而会占据和,所以分解出的数中不应有 1
先找几个数作例子,找规律
注意应用到实际问题时,可能存在两个问题:
1、乘积出来的数太大,题目要求返回取余后的结果即可
解决办法:一边乘积,一边取余,而非全部乘积完成后取余
2、分解出来的数太多,把它们乘积到一起会超时
解决办法:快速幂(不用递归)
见下面的第二题
1、不同的自然数
将其分解成连续的整数,从2开始,2,3,4,……将剩余的数按照从后往前的次序一次均匀分配。
package no1_1;
import java.util.*;
public class Main {public static void main(String[] args) {Scanner input=new Scanner(System.in);int n=input.nextInt();int k=2; // 从2开始分解成连续的数// 创建一个包含100个整数的数组int in[]=new int[100];int i=0;// 把n分成2,3,4,……一组连续的数字while(n>=k) {in[i++]=k;n-=k;k++;}// 如果有剩余的数,从后往前加到前面分好的一组连续数字中if(n!=0) {// 如果分剩的数与上一个减数相同,先对其加1,才能保证前面的减数都能均匀分配if(n==in[i-1]) {in[i-1]++;n--;}// 从后往前均匀分配for(int j=0;j<n;j++) {in[i-1-j]++;}}// 初始化乘积result为1int result=1;// 计算最大乘积for(int j=0;j<=i-1;j++) {result*=in[j];}System.out.println(result);}
}2、可以有相同的自然数
主要将 n 分解成2和3,主要是3。
package no1_1;
import java.util.*;
public class Main {public static void main(String[] args) {Scanner input=new Scanner(System.in);int n=input.nextInt();// 创建一个包含100个整数的数组int in[]=new int[100];int i=0;// 当n不等于2和4时,按3进行分解while(n!=2 && n!=4) {in[i++]=3;n-=3;}// 当n不等于0时,按2继续分解while(n!=0) {in[i++]=2;n-=2;}// 初始化乘积result为1int result=1;// 计算最大乘积for(int j=0;j<=i-1;j++) {result*=in[j];}System.out.println(result);} }
二、数的潜能(贪心)
分析
- 快速幂:快速幂 - OI Wiki (oi-wiki.org)
package no1_1;
import java.util.*;
public class Main {public static void main(String[] args) {Scanner input=new Scanner(System.in);long n=input.nextLong();if(n==1) {System.out.println(1);}else {long threeNums=n/3;//n最多能分出多少个3int result=1;if(n%3==1) {//分解成threeNums个3和两个2,(4是特殊的例子,拆分成两个2时,乘积最大)threeNums--;result=4;}else if(n%3==2) {//分解成threeNums个3和一个2result=2;} result=binpow(result,3,threeNums,5218); System.out.println(result);} } //使用二进制快速幂算法计算 baseNumber 的 power 次幂对 modNumber 取模的结果public static int binpow(int result,int baseNumber,long power,int modNumber) {result%=modNumber;// 对底数取模,防止溢出baseNumber%=modNumber;// 对底数取模,防止溢出while(power>0) {if((power&1)==1) {result=result*baseNumber%modNumber;// 如果 幂 的当前位为 1,则更新结果}baseNumber=baseNumber*baseNumber%modNumber;// 底数自乘取模,相当于2次幂后取模power>>=1;//power 右移一位}return result;}
}三、最大分解
分析
- n=a0>a1>a2>……>ap,a(i+1)是a(i)的最大约数,
- 比如10>5>1, 5是10不等于自身的最大约数,1是5不等于自身的最大约数
- 找到每层不等于自身的最大约数即可
package no1_1;
import java.util.*;
public class Main {public static void main(String[] args) {Scanner input=new Scanner(System.in);int n=input.nextInt();long sum=0;while(n!=1) {//当n==1时,就不能再分解下去了//当i==n时,n为质数,不等于它自身的最大约数即为1for(int i=2;i<=n;i++) {if(n%i==0) {n=n/i;sum+=n;break;}}}System.out.println(sum);}
}
相关文章:

算法——贪心法(Greedy)
贪心法 把整个问题分解成多个步骤,在每个步骤都选取当前步骤的最优方案,直到所有步骤结束;在每一步都不考虑对后续步骤的影响,在后续步骤中也不再回头改变前面的选择。不足之处: 贪心算法并不能保证获得全局最优解&…...

VmWare虚拟机的安装
VmWare官方最新版下载地址 vmware官方下载地址 安装流程 安装成功验证 安装完成之后,打开网络中心,一定要确认这里多出两个网络连接,才证明Vmware已经安装成功...
Vue.js轻量级框架:快速搭建可扩展的管理系统
一、前言 在项目实战开发中,尤其是大平台系统的搭建,针对不同业务场景,需要为用户多次编写用于录入、修改、展示操作的相应表单页面。一旦表单需求过多,对于开发人员来说,算是一种重复开发,甚至是繁杂的工作…...
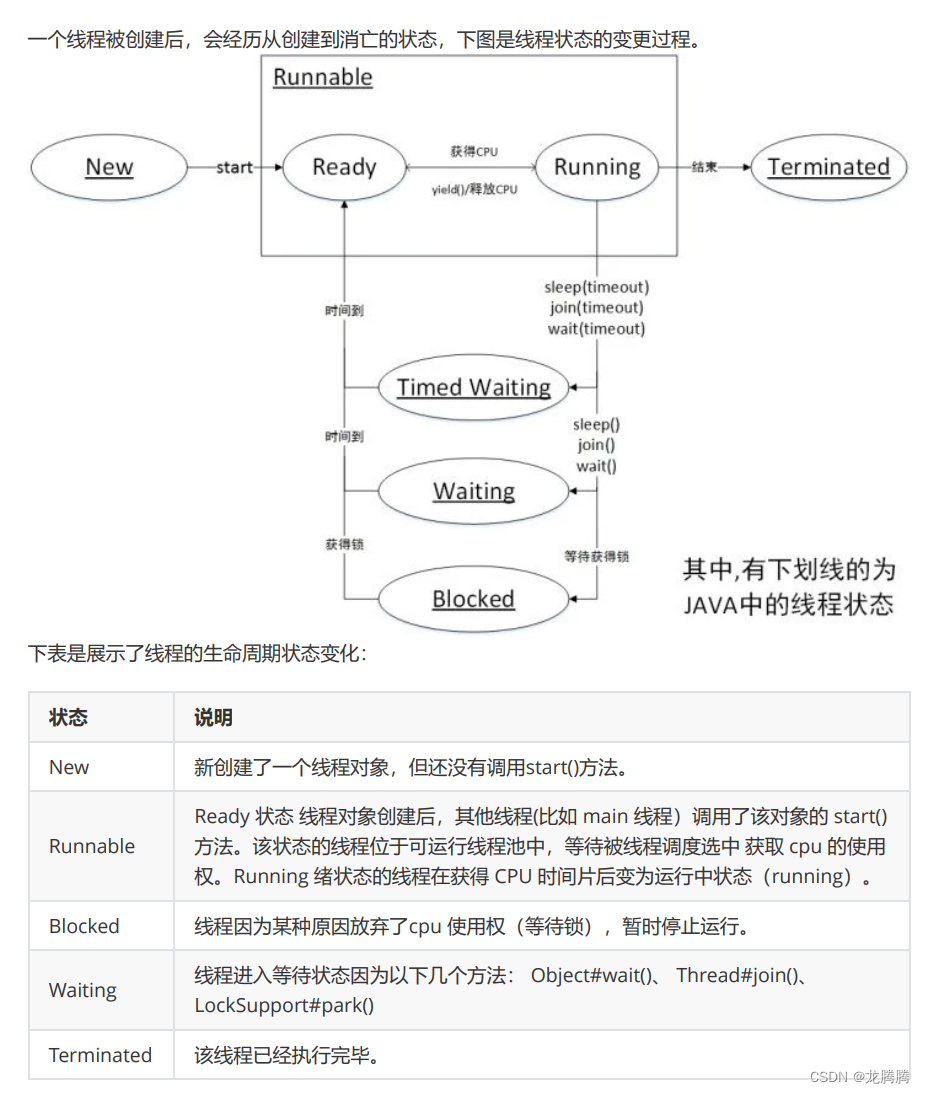
Android-多线程
线程是进程中可独立执行的最小单位,也是 CPU 资源(时间片)分配的基本单位,同一个进程中的线程可以共享进程中的资源,如内存空间和文件句柄。线程有一些基本的属性,如id、name、以及priority。 id࿱…...

sqlalchemy 监听所有实体插入以及更新事件
这边使用的是flaskdependency-injectersqlalchemy,有一个公共类,想插入或者更新的时候对公共类某些字段进行统一操作 这个是公共类:包括一些基础字段,所有的实体都会继承这个类 """Models module.""&q…...

go怎么结束很多个协程呢
在Go语言中,可以通过使用context来结束多个协程。context包提供了用于跟踪、取消和传递截止日期的机制,可用于协程的生命周期管理。 以下是一个使用context取消多个协程的示例: package mainimport ("context""fmt"&qu…...

springboot 项目访问静态资源遇到的问题,WebMvcConfigurer和WebMvcConfigurationSupport
之前发过通过继承WebMvcConfigurationSupport来访问静态资源的文章——img标签访问静态资源,代码如下 Configuration public class LocalPathWebMvcConfigurer extends WebMvcConfigurationSupport {/*** 在springboot项目中,允许浏览器访问指定本地文件…...
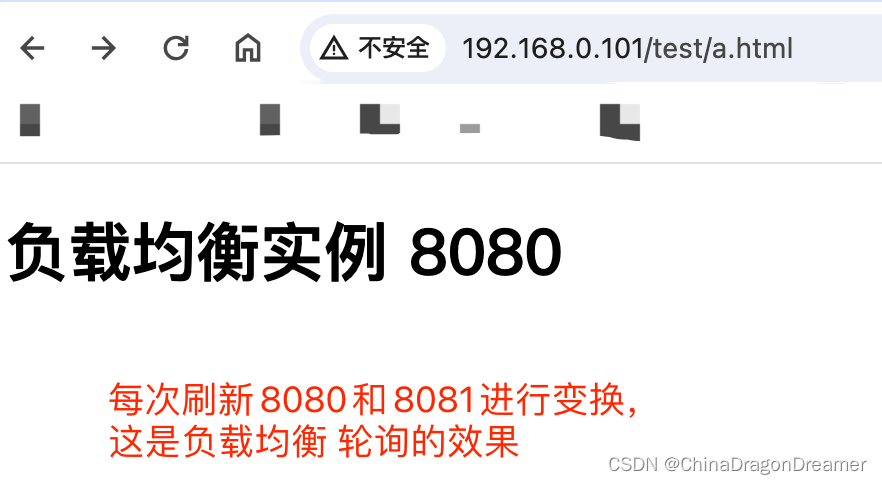
Nginx配置负载均衡实例
Nginx配置反向代理实例二 提醒一下:下面实例讲解是在Mac系统演示的; 负载均衡实例实现的效果 浏览器地址栏输入地址http://192.168.0.101/test/a.html,刷新页面进行多次请求,负载均衡效果,平均分配到8080端口服务和8…...
)
【算法题】50. Pow(x, n)
题目 实现 pow(x, n) ,即计算 x 的整数 n 次幂函数(即,xn )。 示例 1: 输入:x 2.00000, n 10 输出:1024.00000 示例 2: 输入:x 2.10000, n 3 输出:9.…...

K8S动态PV
pv和pvc存储卷 存储卷: emptyDir容器内部,随着pod销毁,emptyDir也会消失,不能做数据持久化 hostPath:持久化存储数据,可以和节点上目录做挂载。pod被销毁了数据还在 NFS:一台机器࿰…...
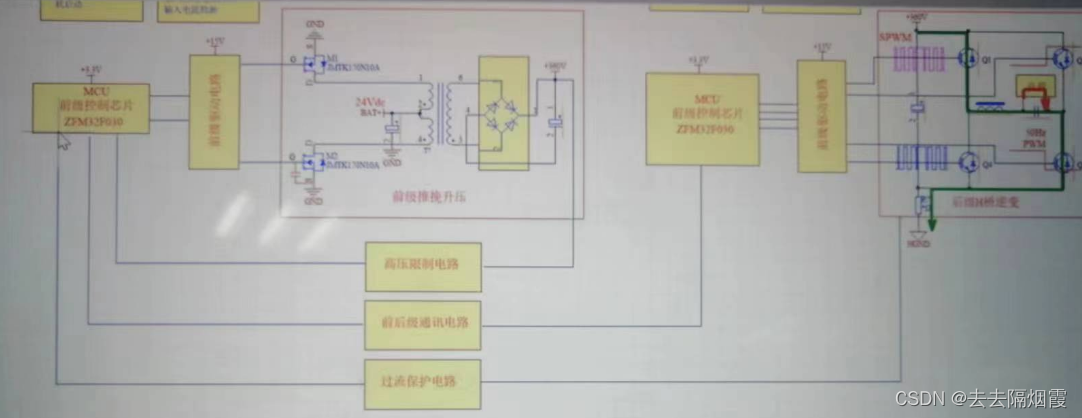
逆变器2(原理框图)
总流程 输入(低压直流24Vdc)——升压(DC—DC)(高压直流369Vdc) ——逆变(DC—AC)(交流220V) 升压电路:BOOST电路、LLC电路、推挽电路 逆变器过程…...

ERA5合集,使用ERA5得到GNSS站点的温度,气压,水汽压,Tm和PWV合集,可以求五个参数
0. 码字不易,点赞加关注(公众号:WZZHHH,部分资料在公众号可以下载),使用请注明出处(根据我的研究方向,我会不断更新代码)。 1.计算PWV的方法一般采用有三种, …...

c#让三个线程按照顺序执行
现实的例子 三个线程都是while(true)的循环体 A线程:采集数据 B线程:画曲线 C线程:存数据库 AutoResetEvent类 AutoResetEvent 是一个线程同步的类,它提供了一种机制,允许一个或多个线程等待直…...

AWS Directory Service 开启ldaps
启用客户端 LDAPS 要启用客户端 LDAPS,您需要将证书颁发机构(CA)证书导入 AWS Managed Microsoft AD,然后在目录上启用 LDAPS。启用后,AWS 应用程序与您自行管理的 Active Directory 之间的所有 LDAP 通信将通过安全套…...

Seata 以 Nacos 为注册中心启动
Seata 以 Nacos 为注册中心启动 修改 conf 下的 application.yml 配置 server:port: 7091spring:application:name: seata-serverlogging:config: classpath:logback-spring.xmlfile:path: ${user.home}/logs/seataextend:logstash-appender:destination: 127.0.0.1:4560kafk…...
Unity填坑-灯光烘焙相关
Unity填坑-灯光烘焙相关 文章目录 Unity填坑-灯光烘焙相关前言一、Light的模式二、光的效果分类三、各种Light模式与烘焙的说明1.Realtime,实时光2.baked,烘焙光3.mixed,混合 四、实时全局光五、其他说明1.动态物体的全局光照效果2.手机使用烘焙注意的点3.其他设置 前言 项目组…...

【python】TCP测速程序
一、服务端 下面是一个简单的 Python 服务端程序的示例,使用标准库中的 socket 模块来建立一个 TCP 服务器。该服务器接收客户端的连接请求,客户端发送一定大小的数据流以测试 TCP 带宽。 实际场景中带宽测试可能需要更复杂的逻辑来确保测试的准确性。 …...

新书速览|从零开始大模型开发与微调:基于PyTorch与ChatGLM
详细讲解大模型基本理论、算法、程序实现与应用实战,揭示大模型开发与微调技术 1 本书内容 大模型是深度学习自然语言处理皇冠上的一颗明珠,也是当前AI和NLP研究与产业中最重要的方向之一。本书使用PyTorch 2.0作为学习大模型的基本框架,以C…...

边缘计算:连接实时数据的力量与未来发展之路
边缘计算是一种分布式计算范式,它旨在将数据处理、存储和应用服务带到数据源的近端,即网络的“边缘”。在边缘计算模型中,算力和存储资源距离末端用户或数据源更近,这减少了数据在网络中传输的距离,从而降低延迟&#…...

ZooKeeper 实战(四) Curator Watch事件监听
文章目录 ZooKeeper 实战(四) Curator Watch事件监听0.前言1.Watch 事件监听概念2.NodeCache2.1.全参构造器参数2.2.代码DEMO2.3.日志输出 3.PathChildrenCache3.1.全参构造器参数3.2.子节点监听时间类型3.2.代码DEMO 4.TreeCache4.1.构造器参数4.2.代码DEMO4.3.日志输出 ZooKe…...

前端倒计时误差!
提示:记录工作中遇到的需求及解决办法 文章目录 前言一、误差从何而来?二、五大解决方案1. 动态校准法(基础版)2. Web Worker 计时3. 服务器时间同步4. Performance API 高精度计时5. 页面可见性API优化三、生产环境最佳实践四、终极解决方案架构前言 前几天听说公司某个项…...

《从零掌握MIPI CSI-2: 协议精解与FPGA摄像头开发实战》-- CSI-2 协议详细解析 (一)
CSI-2 协议详细解析 (一) 1. CSI-2层定义(CSI-2 Layer Definitions) 分层结构 :CSI-2协议分为6层: 物理层(PHY Layer) : 定义电气特性、时钟机制和传输介质(导线&#…...

《Playwright:微软的自动化测试工具详解》
Playwright 简介:声明内容来自网络,将内容拼接整理出来的文档 Playwright 是微软开发的自动化测试工具,支持 Chrome、Firefox、Safari 等主流浏览器,提供多语言 API(Python、JavaScript、Java、.NET)。它的特点包括&a…...

MVC 数据库
MVC 数据库 引言 在软件开发领域,Model-View-Controller(MVC)是一种流行的软件架构模式,它将应用程序分为三个核心组件:模型(Model)、视图(View)和控制器(Controller)。这种模式有助于提高代码的可维护性和可扩展性。本文将深入探讨MVC架构与数据库之间的关系,以…...

【单片机期末】单片机系统设计
主要内容:系统状态机,系统时基,系统需求分析,系统构建,系统状态流图 一、题目要求 二、绘制系统状态流图 题目:根据上述描述绘制系统状态流图,注明状态转移条件及方向。 三、利用定时器产生时…...

实现弹窗随键盘上移居中
实现弹窗随键盘上移的核心思路 在Android中,可以通过监听键盘的显示和隐藏事件,动态调整弹窗的位置。关键点在于获取键盘高度,并计算剩余屏幕空间以重新定位弹窗。 // 在Activity或Fragment中设置键盘监听 val rootView findViewById<V…...

Android Bitmap治理全解析:从加载优化到泄漏防控的全生命周期管理
引言 Bitmap(位图)是Android应用内存占用的“头号杀手”。一张1080P(1920x1080)的图片以ARGB_8888格式加载时,内存占用高达8MB(192010804字节)。据统计,超过60%的应用OOM崩溃与Bitm…...

使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台
🎯 使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台 📌 项目背景 随着大语言模型(LLM)的广泛应用,开发者常面临多个挑战: 各大模型(OpenAI、Claude、Gemini、Ollama)接口风格不统一;缺乏一个统一平台进行模型调用与测试;本地模型 Ollama 的集成与前…...

ip子接口配置及删除
配置永久生效的子接口,2个IP 都可以登录你这一台服务器。重启不失效。 永久的 [应用] vi /etc/sysconfig/network-scripts/ifcfg-eth0修改文件内内容 TYPE"Ethernet" BOOTPROTO"none" NAME"eth0" DEVICE"eth0" ONBOOT&q…...

【生成模型】视频生成论文调研
工作清单 上游应用方向:控制、速度、时长、高动态、多主体驱动 类型工作基础模型WAN / WAN-VACE / HunyuanVideo控制条件轨迹控制ATI~镜头控制ReCamMaster~多主体驱动Phantom~音频驱动Let Them Talk: Audio-Driven Multi-Person Conversational Video Generation速…...






