六、栈、栈的相关问题
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档
目录
前言
一、栈
1.栈概述
2.栈的实现
2.1 栈的API
2.2 栈的实现
二、栈的括号匹配问题
1.问题描述
2.代码实现
三、逆波兰表达式求值问题
1.问题描述
2.代码
总结
前言
提示:这里可以添加本文要记录的大概内容:
自学JAVA数据结构笔记,跟学视频为:黑马程序员Java数据结构与java算法全套教程,数据结构+算法教程全资料发布,包含154张java数据结构图_哔哩哔哩_bilibili
提示:以下是本篇文章正文内容,下面案例可供参考
一、栈
1.栈概述
栈是一种基于先进后出(FILO)的数据结构,是一种只能在一端进行插入和删除操作的特殊线性表。它按照先进后出 的原则存储数据,先进入的数据被压入栈底,最后的数据在栈顶,需要读数据的时候从栈顶开始弹出数据(最后一 个数据被第一个读出来)。
2.栈的实现
2.1 栈的API
类名 Stack
构造方法 Stack():创建Stack对象
成员方法 1.public boolean isEmpty():判断栈是否为空,是返回true,否返回false 2.public int size():获取栈中元素的个数
3.public T pop():弹出栈顶元素
4.public void push(T t):向栈中压入元素t
成员变量 1.private Node head:记录首结点
2.private int N:当前栈的元素个数
2.2 栈的实现
package List;import java.util.Iterator;/*
* 使用链表实现栈
* */
public class Stack <T> implements Iterable<T>{private Node head;private int N;//结点类private class Node{private T item;private Node next;public Node(T item, Node next){this.item = item;this.next = next;}}//构造函数public Stack(){this.head = new Node(null,null);this.N = 0;}//判断栈是否为空public boolean isEmpty(){return N == 0;}//返回栈长度public int size(){return N;}//把t元素压入栈public void push(T t){//第一个结点Node first = head.next;//创建新结点//由于栈的特点是先入后出,使用新压入的结点为链表的第一个结点Node newNode = new Node(t,first);head.next = newNode;N ++;}//出栈public T pop(){//出栈结点Node curr = head.next;if(curr == null){return null;}//头结点的下一个结点指向要删除结点的下一个结点‘head.next = curr.next;N --;return curr.item;}//实现迭代器@Overridepublic Iterator<T> iterator() {return new STiterator();}private class STiterator implements Iterator{private Node curr;public STiterator(){this.curr = head;}@Overridepublic boolean hasNext(){return curr.next != null;}@Overridepublic Object next() {curr = curr.next;return curr.item;}}}
二、栈的括号匹配问题
1.问题描述
给定一个字符串,里边可能包含"()"小括号和其他字符,请编写程序检查该字符串的中的小括号是否成对出现。
例如:
"(上海)(长安)":正确匹配
"上海((长安))":正确匹配
"上海(长安(北京)(深圳)南京)":正确匹配
"上海(长安))":错误匹配
"((上海)长安":错误匹配
2.代码实现
package Stack;import java.util.Scanner;public class BracketsMatch {public static void main(String[] args) {//创建字符串Scanner input = new Scanner(System.in);String str = "上海(长安))";//判断是否是有效括号boolean match = isMatch(str);if(match){System.out.println("正确匹配");}else{System.out.println("错误匹配");}}public static boolean isMatch(String str){//创建栈对象//1.创建一个栈用来存储左括号Stack<String> chars = new Stack<String>();//2.从左往右遍历字符串,拿到每一个字符for (int i = 0; i < str.length(); i++) {String curr = str.charAt(i) + "";//3.判断该字符是不是左括号,如果是,放入栈中存储if (curr.equals("(")) {chars.push(curr);} else if (curr.equals(")")) {//4.判断该字符是不是右括号,如果不是,继续下一次循环//5.如果该字符是右括号,则从栈中弹出一个元素t;String res = chars.pop();//6.判断元素t是否为null,如果不是,则证明有对应的左括号,如果不是,则证明没有对应的左括号if (res == null) {return false;}}}//7.循环结束后,判断栈中还有没有剩余的左括号,如果有,则不匹配,如果没有,则匹配return chars.size() == 0;}
}
三、逆波兰表达式求值问题
1.问题描述
逆波兰表达式求值问题是我们计算机中经常遇到的一类问题,要研究明白这个问题,首先我们得搞清楚什么是逆波 兰表达式?要搞清楚逆波兰表达式,我们得从中缀表达式说起。
中缀表达式:
中缀表达式就是我们平常生活中使用的表达式,例如:
1+3*2,2-(1+3)等等,
中缀表达式的特点是:二元运算符总 是置于两个操作数中间。
中缀表达式是人们最喜欢的表达式方式,因为简单,易懂。但是对于计算机来说就不是这样了,因为中缀表达式的 运算顺序不具有规律性。不同的运算符具有不同的优先级,如果计算机执行中缀表达式,需要解析表达式语义,做大量的优先级相关操作。
逆波兰表达式(后缀表达式):
逆波兰表达式是波兰逻辑学家J・卢卡西维兹(J・ Lukasewicz)于1929年首先提出的一种表达式的表示方法,后缀表 达式的特点:运算符总是放在跟它相关的操作数之后。
| 中缀表达式 | 逆波兰表达式 |
| a+b | ab+ |
| a+(b-c) | abc-+ |
| a+(b-c)*d | abc-d*+ |
| a*(b-c)+d | abc-*d+ |
2.代码
package Stack;public class ReversePolishNotation {public static void main(String[] args) {//中缀表达式3*(17-15)+18/6的逆波兰表达式如下String[] notation = {"3", "17", "15", "-", "*", "18", "6", "/", "+"};int result = caculate(notation);System.out.println("逆波兰表达式的结果为:" + result);}/*** @param notaion 逆波兰表达式的数组表示方式* @return 逆波兰表达式的计算结果*/public static int caculate(String[] notaion) {//1.创建一个栈对象oprands存储操作数Stack<Integer> oprands = new Stack<Integer>();//2.从左往右遍历逆波兰表达式,得到每一个字符串for (String curr : notaion) {//3.判断该字符串是不是运算符,如果不是,把该该操作数压入oprands栈中Integer o1;Integer o2;Integer result;switch (curr) {case "+"://4.如果是运算符,则从oprands栈中弹出两个操作数o1,o2o1 = oprands.pop();o2 = oprands.pop();//5.使用该运算符计算o1和o2,得到结果resultresult = o2 + o1;//6.把该结果压入oprands栈中oprands.push(result);break;case "-"://4.如果是运算符,则从oprands栈中弹出两个操作数o1,o2o1 = oprands.pop();o2 = oprands.pop();//5.使用该运算符计算o1和o2,得到结果resultresult = o2 - o1;//6.把该结果压入oprands栈中oprands.push(result);break;case "*"://4.如果是运算符,则从oprands栈中弹出两个操作数o1,o2o1 = oprands.pop();o2 = oprands.pop();//5.使用该运算符计算o1和o2,得到结果resultresult = o2 * o1;//6.把该结果压入oprands栈中oprands.push(result);break;case "/"://4.如果是运算符,则从oprands栈中弹出两个操作数o1,o2o1 = oprands.pop();o2 = oprands.pop();//5.使用该运算符计算o1和o2,得到结果resultresult = o2 / o1;//6.把该结果压入oprands栈中oprands.push(result);break;default:oprands.push(Integer.parseInt(curr));break;}}//7.遍历结束后,拿出栈中最终的结果返回Integer result = oprands.pop();return result;}
}总结
提示:这里对文章进行总结:
相关文章:

六、栈、栈的相关问题
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 目录 前言 一、栈 1.栈概述 2.栈的实现 2.1 栈的API 2.2 栈的实现 二、栈的括号匹配问题 1.问题描述 2.代码实现 三、逆波兰表达式求值问题 1.问题描述 2.代码 总结 前言 提…...

Java安全停止线程
Thread 类虽提供了一个 stop() 方法(已经被废弃),但由于 stop() 方法强制终止一个正在执行的线程,可能会造成数据不一致的问题,所以在生产环境中最好不要使用。 场景: 由于一些操作需要轮询处理ÿ…...
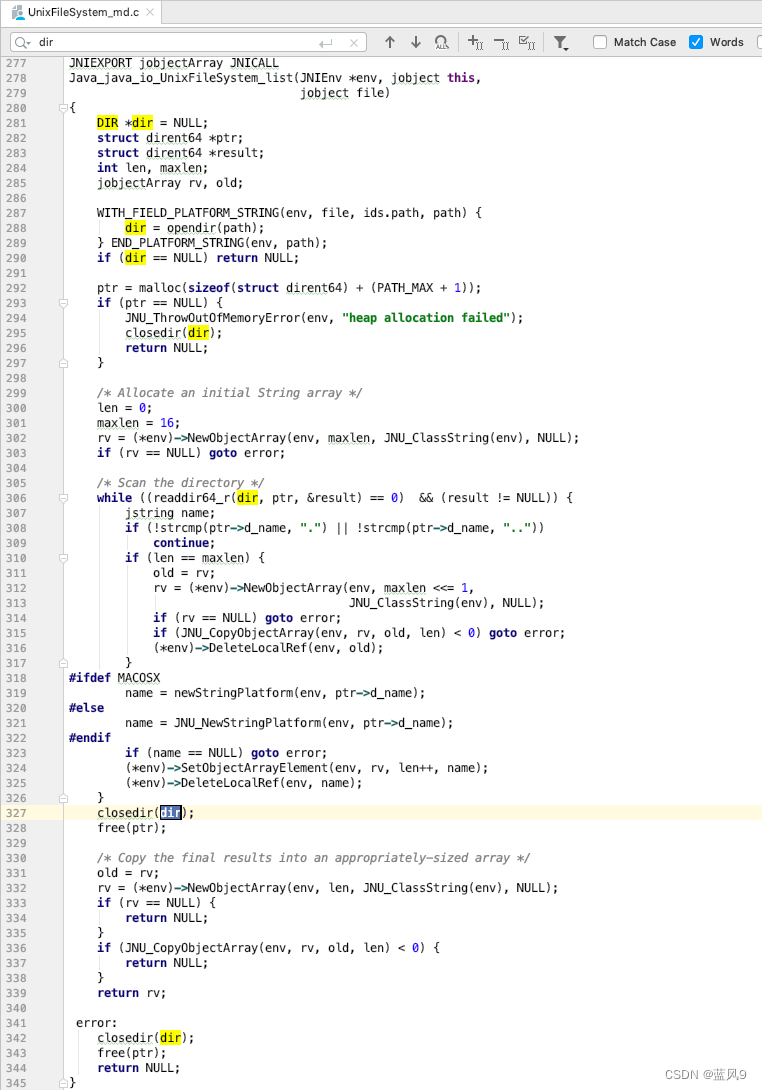
12 readdir 函数
前言 在之前 ls 命令 中我们可以看到, ls 命令的执行也是依赖于 opendir, readdir, stat, lstat 等相关操作系统提供的相关系统调用来处理业务 因此 我们这里来进一步看一下 更细节的这些 系统调用 我们这里关注的是 readdir 这个函数, 入口系统调用是 getdents 如下调试…...

Windows环境搭建Android开发环境-Android Studio/Git/JDK
Windows环境搭建Android开发环境-Android Studio/Git/JDK 因为休假回来后公司的开发环境由Ubuntu变为了Windows,所以需要重新配置一下开发环境。 工作多年第一次使用Windows环境进行开发工作,作次记录下来。 一、 Git安装 1.1git 标题软件下载 网址&…...

全国爱耳日丨听力受损严重有哪些解决办法
——【科学爱耳护耳,实现主动健康】随着数码电子设备使用越来越方便、日常使用时间越来越长,听力障碍、患上耳道疾病一系列问题也接踵而至,在当下我们必须重视听力健康,采取更科学的听音方式,保护听力健康,…...

【抽水蓄能电站】基于粒子群优化算法的抽水蓄能电站的最佳调度方案研究(Matlab代码实现)
👨🎓个人主页:研学社的博客💥💥💞💞欢迎来到本博客❤️❤️💥💥🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密…...
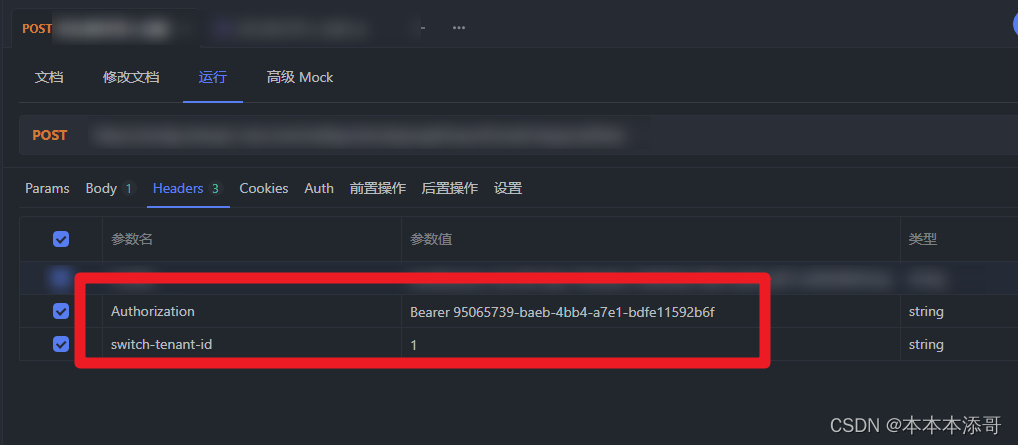
【异常】因多租户字段缺少导致Error updating database. Column ‘tenant_id‘ cannot be null
一、报错内容 org.springframework.dao.DataIntegrityViolationException: ### Error updating database. Cause: java.sql.SQLIntegrityConstraintViolationException: Column tenant_id cannot be null ### The error may exist in com/xxx/cloud/mall/admin/mapper/Goods…...

类和对象(上)
文章目录 面向对象的初步认知类的实例化this引用对象的构造及初始化封装static成员代码块内部类 对象的打印一、面向对象的初步认知 Java是一门纯面向对象的语言(Object Oriented Program,简称OOP),在面向对象的世界里,一切皆为对象。在java中…...

Java经典面试题——谈谈 Java 反射机制,动态代理是基于什么原理?
典型回答 反射机制是 Java 语言提供的一种基本功能,赋予程序在运行时 自省(introspect,官方用语)的能力。通过反射我们可以直接操作类或者对象,比如获取某个对象的类定义,获取类声明的属性和方法ÿ…...

19 客户端服务订阅机制的核心流程
Nacos客户端服务订阅机制的核心流程 说起Nacos的服务订阅机制,大家会觉得比较难理解,那我们就来详细分析一下,那我们先从Nacos订阅的概述说起 Nacos订阅概述 Nacos的订阅机制,如果用一句话来描述就是:Nacos客户端通…...
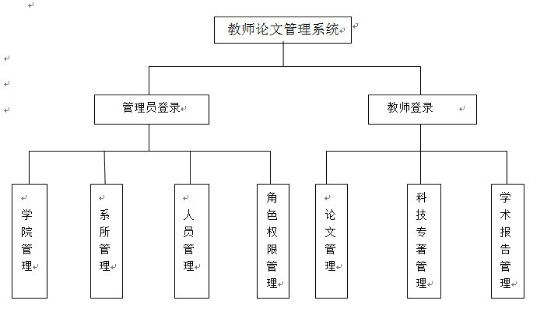
教师论文|科技专著管理系统
技术:Java、JSP等摘要:随着计算机和互联网技术的发展,社会的信息化程度越来越高,各行各业只有适应这种发展趋势,才能增强自己的适应能力和竞争能力,不断发展壮大。大学作为教育的基地,是社会进步…...

骨传导耳机是什么意思,骨传导耳机的好处具体有哪些
在这个全民都是手机的时代,各种蓝牙耳机,入耳式耳机,真无线耳机等各种款式琳琅满目。而骨传导耳机是一种全新的科技产物,顾名思义就是通过头骨振动将声音传至外耳内的耳机。由于无需入耳,不会对耳朵造成任何影响。那…...

elasticsearch—使用汇总
文档结构1、概念简介2、使用创景3、核心组件4、环境部署5、操作实践官方网站:https://www.elastic.co/cn/elasticsearch/ 官方手册:https://www.elastic.co/guide/en/elasticsearch/reference/8.6/getting-started.html 参考教程: Aÿ…...

聊一聊代码重构——我们为什么要代码重构
代码重构 事情的起因是在去年下半年,我们终于无法承受往年的历史包袱而决定开始进行代码重构。 在以前我们尝试过进行代码重构但是从来没有系统性的考虑过如何重构。在对代码重构的过程中很多经验都是来自《重构:改善既有代码的设计》这本书,…...

【Python学习笔记】第二十九节 Python2 和Python3发生了哪些变化
Python 版本分为两大流派,一个是 Python 2.x 版本,另外一个是 Python 3.x 版本,Python 官方同时提供了对这两个版本的支持和维护。2020 年 1 月 1 日,Python 官方终止了对 Python 2.7 版本(最后一个 Python 2.x 版本&a…...

[oeasy]python0099_雅达利大崩溃_IBM的开放架构_兼容机_oem
雅达利大崩溃 回忆上次内容 个人计算机浪潮已经来临 苹果公司迅速发展微软公司脱离mits准备做纯软件公司IBM用大型机思路制作的5100惨败 Commodore 64 既做计算机又做游戏机 计算机行业和游戏行业 跟随着底层技术不断迭代已经进入了战乱纷纷的年代最终又会如何呢?…...

学术论文投稿之同行评审过程中可能会遭遇哪些偏见?
同行评审过程的顺利进行,在很大程度上取决于学术界的积极参与和相互信任,以及需要参与各方都以负责任的态度行事。作为审稿专家,向作者提供公正、客观的评价是至关重要的。同行评审过程中,若有任何偏离客观性的行为,均…...
Python写一个自动发送直播弹幕的工具,非常简单
哈喽大家好,今天给大家用Python整一个可以在直播间自动发弹幕的工具,来为喜欢的主播疯狂扣6 ! 事情原由昨晚回家,表弟在看LOL直播,看得我气不打一处来,差点就想锤他。 身为程序员的表弟,看直…...

学生档案管理系统的设计与实现
技术:Java、JSP等摘要:本设计是为托普学院学生档案的管理实现电子化而设计的,系统开发采用J2EE技术,数据库采用了SQL Server 2005,因而系统具有很好的扩展性、可移植性,实现了教学资源的信息化管理。主要功…...

JavaEE学习笔记-SpringBoot快速上手、部分注解解释
SpringBoot快速上手 一、快速创建SpringBoot应用1.1利用IDEA提供的Spring Initializr创建Spring Boot应用1.2Spring Boot生成的项目结构介绍1.3初步测试后端是否OK(建立一个controll类)二、热部署2.1 添加依赖2.2 Setting处项目自动化设置2.3 具体项目设置2.4 待选步骤三、注…...

visual studio 2022更改主题为深色
visual studio 2022更改主题为深色 点击visual studio 上方的 工具-> 选项 在选项窗口中,选择 环境 -> 常规 ,将其中的颜色主题改成深色 点击确定,更改完成...

iPhone密码忘记了办?iPhoneUnlocker,iPhone解锁工具Aiseesoft iPhone Unlocker 高级注册版分享
平时用 iPhone 的时候,难免会碰到解锁的麻烦事。比如密码忘了、人脸识别 / 指纹识别突然不灵,或者买了二手 iPhone 却被原来的 iCloud 账号锁住,这时候就需要靠谱的解锁工具来帮忙了。Aiseesoft iPhone Unlocker 就是专门解决这些问题的软件&…...

OkHttp 中实现断点续传 demo
在 OkHttp 中实现断点续传主要通过以下步骤完成,核心是利用 HTTP 协议的 Range 请求头指定下载范围: 实现原理 Range 请求头:向服务器请求文件的特定字节范围(如 Range: bytes1024-) 本地文件记录:保存已…...

【git】把本地更改提交远程新分支feature_g
创建并切换新分支 git checkout -b feature_g 添加并提交更改 git add . git commit -m “实现图片上传功能” 推送到远程 git push -u origin feature_g...

Rust 异步编程
Rust 异步编程 引言 Rust 是一种系统编程语言,以其高性能、安全性以及零成本抽象而著称。在多核处理器成为主流的今天,异步编程成为了一种提高应用性能、优化资源利用的有效手段。本文将深入探讨 Rust 异步编程的核心概念、常用库以及最佳实践。 异步编程基础 什么是异步…...

pikachu靶场通关笔记22-1 SQL注入05-1-insert注入(报错法)
目录 一、SQL注入 二、insert注入 三、报错型注入 四、updatexml函数 五、源码审计 六、insert渗透实战 1、渗透准备 2、获取数据库名database 3、获取表名table 4、获取列名column 5、获取字段 本系列为通过《pikachu靶场通关笔记》的SQL注入关卡(共10关࿰…...
)
是否存在路径(FIFOBB算法)
题目描述 一个具有 n 个顶点e条边的无向图,该图顶点的编号依次为0到n-1且不存在顶点与自身相连的边。请使用FIFOBB算法编写程序,确定是否存在从顶点 source到顶点 destination的路径。 输入 第一行两个整数,分别表示n 和 e 的值(1…...

DeepSeek 技术赋能无人农场协同作业:用 AI 重构农田管理 “神经网”
目录 一、引言二、DeepSeek 技术大揭秘2.1 核心架构解析2.2 关键技术剖析 三、智能农业无人农场协同作业现状3.1 发展现状概述3.2 协同作业模式介绍 四、DeepSeek 的 “农场奇妙游”4.1 数据处理与分析4.2 作物生长监测与预测4.3 病虫害防治4.4 农机协同作业调度 五、实际案例大…...

有限自动机到正规文法转换器v1.0
1 项目简介 这是一个功能强大的有限自动机(Finite Automaton, FA)到正规文法(Regular Grammar)转换器,它配备了一个直观且完整的图形用户界面,使用户能够轻松地进行操作和观察。该程序基于编译原理中的经典…...

招商蛇口 | 执笔CID,启幕低密生活新境
作为中国城市生长的力量,招商蛇口以“美好生活承载者”为使命,深耕全球111座城市,以央企担当匠造时代理想人居。从深圳湾的开拓基因到西安高新CID的战略落子,招商蛇口始终与城市发展同频共振,以建筑诠释对土地与生活的…...
