【机器学习前置知识】狄利克雷分布
在阅读本文前,建议先食用以下几篇文章以能更好地理解狄利克雷分布:
二项分布
Beta分布
多项分布
共轭分布
狄利克雷分布
狄利克雷分布(Dirichlet distribution)是Beta分布的扩展,把Beta分布从二元扩展到多元形式就是狄利克雷分布,Beta分布是狄利克雷分布的二元特例。
在共轭方面,可以类比Beta分布与二项分布的关系,狄利克雷分布是多项分布的共轭分布,因此狄利克雷分布常作为多项分布的先验分布使用,它是多项分布似然的共轭先验。
狄利克雷分布本质上是多元连续型随机变量的概率密度分布,假设多元随机变量 θ = ( θ 1 , θ 2 , . . . , θ k ) θ=(θ_1,θ_2,...,θ_k) θ=(θ1,θ2,...,θk) 服从参数 α = ( α 1 , α 2 , . . . , α k ) \alpha=(\alpha _1,\alpha _2,...,\alpha _k) α=(α1,α2,...,αk) 的狄利克雷分布,记作 θ ∽ D i r ( α ) θ \backsim Dir(\alpha) θ∽Dir(α) ,则概率密度函数可表示为:
p ( θ ∣ α ) = Γ ( ∑ i = 1 k α i ) ∏ i = 1 k Γ ( α i ) ∏ i = 1 k θ i α i − 1 = 1 B ( α ) ∏ i = 1 k θ i α i − 1 ( 1 ) p(θ|\alpha)={\Gamma(\sum_{i=1}^k{\alpha _i})\over{\prod_{i_=1}^k\Gamma(\alpha _i)}}\prod_{i=1}^k θ_i^{\alpha_{i-1}}={1\over{B(\alpha)}}\prod_{i=1}^k θ_i^{\alpha_{i-1}} \ \ \ \ \ (1) p(θ∣α)=∏i=1kΓ(αi)Γ(∑i=1kαi)∏i=1kθiαi−1=B(α)1∏i=1kθiαi−1 (1)
其中, ∑ i = 1 k θ i = 1 \sum_{i=1}^kθ_i=1 ∑i=1kθi=1 , θ i ≥ 0 θ_i \geq 0 θi≥0 , α i > 0 \alpha_i > 0 αi>0
初识者对式 ( 1 ) (1) (1) 可能不明就里,我们来对它做个通俗的解释。
在二项分布和Beta分布中我们曾以抛硬币举例,因为他们只涉及到二元变量,硬币的正反面就可以表示。
在多项分布里面用的是骰子举例,狄利克雷分布也同样可以效仿之。
假设有个生产骰子的工厂,这个工厂技术精湛且先进,不仅能造出一般的质地均匀的六面骰子,甚至可以造出任意质地任意多个面的骰子,这里质地均匀指的是骰子掷出每个面的概率相同,任意质地指掷出每个面的概率不同(但和为1)。在此背景下,狄利克雷分布中的 k k k 元随机变量 θ = ( θ 1 , θ 2 , . . . , θ k ) θ=(θ_1,θ_2,...,θ_k) θ=(θ1,θ2,...,θk) 可以看作掷一枚这个工厂生产的具有 k k k 个面的骰子时, 每个面出现的概率;参数 α = ( α 1 , α 2 , . . . , α k ) \alpha=(\alpha _1,\alpha _2,...,\alpha _k) α=(α1,α2,...,αk) 可以看作掷 n n n 次骰子中, k k k 个面中每个面出现的次数,并且满足 ∑ i = 1 k θ i = 1 \sum_{i=1}^kθ_i=1 ∑i=1kθi=1 , ∑ i = 1 k α i = n \sum_{i=1}^k\alpha_i=n ∑i=1kαi=n 。
因为 θ θ θ 满足 ∑ i = 1 k θ i = 1 \sum_{i=1}^kθ_i=1 ∑i=1kθi=1 , θ i ≥ 0 θ_i \geq 0 θi≥0 ,可以说狄利克雷分布的 k k k 元随机变量 θ = ( θ 1 , θ 2 , . . . , θ k ) θ=(θ_1,θ_2,...,θ_k) θ=(θ1,θ2,...,θk) 是定义在 k − 1 k-1 k−1 维概率单纯形(K-dimentional probability simplex)上的 。 k k k 维单纯形就是具有 k + 1 k+1 k+1 个顶点的凸多面体,比如二维单纯形是个三角形、有三个顶点;三维单纯形是四面体、有四个顶点。 k k k 表示类别的数量,概率单纯形上的一个点可以用 k k k 个和为1的非负数表示。比如当 k = 3 k=3 k=3 时, θ 1 、 θ 2 、 θ 3 θ_1、θ_2、θ_3 θ1、θ2、θ3 分布在三维空间 z = 1 − x − y z=1-x-y z=1−x−y 的平面三角形上,是个二维单纯形。

相关文章:

【机器学习前置知识】狄利克雷分布
在阅读本文前,建议先食用以下几篇文章以能更好地理解狄利克雷分布: 二项分布 Beta分布 多项分布 共轭分布 狄利克雷分布 狄利克雷分布(Dirichlet distribution)是Beta分布的扩展,把Beta分布从二元扩展到多元形式就是狄利克雷分布&#…...
)
Spring Retry(方法重试、方法重新调用)
Spring Retry——方法重试、方法重新调用 简介:使用1. 配置2.使用 总结注意 简介: Spring Retry 是一个 Spring Boot 官方提供的支持重试机制的库。它提供了一种简单而灵活的方式来处理方法调用可能失败的情况,通过自动重试失败的操作&#…...

JavaScript音视频,使用JavaScript如何在浏览器录制电脑摄像头画面为MP4视频文件并下载视频文件到本地
前言 本章介绍使用JavaScript如何在浏览器录制电脑摄像头画面为MP4视频文件并下载视频文件到本地。 实现功能 1、使用navigator.mediaDevices.getUserMedia获取摄像头画面 2、将获取到的摄像头画面渲染到canvas画板上 3、将canvas转换为blob对象 4、通过document.createElem…...

IaC基础设施即代码:使用Terraform 连接 alicloud阿里云
目录 一、实验 1.环境 2.alicloud阿里云创建用户 3.Linux使用Terraform 连接 alicloud 4.Windows使用Terraform 连接 alicloud 二、问题 1.Windows如何申明RAM 相关变量 2.Linux如何申明RAM 相关变量 3. Linux terraform 初始化失败 4.Linux terraform 计划与预览失败…...

Vue3 如何使用移动端调试工具vConsole
1、安装 pnpm i vconsole2、在src/utils下新建vconsole.ts,写入以下代码 // 这是移动端控制台调试工具,需要调试就打开,不用就注释 import vConsole from vconsole const vconsole new vConsole()3、src/main.ts 引入,需要调试就打开,&…...

【物流管理系统-Python简易版】
前端设计-后端开发(DJango项目Demo) 参考资料:【一文到底】【0基础】【快速上手】Django基本使用 创建项目 Pycharm专业版新建DJango项目 项目文件介绍: django_study_demo │─ manage.py 【项目管理的脚本,不要修…...

Vue学习笔记六--Vue3学习
1、Vue3的优势 2、创建Vue3工程 前提:node -v 查看node版本,需要在16.0及以上 创建命令 npm init vuelatest,先安装create-vue然后创建项目 然后执行npm run dev 提示 sh: vite: command not found,需要执行npm i重新安装依赖,之后再执行np…...

21.在线与离线MC强化学习简介
文章目录 1. 什么是在线MC强化学习2. 什么是离线MC强化学习3. 在线MC强化学习有何缺点 1. 什么是在线MC强化学习 在线强化学习(on-policy MC RL),是指:智能体在策略评估时为获取完整轨迹所采用的采样策略 π s a m p l e ( a ∣ …...

控制网页的灰度显示
1.代码: 普通网页 <style>html {filter: grayscale(100%);}</style> 或是:webkit内核浏览器写法 <style>html {-webkit-filter: grayscale(100%)}</style> 2.说明: grayscale(amount) :进行灰度转换。 amount转换值的大小&…...
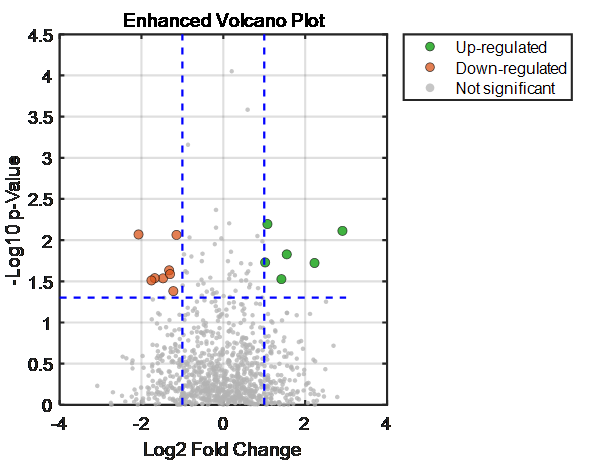
科研绘图(四)火山图
火山图是生物信息学中常用的一种图表,用来显示基因表达数据的变化。它通常将每个点表示为一个基因,x轴显示对数比率(log ratio),表示基因表达的变化大小;y轴显示-log10(p-value),表示变化的统计…...
超强站群系统v9.0:最新蜘蛛池优化技术,一键安装,内容无缓存刷新,高效安全
安全、高效,化的优化利用php性能,使得运行流畅稳定 独创内容无缓存刷新不变,节省硬盘。防止搜索引擎识别蜘蛛池 蜘蛛池算法,轻松构建站点(电影、资讯、图片、论坛等等) 可以个性化每个网站的风格、内容、…...

torch.fx的极简通用量化教程模板
现在比较流行的方式,是使用 torch.fx来做量化,比如地平线J3/J5的oe开发包中内嵌的ptq/qat量化方式,就是基于torch.fix进行开发的。本文将使用100行代码教你入门比较标准的量化步骤。,这些问题需要解答。本文100行代码,麻雀虽小五脏俱全,包括怎么用,用在哪里,哪里不能用…...
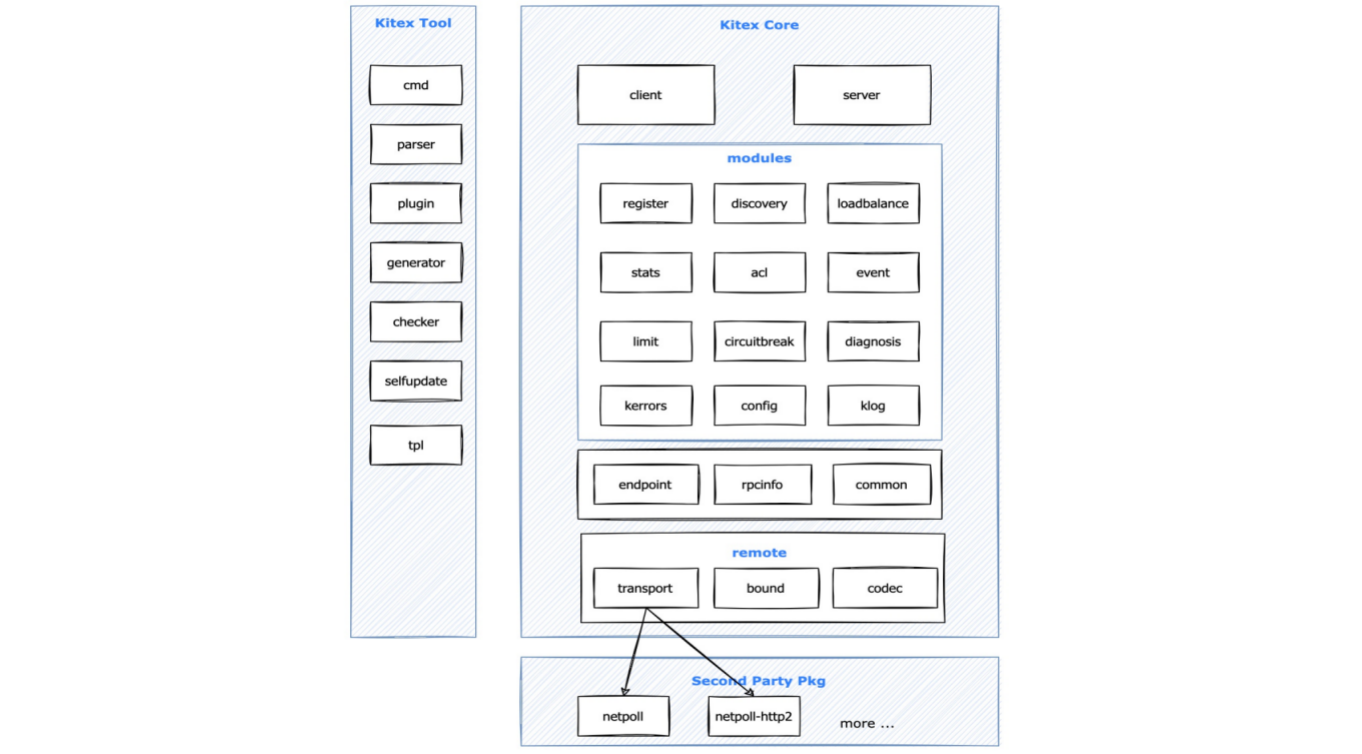
rpc的正确打开方式|读懂Go原生net/rpc包
前言 大家好,这里是白泽,之前最近在阅读字节跳动开源RPC框架Kitex的源码,分析了如何借助命令行,由一个IDL文件,生成client和server的脚手架代码,也分析了Kitex的日志组件klog。当然Kitex还有许多其他组件&…...

【信号与系统】【北京航空航天大学】实验二、连续时间系统的时域分析【MATLAB】
一、实验目的 1、掌握连续时间信号的卷积运算以及其对应的 MATLAB 实现方法; 2、掌握连续系统的冲激响应、阶跃响应 以及其对应的 MATLAB 实现方法; 3、掌握利用 MATLAB 求 LTI (Linear Time-Invariant, 线性时不变)系统响应的方…...
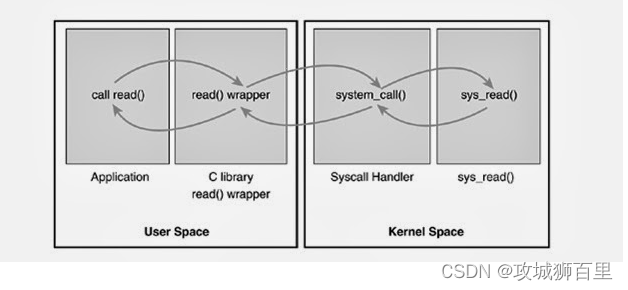
【Linux 内核源码分析笔记】系统调用
在Linux内核中,系统调用是用户空间程序与内核之间的接口,它允许用户空间程序请求内核执行特权操作或访问受保护的内核资源。系统调用提供了一种安全可控的方式,使用户程序能够利用内核功能而不直接访问底层硬件。 系统调用: 通过…...

mysql清空并重置自动递增初始值
需求:当上新项目时,测试环境数据库导出来的表id字段一般都有很大的初始递增值了,需要重置一下 先上代码: -- 查看当前自动递增值 SHOW CREATE TABLE table_name; -- 重建自动递增索引(可选) ALTER TABLE t…...

计算机算法之二分算法
文章目录 前言核心问题遍历查找思路遍历查找代码实现遍历查找缺点二分查找思路二分查找代码实现二分查找优点二分查找的变种问题一解题思路代码实现问题二解题思路代码实现 前言 大家好,我是醉墨居士,今天聊一下计算机中的经典算法 - 二分算法 核心问题…...
获取当前设备的IP
背景: 在本地使用自带webUI的项目时,需要制定webUI的访问地址。 一般本地访问使用:127.0.0.1,配置为可以从其他设备访问时,需要指定当前设备的IP,或者指定为0.0.0.0。 例如:使用locust的时候&a…...

koa2文件的上传下载功能
const Router require(“koa-router”); const upload new Router(); const bodyParser require(“koa-bodyparser”); const multer require("koa/multer"); const path require(“path”); const article require("…/utils/sql"); const { getCur…...

test-02-test case generate 测试用例生成 EvoSuite 介绍
拓展阅读 junit5 系列 基于 junit5 实现 junitperf 源码分析 Auto generate mock data for java test.(便于 Java 测试自动生成对象信息) Junit performance rely on junit5 and jdk8.(java 性能测试框架。性能测试。压测。测试报告生成。) 拓展阅读 自动生成测试用例 什么…...

用docker来安装部署freeswitch记录
今天刚才测试一个callcenter的项目,所以尝试安装freeswitch 1、使用轩辕镜像 - 中国开发者首选的专业 Docker 镜像加速服务平台 编辑下面/etc/docker/daemon.json文件为 {"registry-mirrors": ["https://docker.xuanyuan.me"] }同时可以进入轩…...

laravel8+vue3.0+element-plus搭建方法
创建 laravel8 项目 composer create-project --prefer-dist laravel/laravel laravel8 8.* 安装 laravel/ui composer require laravel/ui 修改 package.json 文件 "devDependencies": {"vue/compiler-sfc": "^3.0.7","axios": …...

人工智能--安全大模型训练计划:基于Fine-tuning + LLM Agent
安全大模型训练计划:基于Fine-tuning LLM Agent 1. 构建高质量安全数据集 目标:为安全大模型创建高质量、去偏、符合伦理的训练数据集,涵盖安全相关任务(如有害内容检测、隐私保护、道德推理等)。 1.1 数据收集 描…...

pikachu靶场通关笔记19 SQL注入02-字符型注入(GET)
目录 一、SQL注入 二、字符型SQL注入 三、字符型注入与数字型注入 四、源码分析 五、渗透实战 1、渗透准备 2、SQL注入探测 (1)输入单引号 (2)万能注入语句 3、获取回显列orderby 4、获取数据库名database 5、获取表名…...

Ubuntu Cursor升级成v1.0
0. 当前版本低 使用当前 Cursor v0.50时 GitHub Copilot Chat 打不开,快捷键也不好用,当看到 Cursor 升级后,还是蛮高兴的 1. 下载 Cursor 下载地址:https://www.cursor.com/cn/downloads 点击下载 Linux (x64) ,…...

API网关Kong的鉴权与限流:高并发场景下的核心实践
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 引言 在微服务架构中,API网关承担着流量调度、安全防护和协议转换的核心职责。作为云原生时代的代表性网关,Kong凭借其插件化架构…...

【Linux】Linux安装并配置RabbitMQ
目录 1. 安装 Erlang 2. 安装 RabbitMQ 2.1.添加 RabbitMQ 仓库 2.2.安装 RabbitMQ 3.配置 3.1.启动和管理服务 4. 访问管理界面 5.安装问题 6.修改密码 7.修改端口 7.1.找到文件 7.2.修改文件 1. 安装 Erlang 由于 RabbitMQ 是用 Erlang 编写的,需要先安…...

【Kafka】Kafka从入门到实战:构建高吞吐量分布式消息系统
Kafka从入门到实战:构建高吞吐量分布式消息系统 一、Kafka概述 Apache Kafka是一个分布式流处理平台,最初由LinkedIn开发,后成为Apache顶级项目。它被设计用于高吞吐量、低延迟的消息处理,能够处理来自多个生产者的海量数据,并将这些数据实时传递给消费者。 Kafka核心特…...

2025年- H71-Lc179--39.组合总和(回溯,组合)--Java版
1.题目描述 2.思路 当前的元素可以重复使用。 (1)确定回溯算法函数的参数和返回值(一般是void类型) (2)因为是用递归实现的,所以我们要确定终止条件 (3)单层搜索逻辑 二…...

CTF show 数学不及格
拿到题目先查一下壳,看一下信息 发现是一个ELF文件,64位的 用IDA Pro 64 打开这个文件 然后点击F5进行伪代码转换 可以看到有五个if判断,第一个argc ! 5这个判断并没有起太大作用,主要是下面四个if判断 根据题目…...
