回环检测算法:Stable Trangle Descriptor
回环检测是指检测传感器的两次测量(如图像、激光雷达扫描)是否发生在同一场景,它是对于SLAM问题至关重要。基于激光雷达的回环检测应该满足如下要求:
- 无论视点如何变化,回环检测方法应该实现旋转和平移不变性;
- 回环检测方法对不同的点云密度和环境应具有鲁棒性,因为激光扫描点云的稀疏性随距离、场景和激光雷达类型而变化;
- 回环检测算法能够更好的提供两帧激光扫描之间的相对位姿,一个好的初始值能让后续的配准算法收敛的更快更准确。
STD-LCD可以高效地检测闭环,并提供可靠的闭环几何变换。此外,它可以处理小重叠回环检测的挑战情况。与其他描述符中使用的多边形相比,三角形更稳定,因为三角形的形状是给定边长(或夹角)唯一确定的。此外,三角形的形状对于刚性变换是完全不变的。与关键点附近的的局部描述符相比,三角形的形状是旋转和平移不变的。基于这一性质,STD设计了一种算法,从三维点云中高效地提取局部关键点,并将这些关键点编码为三角形描述符。然后,通过匹配点云之间描述符的边长(和一些其他信息)来实现回环检测。从描述符匹配得到的点对关系可以进一步用于几何验证,这大大提高了回环检测的准确率。
关键点提取和描述符构建
当接收到累积子图后,STD-LCD对子图进行体素化,对体素中的点 p i ( i = 1 , … , N ) \mathbf{p}_i(i=1,\ldots,N) pi(i=1,…,N)求协方差矩 Σ \bm \Sigma Σ。
p ˉ = 1 N ∑ i = 1 N p i ; Σ = 1 N ( p i − p ˉ ) ( p i − p ˉ ) T \bar{\mathbf{p}}=\frac{1}{N}\sum_{i=1}^{N}\mathbf{p}_i;\quad\boldsymbol{\Sigma}=\frac{1}{N}(\mathbf{p}_i-\bar{\mathbf{p}})(\mathbf{p}_i-\bar{\mathbf{p}})^T pˉ=N1i=1∑Npi;Σ=N1(pi−pˉ)(pi−pˉ)T
令 λ k \lambda_k λk为 Σ \bm{\Sigma} Σ第 k k k大特征值,平面判定准则为 λ 3 < σ 1 , λ 2 > σ 2 \lambda_3<\sigma_1,\lambda_2>\sigma_2 λ3<σ1,λ2>σ2,其中 σ 1 \sigma_1 σ1和 σ 2 \sigma_2 σ2是预设超参数,一般 σ 1 \sigma_1 σ1为一个较小的值, σ 2 \sigma_2 σ2为一个较大的值。将满足平面判定准则的体素定义为平面体素,否则为非平面体素。
通过区域生长的方法将平面体素合并为更大的平面,即从一个随机的平面体素开始,如果其相邻体素有相同的平面法向量且平面距离小于阈值,则将其加入到当前正在生长的平面中。否则,如果相邻体素并不在同一平面上,则将其加入到当前正在生长的平面的边界体素表中。重复以上操作直到所有添加进来的体素都已经被扩展或者达到边界体素。
以生长得到的平面为图像平面,将边界体素的点投影到相邻平面上,以边界体素中的点到平面的最大距离为像素值。对于图像,将具有局部最大点到平面距离的像素中距离最大的点设置为关键点。将提取到的关键点构建成一个kd树,并对每一个关键点搜索其最近邻的20个关键点构建三角描述符。进行空间非极大值抑制,将具有相同边长的描述符去重,以增强提取的非重复性。
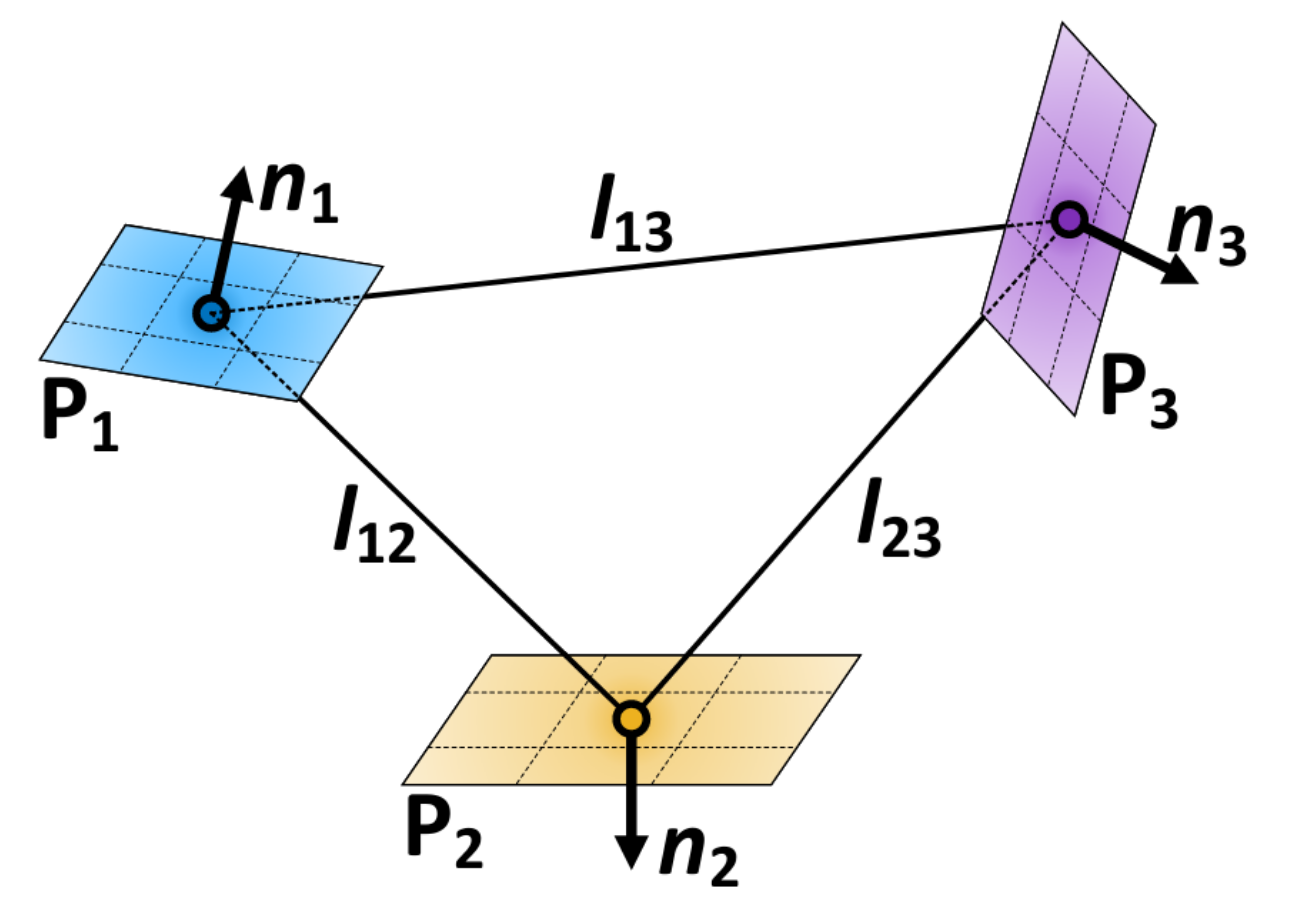
每个三角形描述符 Δ \bm{\Delta} Δ包含的元素如下
- 三个顶点 p 1 , p 2 , p 3 \mathbf{p}_1,\mathbf{p}_2,\mathbf{p}_3 p1,p2,p3,
- 三个对应投影平面的法向量 n 1 , n 2 , n 3 \mathbf{n}_1,\mathbf{n}_2,\mathbf{n}_3 n1,n2,n3,
- 三个边长 l 12 , l 23 , l 13 l_{12},l_{23},l_{13} l12,l23,l13且 l 12 ≤ l 23 ≤ l 13 l_{12}\leq l_{23}\leq l_{13} l12≤l23≤l13
- 三角形的中心 q \mathbf{q} q
- 描述符所属的关键帧索引 k k k
除了描述符,我们还将保存从这个子图中提取的所有 n n n个平面 Π = ( π 1 , π 2 , … , π n ) \bm \Pi = (\bm \pi_1,\bm \pi_2,\ldots,\bm \pi_n) Π=(π1,π2,…,πn),用于之后的几何验证步骤。
回环检测与验证
回环检测与验证包括三部分:粗回环检测、细回环检测和几何验证。粗循环检测通过在描述符数据库的哈希表中搜索匹配的历史描述符,可以快速地提取出N个可能的候选。精细回环检测通过计算配对三角形之间的所有变换矩阵,并对变换进行聚类,将包含变换数最多的聚类簇的中心作为优秀候选。最后,计算当前帧到优秀候选者的平面重合度筛选误检,选择点到平面距离最小的候选作为最佳候选。由于精细回环检测提供了一个较好的初始猜测,使得之后的ICP配准更快收敛。
由于一个子图可以提取上百个描述符,为了快速查询和匹配描述符,我们使用哈希表存储所有描述符。我们使用描述子中具有旋转和平移不变性的6个属性来计算哈希密钥,分别为边长 l 12 , l 23 , l 13 l_{12},l_{23},l_{13} l12,l23,l13和投影法向量的点积 n 1 ⋅ n 2 , n 2 ⋅ n 3 , n 1 ⋅ n 3 \mathbf{n}_1\cdot\mathbf{n}_2,\mathbf{n}_2\cdot\mathbf{n}_3,\mathbf{n}_1\cdot\mathbf{n}_3 n1⋅n2,n2⋅n3,n1⋅n3。具有6个相似属性的描述符将具有相同的哈希密钥,因此存储在同一个容器中。对于一个查询帧,我们提取其所有描述符。对于每个描述符 Δ i \bm{\Delta}_i Δi,计算其哈希密钥,将其定位到哈希表中对应的容器中,并对该容器中存在的所有描述符的关键帧进行投票。当查询帧中的所有描述符 Δ i \bm \Delta_i Δi都被处理后,匹配过程结束。投票数前十多的关键帧将被选为描述符的候选关键帧,用于回环检测。
当给定一个候选回环关键帧时,我们进行几何验证以消除由于描述符匹配不正确而导致的误检。由于边长确定后三角形的形状是唯一确定的,一旦 Δ a \bm\Delta_a Δa匹配到 Δ b \bm\Delta_b Δb,它们的顶点 ( p a 1 , p a 2 , p a 3 ) (\mathbf{p}_{a1},\mathbf{p}_{a2},\mathbf{p}_{a3}) (pa1,pa2,pa3)和 ( p b 1 , p b 2 , p b 3 ) (\mathbf{p}_{b1},\mathbf{p}_{b2},\mathbf{p}_{b3}) (pb1,pb2,pb3)将自然匹配。然后利用这个对应关系,根据\ref{pt2ptICP}节,通过奇异值分解(Singular Value Decomposition,SVD)很容易计算出这两个关键帧之间的相对变换 T = ( R , t ) \boldsymbol{T}=(\boldsymbol{R},\boldsymbol{t}) T=(R,t):
W = ∑ i = 1 3 ( p a i − q a ) ( p b i − q b ) [ U , S , V ] = S V D ( W ) R = V U T , t = − R ∗ q a + q b . \begin{aligned} &\mathbf{W}=\sum_{i=1}^3(\mathbf{p}_{a_i}-\mathbf{q}_a)(\mathbf{p}_{b_i}-\mathbf{q}_b) \\ &[\mathbf{U},\mathbf{S},\mathbf{V}]=\mathbf{SVD}(\mathbf{W}) \\ &\bm{R}=\mathbf{V}\mathbf{U}^T,\bm{t}=-\bm{R}*\mathbf{q}_a+\mathbf{q}_b. \end{aligned} W=i=1∑3(pai−qa)(pbi−qb)[U,S,V]=SVD(W)R=VUT,t=−R∗qa+qb.
为了增加鲁棒性,使用RANSAC方法来寻找最大化正确匹配描述符数量的刚体变换。
基于此刚体变换,我们计算当前帧与候选帧之间的平面重叠度来进行几何验证。
用中心点 q \mathbf{q} q和法向量 u \mathbf{u} u 表示的平面 π \bm\pi π。记当前帧的平面集为 B Π = [ ( B q 1 , B u 1 ) , … ( B q n , B u n ) ] ^{B}\Pi = [(^{B}\mathbf{q}_1,{}^{B}\mathbf{u}_1),\ldots(^{B}\mathbf{q}_n,{}^{B}\mathbf{u}_n)] BΠ=[(Bq1,Bu1),…(Bqn,Bun)],候选帧的平面集为 C Π = [ ( C q 1 , C u 1 ) , … ( C q n , C u n ) ] ^{C}\Pi = [(^{C}\mathbf{q}_1,{}^{C}\mathbf{u}_1),\ldots(^{C}\mathbf{q}_n,{}^{C}\mathbf{u}_n)] CΠ=[(Cq1,Cu1),…(Cqn,Cun)],刚体变换为 C T B = ( C R B , C t B ) ∈ S E ( 3 ) {}^{C}\bm{T}_B= ( {}^C\bm{R}_B,{}^C\bm{t}_B)\in SE(3) CTB=(CRB,CtB)∈SE(3),其中 n n n为当前帧的平面数, m m m为候选框的平面数。我们以 C Π {}^C\Pi CΠ的中心点 ( C q 1 , C q 2 , … , C q m ) ({}^C\mathbf{q}_1,{}^C\mathbf{q}_2,\ldots,{}^C\mathbf{q}_m) (Cq1,Cq2,…,Cqm)构建一个kd树(k=3)。则对于每个平面中心点 B q i ( i = 1 , 2 , … , n ) ∈ B Π {}^B\mathbf{q}_i(i=1,2,\ldots,n)\in{}^B\Pi Bqi(i=1,2,…,n)∈BΠ,首先用 C T B {}^C\mathbf{T}_B CTB对 B q i {}^B\mathbf{q}_i Bqi进行变换,然后在kd树中搜索一个最近的点 C q j {}^C\mathbf{q}_j Cqj,通过法向量差和点到平面的距离判断两个平面是否重合:
∥ C R B B u i − C u j ∥ 2 < σ n C u j T ( C T B B q i − C q j ) < σ d \begin{aligned} \|{}^C\bm{R}_B{}^B\mathbf{u}_i-{}^C\mathbf{u}_j\|_2<\sigma_n \\[0.3em] {}^C\mathbf{u}_j^T(^C\bm{T}_B{}^B\mathbf{q}_i-{}^C\mathbf{q}_j)<\sigma_d \end{aligned} ∥CRBBui−Cuj∥2<σnCujT(CTBBqi−Cqj)<σd
其中 σ n \sigma_n σn和 σ d \sigma_d σd是用来判断平面重合的预设参数。
计算当前帧满足式\ref{plane_overlap}的平面占所有平面的比例:
N c = N coincide N sum × 100 % , N_c=\frac{N_{\textsf{coincide}}}{N_{\textsf{sum}}}\times100\%, Nc=NsumNcoincide×100%,
其中 N coincide N_{\textsf{coincide}} Ncoincide为当前帧所有满足约束的平面数, N sum N_{\textsf{sum}} Nsum为当前帧所有平面的数量。
如果 N c N_c Nc超过阈值 σ p c \sigma_{pc} σpc,我们就认为这是一个可靠的回环检测。由于平面的数量远远少于点云的数量,基于平面的几何验证比基于ICP的验证方法效率更高。按照式\ref{STD-ICP}优化点面距离和法向量差异可以得到回环的精确刚体变换。
min C T B ∥ C R B B u i − C u j ∥ 2 2 + ( C u j T ( C T B B q i − C q j ) ) 2 \min_{^C\bm{T}_B}\|{}^C\bm{R}_B{}^B\mathbf{u}_i-{}^C\mathbf{u}_j\|_2^2+\left({}^C\mathbf{u}_j^T(^C\bm{T}_B{}^B\mathbf{q}_i-{}^C\mathbf{q}_j)\right)^2 CTBmin∥CRBBui−Cuj∥22+(CujT(CTBBqi−Cqj))2
STD-LCD回环检测通过求解如式所示的优化问题可以直接得到查询帧 i i i与回环帧 j j j之间的相对位姿约束 Δ T i j \Delta \mathbf{T}_{ij} ΔTij,构造回环因子并加入到因子图中:
F L = ∑ ( i , j ) ∈ L ∥ L o g ( Δ T i j − 1 ( X i − 1 X j ) ) ∥ Σ L i j 2 F_{\mathcal{L}} = \sum_{{(i,j)}\in\mathcal{L}}\left\|\mathrm{Log}\left(\Delta \mathbf{T}_{ij}^{-1} \left({\bm{X}_{i}^{-1} }\bm{X}_{j}\right)\right)\right\|^2_{\bm \Sigma_{\mathcal{L}_{ij}}} FL=(i,j)∈L∑ Log(ΔTij−1(Xi−1Xj)) ΣLij2
其中 X i \bm{X}_{i} Xi为查询帧全局位姿变量, X j \bm{X}_{j} Xj为回环帧全局位姿变量, Σ L i j \Sigma_{\mathcal{L}_{ij}} ΣLij为对应的信息矩阵, L \mathcal{L} L为回环约束帧索引集合。
相关文章:

回环检测算法:Stable Trangle Descriptor
回环检测是指检测传感器的两次测量(如图像、激光雷达扫描)是否发生在同一场景,它是对于SLAM问题至关重要。基于激光雷达的回环检测应该满足如下要求: 无论视点如何变化,回环检测方法应该实现旋转和平移不变性…...
MetaGPT入门(二)
接着MetaGPT入门(一),在文件里再添加一个role类 class SimpleCoder(Role):def __init__(self,name:str"Alice",profile:str"SimpleCoder",**kwargs):super().__init__(name,profile,**kwargs)self._init_actions([Write…...
AI嵌入式K210项目(4)-FPIOA
文章目录 前言一、FPIOA是什么?二、FPIOA代码分析总结 前言 磨刀不误砍柴工,在正式开始学习之前,我们先来了解下K210自带的FPIOA,这个概念可能与我们之前学习STM32有很多不同,STM32每个引脚都有特定的功能,…...
FPGA开发设计
一、概述 FPGA是可编程逻辑器件的一种,本质上是一种高密度可编程逻辑器件。 FPGA的灵活性高、开发周期短、并行性高、具备可重构特性,是一种广泛应用的半定制电路。 FPGA的原理 采用基于SRAM工艺的查位表结构(LUT),…...
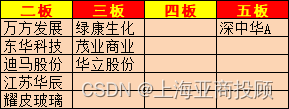
上海亚商投顾:沪指冲高回落 旅游板块全天强势
上海亚商投顾前言:无惧大盘涨跌,解密龙虎榜资金,跟踪一线游资和机构资金动向,识别短期热点和强势个股。 一.市场情绪 沪指昨日冲高回落,创业板指跌近1%,北证50指数跌超3%。旅游、零售板块全天强势…...
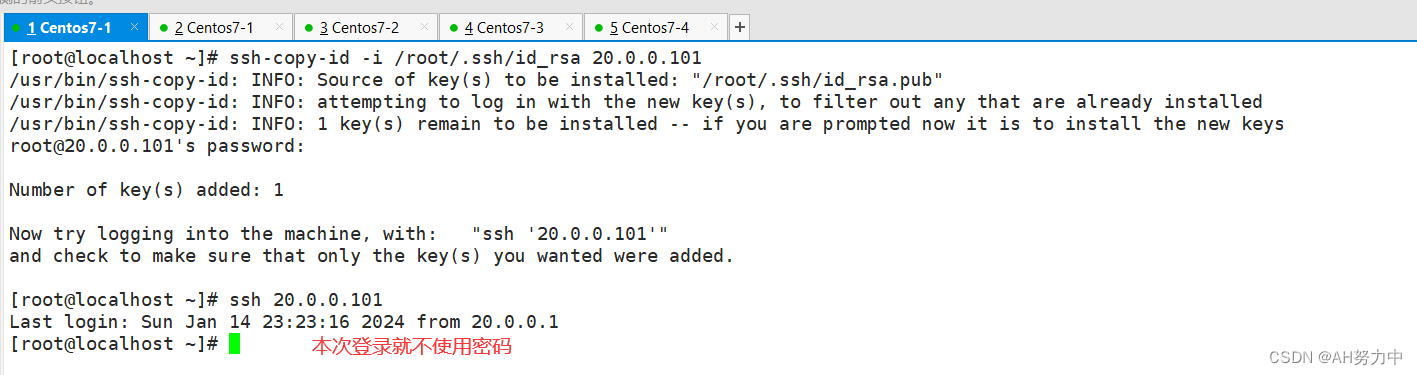
Linux网络--- SSH服务
一、ssh服务简介 1、什么是ssh SSH(Secure Shell)是一种安全通道协议,主要用来实现字符界面的远程登录、远程复制等功能。SSH 协议对通信双方的数据传输进行了加密处理,其中包括用户登录时输入的用户口令,SSH 为建立在…...

2.1 数组
2.1 数组 (1) 概述 定义 在计算机科学中,数组是由一组元素(值或变量)组成的数据结构,每个元素有至少一个索引或键来标识 因为数组内的元素是连续存储的,所以数组中元素的地址,可以通过其索引…...
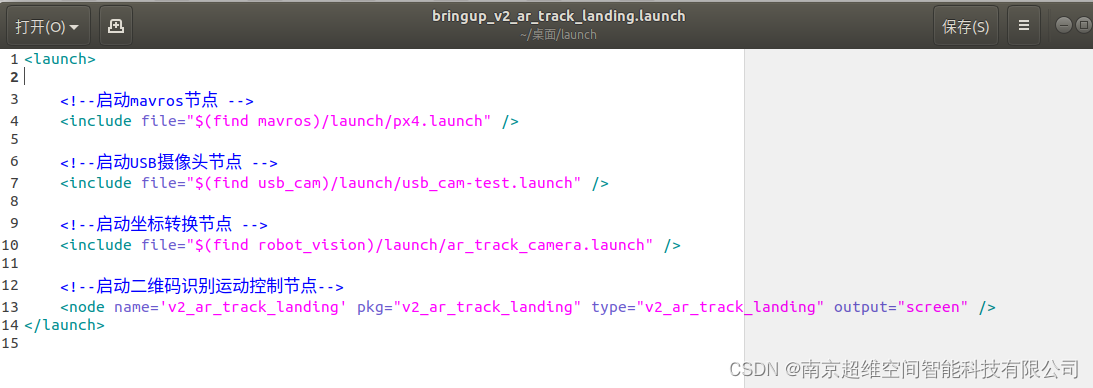
超维空间M1无人机使用说明书——53、ROS无人机二维码识别与降落——V2升级版本
引言:使用二维码引导无人机实现精准降落,首先需要实现对二维码的识别和定位,可以参考博客的二维码识别和定位内容。本小节主要是通过获取拿到的二维码位置,控制无人机全向的移动和降落,本小节再V1版本的基础上增加了动…...

瑞萨IDE:CS+ for CC进行BootLoader升级时开发环境配置
瑞萨IDE:CS+ for CC进行BootLoader升级时开发环境配置 2023-06-17 726 发布于河北 版权 简介: BootLoader程序设计是常用的嵌入式升级方案之一,通过使用UART、SPI、IIC等接口实现对嵌入式节点的远程升级。本片博文并不是讲解如何实现BootLoader升级程序,而是讲解使用CS+…...

翻译: Streamlit从入门到精通 显示图表Graphs 地图Map 主题Themes 二
Streamlit从入门到精通 系列: 翻译: Streamlit从入门到精通 基础控件 一 1. 使用Streamlit显示图表Graphs 1.1 为什么我们需要可视化? 数据可视化通过将数据整理成更容易理解的格式来讲述故事,凸显趋势和异常点。好的可视化能够讲述一个故…...
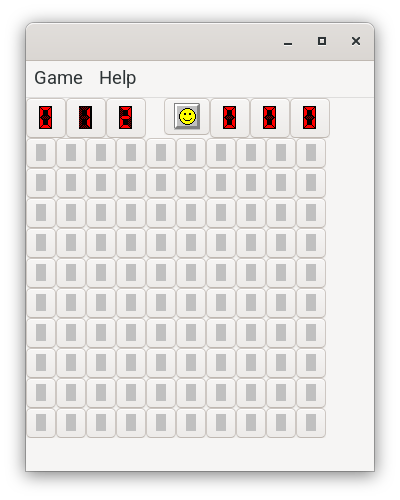
Java 开源扫雷游戏 JMine 发布新版 3.0 及介绍视频
Java 开源扫雷游戏 JMine 发布新版 3.0 及介绍视频 Java 开源扫雷游戏 JMine 是笔者开发的基于 Swing 的 Java 扫雷游戏,现已发布新版 3.0 及其介绍视频。视频请见: https://www.bilibili.com/video/BV1RK4y1z7Qz/ 老版本 JMine 1.2.5 的介绍视频请见…...
Vue v-model 详解
✨ 专栏介绍 在当今Web开发领域中,构建交互性强、可复用且易于维护的用户界面是至关重要的。而Vue.js作为一款现代化且流行的JavaScript框架,正是为了满足这些需求而诞生。它采用了MVVM架构模式,并通过数据驱动和组件化的方式,使…...

一个超级牛逼的消息推送系统Gotify 使用Gotify来搭建你的消息推送系统
目录 先看效果 简介 1.1创建目录 3.访问服务端 3.1示例 3.2创建应用 4.安装apk 4.1下载apk 4.2安装 4.3配置服务器地址 5.推送消息测试 5.1服务器执行 5.2手机端查看 支持删除 6.源码地址 先看效果 打开应用 简介 gotify 支持的功能如下 可以通过 restapi 发送消…...

【架构设计】单体软件向微服务化演变
单体软件 假设单体软件的各模块如下,其中服务包含许多功能模块,如用户管理模块、商品模块、订单模块、仓库模块; #mermaid-svg-MzWKwMCwfo3PWMGH {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-…...
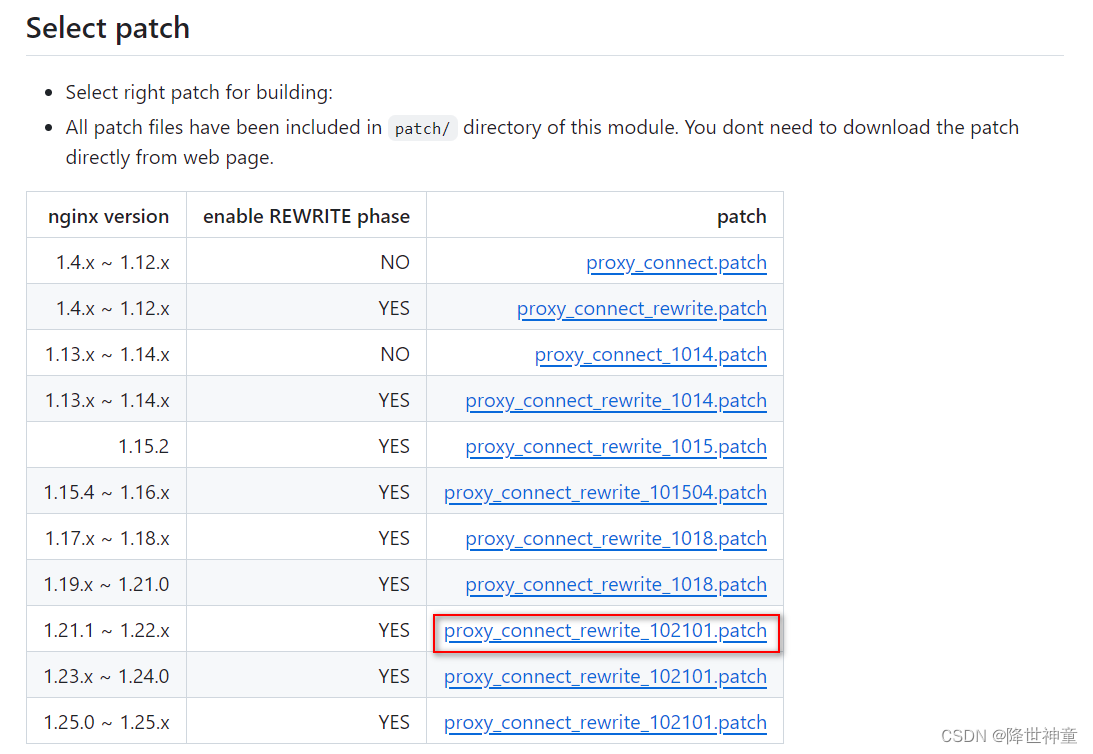
部署ATS(Apache Traffic Server)和Nginx正向代理服务性能对比
部署ATS(Apache Traffic Server)和Nginx正向代理服务&性能对比 1. 正向代理的用途2. ATS(Apache Traffic Server)正向代理服务器部署3. Nginx正向代理服务器部署4. 性能对比 1. 正向代理的用途 正向代理一般是用于内部网络出去,反向代理一…...

kafka入门(六):日志分段(LogSegment)
日志分段(LogSegment) Kafka的一个 主题可以分为多个分区。 一个分区可以有一至多个副本,每个副本对应一个日志文件。 每个日志文件对应一个至多个日志分段(LogSegment)。 每个日志分段还可以细分为索引文件、日志存储…...

Python 与 PySpark数据分析实战指南:解锁数据洞见
目录 前言 1. 数据准备 2. 数据探索 3. 数据可视化 4. 常见数据分析任务 ⭐️ 好书推荐 前言 前些天发现了一个巨牛的人工智能学习网站,通俗易懂,风趣幽默,忍不住分享一下给大家。 点击跳转到网站 数据分析是当今信息时代中至关重要的技…...
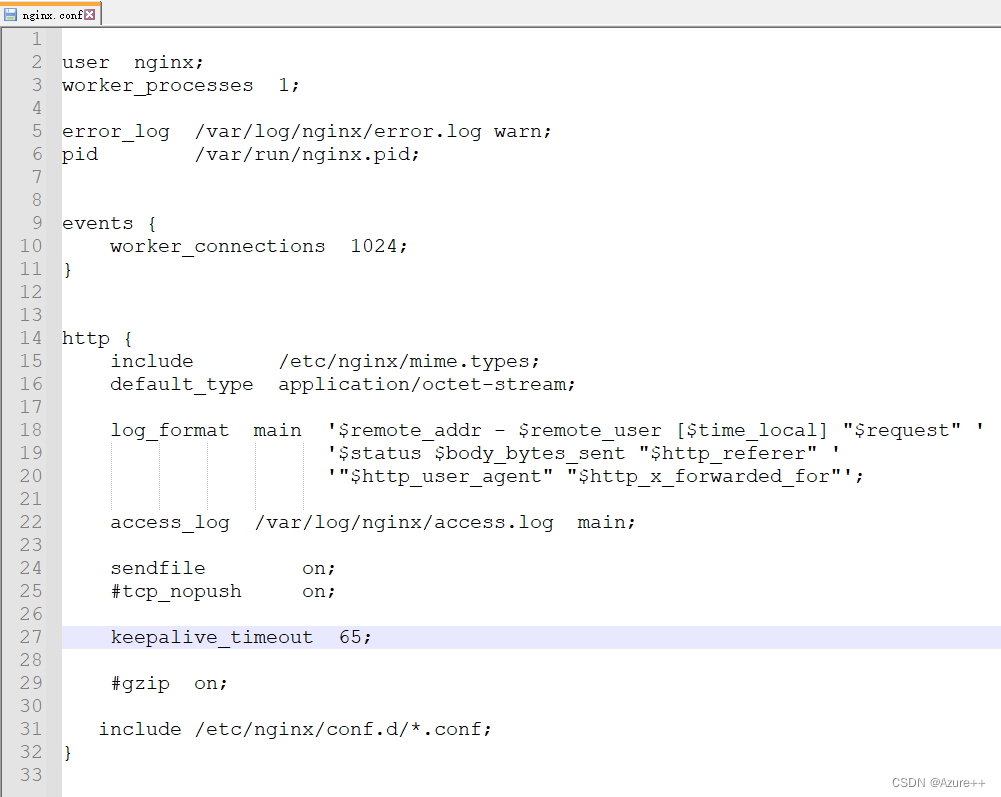
docker使用nginx部署vue刷新页面404
docker使用nginx部署vue刷新页面404 从docker内部复制出来的配置文件是这样的,但是刷新页面之后就显示404,关键是我两个前端项目都是用的这一个配置文件,但是只有一个项目出现刷新浏览器显示404的问题,这给我搞懵了!&…...

openGauss学习笔记-198 openGauss 数据库运维-常见故障定位案例-分析查询效率异常降低的问题
文章目录 openGauss学习笔记-198 openGauss 数据库运维-常见故障定位案例-分析查询效率异常降低的问题198.1 分析查询效率异常降低的问题198.1.1 问题现象198.1.2 处理办法 openGauss学习笔记-198 openGauss 数据库运维-常见故障定位案例-分析查询效率异常降低的问题 198.1 分…...
、List.clear()方法,清空时注意!)
使用Map.clear()、List.clear()方法,清空时注意!
对 Map、List 对象进行清空操作时,常常会使用 clear() 方法。 例如,清空 Map Map map new HashMap();map.put("key1","value1");map.put("key2","value2");System.out.println(map.size()); //2map.clear();Sy…...

IDEA运行Tomcat出现乱码问题解决汇总
最近正值期末周,有很多同学在写期末Java web作业时,运行tomcat出现乱码问题,经过多次解决与研究,我做了如下整理: 原因: IDEA本身编码与tomcat的编码与Windows编码不同导致,Windows 系统控制台…...

谷歌浏览器插件
项目中有时候会用到插件 sync-cookie-extension1.0.0:开发环境同步测试 cookie 至 localhost,便于本地请求服务携带 cookie 参考地址:https://juejin.cn/post/7139354571712757767 里面有源码下载下来,加在到扩展即可使用FeHelp…...

【kafka】Golang实现分布式Masscan任务调度系统
要求: 输出两个程序,一个命令行程序(命令行参数用flag)和一个服务端程序。 命令行程序支持通过命令行参数配置下发IP或IP段、端口、扫描带宽,然后将消息推送到kafka里面。 服务端程序: 从kafka消费者接收…...
:OpenBCI_GUI:从环境搭建到数据可视化(下))
脑机新手指南(八):OpenBCI_GUI:从环境搭建到数据可视化(下)
一、数据处理与分析实战 (一)实时滤波与参数调整 基础滤波操作 60Hz 工频滤波:勾选界面右侧 “60Hz” 复选框,可有效抑制电网干扰(适用于北美地区,欧洲用户可调整为 50Hz)。 平滑处理&…...
:にする)
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする 1、前言(1)情况说明(2)工程师的信仰2、知识点(1) にする1,接续:名词+にする2,接续:疑问词+にする3,(A)は(B)にする。(2)復習:(1)复习句子(2)ために & ように(3)そう(4)にする3、…...

安宝特方案丨XRSOP人员作业标准化管理平台:AR智慧点检验收套件
在选煤厂、化工厂、钢铁厂等过程生产型企业,其生产设备的运行效率和非计划停机对工业制造效益有较大影响。 随着企业自动化和智能化建设的推进,需提前预防假检、错检、漏检,推动智慧生产运维系统数据的流动和现场赋能应用。同时,…...

java 实现excel文件转pdf | 无水印 | 无限制
文章目录 目录 文章目录 前言 1.项目远程仓库配置 2.pom文件引入相关依赖 3.代码破解 二、Excel转PDF 1.代码实现 2.Aspose.License.xml 授权文件 总结 前言 java处理excel转pdf一直没找到什么好用的免费jar包工具,自己手写的难度,恐怕高级程序员花费一年的事件,也…...

pam_env.so模块配置解析
在PAM(Pluggable Authentication Modules)配置中, /etc/pam.d/su 文件相关配置含义如下: 配置解析 auth required pam_env.so1. 字段分解 字段值说明模块类型auth认证类模块,负责验证用户身份&am…...

基于数字孪生的水厂可视化平台建设:架构与实践
分享大纲: 1、数字孪生水厂可视化平台建设背景 2、数字孪生水厂可视化平台建设架构 3、数字孪生水厂可视化平台建设成效 近几年,数字孪生水厂的建设开展的如火如荼。作为提升水厂管理效率、优化资源的调度手段,基于数字孪生的水厂可视化平台的…...

uniapp微信小程序视频实时流+pc端预览方案
方案类型技术实现是否免费优点缺点适用场景延迟范围开发复杂度WebSocket图片帧定时拍照Base64传输✅ 完全免费无需服务器 纯前端实现高延迟高流量 帧率极低个人demo测试 超低频监控500ms-2s⭐⭐RTMP推流TRTC/即构SDK推流❌ 付费方案 (部分有免费额度&#x…...
