动态规划解决马尔可夫决策过程
马尔可夫决策过程是强化学习中的基本问题模型之一,而解决马尔可夫决策过程的方法我们统称为强化学习算法。
动态规划( dynamic programming, DP )具体指的是在某些复杂问题中,将问题转化为若干个子问题,并在求解每个子问题的过程中保存已经求解的结果,以便后续使用。
常见的动态规划算法包括
- 值迭代(value iteration, VI)
- 策略迭代(policy iteration, PI)
- Q-learning 算法等。
动态规划三个基本原理
- 最优化原理:问题的最优解所包含的子问题的解也是最优的,就称该问题具有最优子结构
- 无后效性:某阶段状态一旦确定,就不受这个状态以后决策的影响
- 重叠子问题:不是动态规划问题的必要条件
马尔可夫决策过程的目标是最大化累积回报
G t = R t + 1 + γ G t + 1 G_t = R_{t+1} + \gamma G_{t+1} Gt=Rt+1+γGt+1
我们要解决 G t + 1 G_{t+1} Gt+1的问题,可以一次拆分成解决 G t , G t − 1 , . . . , G 1 G_{t},G_{t-1},...,G_1 Gt,Gt−1,...,G1的问题,这其实就满足动态规划性质中的最优化原理
策略迭代与价值迭代
但如果只给定马尔可夫决策过程,该如何寻找最佳策略,从而得到最佳价值函数(optimal value function)
最佳价值函数:寻找一种策略 π \pi π使得每个状态的价值最大。即使得V最大的 π \pi π
V ∗ ( s ) = m a x π V π ( s ) V^*(s) = max_{\pi}V_{\pi}(s) V∗(s)=maxπVπ(s)
最佳策略下,每个状态的价值函数都为最大值,如果可以求得最佳价值函数,就认为该决策过程的环境可解,在可解环境下,最佳价值函数是一致的,但可以有多个策略达到最佳价值函数。换句话说,存在最优值,但解。
当得到最佳价值函数后,可以通过对Q函数最大化来得到最佳策略,使得Q函数最大化的动作就是最佳的动作,进而可以提取出最佳策略。
π ∗ ( a ∣ s ) = { 1 , a = a r g m a x a ∈ A Q ∗ ( s , a ) 0 , 其他 {\pi}^{*}(a|s) = \left\{ \begin{matrix} 1 , a = argmax{ \atop a \in A}Q^{*}(s,a)\\ 0,其他 \end{matrix} \right. π∗(a∣s)={1,a=argmaxa∈AQ∗(s,a)0,其他
Q:怎样进行策略搜索
方法一:穷举法,假设有S个状态,A个动作。总共 ∣ A ∣ ∣ S ∣ |A|^{|S|} ∣A∣∣S∣个策略。
方法二:策略迭代和价值迭代
策略迭代
策略迭代:包括策略评估和策略改进
策略评估:给定马尔可夫决策过程和策略,评估我们可以获得多少价值,即对于当前策略,我们可以得到多大的价值。
在下图左侧,先进行策略评估,即基于给定的策略 π \pi π,先求得价值函数V。然后基于奖励函数和状态转移函数可以计算得到Q函数。
Q π i ( s , a ) = R ( s , a ) + γ ∑ s ′ ∈ S p ( s ′ ∣ s , a ) V π i ( s ′ ) Q_{\pi_i}(s,a) = R(s,a) + \gamma\sum{ \atop s' \in S}p(s'|s,a)V_{\pi_i}(s') Qπi(s,a)=R(s,a)+γ∑s′∈Sp(s′∣s,a)Vπi(s′)
在下图右侧,随后进行策略改进,基于Q函数,取使得Q取最大值的动作,做为下一个策略。
π i + 1 ( s ) = a r g m a x a Q π i ( s , a ) \pi_{i+1}(s) = argmax_aQ_{\pi_i}(s,a) πi+1(s)=argmaxaQπi(s,a)

因此,可以将Q函数看做一个表格(Q-table),得到Q函数,也就得到Q表格。

对每一列,取使得Q函数最大的动作,即为最应该采取的动作。
通过argmax操作,我们会得到更好或者不变的策略,而不会使价值函数变差,当改进停止后会得到一个最佳策略。策略确定后,动作a确定,Q函数 Q ( s , a ) Q(s,a) Q(s,a)就会变为价值函数 V ( s ) V(s) V(s)
Q π ( s , π ′ ( s ) ) = max a ∈ A Q π ( s , a ) = Q π ( s , π ( s ) ) = V π ( s ) Q_{\pi}\left(s,\pi^{\prime}(s)\right)=\operatorname*{max}_{a\in A}Q_{\pi}(s,a)=Q_{\pi}(s,\pi(s))=V_{\pi}(s) Qπ(s,π′(s))=a∈AmaxQπ(s,a)=Qπ(s,π(s))=Vπ(s)
进而得到贝尔曼最优方程(Bellman optimality equation)
V π ( s ) = m a x a ∈ A Q π ( s , a ) V_{\pi}(s) = max_{a \in A}Q_{\pi}(s,a) Vπ(s)=maxa∈AQπ(s,a)
贝尔曼最优方程表明:最佳策略下的一个状态的价值必须等于在这个状态下采取最好动作得到的回报的期望。 当马尔可夫决策过程满足贝尔曼最优方程的时候,整个马尔可夫决策过程已经达到最佳的状态。
当整个状态已经收敛后,我们得到最佳价值函数后,贝尔曼最优方程才会满足。满足贝尔曼最优方程后,我们可以采用最大化操作,即。
公式 1 : V ∗ ( s ) = m a x a Q ∗ ( s , a ) 公式1:V^{*}(s) = max_{a}Q^{*}(s,a) 公式1:V∗(s)=maxaQ∗(s,a)
Q函数的贝尔曼方程如下:
公式 2 : Q π i ( s , a ) = R ( s , a ) + γ ∑ s ′ ∈ S p ( s ′ ∣ s , a ) V ∗ ( s ′ ) 公式2:Q_{\pi_i}(s,a) = R(s,a) + \gamma\sum{ \atop s' \in S}p(s'|s,a)V^{*}(s') 公式2:Qπi(s,a)=R(s,a)+γ∑s′∈Sp(s′∣s,a)V∗(s′)
将公式1代入公式2,即可得到Q函数之间的转移。将公式2代入公式1,即可得到价值函数之间的转移。

价值迭代
策略迭代比价值迭代更快地接近最优解

基本概念
-
有模型算法:状态转移概率已知,例如动态规划
-
免模型算法:大部分情况下对于智能体来说,环境是未知的,即状态转移概率未知
除了动态规划之外,基础的强化学习算法都是免模型的。
预测:免模型情况下,去近似环境的状态价值函数。主要目的是估计或计算环境中的某种期望值,比如状态价值函数 V ( s ) V(s) V(s)或动作价值函数 Q ( s , a ) Q(s,a) Q(s,a)。
控制:目标则是找到一个最优策略,该策略可以最大化期望的回报。换句话说,你不仅想知道按照某种策略你的预期得分是多少,还想知道如何选择动作以最大化这个得分。
控制问题通常涉及
- 策略评估(policy evaluation)
- 策略改进(policy improvement)
在实际应用中,预测和控制问题经常交织在一起。例如,在使用 Q-learning(一种免模型的控制算法)时,我们同时进行预测(更新 Q值)和控制(基于Q值选择动作)。之所以提到这两个概念,是因为很多时候我们不能一蹴而就解决好控制问题,而需要先解决预测问题,进而解决控制问题。
什么情况下MDP是已知的?即奖励函数R和状态转移函数P被提供给智能体时。
因此可以基于策略评估和策略改进来计算出最优策略和最优状态价值函数。

Model-free RL
背景:策略迭代和价值迭代需要用到MDP,但在现实生活中,MDP往往不已知,或者较复杂。下图是有模型方法。

Model-free 方法通过智能体与环境交互得到一系列轨迹,基于这些轨迹计算状态和策略。

蒙特卡罗

这里提供一种增量求均值的方法,现在时刻的均值可以和上一时刻的均值建立联系。这种方法可以应用到增量求状态价值函数V上。

Temporal-Difference,TD
结合了MC和DP的方法
- 免模型
- 通过bootstrapping可以从不完整回合中学习
- 可以在不完整的环境上学习
TD(0)
TD target: sample + bootstrapping

TD learning只往前走了一步就开始更新V,而MC需要走完一个轨迹
TD(n)
往前走n步再更新,通过步数来调整。当步数无穷大时,TD target变为MC target






最右下角是穷举法,TD在广度增加就变为了DP,在深度增加就变为了MC。
策略迭代分两步:
- 计算状态价值函数V
- 根据v,计算q。通过greedy更新策略
但计算Q需要奖励函数和状态转移矩阵,但在MDP未知的情况下无法计算。

因此采用广义的策略迭代。通过MC来计算Q函数
相关文章:

动态规划解决马尔可夫决策过程
马尔可夫决策过程是强化学习中的基本问题模型之一,而解决马尔可夫决策过程的方法我们统称为强化学习算法。 动态规划( dynamic programming, DP )具体指的是在某些复杂问题中,将问题转化为若干个子问题,并在求解每个子…...

ubuntu1604安装及问题解决
虚拟机安装vmbox7 虚拟机操作: 安装增强功能 sudo mkdir /mnt/share sudo mount -t vboxsf sharefolder /mnt/share第一次使用sudo提示is not in the sudoers file. This incident will be reported 你的root需要设置好密码 sudo passwd root 输入如下指令&#x…...
Leetcode—24. 两两交换链表中的节点【中等】
2023每日刷题(八十七) Leetcode—24. 两两交换链表中的节点 实现代码 /*** Definition for singly-linked list.* struct ListNode {* int val;* ListNode *next;* ListNode() : val(0), next(nullptr) {}* ListNode(int x) : val(x),…...

USRP相关报错解决办法
文章目录 前言一、本地环境二、相关报错信息二、解决办法1、更换电脑操作系统2、升级最新版固件 前言 在进行 USRP 开发时遇到了一些报错,这里做个记录解决问题的方法。 一、本地环境 电脑操作系统:Windows11MATLAB 版本:MATLAB 2021aUSRP …...
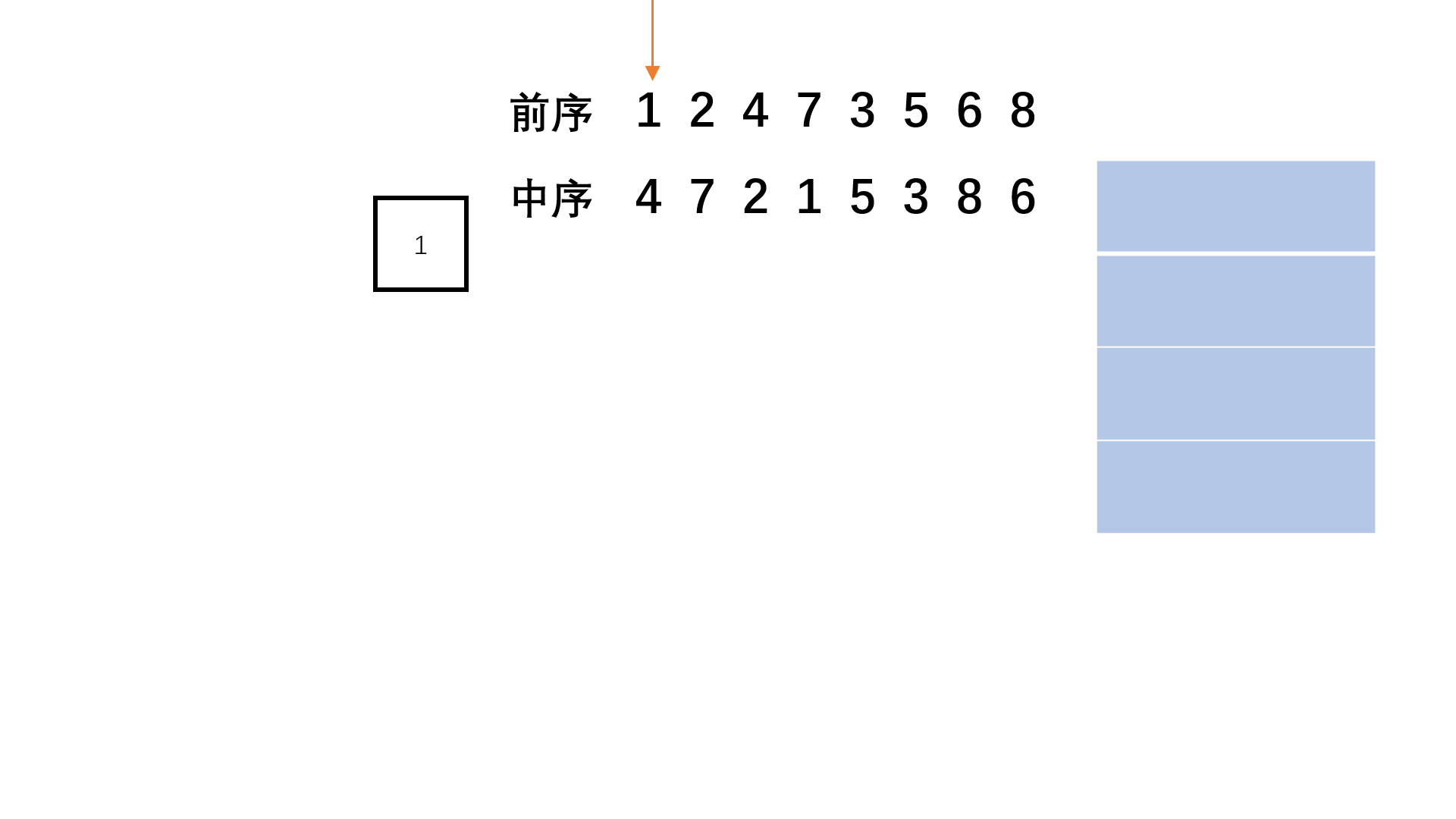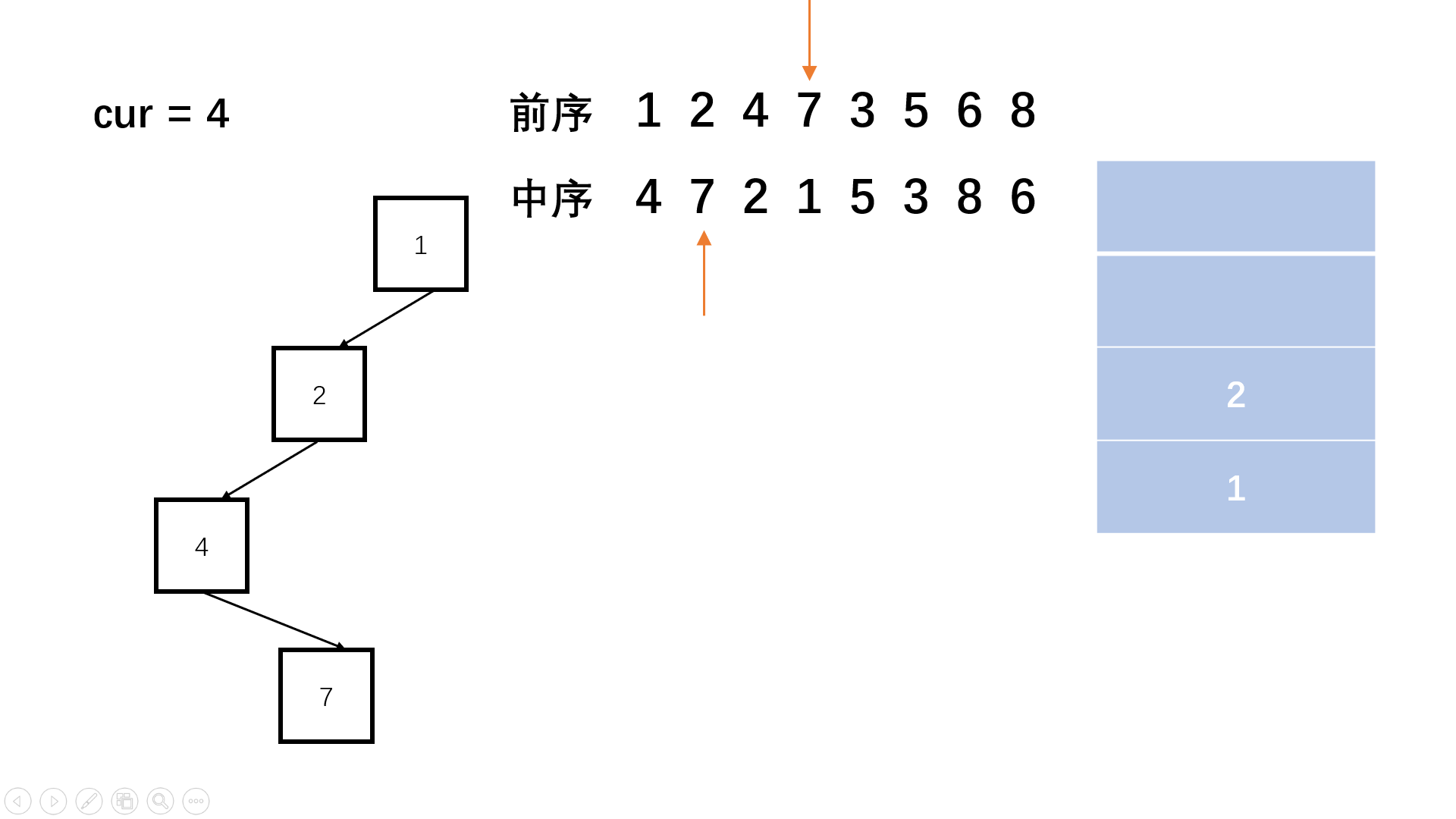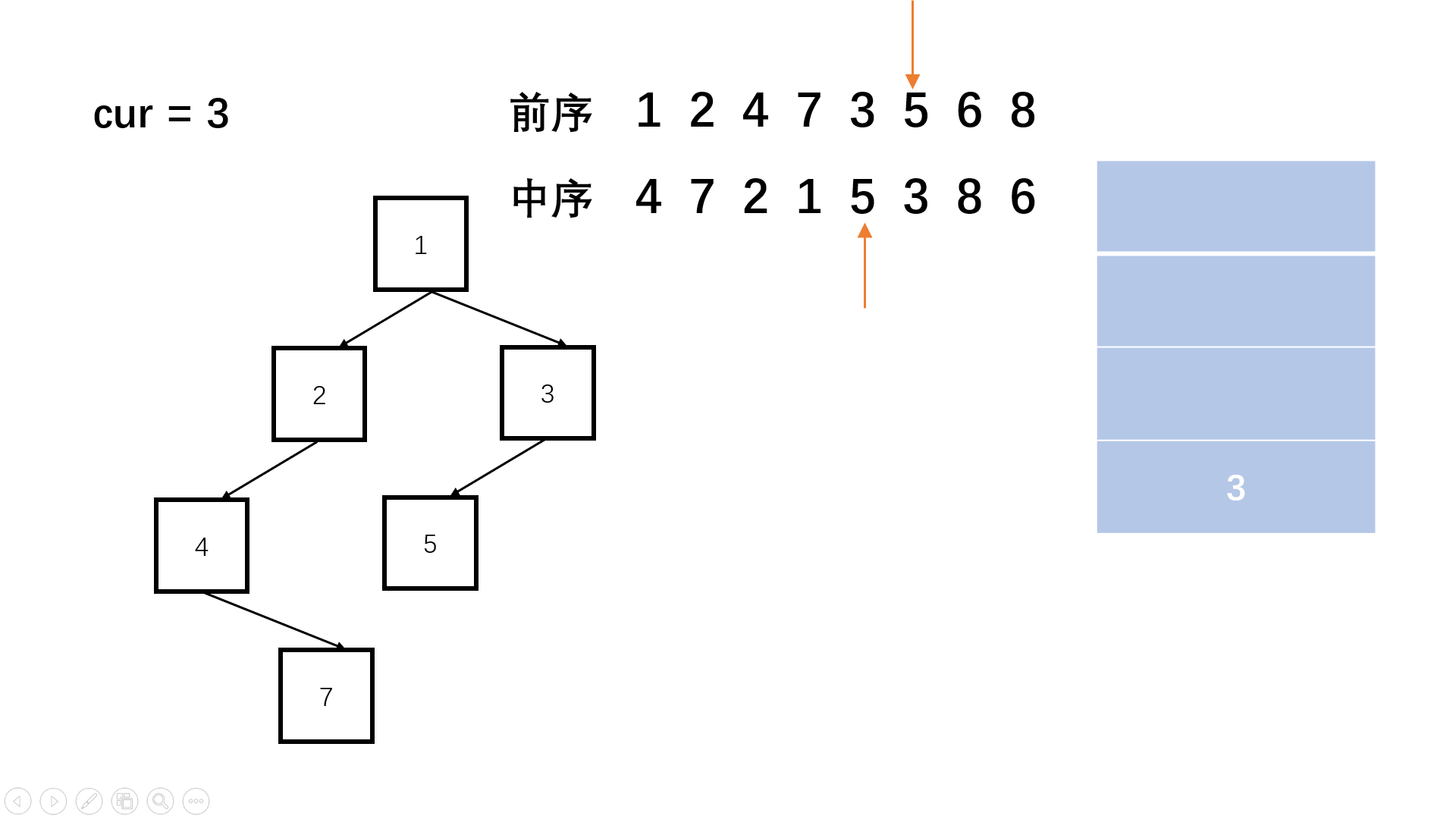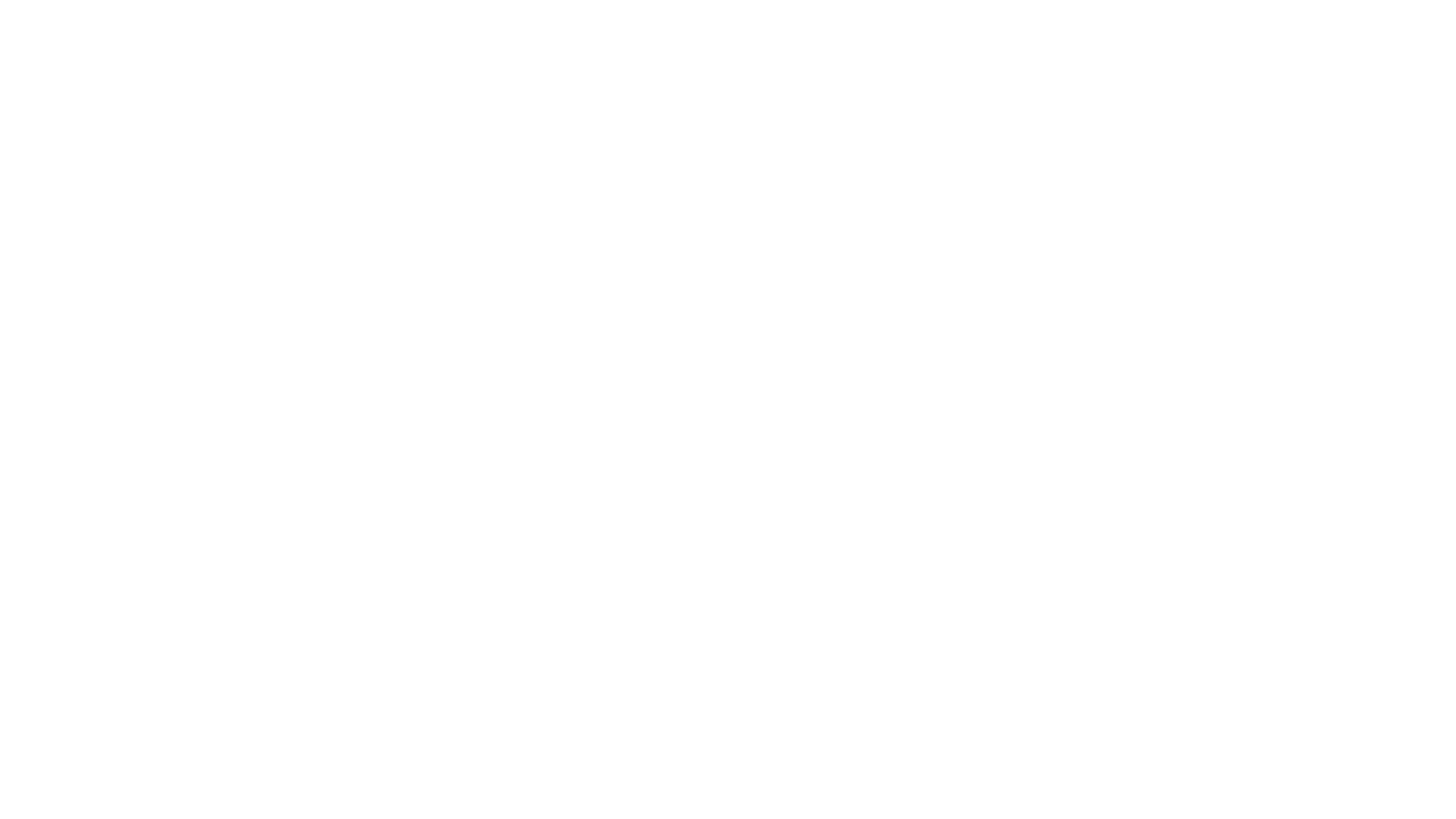
【剑指offer】重建二叉树
👑专栏内容:力扣刷题⛪个人主页:子夜的星的主页💕座右铭:前路未远,步履不停 目录 一、题目描述1、题目2、示例 二、题目分析1、递归2、栈 一、题目描述 1、题目 剑指offer:重建二叉树 给定节…...

中仕教育:事业编招考全流程介绍
一、报名阶段 1. 了解查看招聘信息:查看各类事业编岗位的招聘信息,包括岗位职责、招聘条件、报名时间等。 2. 填写报名表:按照要求填写报名表,包括个人信息、教育背景、工作经历等内容。 3. 提交报名材料:将报名表及…...

149. 直线上最多的点数
149. 直线上最多的点数 class MaxPoints:"""149. 直线上最多的点数https://leetcode.cn/problems/max-points-on-a-line/description/?envTypestudy-plan-v2&envIdtop-interview-150"""def solution(self, points: List[List[int]]) ->…...
不合格机器人工程讲师再读《悉达多》-2024-
一次又一次失败的经历,让我对经典书籍的认同感越来越多,越来越觉得原来的自己是多么多么的无知和愚昧。 ----zhangrelay 唯物也好,唯心也罢,我们都要先热爱这个世界,然后才能在其中找到自己所热爱的事业。 ----zh…...
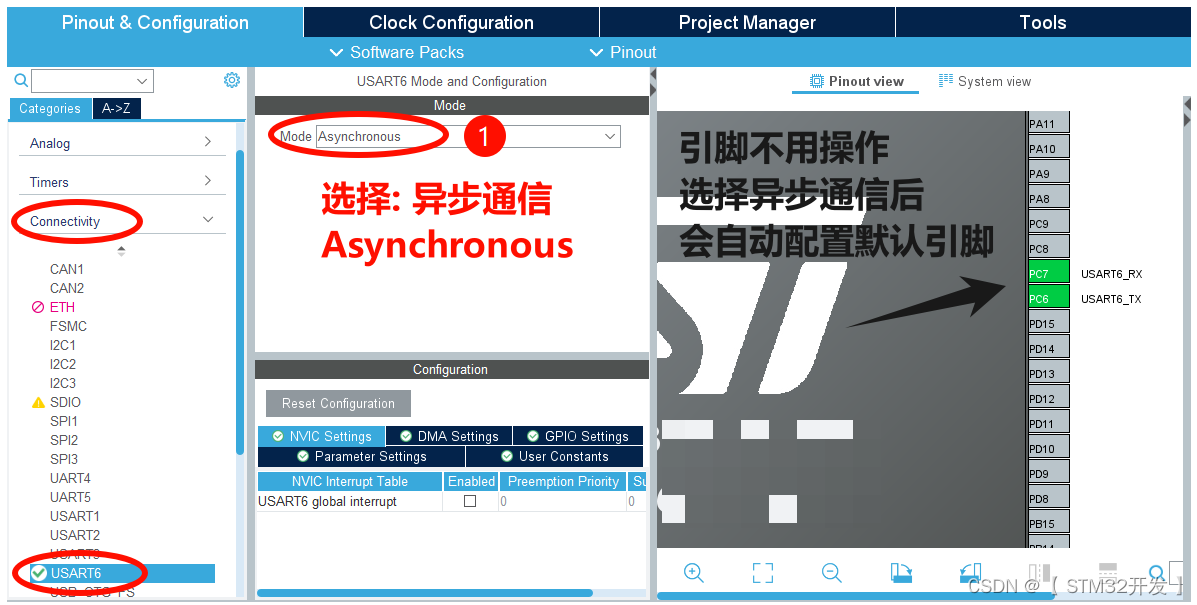
【STM32CubeMX串口通信详解】USART2 -- DMA发送 + DMA空闲中断 接收不定长数据
( 本篇正在编写、更新状态中.....) 文章目录: 前言 前言 本篇,详细地用截图解释 CubeMX 对 USART2 的配置,HAL函数使用,和收发程序的编写。 收、发机制:DMA发送 DAM空闲中断接收。 DMA空…...

Webpack5入门到原理19:React 脚手架搭建
开发模式配置 // webpack.dev.js const path require("path"); const ESLintWebpackPlugin require("eslint-webpack-plugin"); const HtmlWebpackPlugin require("html-webpack-plugin"); const ReactRefreshWebpackPlugin require("…...
苹果眼镜(Vision Pro)的开发者指南(6)-实战应用场景开发 - 游戏、协作、空间音频、WebXR
第一部分:【构建游戏和媒体体验】 了解如何使用visionOS在游戏和媒体体验中创建真正身临其境的时刻。游戏和媒体可以利用全方位的沉浸感来讲述令人难以置信的故事,并以一种新的方式与人们联系。将向你展示可供你入门的visionOS游戏和叙事开发途径。了解如何使用RealityKit有…...
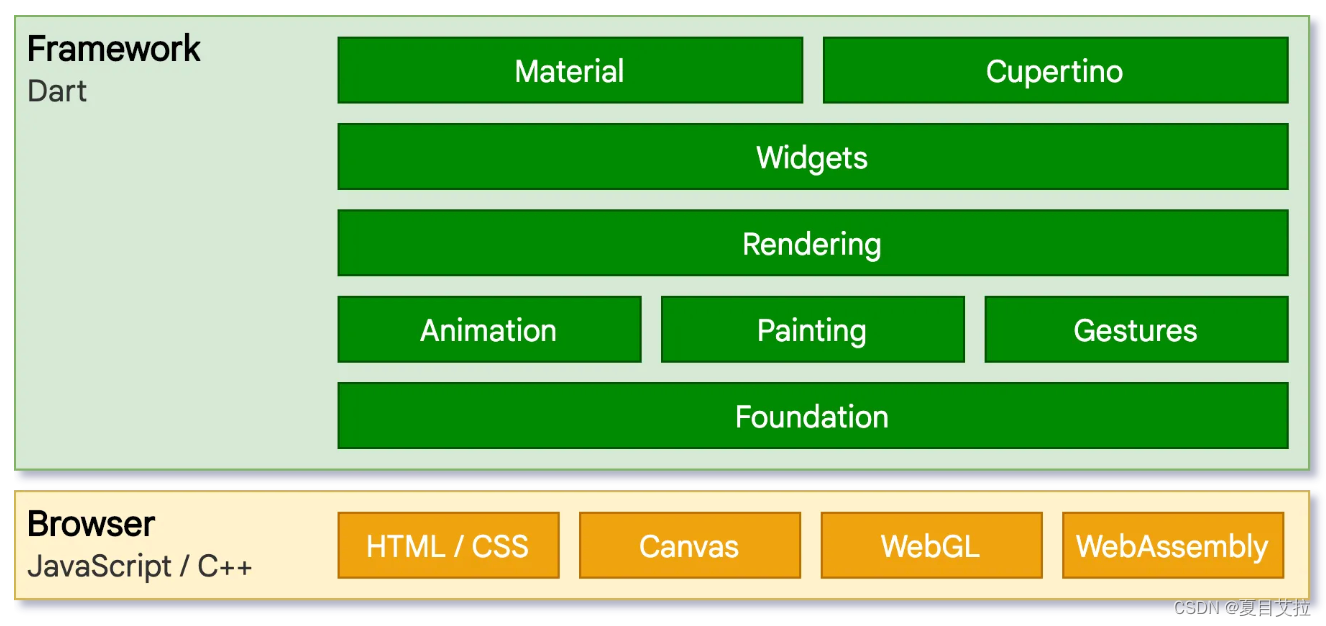
flutter底层架构初探
本文出处:Flutter 中文开发者网站 架构 embedder嵌入层 提供程序入口(其他原生应用也采用此方式),程序由此和底层操作系统协调(surface渲染、辅助功能和输入服务,管理事件循环…...
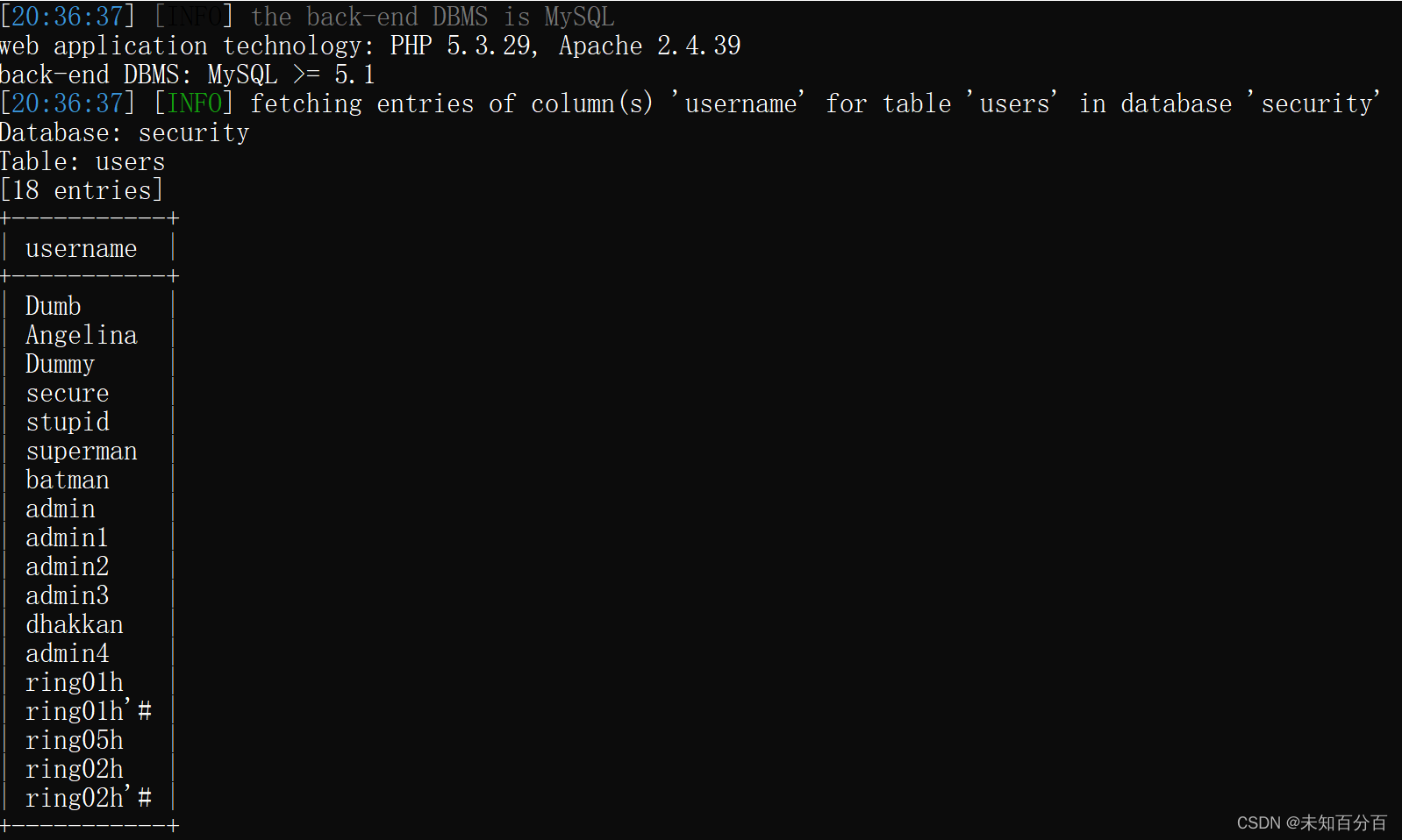
初识SQL注入
目录 注入攻击 SQL注入 手工注入 Information_schema数据库 自动注入 介绍一下这款工具:sqlmap 半自动注入 前面给大家通过学习练习的方式将XSS攻击的几种形式和一些简单的靶场和例题的演示,从本篇开始我将和小伙伴们通过边复习、边练习的方式来进…...
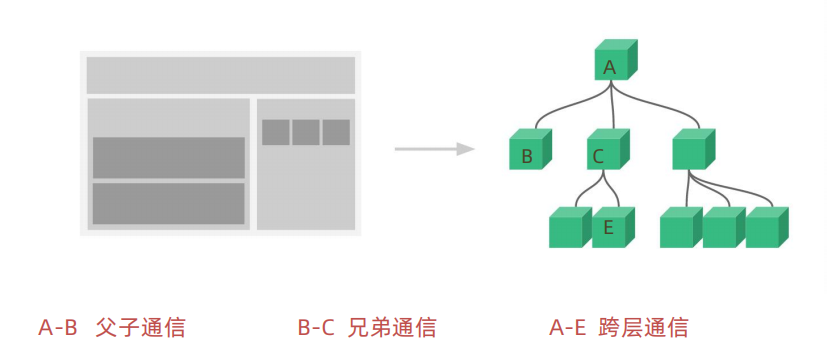
React初探:从环境搭建到Hooks应用全解析
React初探:从环境搭建到Hooks应用全解析 一、React介绍 1、React是什么 React是由Facebook开发的一款用于构建用户界面的JavaScript库。它主要用于构建单页面应用中的UI组件,通过组件化的方式让开发者能够更轻松地构建可维护且高效的用户界面。 Reac…...
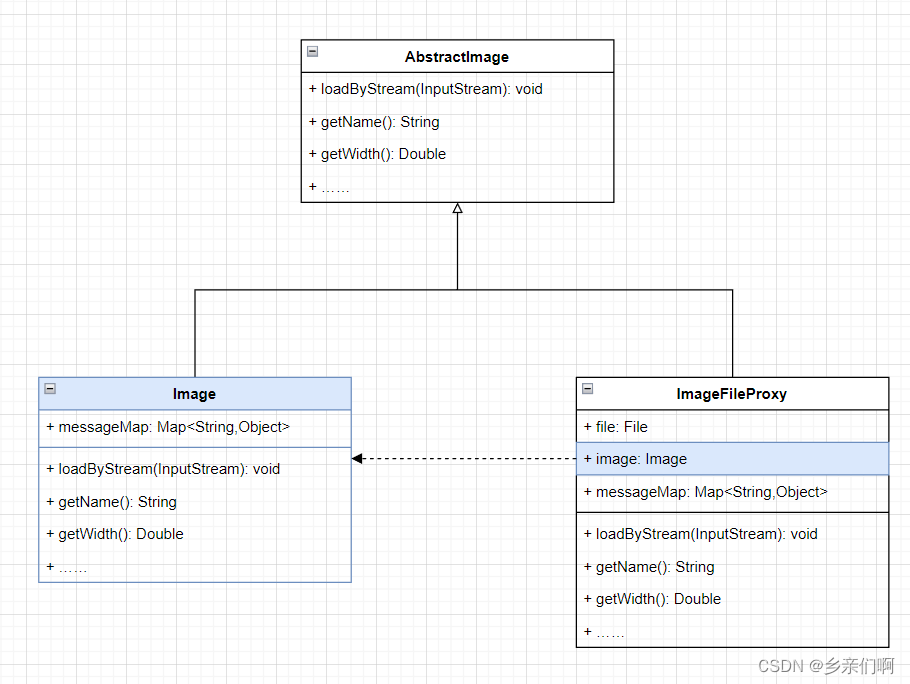
设计模式——1_6 代理(Proxy)
诗有可解不可解,若镜花水月勿泥其迹可也 —— 谢榛 文章目录 定义图纸一个例子:图片搜索器图片加载搜索器直接在Image添加组合他们 各种各样的代理远程代理:镜中月,水中花保护代理:对象也该有隐私引用代理:…...
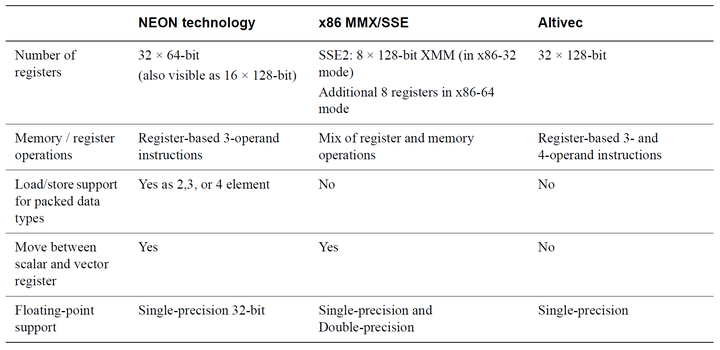
性能优化(CPU优化技术)-NEON 介绍
「发表于知乎专栏《移动端算法优化》」 本节主要介绍基本 SIMD 及其他的指令流与数据流的处理方式,NEON 的基本原理、指令以及与其他平台及硬件的对比。 🎬个人简介:一个全栈工程师的升级之路! 📋个人专栏:…...
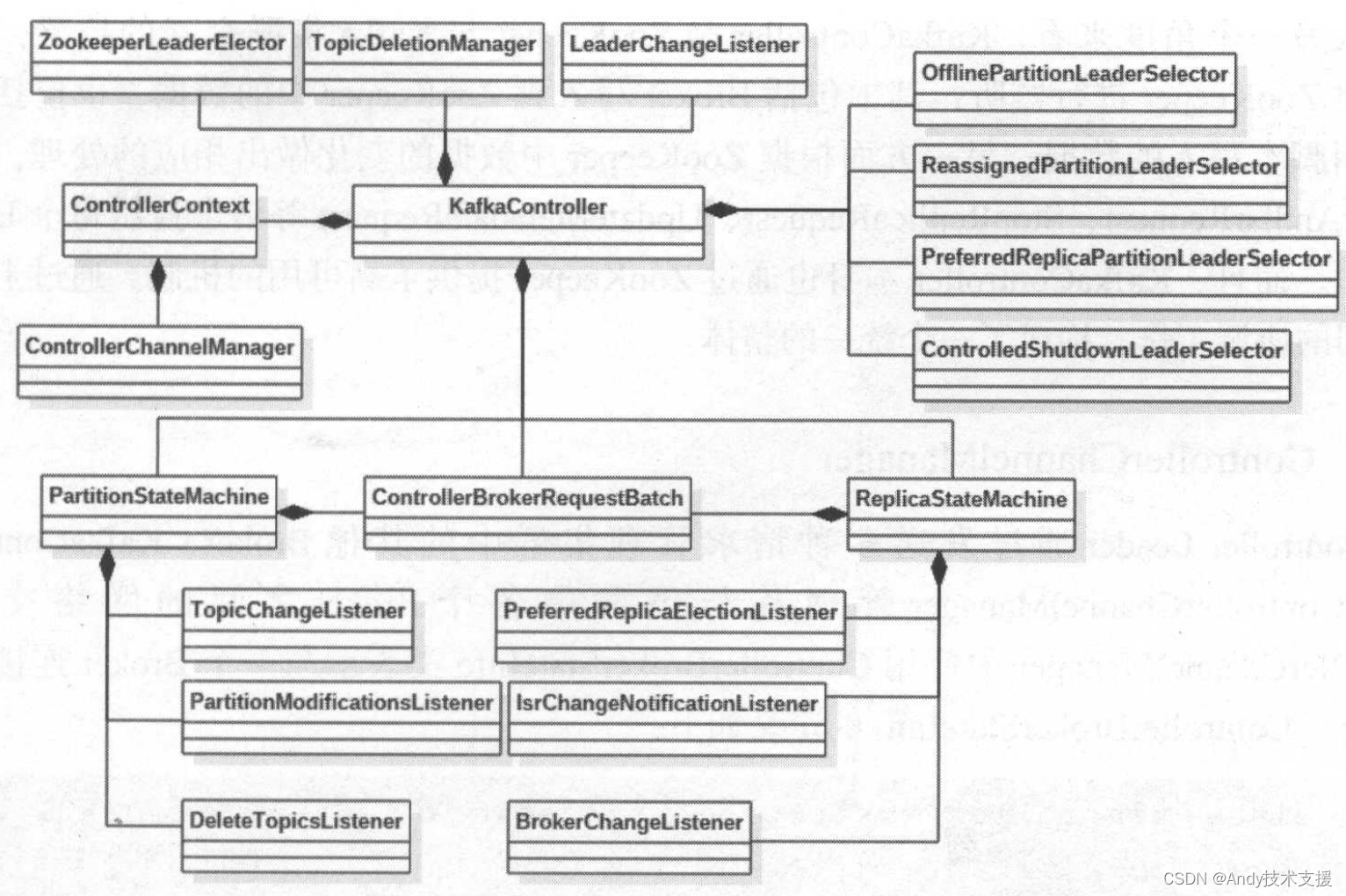
Kafka-服务端-KafkaController
Broker能够处理来自KafkaController的LeaderAndIsrRequest、StopReplicaRequest、UpdateMetadataRequest等请求。 在Kafka集群的多个Broker中,有一个Broker会被选举为Controller Leader,负责管理整个集群中所有的分区和副本的状态。 例如:当某分区的Le…...

ffmpeg使用手册
ffmpeg使用手册 文章目录 ffmpeg使用手册ffmpeg是什么指令总结1.查看ffmpeg版本2.mkv转mp43.裁剪 .mkv 视频4.不调节帧率,尽可能保证原视频质量的情况下将原始视频压缩4.1 crf4.2 preset 5.调节视频帧率6.调节帧率,尽可能保证原视频质量的情况下将原始视…...

操作系统导论-课后作业-ch15
对应异步社区资源HW-Relocation: 1. 种子1运行结果: 种子2运行结果: 种子3运行结果: 2. 需要将界限设置为930,结果如下: 3. 有人说原书翻译有误,原文如下所示: 原文翻译如…...

宝塔面板SRS音视频TRC服务器启动失败
首先,查找原因 1.先看srs服务在哪 find / -type f -name srs 2>/dev/null运行结果: /var/lib/docker/overlay2/5347867cc0ffed43f1ae24eba609637bfa3cc7cf5f8c660976d2286fa6a88d2b/diff/usr/local/srs/objs/srs /var/lib/docker/overlay2/5347867…...

KubeSphere 容器平台高可用:环境搭建与可视化操作指南
Linux_k8s篇 欢迎来到Linux的世界,看笔记好好学多敲多打,每个人都是大神! 题目:KubeSphere 容器平台高可用:环境搭建与可视化操作指南 版本号: 1.0,0 作者: 老王要学习 日期: 2025.06.05 适用环境: Ubuntu22 文档说…...

Linux简单的操作
ls ls 查看当前目录 ll 查看详细内容 ls -a 查看所有的内容 ls --help 查看方法文档 pwd pwd 查看当前路径 cd cd 转路径 cd .. 转上一级路径 cd 名 转换路径 …...

Cloudflare 从 Nginx 到 Pingora:性能、效率与安全的全面升级
在互联网的快速发展中,高性能、高效率和高安全性的网络服务成为了各大互联网基础设施提供商的核心追求。Cloudflare 作为全球领先的互联网安全和基础设施公司,近期做出了一个重大技术决策:弃用长期使用的 Nginx,转而采用其内部开发…...

基于Docker Compose部署Java微服务项目
一. 创建根项目 根项目(父项目)主要用于依赖管理 一些需要注意的点: 打包方式需要为 pom<modules>里需要注册子模块不要引入maven的打包插件,否则打包时会出问题 <?xml version"1.0" encoding"UTF-8…...

android13 app的触摸问题定位分析流程
一、知识点 一般来说,触摸问题都是app层面出问题,我们可以在ViewRootImpl.java添加log的方式定位;如果是touchableRegion的计算问题,就会相对比较麻烦了,需要通过adb shell dumpsys input > input.log指令,且通过打印堆栈的方式,逐步定位问题,并找到修改方案。 问题…...

基于PHP的连锁酒店管理系统
有需要请加文章底部Q哦 可远程调试 基于PHP的连锁酒店管理系统 一 介绍 连锁酒店管理系统基于原生PHP开发,数据库mysql,前端bootstrap。系统角色分为用户和管理员。 技术栈 phpmysqlbootstrapphpstudyvscode 二 功能 用户 1 注册/登录/注销 2 个人中…...

深度解析云存储:概念、架构与应用实践
在数据爆炸式增长的时代,传统本地存储因容量限制、管理复杂等问题,已难以满足企业和个人的需求。云存储凭借灵活扩展、便捷访问等特性,成为数据存储领域的主流解决方案。从个人照片备份到企业核心数据管理,云存储正重塑数据存储与…...

深入理解JavaScript设计模式之闭包与高阶函数
目录 前言小序一场失败面试面试后的觉醒 闭包变量作用域:谁的地盘听谁的变量的生命周期:该走了,不该走的还在闭包的更多作用:不只是谈恋爱,还能干活!1、封装私有变量:你的变量我来守护2、延长变…...

二叉树-226.翻转链表-力扣(LeetCode)
一、题目解析 翻转可以理解为树的左右子树交换,从根到叶子节点,但是这里交换的是链接的指针,而不是单纯的交换值,当出现nullptr时,也是可以交换链接的,交换值的话就不行了。 二、算法原理 依旧的递归&…...

408第一季 - 数据结构 - 栈与队列
栈 闲聊 栈是一个线性表 栈的特点是后进先出 然后是一个公式 比如123要入栈,一共有5种排列组合的出栈 栈的数组实现 这里有两种情况,,一个是有下标为-1的,一个没有 代码不用看,真题不会考 栈的链式存储结构 L ->…...
