# [NOI2019] 斗主地 洛谷黑题题解
[NOI2019] 斗主地
题目背景
时限 4 秒 内存 512MB
题目描述
小 S 在和小 F 玩一个叫“斗地主”的游戏。
可怜的小 S 发现自己打牌并打不过小 F,所以他想要在洗牌环节动动手脚。
一副牌一共有 n n n 张牌,从上到下依次标号为 1 ∼ n 1 \sim n 1∼n。标号为 i i i 的牌分数是 f ( i ) f(i) f(i)。在本题, f ( i ) f(i) f(i) 有且仅有两种可能: f ( i ) = i f(i) = i f(i)=i 或 f ( i ) = i 2 f(i) = i^2 f(i)=i2。
洗牌的方式和我们日常生活中的比较类似,以下我们用形式化的语言来定义: 洗牌环节一共分 m m m 轮,这 m m m 轮洗牌依次进行。第 i i i 轮洗牌时:
- 小 S 会拿出从最上面往下数的前 A i A_i Ai 张牌。这样这副牌就被分成了两堆:第一堆 是最上面的 A i A_i Ai 张牌,第二堆是剩下的 n − A i n-A_i n−Ai 张牌,且这两堆牌内相对顺序不变。 特别地,当 A i = n A_i = n Ai=n 或 A i = 0 A_i = 0 Ai=0 时,有一堆牌是空的。
- 接下来对两堆牌进行合并,从而产生新的第三堆牌。当第一堆牌还剩下 X X X 张,第二堆牌还剩下 Y Y Y 张的时候,以 X X + Y \dfrac{X}{X+Y} X+YX 的概率取出第一堆牌的最下面的牌,并将它 放入新的第三堆牌的最上面, Y X + Y \dfrac{Y}{X+Y} X+YY 的概率取出第二堆牌的最下面的牌,并将它放入新的第三堆牌的最上面
- 重复操作 2 2 2,一直取到两堆牌都为空为止。这样我们就完成了一轮洗牌。
因为洗牌过程是随机的,所以小 S 发现自己没法知道某个位置上具体是哪张牌。但小 S 想问你在经历了这 m m m 轮洗牌后,某个位置上的牌的期望分数是多少。小 S 一共会问你 Q Q Q 个这样的问题。
输入格式
输入的第一行包含三个正整数 n , m , t y p e n, m, type n,m,type,分别表示牌的数量,洗牌的轮数与 f ( i ) f(i) f(i) 的类型。当 t y p e = 1 type = 1 type=1 时, f ( i ) = i f(i) = i f(i)=i。当 t y p e = 2 type = 2 type=2 时, f ( i ) = i 2 f(i) = i^2 f(i)=i2。
接下来一行,一共 m m m 个整数,表示 A 1 ∼ A m A_1 \sim A_m A1∼Am。
接下来一行一个正整数 Q Q Q,表示小 S 的询问个数。 接下来 Q Q Q 行,每行一个正整数 c i c_i ci,表示小 S 想要知道从上往下第 c i c_i ci 个位置上的牌的期望分数。
保证 1 ≤ c i ≤ n 1 \leq c_i \leq n 1≤ci≤n。
输出格式
输出一共 Q Q Q 行,每行一个整数,表示答案在模 998244353 998244353 998244353 意义下的取值。
即设答案化为最简分式后的形式为 a b \dfrac{a} {b} ba,其中 a a a 和 b b b 互质。输出整数 x x x 使得 b x ≡ a ( m o d 998244353 ) bx \equiv a \pmod{998244353} bx≡a(mod998244353) 且 0 ≤ x < 998244353 0 ≤ x < 998244353 0≤x<998244353。可以证明这样的整数 x x x 是唯一的。
样例 #1
样例输入 #1
4 1 1
3
1
1
样例输出 #1
249561090
提示
更多样例
您可以通过附加文件获得更多样例。
样例 2
见附加文件中的 landlords/landlords2.in 与 landlords/landlords2.ans。
样例 3
见附加文件中的 landlords/landlords3.in 与 landlords/landlords3.ans。
样例输入输出 1 解释
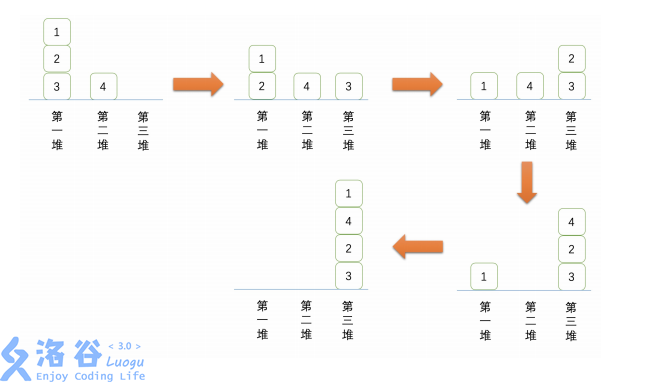
- 有 1 4 \dfrac{1}{4} 41 的概率从上到下的最终结果是 { 1 , 2 , 3 , 4 } \{1, 2, 3, 4\} {1,2,3,4}。
- 有 1 4 \dfrac{1}{4} 41 的概率从上到下的最终结果是 { 1 , 2 , 4 , 3 } \{1, 2, 4, 3\} {1,2,4,3}。
- 有 1 4 \dfrac{1}{4} 41 的概率从上到下的最终结果是 { 1 , 4 , 2 , 3 } \{1, 4, 2, 3\} {1,4,2,3}。
- 有 1 4 \dfrac{1}{4} 41 的概率从上到下的最终结果是 { 4 , 1 , 2 , 3 } \{4, 1, 2, 3\} {4,1,2,3}。
所以最终有 1 4 \dfrac{1}{4} 41 的概率第一个位置是 4 4 4,有 3 4 \dfrac{3} {4} 43 的概率第一个位置是 1 1 1,所以第一个位置的期望分数是 7 4 \dfrac{7}{ 4} 47。
为了帮助你们更直观地了解洗牌的过程,我们在下面画出了结果是 { 1 , 4 , 2 , 3 } \{1, 4, 2, 3\} {1,4,2,3} 的过程。
数据规模与约定
对于全部的测试点,保证 3 ≤ n ≤ 1 0 7 3\le n \le 10^7 3≤n≤107, 1 ≤ m , Q ≤ 5 × 1 0 5 1\le m,Q\le5\times 10^5 1≤m,Q≤5×105, 0 ≤ A i ≤ n 0\le A_i\le n 0≤Ai≤n, t y p e ∈ { 1 , 2 } type\in \{1,2\} type∈{1,2}。
每个测试点的具体限制见下表:
| 测试点 | n n n | m m m | t y p e = type= type= | 其他性质 |
|---|---|---|---|---|
| 1 1 1 | ≤ 10 \le 10 ≤10 | ≤ 1 \le 1 ≤1 | 1 1 1 | 无 |
| 2 2 2 | ≤ 80 \le 80 ≤80 | ≤ 80 \le 80 ≤80 | 1 1 1 | 无 |
| 3 3 3 | ≤ 80 \le 80 ≤80 | ≤ 80 \le 80 ≤80 | 2 2 2 | 无 |
| 4 4 4 | ≤ 100 \le 100 ≤100 | ≤ 5 × 1 0 5 \le 5\times 10^5 ≤5×105 | 2 2 2 | 所有 A i A_i Ai 相同 |
| 5 5 5 | ≤ 1 0 7 \le 10^7 ≤107 | ≤ 5 × 1 0 5 \le 5\times 10^5 ≤5×105 | 1 1 1 | 无 |
| 6 6 6 | ≤ 1 0 7 \le 10^7 ≤107 | ≤ 5 × 1 0 5 \le 5\times 10^5 ≤5×105 | 1 1 1 | 无 |
| 7 7 7 | ≤ 1 0 7 \le 10^7 ≤107 | ≤ 5 × 1 0 5 \le 5\times 10^5 ≤5×105 | 1 1 1 | 无 |
| 8 8 8 | ≤ 1 0 7 \le 10^7 ≤107 | ≤ 5 × 1 0 5 \le 5\times 10^5 ≤5×105 | 2 2 2 | 无 |
| 9 9 9 | ≤ 1 0 7 \le 10^7 ≤107 | ≤ 5 × 1 0 5 \le 5\times 10^5 ≤5×105 | 2 2 2 | 无 |
| 10 10 10 | ≤ 1 0 7 \le 10^7 ≤107 | ≤ 5 × 1 0 5 \le 5\times 10^5 ≤5×105 | 2 2 2 | 无 |
请注意我们并没有保证 Q ≤ n Q\le n Q≤n。
提示
这里我们给出离散型随机变量 X X X 的期望 E [ x ] \mathbb{E}[x] E[x] 的定义:
设离散随机变量 X X X 的可能值是 X 1 , X 2 , … X k X_1,X_2,\ldots X_k X1,X2,…Xk, P r [ X 1 ] , P r [ X 2 ] , … , P r [ X k ] Pr[X_1],Pr[X_2],\ldots,Pr[X_k] Pr[X1],Pr[X2],…,Pr[Xk] 为 X X X 取对应值的概率,则 X X X 的期望为:
E [ x ] = ∑ i = 1 k X i × P r [ X i ] \mathbb{E}[x]=\sum^k_{i=1}X_i\times Pr[X_i] E[x]=i=1∑kXi×Pr[Xi]
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int kcz=998244353;
const int maxn=10000005;
ll a,b,c,f[maxn];
int n;
inline ll qpow(ll a,ll k)
{ll res=1;while(k){if(k&1) res=res*a%kcz;if(k>>=1) a=a*a%kcz;}return res;
}
inline ll calc(ll x) { return ((a*x+b)%kcz*x+c)%kcz; } // 算第x个数的期望
int main()
{int m,tp,i;ll _,__,t1,t2,t3,t,___,sqn;freopen("landlords.in","r",stdin),freopen("landlords.out","w",stdout);scanf("%d%d%d",&n,&m,&tp),sqn=n*(ll)n%kcz;_=qpow(n-1,kcz-2),__=qpow(n,kcz-2),___=qpow((-sqn+3*n-2)%kcz,kcz-2);if(tp==1) a=c=0,b=1;else a=1,b=c=0; // x_i=ai^2+bi+cwhile(m--){scanf("%lld",&t);if(t==0 || t==n) continue;t1=(calc(1)*t+calc(t+1)*(n-t))%kcz*__%kcz; // 第一个t2=((calc(2)*(t-1)+calc(t+1)*(n-t))%kcz*t+(calc(1)*t+calc(t+2)*(n-t-1))%kcz*(n-t))%kcz*__%kcz*_%kcz; // 第二个t3=(calc(t)*t+calc(n)*(n-t))%kcz*__%kcz; // 第n个a=((2-n)*t1+(n-1)*t2-t3)%kcz*___%kcz;b=((sqn-4)*t1+(1-sqn)*t2+3*t3)%kcz*___%kcz;c=((4*n-2*sqn)*t1+(sqn-n)*t2-2*t3)%kcz*___%kcz; // 极其丑的差值}for(i=1;i<=n;i++)f[i]=(calc(i)+kcz)%kcz;scanf("%d",&m);while(m--)scanf("%lld",&t),printf("%lld\n",f[t]);fclose(stdin),fclose(stdout);return 0;
}
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int kcz=998244353;
const int maxn=10000005;
ll a,b,c,a_,b_,c_,fac[maxn],inv[maxn],inv_fac[maxn];
int n;
inline ll f(ll x) { return (a+b*(x-1)+c*(x-1)%kcz*(x-2))%kcz; } // 算第x个数的期望
inline ll C(int n,int m) { return (m>=0 && m<=n)?fac[n]*inv_fac[m]%kcz*inv_fac[n-m]%kcz:0; } // 判一下0的情况
inline ll invC(int n,int m) { return inv_fac[n]*fac[m]%kcz*fac[n-m]%kcz; }
int main()
{int i,q,op,A;ll t;freopen("landlords.in","r",stdin),freopen("landlords.out","w",stdout);scanf("%d%d%d",&n,&q,&op);if(op==1) a=b=1,c=0; // a_i=a+b*(i-1)+c*(i-1)*(i-2)else a=1,b=3,c=1;fac[0]=inv_fac[0]=inv[1]=fac[1]=inv_fac[1]=1;for(i=2;i<=n;i++){fac[i]=fac[i-1]*i%kcz;inv[i]=-(kcz/i)*inv[kcz%i]%kcz;inv_fac[i]=inv_fac[i-1]*inv[i]%kcz;}while(q--){scanf("%d",&A);a_=(a+b*A+c*A%kcz*(A-1ll))%kcz; // 平移x->x+Ab_=(b+c*2*A)%kcz;c_=c;t=invC(n,A);a=(a*C(n-1,A-1)+a_*C(n-1,n-A-1))%kcz*t%kcz; // 更新系数b=(b*C(n-2,A-2)+b_*C(n-2,n-A-2))%kcz*t%kcz;c=(c*C(n-3,A-3)+c_*C(n-3,n-A-3))%kcz*t%kcz;}scanf("%d",&q);while(q--)scanf("%d",&i),printf("%lld\n",(f(i)+kcz)%kcz);fclose(stdin),fclose(stdout);return 0;
}
#include <bits/stdc++.h>
#define ll long long
using namespace std;
const int maxn=500000+10;
const int maxm=10000000+10;
const int mod=998244353;
const int inv2=(mod+1)>>1;
int n,m,q,type;ll A,B,C,f[10][10],g[10],h[10],w[10],inv[maxm];inline ll F(int x) {return (A*x%mod*x+B*x+C)%mod;}int main()
{scanf("%d%d%d",&n,&m,&type);inv[0]=inv[1]=1;for(int i=2;i<=n;i++) inv[i]=(mod-mod/i)*inv[mod%i]%mod;if(type==1) A=0,B=1,C=0;else A=1,B=0,C=0;int tmp;ll X,Y,Z;for(int i=1;i<=m;i++){scanf("%d",&tmp);for(int j=1;j<=3;j++) g[j]=F(j),h[j]=F(j+tmp),w[j]=0;for(int j=0;j<3;j++)for(int k=0;k<3;k++) f[j][k]=0;f[0][0]=1;for(int j=0;j<3;j++)for(int k=0;k<3;k++){if(j+k>=3) break;if(j<tmp){ll val=f[j][k]*(tmp-j)%mod*inv[n-j-k]%mod;(f[j+1][k]+=val)%=mod;(w[j+k+1]+=val*g[j+1])%=mod;}if(k<n-tmp){ll val=f[j][k]*(n-tmp-k)%mod*inv[n-j-k]%mod;(f[j][k+1]+=val)%=mod;(w[j+k+1]+=val*h[k+1])%=mod;}}X=w[1];Y=w[2];Z=w[3];A=((Z-2*Y+X)*inv2%mod+mod)%mod;B=((8*Y-5*X-3*Z)*inv2%mod+mod)%mod;C=((3*X-3*Y+Z)%mod+mod)%mod;}scanf("%d",&q);while(q--){scanf("%d",&tmp);printf("%lld\n",F(tmp));}return 0;
}
相关文章:

# [NOI2019] 斗主地 洛谷黑题题解
[NOI2019] 斗主地 题目背景 时限 4 秒 内存 512MB 题目描述 小 S 在和小 F 玩一个叫“斗地主”的游戏。 可怜的小 S 发现自己打牌并打不过小 F,所以他想要在洗牌环节动动手脚。 一副牌一共有 n n n 张牌,从上到下依次标号为 1 ∼ n 1 \sim n 1∼…...
Redisson调用unlockAsync方法释放锁失败)
踩坑(6)Redisson调用unlockAsync方法释放锁失败
问题描述 通过redisson的lockAsync异步方法获取到锁之后,再业务执行完成后调用lock.unlockAsync()无法释放当前锁,导致后续的方法被阻塞 public void asyncLock() {RLock lock redissonClient.getLock("asyncLock");RFuture<Void> fut…...

树莓派实战应用:基于人脸识别系统
引言: 随着人工智能技术的不断发展,人脸识别技术已经广泛应用于各种场景,如门禁系统、安全监控等。树莓派作为一种功能强大的迷你计算机,也可以用于搭建人脸识别检测系统。 一、项目简介 人脸识别系统是一种基于人工智能技术的身…...

5G赋能智慧文旅:科技与文化的完美结合,打造无缝旅游体验,重塑旅游业的未来
一、5G技术:智慧文旅的强大引擎 5G技术的起源可以追溯到2010年,当时世界各国开始意识到4G技术已经达到了瓶颈,无法满足日益增长的移动通信需求。2013年,国际电信联盟(ITU)成立了5G技术研究组,开…...

大模型:相关参数总结
文章目录 一、相关参数 一、相关参数 参数名称是否必填默认值描述model是调用的模型名称message是传入模型的消息max_tokens否返回tokens的数量temperature否top_p否n否表示一个问答返回几个回答的结果信息stream否false表示应答的方式,false表示返回全部的结果&am…...

腾讯云短信开发
短信服务应用申请 """ 准备工作 1)创建短信应用 - 应用管理 2)申请短信签名 - 国内短信 > 签名管理 3)申请短信模块 - 国内短信 > 正文模板管理 """python中开发腾讯云短信服务 """ 1…...

Dockerfile:如何写一个Dockerfile文件?
如何写一个Dockerfile文件? 🚨推荐参考:Dockerfile:如何写一个Dockerfile文件? 现在的项目肯定都离不开docker,只要是流水线部署就会涉及Dockerfile文件,那么如何写一个正确的编写一个Dockerfil…...

Lua 中的高级特性:模块的使用、字符串模式匹配、高阶函数和表的元方法
### 1. 模块的使用 在 Lua 中,模块是一种封装代码的方式,使得代码可以被重用。下面是一个简单的模块定义和使用的示例: lua -- 定义一个名为 mymodule 的模块 mymodule {} function mymodule.sayHello() print("Hello from my mo…...

openssl3.2/test/certs - 040 - EC cert with named curve signed by named curve ca
文章目录 openssl3.2/test/certs - 040 - EC cert with named curve signed by named curve ca概述笔记END openssl3.2/test/certs - 040 - EC cert with named curve signed by named curve ca 概述 openssl3.2 - 官方demo学习 - test - certs 笔记 /*! * \file D:\my_dev…...
LabVIEW准分子激光器控制系统
LabVIEW准分子激光器控制系统是为了实现准分子激光光源在工业、医疗和科研领域的应用集成及其功能的扩展。系统由PC端和激光器端两部分构成,通过光隔离的RS232通讯连接,以实现稳定可靠的控制与通信。 系统主要由微控制单元(MCU)主…...

热血江湖服务端服务器架设教程
热血江湖服务端服务器架设教程 大家好,我是艾西今天简单的说下热血江湖架设需要哪些东西然后怎么操作,不管你是自己玩还是对外开放,这对于有兴趣的小伙伴总的都是一件好事。技多不压身就是这么个道理,当你需要用上时还希望能记起…...

美易平台:美元指数微幅回落
在最新的金融市场动态中,美元指数经历了0.5%的下跌,报告显示当前指数为103.03。这一变化对全球经济和货币市场产生了一定的影响。在这样的市场环境下,互联网金融券商如美易makeasy平台如何应对变化,并保持其服务质量和客户资产安全…...
编译和链接---C语言
引言 众所周知,C语言是一门高级的编程语言,是无法被计算机直接读懂的,C语言也不同于汇编PHP,无法直接翻译成机器语言,在学习的过程中,你是否好奇过我们所敲的C语言代码,是如何一步步翻译成机器…...

SAP EXCEL上传行数限制问题(ALSM_EXCEL_TO_INTERNAL_TABLE)
标准函数ALSM_EXCEL_TO_INTERNAL_TABLE上传EXCEL函数限制上限是9999行,如果上传数据记录数超过9999行的情况,需要拷贝标准的函数封装一个自定义的函数进行处理 标准的函数ROW的长度为4位,如下图所示 因此,如果想行数的位数超过4位…...

3.召回率-机器学习模型性能的常用的评估指标
在机器学习领域,召回率是一个关键的性能指标,用于评估模型在正样本中正确识别的能力。召回率的计算涉及到模型成功检测到的正样本数量与实际正样本的总数量之比。这个指标对于很多应用场景都至关重要,尤其是在那些要求较高的领域,…...
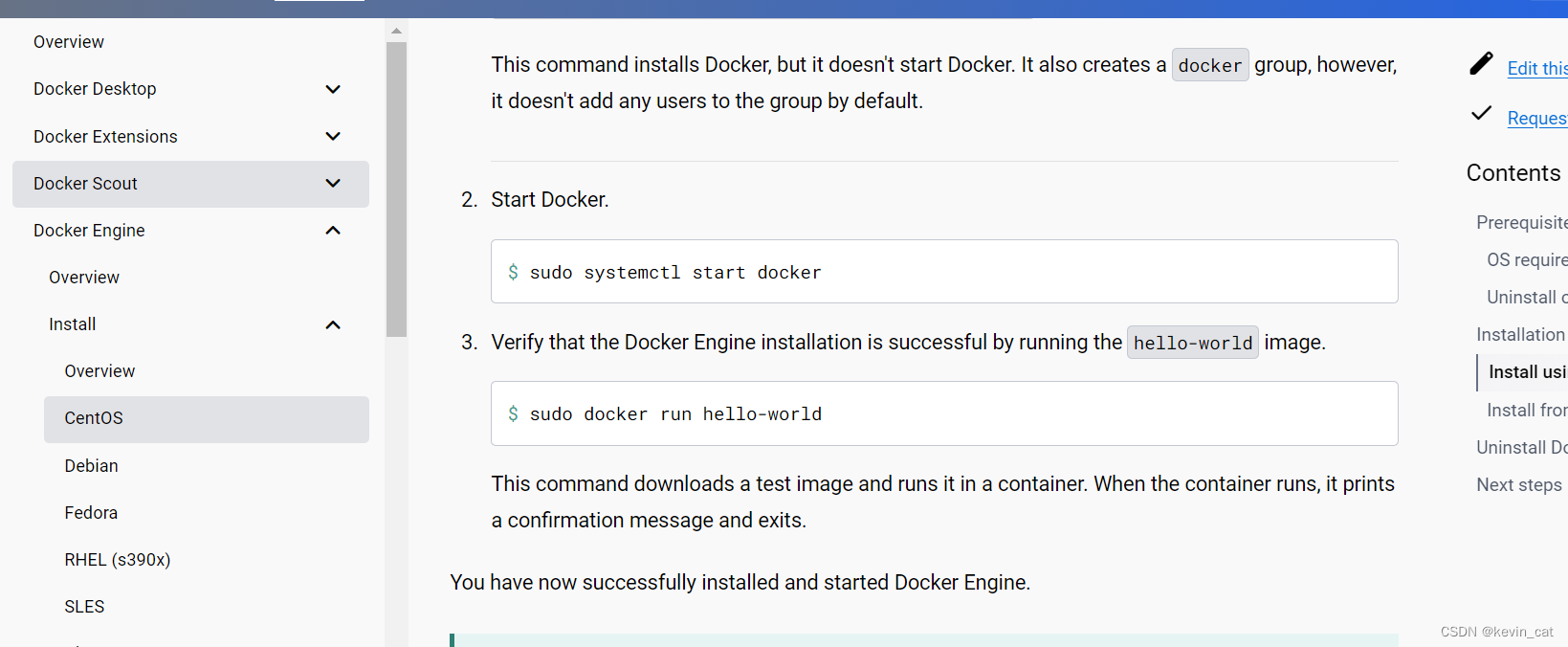
linux安装docker--更具官网教程
1.访问https://docs.docker.com/ 2.进入download 3输入cento 或者直接访问地址Install Docker Engine on CentOS | Docker Docs 4一步一步根据官网命令走 2安装 3 4 方式一: service docker start(开启) service docker status(…...

云原生安全:风险挑战与安全架构设计策略
概述 数字化转型已经成为当今最流行的话题之一,大部分企业已经开启自身的数字化转型之旅,在未来企业只有数字化企业和非数字化企业之分。通过数字经济的加速发展,可以有效推动企业数字化转型的步伐。云计算作为数字化转型的底座和重要的载体…...

c语言-文件的读写操作
文章目录 前言一、文件基础1.1 文件的分类1.2 文件路径和文件名 二、文件的打开和关闭2.1 文件指针2.2 文件的打开和关闭 总结 前言 本篇文章介绍c语言的文件读写操作。 一、文件基础 1.1 文件的分类 在c语言中,从文件的功能角度来看,文件可分为以下两…...

Python处理日期和时间库之arrow使用详解
概要 日期和时间处理是许多应用程序中的常见任务,但在 Python 中,标准库中的 datetime 模块有时可能会让这些任务变得复杂和繁琐。幸运的是,有一个名为 Arrow 的第三方库,它提供了简化日期和时间处理的功能,使其更加直…...
架构师之路(十四)计算机网络(网络层)
前置知识(了解):计算机基础。 作为架构师,我们所设计的系统很少为单机系统,因此有必要了解计算机和计算机之间是怎么联系的。局域网的集群和混合云的网络有啥区别。系统交互的时候网络会存在什么瓶颈。 网络层提供主机…...

【WiFi帧结构】
文章目录 帧结构MAC头部管理帧 帧结构 Wi-Fi的帧分为三部分组成:MAC头部frame bodyFCS,其中MAC是固定格式的,frame body是可变长度。 MAC头部有frame control,duration,address1,address2,addre…...

Swift 协议扩展精进之路:解决 CoreData 托管实体子类的类型不匹配问题(下)
概述 在 Swift 开发语言中,各位秃头小码农们可以充分利用语法本身所带来的便利去劈荆斩棘。我们还可以恣意利用泛型、协议关联类型和协议扩展来进一步简化和优化我们复杂的代码需求。 不过,在涉及到多个子类派生于基类进行多态模拟的场景下,…...

【解密LSTM、GRU如何解决传统RNN梯度消失问题】
解密LSTM与GRU:如何让RNN变得更聪明? 在深度学习的世界里,循环神经网络(RNN)以其卓越的序列数据处理能力广泛应用于自然语言处理、时间序列预测等领域。然而,传统RNN存在的一个严重问题——梯度消失&#…...

ServerTrust 并非唯一
NSURLAuthenticationMethodServerTrust 只是 authenticationMethod 的冰山一角 要理解 NSURLAuthenticationMethodServerTrust, 首先要明白它只是 authenticationMethod 的选项之一, 并非唯一 1 先厘清概念 点说明authenticationMethodURLAuthenticationChallenge.protectionS…...

NLP学习路线图(二十三):长短期记忆网络(LSTM)
在自然语言处理(NLP)领域,我们时刻面临着处理序列数据的核心挑战。无论是理解句子的结构、分析文本的情感,还是实现语言的翻译,都需要模型能够捕捉词语之间依时序产生的复杂依赖关系。传统的神经网络结构在处理这种序列依赖时显得力不从心,而循环神经网络(RNN) 曾被视为…...

mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包
文章目录 现象:mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包遇到 rpm 命令找不到已经安装的 MySQL 包时,可能是因为以下几个原因:1.MySQL 不是通过 RPM 包安装的2.RPM 数据库损坏3.使用了不同的包名或路径4.使用其他包…...

LLMs 系列实操科普(1)
写在前面: 本期内容我们继续 Andrej Karpathy 的《How I use LLMs》讲座内容,原视频时长 ~130 分钟,以实操演示主流的一些 LLMs 的使用,由于涉及到实操,实际上并不适合以文字整理,但还是决定尽量整理一份笔…...

【Linux】Linux 系统默认的目录及作用说明
博主介绍:✌全网粉丝23W,CSDN博客专家、Java领域优质创作者,掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java技术领域✌ 技术范围:SpringBoot、SpringCloud、Vue、SSM、HTML、Nodejs、Python、MySQL、PostgreSQL、大数据、物…...

scikit-learn机器学习
# 同时添加如下代码, 这样每次环境(kernel)启动的时候只要运行下方代码即可: # Also add the following code, # so that every time the environment (kernel) starts, # just run the following code: import sys sys.path.append(/home/aistudio/external-libraries)机…...

从物理机到云原生:全面解析计算虚拟化技术的演进与应用
前言:我的虚拟化技术探索之旅 我最早接触"虚拟机"的概念是从Java开始的——JVM(Java Virtual Machine)让"一次编写,到处运行"成为可能。这个软件层面的虚拟化让我着迷,但直到后来接触VMware和Doc…...
