二叉树
目录
1翻转二叉树
2对称二叉树
3二叉树的深度
最大深度
最小深度
4二叉树的结点数量
完全二叉树的结点数量
5平衡二叉树
6 中序 后序求前序
二叉树结构体如下:
struct freenode {int data;struct freenode *lchild, *rchild;//左孩子 右孩子
}T;1翻转二叉树
给你一个二叉树,让你向如图这样进行翻转

思路
给一个二叉树进行翻转,实际就是交换每个结点的左右孩子指针,遍历使用前序,后序;中序比较麻烦
伪代码如下:
先序遍历
void nb(struct freenode *T)//传入根结点
{if (T == NULL)//如果结点指针为空直接结束return;struct freenode *t;t = T->lchild; T->lchild = T->rchild; T->rchild = t;nb(T->lchild);//左孩子nb(T->rchild);//右孩子return;
}
后序遍历
void nb(struct freenode *T)//传入根结点
{if (T == NULL)//如果结点指针为空直接结束return;nb(T->lchild);//左孩子nb(T->rchild);//右孩子struct freenode *t;//定义t用于交换t = T->lchild; T->lchild = T->rchild; T->rchild = t;return;
}
2对称二叉树
给你一个二叉树,判断二叉树是否对称

思路
判断二叉树是否对称,根据图片可以看出,只需判断根结点的左右子树是否互为翻转,注意只能使用后序遍历,因为只有左右子树结点全部比较完才能确定是否为对称二叉树。
伪代码如下
//1为对称,0为不对称
int nb(struct freenode *p, struct freenode* q)//传入根结点的左右孩子
{if (p == NULL && q != NULL || p != NULL && q == NULL)//一边为空一边不为空return 0;else if (p == NULL && q == NULL)//两边同时为空return 1;else if (p->data != q->data)//两边都不为空且两边值不相等return 0;//剩下的两边都不为空且值相等还要继续判断int x, y;x = nb(p->lchild, q->rchild);//左结点的左孩子和右结点的右孩子比较y = nb(p->rchild, q->lchild);//左结点的右孩子和右结点的左孩子比较if (x == 1 && y == 1)return 1;elsereturn 0;
}
3二叉树的深度
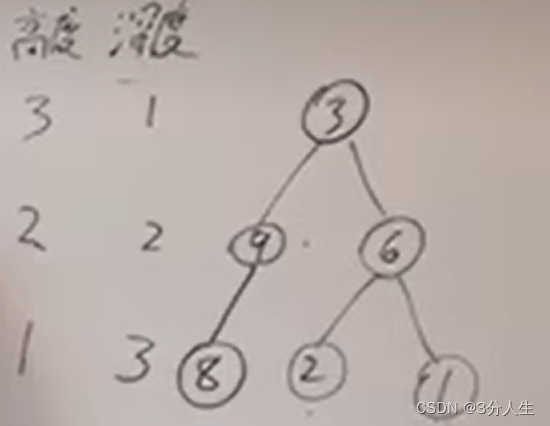
最大深度
思路
采用后序遍历,递归调用并返回每次最大深度
伪代码如下
int nb(struct freenode* T)//传入根结点
{if (T == NULL)//为空返回0return 0;return max(nb(T->lchild), nb(T->rchild)) + 1;//max返回两者较大值
}
最小深度
思路
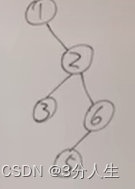
求最小深度并不是将求最大深度的max改成min就行了,首先最小深度是指从根结点到叶子结点的最小值,如果只把求最大值的max改成min按照下面这个图得到的结果为1,而实际结果应该为3,我们知道叶子结点是没有左孩子和右孩子的,求最小深度问题就等价与求叶子结点,所以说在递归返回时如果没有左右孩子就返回零,如果只有其中一个孩子就返回那个孩子的值,如果有两个孩子就返回较小的那个,具体操作看代码
int nb(struct freenode* T)//传入根结点
{if (T->lchild == NULL && T->rchild == NULL)//没有左右孩子返回0return 0;else if (T->lchild != NULL && T->rchild == NULL)//没有右孩子,返回左孩子return nb(T->lchild);else if (T->lchild == NULL && T->rchild != NULL)//没有左孩子,返回右孩子return nb(T->rchild);return min(nb(T->lchild), nb(T->rchild)) + 1;//两个孩子都有,返回较小者
}4二叉树的结点数量
给你一个二叉树,让你求二叉树的结点数量
思路
前序,中序,后序遍历都可以,后序遍历代码相对简洁一点,从根结点传入,按照递归三部曲
1,确定函数参数和返回类型:参数显然就是从根结点传入,我们要去求结点数量,返回的值肯定就是结点数,为int型
2,递归结束的条件:显然就是结点为空时返回0
3,单层递归逻辑:我们要去求结点数量,而每一层递归求得就是左子树结点的数量+右子树结点的数量+这个结点本身
代码如下(后序)
int nb(struct freenode* T)//传入根结点
{if (T == NULL)//为空返回0return 0;//返回左子树结点的数量和右子树结点的数量加上结点本身return nb(T->lchild) + nb(T->rchild) + 1;
}
完全二叉树的结点数量
对于求完全二叉树的结点数量,可以像上面那样用求二叉树结点数量的方法,不过还可以换种方法让代码运行的更快,我们知道一个满二叉树的结点数量为2^n-1(n为二叉树深度),一个完全二叉树按照左右子树递归拆分,肯定会有满二叉树,所以说在递归过程中遇到满二叉树直接返回2^n-1这样就可以节约时间,问题也就转换成如何判断子树为满二叉树了,完全二叉树的子树肯定也是完全二叉树,而判断一个完全二叉树是否为满二叉树,只需要判断二叉树最左下角的那个结点和最右下角的那个结点的深度是否一样。思路讲完上代码
int nb(struct freenode* T)//传入根结点
{if (T == NULL)//为空返回0return 0;struct freenode* left, * right;int sum1 = 1, sum2 = 1;left = T->lchild; right = T->rchild;while (left) //记录最左下角结点的深度{sum1++;left = left->lchild;}while (right)//记录最右下角结点的深度{sum2++;right = right->rchild;}if (sum1 == sum2)return pow(2, sum1) - 1;return nb(T->lchild) + nb(T->rchild) + 1;//返回左子树结点的数量和右子树结点的数量加上结点本身
}
5平衡二叉树
给你一个二叉树,判断二叉树是否为平衡二叉树
思路
平衡二叉树是指二叉树任何结点的左右子树高度差不超过1
判断一个二叉树是否为平衡二叉树也是根据定义来判断的,一个结点的高度是指到叶子结点的距离,求高度采用后序遍历。
代码如下
//-1代表不是平衡二叉树
int nb(struct freenode* T)//传入根结点
{if (T == NULL)//为空返回高度为0return 0;int left = nb(T->lchild);if (left == -1)//只要左子树的子树不为平衡树,那么这个树一定不为平衡树return -1;int right = nb(T->rchild);if (right == -1)//只要右子树的子树不为平衡树,那么这个树一定不为平衡树return -1;if (abs(left - right) > 1)//高度差大于1,不为平衡树返回-1return -1;return max(nb(T->lchild), nb(T->rchild)) + 1;//取左子树和右子树高度的较大值+1为本结点的高度
}
6 中序 后序求前序
已知二叉树的中序和后序遍历结果,求前序遍历

我们知道已知中序,后序可以确定唯一前序遍历结果,中前,中层也可以,前后不能确定唯一的中序
思路
后序遍历中的最后一个数一定是根结点,而在中序遍历中知道根结点是哪一个,又可以大致拆成左右两部分,根据中序拆成两部分又可以把后序拆成两部分,如此反复正是一个递归的过程,
模板题 洛谷P1030 求先序排列
题目描述
给出一棵二叉树的中序与后序排列。求出它的先序排列。(约定树结点用不同的大写字母表示,且二叉树的节点个数 ≤8)。
输入格式
共两行,均为大写字母组成的字符串,表示一棵二叉树的中序与后序排列。
输出格式
共一行一个字符串,表示一棵二叉树的先序。
输入输出样例
输入 #1
BADC BDCA
输出 #1
ABCD
说明/提示
【题目来源】
NOIP 2001 普及组第三题
#include<stdio.h>
#include<string.h>
char a[35], b[35];
void nb(int s1, int r1, int s2, int r2)//分别为中序后序的区间,左闭右开
{if (s1 >= r1)//为空时结束return;int i, j;for (i = s1; i < r1; i++){if (a[i] == b[r2 - 1])//找到根结点,中序遍历拆成两部分{printf("%c", a[i]);break;}}for (j = s2; j < r2; j++){if (r2 - j == r1 - i)//根据中序遍历拆分后序遍历break;}nb(s1, i, s2, j);//递归调用,左半部分nb(i + 1, r1, j, r2-1);递归调用,右半部分return;
}
int main()
{scanf("%s %s", a, b);int k, h;k = strlen(a);h = strlen(b);nb(0, k, 0, h);return 0;
}已知中序,前序求后序,思路大概也是如此,只是根结点为先序的第一个值
相关文章:

二叉树
目录 1翻转二叉树 2对称二叉树 3二叉树的深度 最大深度 最小深度 4二叉树的结点数量 完全二叉树的结点数量 5平衡二叉树 6 中序 后序求前序 二叉树结构体如下: struct freenode {int data;struct freenode *lchild, *rchild;//左孩子 右孩子 }T; 1翻转二…...

边缘计算:挑战与机遇的平衡艺术
前言 边缘计算作为云计算的补充,通过在数据源近处进行数据处理,已经成为实现物联网(IoT)、自动驾驶、智慧城市等应用的重要技术。然而,边缘计算的发展和普及也面临不少挑战,同时也带来了巨大的机遇。 方向…...

Windows11 Copilot助手开启教程(免费GPT-4)
Windows11上开启Copilot助手教程踩坑指南 Copilot介绍Copilot开启步骤1、更新系统2、更改语言和区域3、下载 ViVeTool 工具4、开启Copilot 使用 Copilot介绍 Windows Copilot 是 Windows 11 中的一个新功能,它可以让你与一个智能助理进行对话,获取信息&…...

【Golang入门教程】如何使用Goland创建并运行项目
自然语言处理的发展 文章目录 自然语言处理的发展**前言**创建新项目编辑运行/调试配置编写并运行代码总结强烈推荐专栏集锦写在最后 前些天发现了一个巨牛的人工智能学习网站,通俗易懂,风趣幽默,忍不住分享一下给大家。点击跳转到网站: 人工…...
鸿蒙开发实战-手写文心一言AI对话APP
运行环境 (后面附有API9版本,可修改后在HarmonyOS4设备上运行) DAYU200:4.0.10.16 SDK:4.0.10.15 IDE:4.0.600 在DAYU200:4.0.10.16上运行 一、创建应用 1.点击File->new File->Create Progect 2.选择模版…...

鸿蒙常用UI效果及一些处理方式总结
前言: DevEco Studio版本:4.0.0.600 详细使用介绍 1、Text的一些常用设置 Text(this.message).fontSize(50)//字体大小.fontColor(Color.White)//字体颜色.fontWeight(FontWeight.Bold)//字体加粗.backgroundColor(Color.Black)//背景颜色.fontStyle(…...
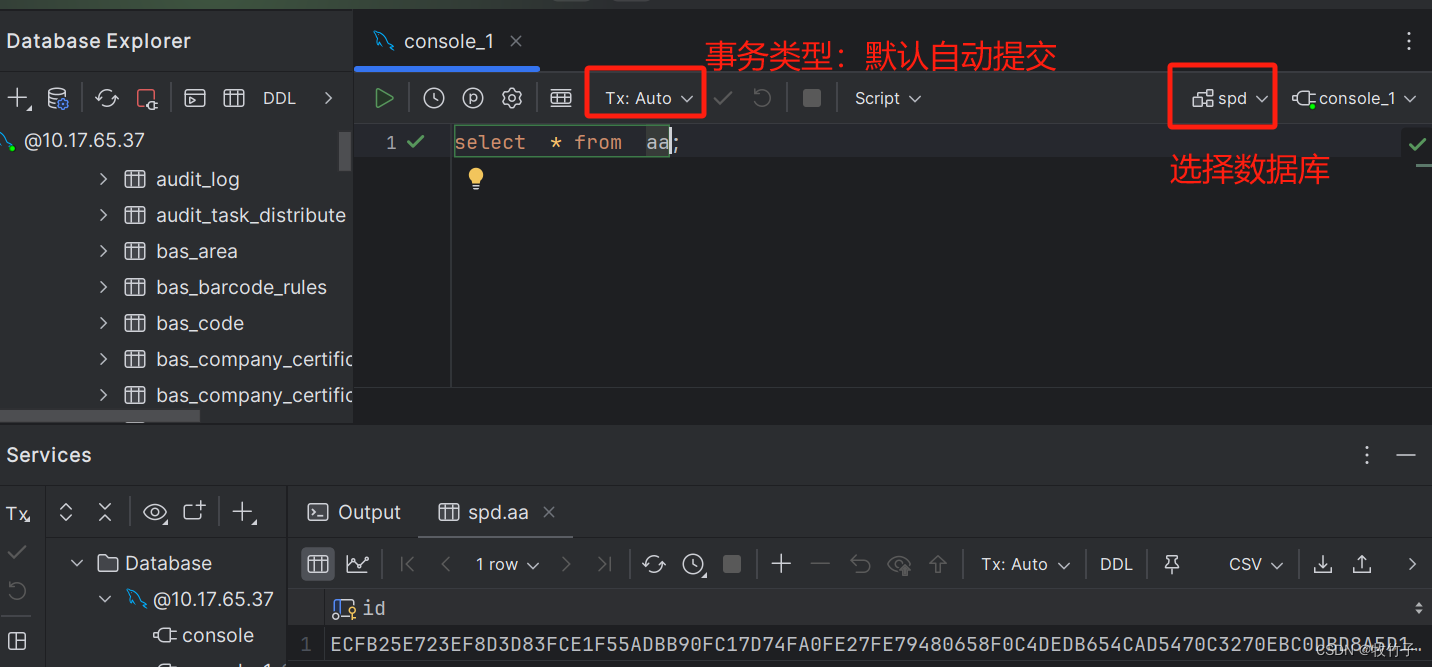
dataGrip连接数据库mysql和intersystems的iris
intersystems公司的产品iris是cache的升级版本,目前绝大多数数据库工具都没法连接这个数据库 datagrip下载地址 https://download-cdn.jetbrains.com.cn/datagrip/datagrip-2023.3.3.exe 选择对应的数据库产品类型 新建数据库资源连接 填上对应的数据库连接和账…...
【51单片机】点亮第一个LED灯
目录 点亮第一个LED灯单片机 GPIO 介绍GPIO 概念GPIO 结构 LED简介软件设计点亮D1指示灯LED流水灯 橙色 点亮第一个LED灯 单片机 GPIO 介绍 GPIO 概念 GPIO(general purpose intput output) 是通用输入输出端口的简称, 可以通过软件来控制…...

ubuntu20.04 格式化 硬盘 扩展硬盘
如何在 Ubuntu 22.04 LTS 上安装分区编辑器 GParted?_gparted安装-CSDN博客 sudo apt install gparted 步骤5:启动GParted 安装完成后,您可以在应用程序菜单中找到GParted。点击它以启动分区编辑器。 通过以上步骤,您可以在Ubun…...

openssl3.2/test/certs - 031 - purpose variants: clientAuth
文章目录 openssl3.2/test/certs - 031 - purpose variants: clientAuth概述笔记END openssl3.2/test/certs - 031 - purpose variants: clientAuth 概述 openssl3.2 - 官方demo学习 - test - certs 笔记 /*! \file my_openssl_linux_log_doc_031.txt \note openssl3.2/tes…...
ubuntu下docker卸载和重新安装
卸载:步骤一:停止Docker服务 首先,我们需要停止正在运行的Docker服务。打开终端,执行以下命令: sudo systemctl stop docker 步骤二:删除Docker安装包 接下来,我们需要删除已经安装的Docker软件…...
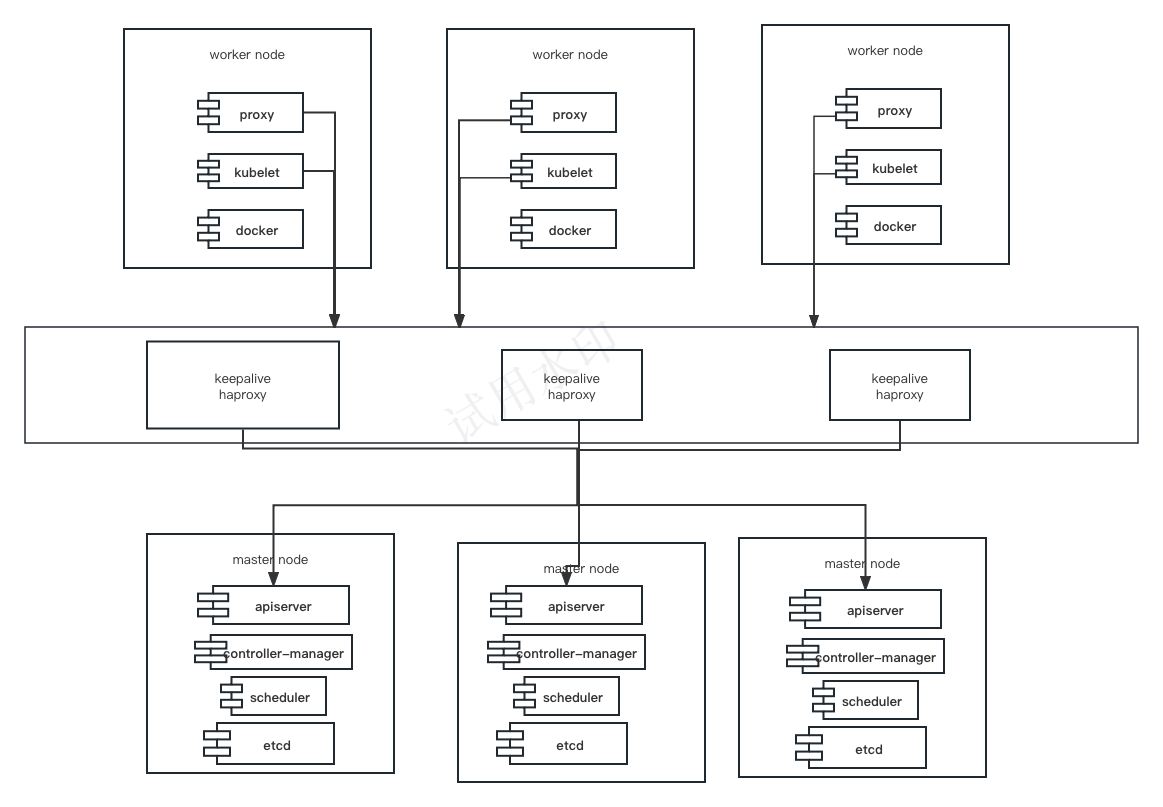
搭建k8s集群实战(一)系统设置
1、架构及服务 Kubernetes作为容器集群系统,通过健康检查重启策略实现了Pod故障自我修复能力,通过调度算法实现将Pod分布式部署,并保持预期副本数,根据Node失效状态自动在其他Node拉起Pod,实现了应用层的高可用性。 …...

go-carbon v2.3.6 发布,轻量级、语义化、对开发者友好的 golang 时间处理库
carbon 是一个轻量级、语义化、对开发者友好的 golang 时间处理库,支持链式调用。 目前已被 awesome-go 收录,如果您觉得不错,请给个 star 吧 github.com/golang-module/carbon gitee.com/golang-module/carbon 安装使用 Golang 版本大于…...

力扣2859-计算k置位下标对应元素的和
计算K置位下标对应元素的和 题目链接 解题思路 对每个下标进行位运算,求得二进制位1的个数,与k进行比较如果相等,证明该元素符合题目要求的值对所有满足要求的值进行累加即可 class Solution { public:int sumIndicesWithKSetBits(vector<…...
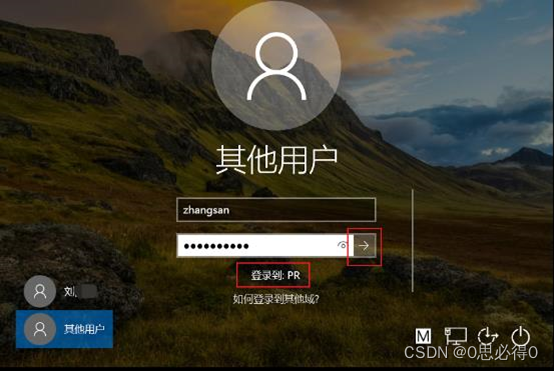
[计算机提升] 切换(域)用户
4.14 切换(域)用户 4.14.1 为什么要切换用户 在Windows系统中,切换用户的主要目的是为了实现多用户共享同一台计算机的便利和安全。当多个人需要使用同一台计算机时,每个人可以登录自己的用户账户,这样可以避免互相干扰和混淆数据。 以下是…...

蓝桥杯练习题dfs与bfs
📑前言 本文主要是【算法】——dfs与bfs的文章,如果有什么需要改进的地方还请大佬指出⛺️ 🎬作者简介:大家好,我是听风与他🥇 ☁️博客首页:CSDN主页听风与他 🌄每日一句ÿ…...

软件游戏提示msvcp140.dll丢失的解决方法,全面分析msvcp140.dll文件
msvcp140.dll是Microsoft Visual C 2015 Redistributable的一部分,它包含了许多用于运行程序的函数和类库。当这个文件丢失或损坏时,依赖于该组件的应用程序可能无法正常启动,系统会弹出错误提示,告知用户找不到msvcp140.dll文件。…...
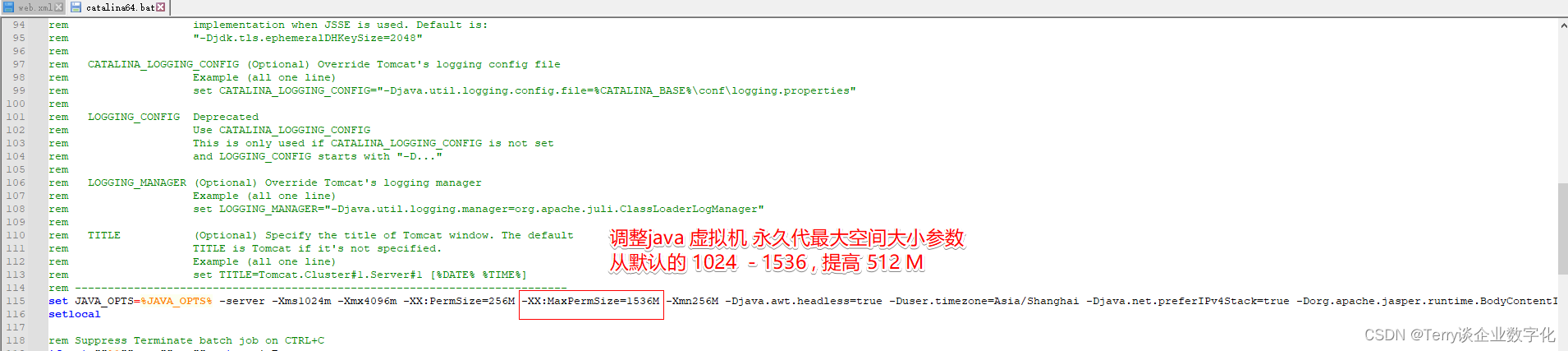
LandrayOA内存调优 / JAVA内存调优 / Tomcat web.xml 超时时间调优实战
目录 一、背景说明 二、LandrayOA / Tomcat 内存调优 2.1 \win64\tomcat\conf\web.xml 文件调优 2.2 \win64\tomcat\bin\catalina64.bat 文件调优 一、背景说明 随着系统的使用时间越来越长,数据量越多,发现系统的有些功能越来越慢&…...

免费SSL数字证书申请,免费数字证书使用教程
为什么要使用SSL数字证书? 1. 数据加密(SSL数字证书通过使用加密算法对传输的数据进行加密,保证数据在传输过程中不被篡改。) 2. 使用了SSL数字证书,浏览器中不会显示不安全,小程序开通,给你的…...
及其使用方法)
深入理解Flutter中的GlobalKey与LocalKey(ValueKey、ObjectKey、UniqueKey)及其使用方法
在Flutter中,Key是一个非常重要的概念,它用于标识和管理Widget。GlobalKey和LocalKey是Key的两个主要子类,而ValueKey、ObjectKey和UniqueKey则是LocalKey的具体实现。在本文中,我们将深入介绍这些关键概念以及它们在Flutter中的使…...

MySQL 隔离级别:脏读、幻读及不可重复读的原理与示例
一、MySQL 隔离级别 MySQL 提供了四种隔离级别,用于控制事务之间的并发访问以及数据的可见性,不同隔离级别对脏读、幻读、不可重复读这几种并发数据问题有着不同的处理方式,具体如下: 隔离级别脏读不可重复读幻读性能特点及锁机制读未提交(READ UNCOMMITTED)允许出现允许…...

Java多线程实现之Callable接口深度解析
Java多线程实现之Callable接口深度解析 一、Callable接口概述1.1 接口定义1.2 与Runnable接口的对比1.3 Future接口与FutureTask类 二、Callable接口的基本使用方法2.1 传统方式实现Callable接口2.2 使用Lambda表达式简化Callable实现2.3 使用FutureTask类执行Callable任务 三、…...

Spring Boot+Neo4j知识图谱实战:3步搭建智能关系网络!
一、引言 在数据驱动的背景下,知识图谱凭借其高效的信息组织能力,正逐步成为各行业应用的关键技术。本文聚焦 Spring Boot与Neo4j图数据库的技术结合,探讨知识图谱开发的实现细节,帮助读者掌握该技术栈在实际项目中的落地方法。 …...

Webpack性能优化:构建速度与体积优化策略
一、构建速度优化 1、升级Webpack和Node.js 优化效果:Webpack 4比Webpack 3构建时间降低60%-98%。原因: V8引擎优化(for of替代forEach、Map/Set替代Object)。默认使用更快的md4哈希算法。AST直接从Loa…...

iview框架主题色的应用
1.下载 less要使用3.0.0以下的版本 npm install less2.7.3 npm install less-loader4.0.52./src/config/theme.js文件 module.exports {yellow: {theme-color: #FDCE04},blue: {theme-color: #547CE7} }在sass中使用theme配置的颜色主题,无需引入,直接可…...

深入理解Optional:处理空指针异常
1. 使用Optional处理可能为空的集合 在Java开发中,集合判空是一个常见但容易出错的场景。传统方式虽然可行,但存在一些潜在问题: // 传统判空方式 if (!CollectionUtils.isEmpty(userInfoList)) {for (UserInfo userInfo : userInfoList) {…...

从面试角度回答Android中ContentProvider启动原理
Android中ContentProvider原理的面试角度解析,分为已启动和未启动两种场景: 一、ContentProvider已启动的情况 1. 核心流程 触发条件:当其他组件(如Activity、Service)通过ContentR…...

Xela矩阵三轴触觉传感器的工作原理解析与应用场景
Xela矩阵三轴触觉传感器通过先进技术模拟人类触觉感知,帮助设备实现精确的力测量与位移监测。其核心功能基于磁性三维力测量与空间位移测量,能够捕捉多维触觉信息。该传感器的设计不仅提升了触觉感知的精度,还为机器人、医疗设备和制造业的智…...
 ----- Python的类与对象)
Python学习(8) ----- Python的类与对象
Python 中的类(Class)与对象(Object)是面向对象编程(OOP)的核心。我们可以通过“类是模板,对象是实例”来理解它们的关系。 🧱 一句话理解: 类就像“图纸”,对…...

游戏开发中常见的战斗数值英文缩写对照表
游戏开发中常见的战斗数值英文缩写对照表 基础属性(Basic Attributes) 缩写英文全称中文释义常见使用场景HPHit Points / Health Points生命值角色生存状态MPMana Points / Magic Points魔法值技能释放资源SPStamina Points体力值动作消耗资源APAction…...
