看图说话:Git图谱解读
很多新加入公司的同学在使用Git各类客户端管理代码的过程中对于Git图谱解读不太理解,我们常用的Git客户端是SourceTree,配合P4Merge进行冲突解决基本可以满足日常工作大部分需要。不同的Git客户端工具对图谱展示会有些许差异,以下是SourceTree中Git图谱演示,后续也会针对类似SourceTree的图谱样式解读进行说明。
图谱拆解
标签 ========(距离相近的标签都有不同颜色,标签对应的分支线与标签颜色一致)
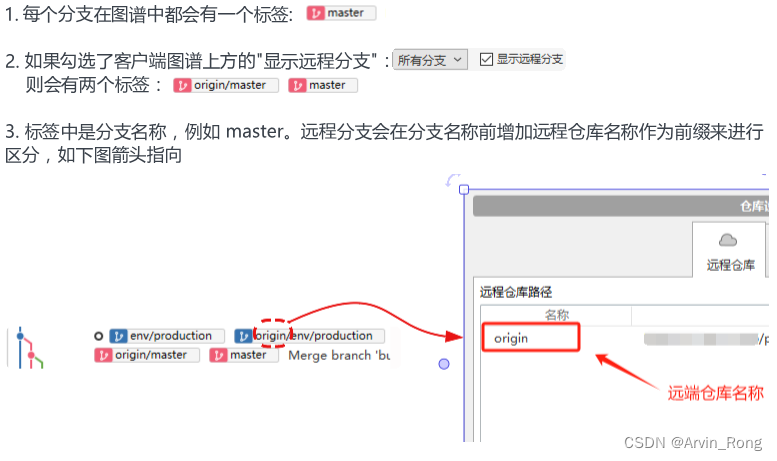
提交(Commit)============================

分支 ======================================
1. 标签所在的Commit是标签对应分支的最新一次提交
2. 可以通过分支对应的本地标签与远程仓库标签位置来判断本地的分支是有代码未推送,还是远程仓库有新的代码未拉取。
分支与提交的关系 ============================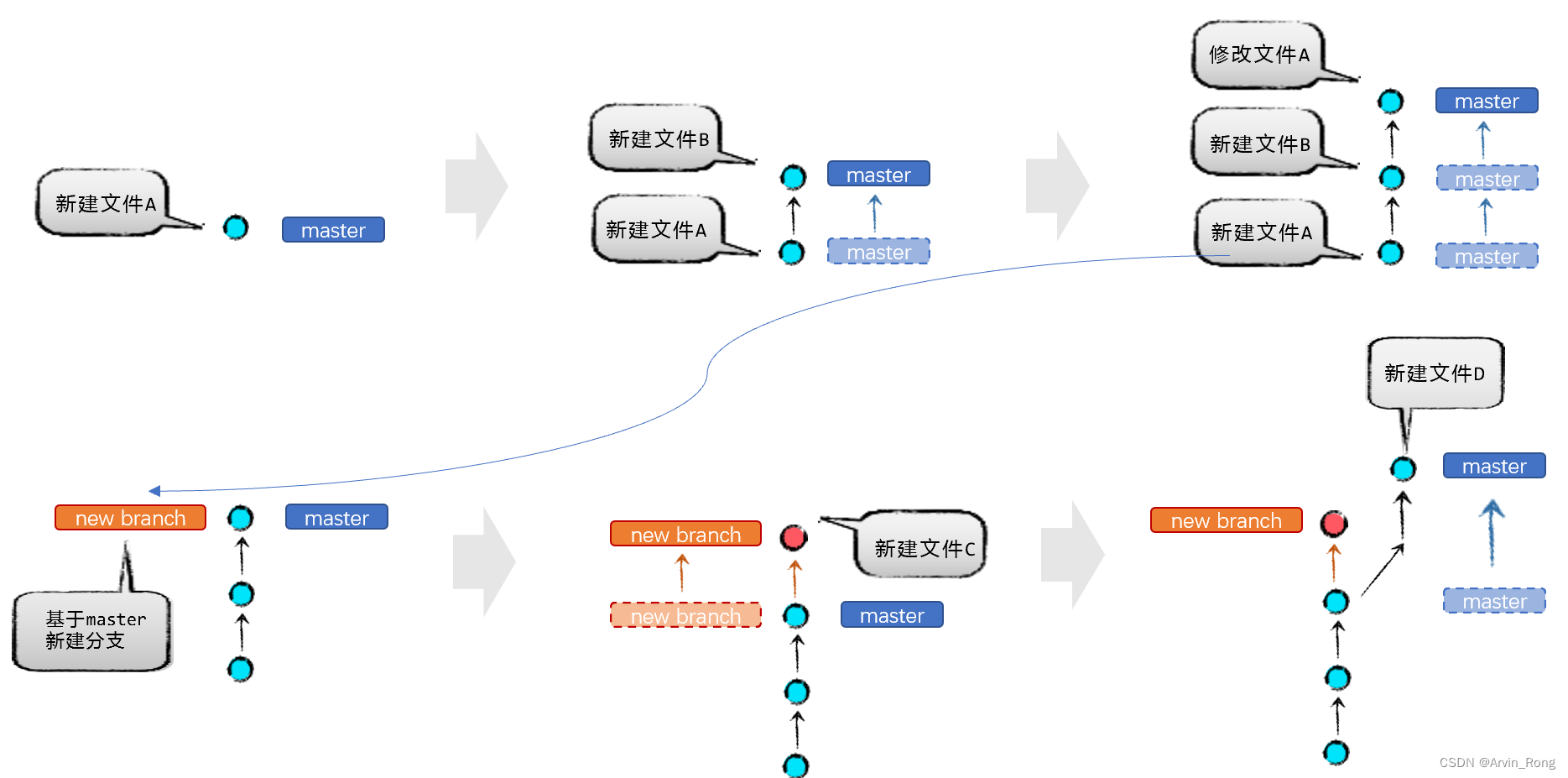
各操作步骤说明
1. 在当前master分支新建一个文件A并提交
2 .在当前master分支新建一个文件B并提交
3. 在当前master分支修改文件A并提交
4. 基于master新建分支 new branch (新建同时会默认切换到新建分支)
5. 在当前new branch分支新建文件C并提交
6. 手动切换到master分支并新建文件D
从上图中能看到每个新的提交会有一个圆点表示,并且新的提交圆点永远在其他的提交上面,不同分支会使用不同的颜色表示,包括线和圆点。在最后一个图的状态下, new branch的内容就是最上一个橘色的圆点和其下三个蓝色圆点的提交内容,master分支的内容则是4个蓝色圆点提交的内容。
分支合并 ===================================
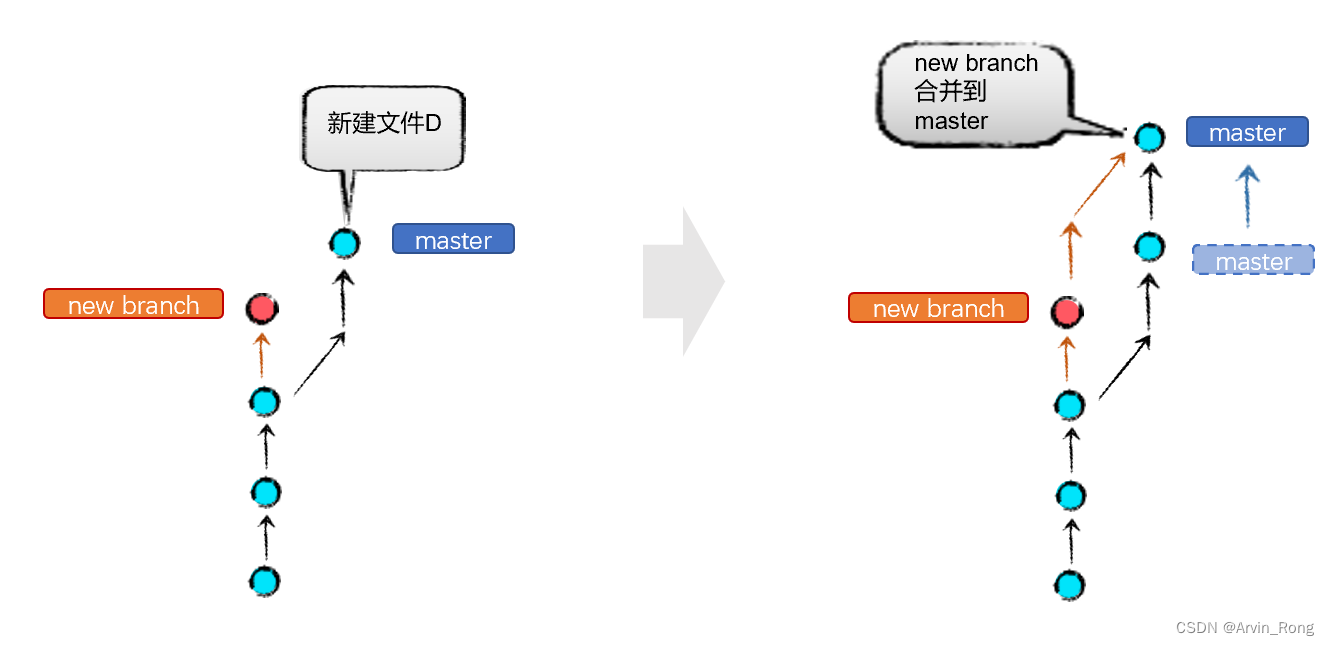
上图描述了把new branch分支合并到master分支时分支和commit的关系,以及图谱中的展示方式。 以上是基于上一段配图中最后一个步骤执行的合并操作,针对一些特定情况下合并后的展示结果会有所有不同,见下一段说明。
分支合并 ====================================
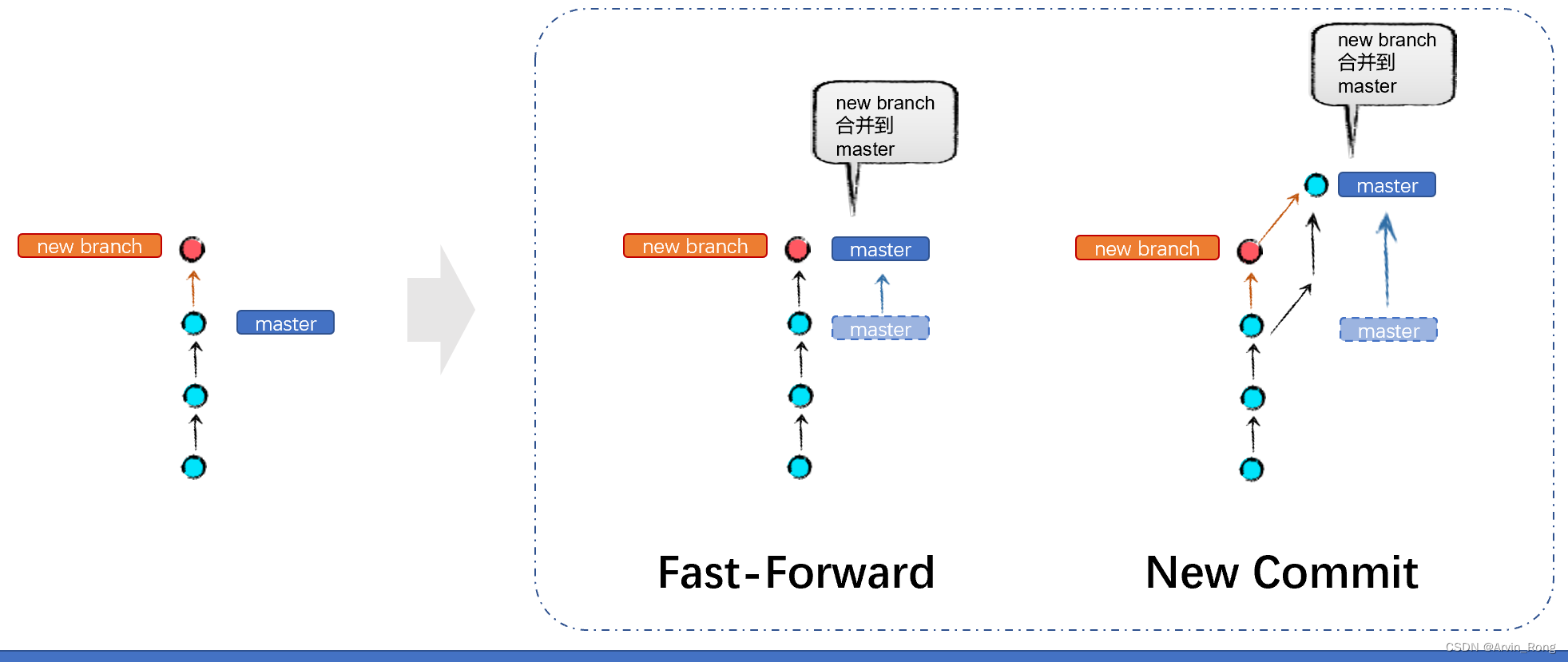
上图左侧展示了new branch和master两个分支的当前状态,然后执行将new branch合并进master的操作,这时因为new branch和master的提交在同一条线上,所以这时候执行合并时有一个fast-forward的方式可以选择,如果选择了fast-forward方式进行合并,实际上是把master分支头部的指针向上移动到new branch指针所在的位置,从图谱中看就是移动了标签,从而完成了合并。如果不选择fast-forward方式,那合并仍然会出现一个拐点会让new branch分支和master分支保持在各自的线上。不使用fast-forward方式进行合并一个好处就是可以从图谱上很明显的看到一个合并的动作,有利于分析分支状态,查看合并操作,防止有时候会忘记我的分支有没有合并过。 关于合并其实还有一种方式叫rebase(变基),这种属于更高级一些的操作用在特定场景,可以保持代码的整洁,将冲突解决提前,避免提交合并审核时出现冲突而需要再次手动解决。
(附)工具界面
相关文章:

看图说话:Git图谱解读
很多新加入公司的同学在使用Git各类客户端管理代码的过程中对于Git图谱解读不太理解,我们常用的Git客户端是SourceTree,配合P4Merge进行冲突解决基本可以满足日常工作大部分需要。不同的Git客户端工具对图谱展示会有些许差异,以下是SourceTre…...

linux新增用户,指定home目录和bash脚本且加入到sudoer列表
前言 近3年一直用自动化脚本,搞得连useradd命令都不会用了。哈哈。 今天还碰到一个问题,有个系统没有‘useradd’和‘passwd’命令,直接蒙了。当然直接用apt install就能安装,不然还得自己编译折腾一会。新建用户 useradd -d /h…...

经典目标检测YOLO系列(三)YOLOV3的复现(1)总体网络架构及前向处理过程
经典目标检测YOLO系列(三)YOLOV3的复现(1)总体网络架构及前向处理过程 和之前实现的YOLOv2一样,根据《YOLO目标检测》(ISBN:9787115627094)一书,在不脱离YOLOv3的大部分核心理念的前提下,重构一款较新的YOLOv3检测器,来对YOLOv3有…...
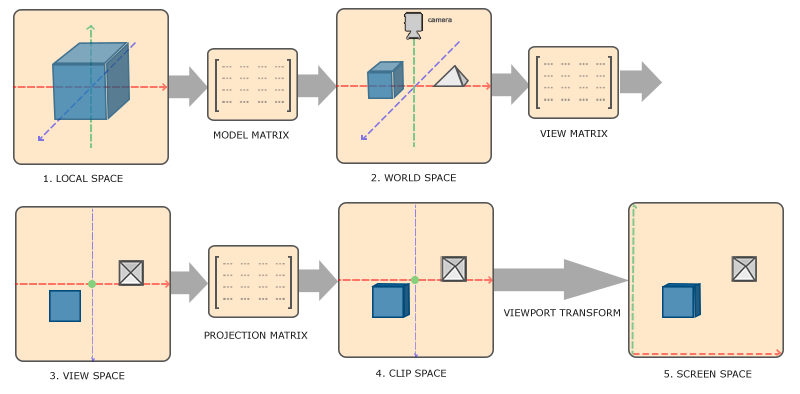
OpenGL/C++_学习笔记(四)空间概念与摄像头
汇总页 上一篇: OpenGL/C_学习笔记(三) 绘制第一个图形 OpenGL/C_学习笔记(四)空间概念与摄像头 空间概念与摄像头前置科技树: 线性代数空间概念流程简述各空间相关概念详述 空间概念与摄像头 前置科技树: 线性代数 矩阵/向量定…...

C语言2024-1-27练习记录
#define _CRT_SECURE_NO_WARNINGS 1#include<stdio.h>//int main() //{ // char c[15] { I, ,a,n,d, ,you,. }; // int i; // for(i 0; i < 15; i) //这个地方有几个地方需要注意一下,首先变量指定之后必须要加上英文状态下的分号 // printf("%c&q…...

深入解析HTTPS:安全机制全方位剖析
随着互联网的深入发展,网络传输中的数据安全性受到了前所未有的关注。HTTPS,作为HTTP的安全版本,为数据在客户端和服务器之间的传输提供了加密和身份验证,从而确保了数据的机密性、完整性和身份真实性。本文将详细探讨HTTPS背后的…...

【197】JAVA8调用阿里云对象存储API,保存图片并获取图片URL地址。
实际工作中,需要用阿里云对象存储保存图片,并且在上传图片到阿里云对象存储服务器后,获取图片在阿里云对象存储服务器的URL地址,以便给 WEB 前端显示。 阿里云对象存储上传图片的工具类 package zhangchao;import com.aliyun.os…...

2024.1.24 C++QT 作业
思维导图 练习题 1.提示并输入一个字符串,统计该字符中大写、小写字母个数、数字个数、空格个数以及其他字符个数 #include <iostream> #include <string.h> #include <array> using namespace std;int main() {string str;cout << "…...
jenkins部署过程记录
一、jenkins部署git链接找不到 原因分析: 机器的git环境不是个人git的权限,所以clone不了。Jenkins的master节点部署机器已经部署较多其他的job在跑,如果直接修改机器的git配置,很可能影响到其他的job clone 不了代码,…...

JS-策略设计模式
设计模式:针对特定问题提出的简洁优化的解决方案 一个问题有多种处理方案,而且处理方案随时可能增加或减少比如:商场满减活动 满50元减5元满100元减15元满200元减35元满500元减100元 // 满减金额计算函数 function count(money, type) {if …...

漏洞复现-EduSoho任意文件读取漏洞(附漏洞检测脚本)
免责声明 文章中涉及的漏洞均已修复,敏感信息均已做打码处理,文章仅做经验分享用途,切勿当真,未授权的攻击属于非法行为!文章中敏感信息均已做多层打马处理。传播、利用本文章所提供的信息而造成的任何直接或者间接的…...

「QT」QString类的详细说明
✨博客主页何曾参静谧的博客📌文章专栏「QT」QT5程序设计📚全部专栏「VS」Visual Studio「C/C++」C/C++程序设计「UG/NX」BlockUI集合「Win」Windows程序设计「...
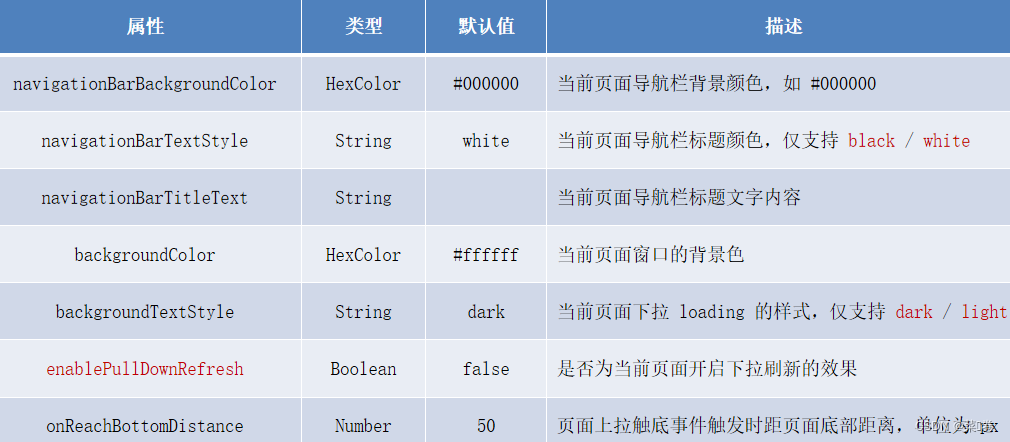
微信小程序-04
rpx(responsive pixel)是微信小程序独有的,用来解决屏适配的尺寸单位。 import 后跟需要导入的外联样式表的相对路径,用 ; 表示语句结束。 定义在 app.wxss 中的样式为全局样式,作用于每一个页面。 在页面的 .wxss 文…...
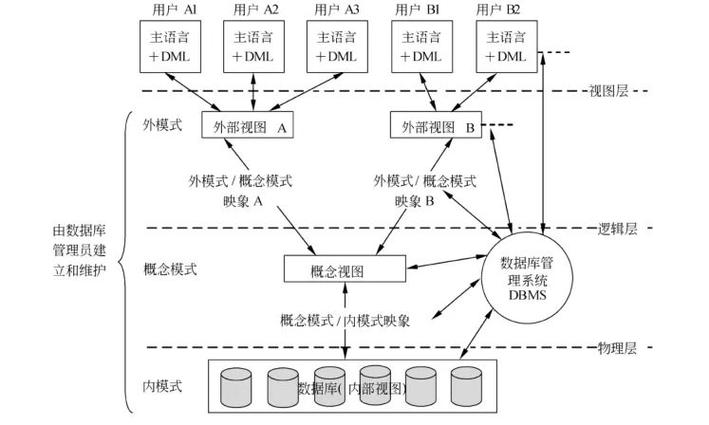
什么是数据库的三级模式两级映象?
三级模式两级映象结构图 概念 三级模式 内模式:也称为存储模式,是数据物理结构和存储方式的描述,是数据在数据库内部的表示方式。定义所有的内部记录类型、索引和文件组织方式,以及数据控制方面的细节。模式:又称概念…...

初识人工智能,一文读懂机器学习之逻辑回归知识文集(6)
🏆作者简介,普修罗双战士,一直追求不断学习和成长,在技术的道路上持续探索和实践。 🏆多年互联网行业从业经验,历任核心研发工程师,项目技术负责人。 🎉欢迎 👍点赞✍评论…...

2024 CKA 题库 | 15、备份还原 etcd
不等更新题库 文章目录 15、备份还原 etcd题目:考点:参考链接:解答:备份快照恢复快照 检查 15、备份还原 etcd 题目: 设置配置环境 此项目无需更改配置环境。但是,在执行此项目之前,请确保您已返回初始节点。 [candidatemaster01] $ exit #…...
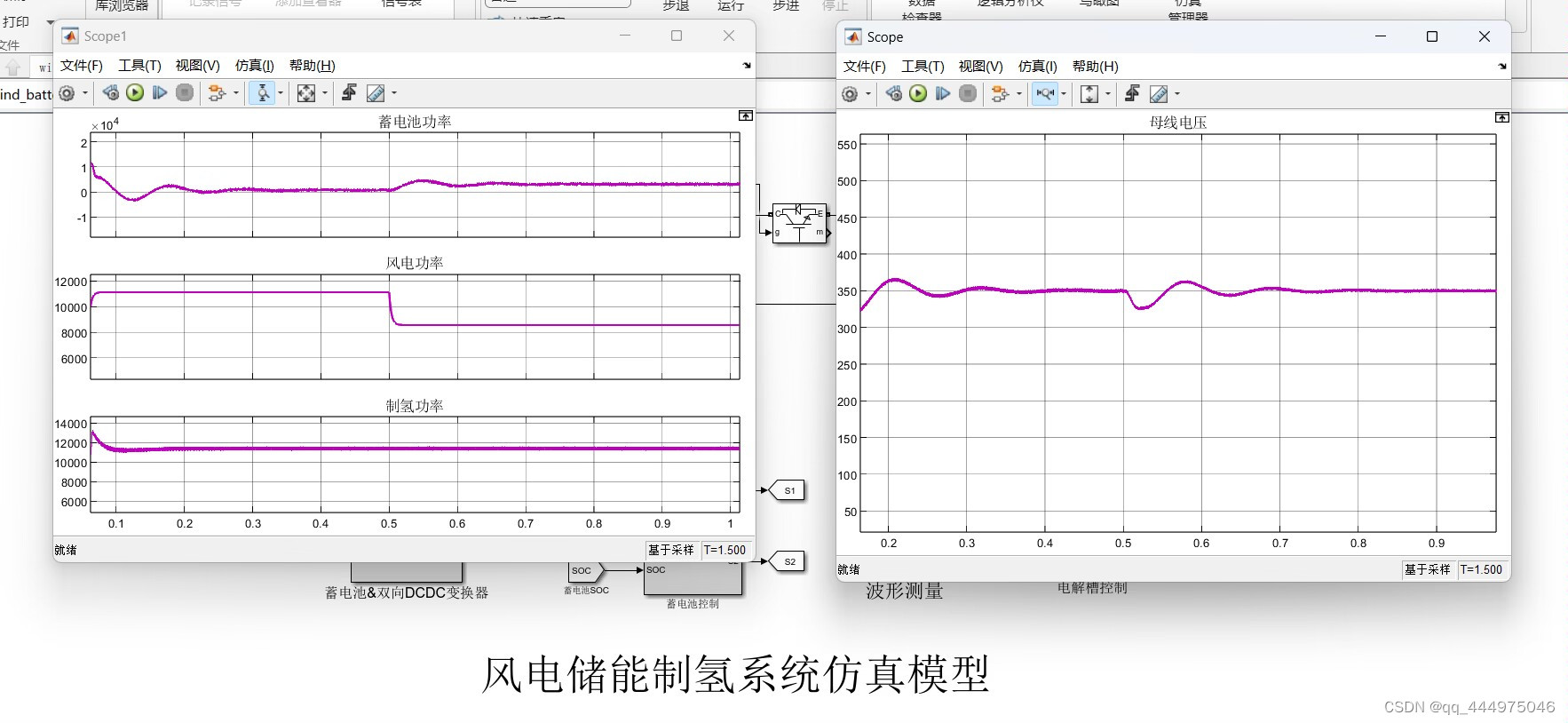
基于Matlab/Simulink直驱式风电储能制氢仿真模型
接着还是以直驱式风电为DG中的研究对象,上篇博客考虑的风电并网惯性的问题,这边博客主要讨论功率消纳的问题。 考虑到风速是随机变化的,导致风电输出功率的波动性和间歇性问题突出;随着其应用规模的不断扩大以及风电在电网中渗透率…...
复习提纲16)
计算机网络(第六版)复习提纲16
三 IP地址与MAC地址 1 IP层只能看到IP数据报 2 路由器只根据目的IP地址进行转发 3 局域网的链路层只能看到MAC帧 4 IP层抽象的互联网屏蔽了下层的复杂细节,在网络层讨论问题能够使用统一的、抽象的IP地址来研究主机和主机或路由间的通信 问题: 1 主机或路…...
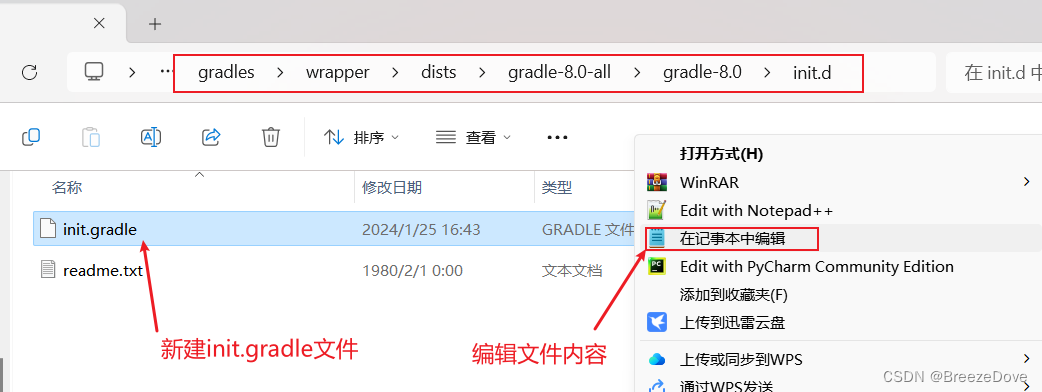
【AndroidStudio】2022.3Giraffe连接超时,更换下载源,使用本地gradle,版本对应问题
记录了使用AndroidStudio2022.3 Giraffe版本在搭建环境时遇到的问题,包括连接超时,gradle无法读取等。 如果只看如何正确的配置,直接跳转第3节 配置汇总 1 连接超时 项目一开始会自动下载gardle文件来加载项目 1.1 Connect timed out 基…...

【Midjourney】内容展示风格关键词
1.几何排列(Geometric) "Geometric" 是一个与几何有关的词汇,通常用于描述与形状、结构或空间几何特征相关的事物。这个词可以涉及数学、艺术、工程、计算机图形学等多个领域。 使用该关键词后,图片中的内容会以平面图形拼接的方式展示&#…...

学习STC51单片机31(芯片为STC89C52RCRC)OLED显示屏1
每日一言 生活的美好,总是藏在那些你咬牙坚持的日子里。 硬件:OLED 以后要用到OLED的时候找到这个文件 OLED的设备地址 SSD1306"SSD" 是品牌缩写,"1306" 是产品编号。 驱动 OLED 屏幕的 IIC 总线数据传输格式 示意图 …...

Java 加密常用的各种算法及其选择
在数字化时代,数据安全至关重要,Java 作为广泛应用的编程语言,提供了丰富的加密算法来保障数据的保密性、完整性和真实性。了解这些常用加密算法及其适用场景,有助于开发者在不同的业务需求中做出正确的选择。 一、对称加密算法…...

PL0语法,分析器实现!
简介 PL/0 是一种简单的编程语言,通常用于教学编译原理。它的语法结构清晰,功能包括常量定义、变量声明、过程(子程序)定义以及基本的控制结构(如条件语句和循环语句)。 PL/0 语法规范 PL/0 是一种教学用的小型编程语言,由 Niklaus Wirth 设计,用于展示编译原理的核…...

【HTTP三个基础问题】
面试官您好!HTTP是超文本传输协议,是互联网上客户端和服务器之间传输超文本数据(比如文字、图片、音频、视频等)的核心协议,当前互联网应用最广泛的版本是HTTP1.1,它基于经典的C/S模型,也就是客…...

Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习)
Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习) 一、Aspose.PDF 简介二、说明(⚠️仅供学习与研究使用)三、技术流程总览四、准备工作1. 下载 Jar 包2. Maven 项目依赖配置 五、字节码修改实现代码&#…...

排序算法总结(C++)
目录 一、稳定性二、排序算法选择、冒泡、插入排序归并排序随机快速排序堆排序基数排序计数排序 三、总结 一、稳定性 排序算法的稳定性是指:同样大小的样本 **(同样大小的数据)**在排序之后不会改变原始的相对次序。 稳定性对基础类型对象…...

R 语言科研绘图第 55 期 --- 网络图-聚类
在发表科研论文的过程中,科研绘图是必不可少的,一张好看的图形会是文章很大的加分项。 为了便于使用,本系列文章介绍的所有绘图都已收录到了 sciRplot 项目中,获取方式: R 语言科研绘图模板 --- sciRplothttps://mp.…...

作为测试我们应该关注redis哪些方面
1、功能测试 数据结构操作:验证字符串、列表、哈希、集合和有序的基本操作是否正确 持久化:测试aof和aof持久化机制,确保数据在开启后正确恢复。 事务:检查事务的原子性和回滚机制。 发布订阅:确保消息正确传递。 2、性…...

软件工程 期末复习
瀑布模型:计划 螺旋模型:风险低 原型模型: 用户反馈 喷泉模型:代码复用 高内聚 低耦合:模块内部功能紧密 模块之间依赖程度小 高内聚:指的是一个模块内部的功能应该紧密相关。换句话说,一个模块应当只实现单一的功能…...

MySQL体系架构解析(三):MySQL目录与启动配置全解析
MySQL中的目录和文件 bin目录 在 MySQL 的安装目录下有一个特别重要的 bin 目录,这个目录下存放着许多可执行文件。与其他系统的可执行文件类似,这些可执行文件都是与服务器和客户端程序相关的。 启动MySQL服务器程序 在 UNIX 系统中,用…...
