LeetCode —— 137. 只出现一次的数字 II


😶🌫️😶🌫️😶🌫️😶🌫️Take your time ! 😶🌫️😶🌫️😶🌫️😶🌫️
💥个人主页:🔥🔥🔥大魔王🔥🔥🔥
💥所属专栏:🔥魔王的修炼之路–C++🔥
如果你觉得这篇文章对你有帮助,请在文章结尾处留下你的点赞👍和关注💖,支持一下博主。同时记得收藏✨这篇文章,方便以后重新阅读。
137. 只出现一次的数字 II
这个题在力扣是中等标签,虽然不等于它很难, 但他绝对不简单,比如这个题虽然单纯做题是很简单,但是规定了时间和空间复杂度,那么就难了起来。
给你一个整数数组 nums ,除某个元素仅出现 一次 外,其余每个元素都恰出现 三次 。请你找出并返回那个只出现了一次的元素。
必须设计并实现线性时间复杂度的算法且使用常数级空间来解决此问题。
示例 1:
输入:nums = [2,2,3,2]
输出:3
示例 2:
输入:nums = [0,1,0,1,0,1,99]
输出:99
提示:
1 <= nums.length <= 3 * 104
-231 <= nums[i] <= 231 - 1
nums 中,除某个元素仅出现 一次 外,其余每个元素都恰出现 三次
下面是错误的写法,没有考虑时间和空间复杂度。
// // //复杂度不行 可能是因为递归层次太深,递归每次都会在栈开空间,最会情况就是开n次
// class Solution {
// public:
// int singleNumber(vector<int>& nums) {
// sort(nums.begin(), nums.end());
// int i = 0;
// if(nums[0] != nums[1])
// return nums[0];
// i += 3;
// while(i < nums.size() - 1)
// {
// if(nums[i] != nums[i + 1])
// return nums[i];
// i += 3;
// }
// return nums.back();
// }
// };
首先sort排序使用的快排,快排一般情况下时间复杂度是NlogN,最坏的话就是 N^2,就这个一般情况来说,NlogN是对数线性复杂度,他介于线性和二次方之间,线性一般指的是O(N)这样子的;对于它的空间复杂度也是不满足的,因为递归造成的空间复杂度也是算的,不过可能实现的快排不是递归,而且库里的sort底层实现也可能不只快排而是几中排序的结合优化版,不过时间复杂度通常就是O(N*logN),至于空间复杂度,O(logN),就和一般情况下的快排一样,递归实现的快排而且是最坏情况的话,那么就是O(N)了。
正确解法
//分别将这些数对应二进制位的1有几个存到整型数组p中,然后分别 % 3,是3的倍数的就没了
class Solution {
public:int singleNumber(vector<int>& nums) {size_t arr[32] = {0};size_t a = 1;int flag = 0;int special = 0;for(auto x: nums)//存1{if(x < 0){if(x == -2147483648)//这样也不行,因为这个形参里面的类型int,最小的负数转为正数就越界了,比如char,最大 127,最小-128{x += 1;special++;}x *= -1;//负数变成补码就反了一下,不适合了。 flag++;}for(int i = 0; i < 32; i++){if(((a << i) & x) != 0){arr[i]++;}}}int num = 0;int system = 31;for(int i = 0; i < 32; i++){if(i == 31){cout << "进来了" << endl;arr[i] %= 3;}if(arr[i] % 3 != 0){num += pow(2, i); }}if(flag % 3 != 0)num *= -1;if(special == 1)num--;return num;}
};
这里面最有价值的是里面没有通过排序,然后找单独数字就是直接开辟一个常量级(32个int)的空间,通过记录这些数二进制位的总位数,然后判断哪个 % 3 不等0,那么该数就是单独的。
有个小问题,如果是负数的话,那么在内存中就是补码,上面写的代码就不适合了,但是数据中可能有负数,所以只能将负数改为正数,这是不影响的,但是有一点,负数最大数的绝对值比正数大1,因为就像char,最大127,最小-128,所以转的时候就爆了,超出int范围。
当然这只是自己的解法,所以有个这个坑,要特殊处理一下,肯定有比这好的方法,但是自己真想不出来了,也不想看题解。
- 博主长期更新,博主的目标是不断提升阅读体验和内容质量,如果你喜欢博主的文章,请点个赞或者关注博主支持一波,我会更加努力的为你呈现精彩的内容。
🌈专栏推荐
😈魔王的修炼之路–C语言
😈魔王的修炼之路–数据结构初阶
😈魔王的修炼之路–C++
😈魔王的修炼之路–Linux
更新不易,希望得到友友的三连支持一波。收藏这篇文章,意味着你将永久拥有它,无论何时何地,都可以立即找到重新阅读;关注博主,意味着无论何时何地,博主将永久和你一起学习进步,为你带来有价值的内容。

相关文章:

LeetCode —— 137. 只出现一次的数字 II
😶🌫️😶🌫️😶🌫️😶🌫️Take your time ! 😶🌫️😶🌫️😶🌫️😶🌫️…...

pnpm、npm、yarn 包管理工具
1、npm 关键词:软件包管理器、命令行工具、一个社区和一个平台 npm(Node Package Manager)是一个用于Node.js环境的软件包管理器。它是一个命令行工具,用于安装、升级、删除和管理JavaScript软件包。npm最初是随同Node.js一起发布…...

微服务知识
1、概念 大型单体应用拆分成多个独立部署运行的微服务(解决并发问题) 2、特点 3、技术栈 4、微服务带来的问题 5、微服务的注册中心 服务注册与发现:微服务实例在启动时会向注册中心注册自己的信息…...

如何在微信搭建私域流量池?
A: ①给客户打标签 添加标签,多维度构建用户画像,精准发送消息。 ②群发信息 选择自定义时间,上传内容 (支持文字,图片) ,一键群发 。 ③建立专属素材库 将常用的话术、图片与文件录入至素材库,员工可随…...

MySQL原理(三)锁定机制(1)综述
一、介绍: 1、锁的本质 业务场景中存在共享资源,多个进程或线程需要竞争获取并处理共享资源,为了保证公平、可靠、结果正确等业务逻辑,要把并发执行的问题变为串行,串行时引入第三方锁当成谁有权限来操作共享资源的判…...

Qt知识点总结
将枚举类型转换为字符串 这里使用的在网络编程中,获取socket状态并显示的时候,遇到的一个问题 #include <QMetaEnum>// 将枚举类型转换为字符串 QMetaEnum metaEnum QMetaEnum::fromType<QAbstractSocket::SocketState>(); const char *c…...
13)
什么是系统工程(字幕)13
0 00:00:00,670 --> 00:00:01,582 如果不加图 1 00:00:01,582 --> 00:00:02,130 怎么加 2 00:00:02,130 --> 00:00:03,225 我们来看一下 3 00:00:03,225 --> 00:00:03,590 你看 4 00:00:03,980 --> 00:00:06,720 右键点这个,添加元素 5 00:00:0…...
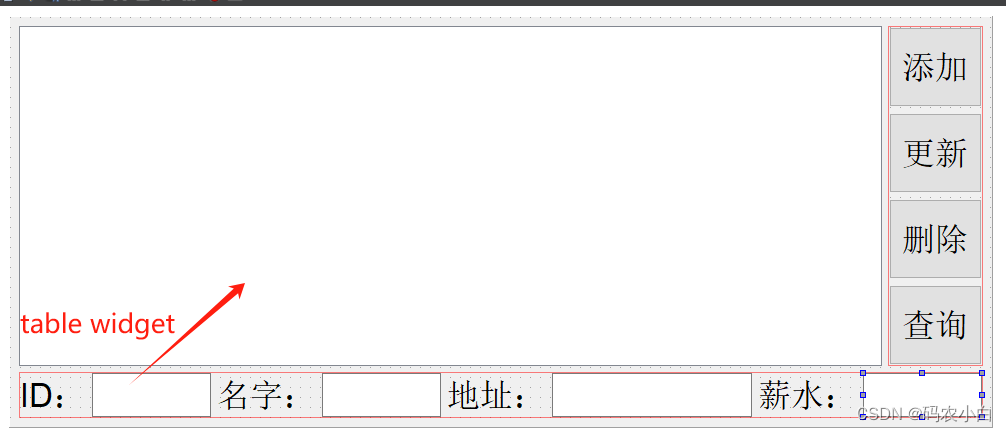
qt学习:Table widget控件
目录 头文件 实战 重新配置ui界面 添加头文件 在构造函数中添加初始化 显示方法 该实例是在sqlite项目上添加qt学习:QTSQL连接sqlite数据库增删改查-CSDN博客 头文件 #include <QTableWidgetItem> 实战 重新配置ui界面 用法介绍,可以双击…...

Android --- Content Provider是使用示例,通俗易懂
当两个应用程序之间需要共享数据时,可以通过 Content Provider 来实现。在这个示例中,我们将创建一个简单的 Content Provider,让 App_B 暴露人口总数的数据,并由 App_A 来获取这个数据。 首先,我们来创建一个简单的示…...

02-opencv简单实例效果和基本介绍-上
机器视觉概述 机器视觉是人工智能正在快速发展的一个分支。简单说来,机器视觉就是用机器代替人眼来做测量和判断。机器视觉系统是通过机器视觉产品(即图像摄取装置,分CMOS和CCD两种)将被摄取目标转换成图像信号,传送给专用的图像处理系统,得到被摄目标的形态信息,根据像素…...
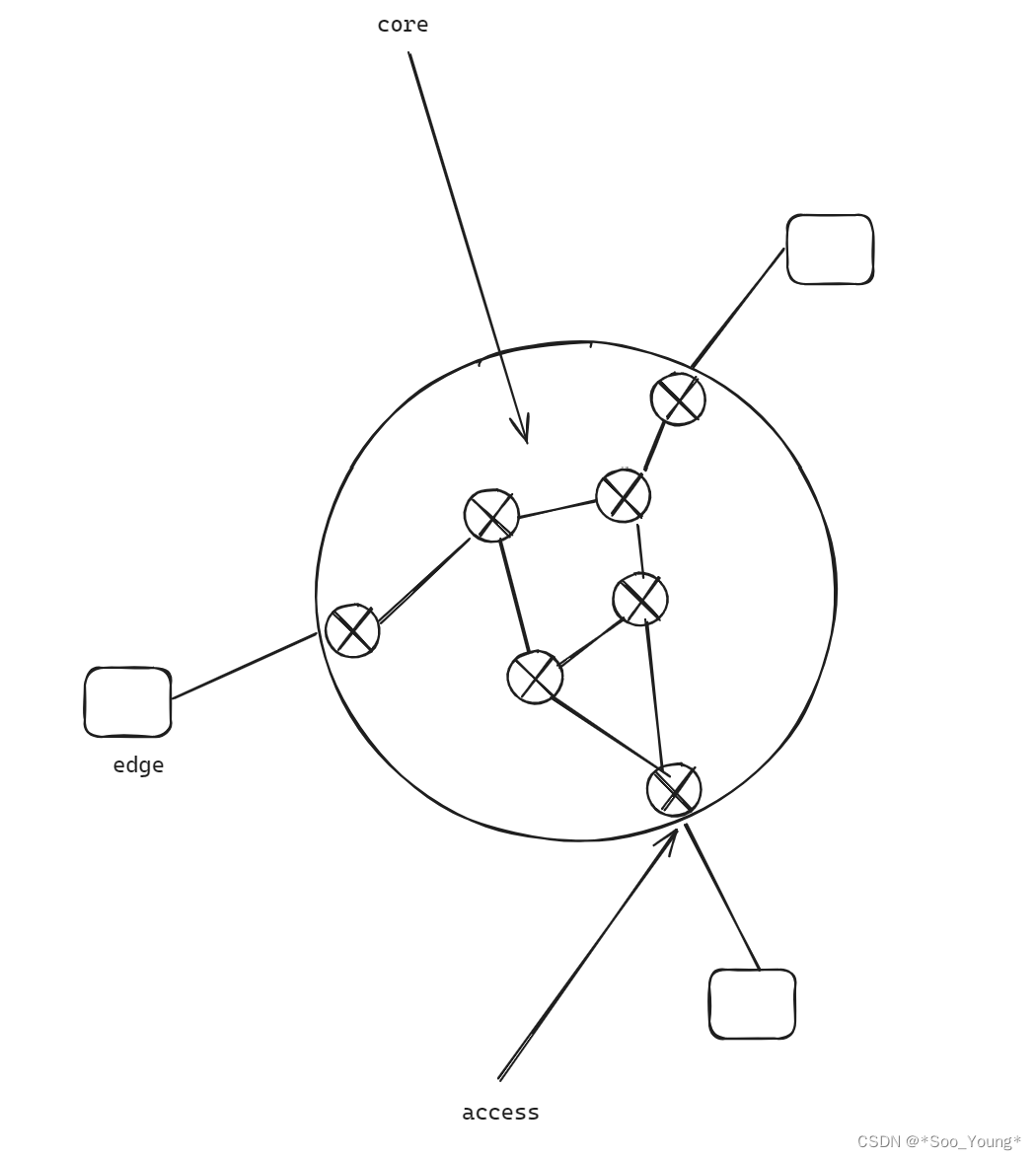
中科大计网学习记录笔记(一):Internet | 网络边缘
计算机网络 前言: 学习视频:中科大郑烇、杨坚全套《计算机网络(自顶向下方法 第7版,James F.Kurose,Keith W.Ross)》课程 该视频是B站非常著名的计网学习视频,但相信很多朋友和我一样在听完前面…...
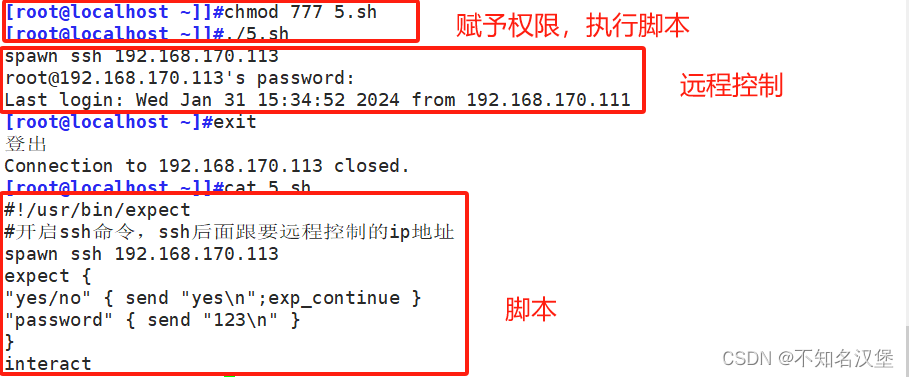
Shell脚本——免交互
目录 一、Here Document免交互 1、免交互概述 2、语法格式 2.1示例:免交互方式实现对行数的统计,将要统计的内容置于标记EOF之间,直接将内容传给wc-l来统计 3、变量设定 ①变量图换成实际值 ②整行内容作为变量并输出结果 ③使输出内…...

【数据分享】1929-2023年全球站点的逐月最高气温数据(Shp\Excel\无需转发)
气象数据是在各项研究中都经常使用的数据,气象指标包括气温、风速、降水、湿度等指标,其中又以气温指标最为常用!说到气温数据,最详细的气温数据是具体到气象监测站点的气温数据! 之前我们分享过1929-2023年全球气象站…...
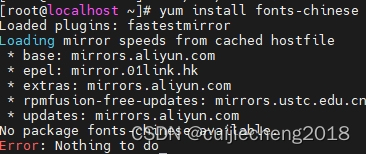
CentOS gui 图形界面显示文字乱码
一、现象 CentOS(CentOS 7.5)控制台下显示中文乱码: 或者通过X11 Forwarding远程显示CentOS的图形化程序文字乱码: 二、解决方法 安装中文语言包: yum install kde-l10n-Chinese 注:网上有些文章会推荐安…...

[Vue入门]Vue的使用:vue对象+data+el+插值表达式
总结性内容: 1.想让Vue工作,就必须创建一个Vue的实例,而且要传入一个配置对象 2.root容器中的代码依然符合html规范,只不过混入了一些特殊的Vue语法 3.root容器里的代码被称为Vue模板 <!DOCtype html> <html><head><meta charset"UTF-8">&l…...

Tomcat运维
目录 一、Tomcat简介 二、系统环境说明 1、关闭防火墙,selinux 2、安装JDK 3、安装Tomcat 三、Tomcat目录介绍 1、tomcat主目录介绍 2、webapps目录介绍 3、Tomcat配置介绍(conf) 4、Tomcat的管理 四、Tomcat 配置管理页面(了解) …...

前端开发基于Qunee绘制网络拓扑图总结-02
1、渲染连线颜色 *关键函数一定要调用:graph.invalidate()* graph.forEach(function(element) {if (element instanceof Q.Edge) {let arr [#549BF1, #AA8A6E, #8F54F1,#5A70BC,#BCBF5C, #BC5A76, #67B4D4,#B4C9EF, #676AD4, #A86EAA,#5CBF7F, #EFB4B4];let inde…...

牛客——中位数图(连续子数组和二维前缀和)
链接:登录—专业IT笔试面试备考平台_牛客网 来源:牛客网 题目描述 给出1~n的一个排列,统计该排列有多少个长度为奇数的连续子序列的中位数是b。中位数是指把所有元素从小到大排列后,位于中间的数。 输入描述: 第一行为两个正…...
Java:搭建eladmin复习mvn、springboot、vue等
目录 1.源码平台后端: 2.源码平台前端: 3.操作系统:centos7.9 4.mysql:5.7.x 安装 5.redis:5.0.X 6.maven:3.8 7.java:1.8: 8.nodejs:16.x 9.通过mvn打包eladmin后端 10.npm打包前端项目进行部署 11.访问测试…...

JavaScript入门
第二个知识点:javascript的基本语法 定义变量 在JavaScript里面,没有int,string 之类的数据类型,只有 var var num 1; var string "天玄地号"; 在javascript中,写完一句语句之后可以不加分号ÿ…...

Frozen-Flask :将 Flask 应用“冻结”为静态文件
Frozen-Flask 是一个用于将 Flask 应用“冻结”为静态文件的 Python 扩展。它的核心用途是:将一个 Flask Web 应用生成成纯静态 HTML 文件,从而可以部署到静态网站托管服务上,如 GitHub Pages、Netlify 或任何支持静态文件的网站服务器。 &am…...

如何在最短时间内提升打ctf(web)的水平?
刚刚刷完2遍 bugku 的 web 题,前来答题。 每个人对刷题理解是不同,有的人是看了writeup就等于刷了,有的人是收藏了writeup就等于刷了,有的人是跟着writeup做了一遍就等于刷了,还有的人是独立思考做了一遍就等于刷了。…...

企业如何增强终端安全?
在数字化转型加速的今天,企业的业务运行越来越依赖于终端设备。从员工的笔记本电脑、智能手机,到工厂里的物联网设备、智能传感器,这些终端构成了企业与外部世界连接的 “神经末梢”。然而,随着远程办公的常态化和设备接入的爆炸式…...

MFC 抛体运动模拟:常见问题解决与界面美化
在 MFC 中开发抛体运动模拟程序时,我们常遇到 轨迹残留、无效刷新、视觉单调、物理逻辑瑕疵 等问题。本文将针对这些痛点,详细解析原因并提供解决方案,同时兼顾界面美化,让模拟效果更专业、更高效。 问题一:历史轨迹与小球残影残留 现象 小球运动后,历史位置的 “残影”…...

为什么要创建 Vue 实例
核心原因:Vue 需要一个「控制中心」来驱动整个应用 你可以把 Vue 实例想象成你应用的**「大脑」或「引擎」。它负责协调模板、数据、逻辑和行为,将它们变成一个活的、可交互的应用**。没有这个实例,你的代码只是一堆静态的 HTML、JavaScript 变量和函数,无法「活」起来。 …...

【实施指南】Android客户端HTTPS双向认证实施指南
🔐 一、所需准备材料 证书文件(6类核心文件) 类型 格式 作用 Android端要求 CA根证书 .crt/.pem 验证服务器/客户端证书合法性 需预置到Android信任库 服务器证书 .crt 服务器身份证明 客户端需持有以验证服务器 客户端证书 .crt 客户端身份…...
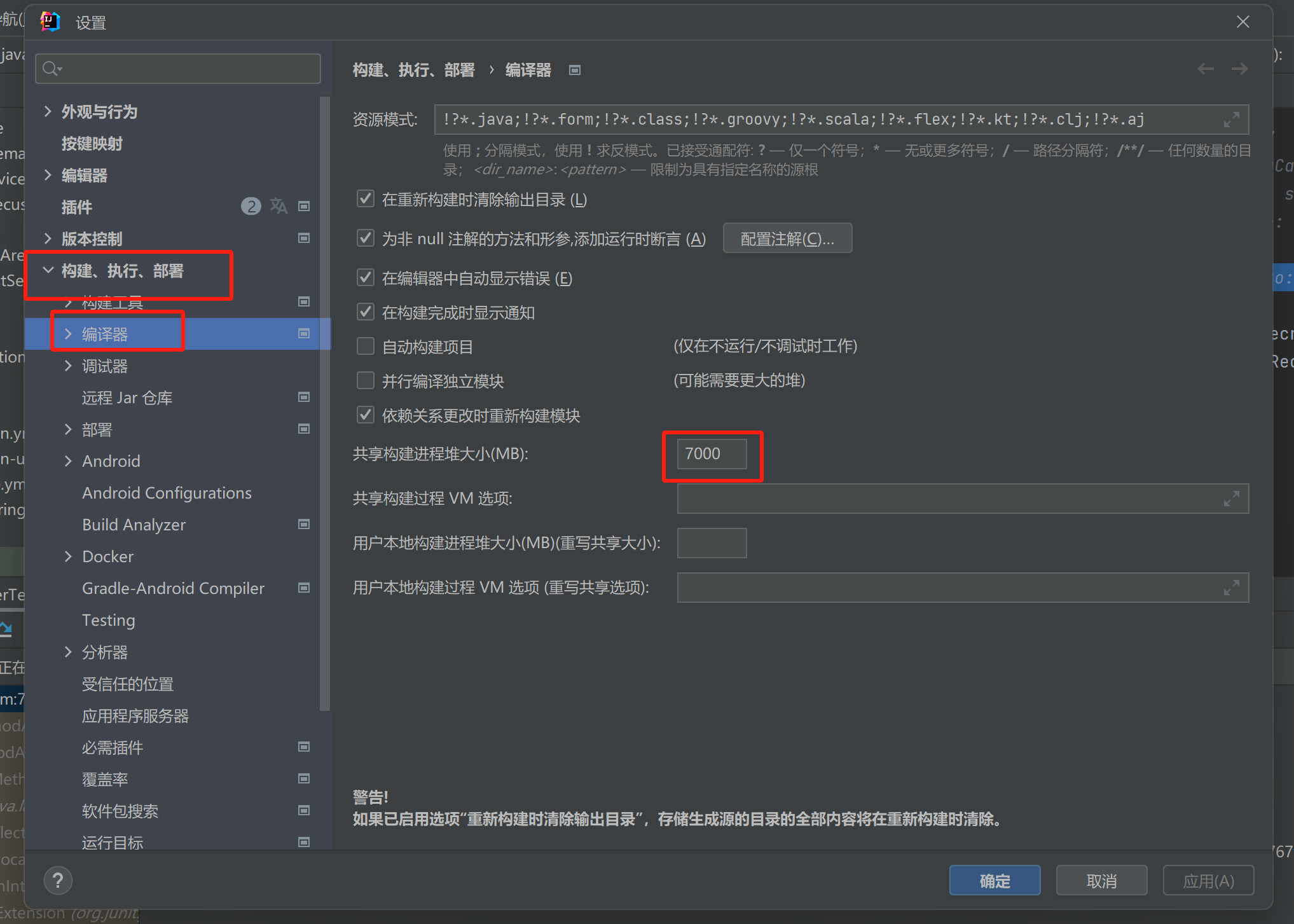
【记录坑点问题】IDEA运行:maven-resources-production:XX: OOM: Java heap space
问题:IDEA出现maven-resources-production:operation-service: java.lang.OutOfMemoryError: Java heap space 解决方案:将编译的堆内存增加一点 位置:设置setting-》构建菜单build-》编译器Complier...

从0开始学习R语言--Day17--Cox回归
Cox回归 在用医疗数据作分析时,最常见的是去预测某类病的患者的死亡率或预测他们的结局。但是我们得到的病人数据,往往会有很多的协变量,即使我们通过计算来减少指标对结果的影响,我们的数据中依然会有很多的协变量,且…...

WinUI3开发_使用mica效果
简介 Mica(云母)是Windows10/11上的一种现代化效果,是Windows10/11上所使用的Fluent Design(设计语言)里的一个效果,Windows10/11上所使用的Fluent Design皆旨在于打造一个人类、通用和真正感觉与 Windows 一样的设计。 WinUI3就是Windows10/11上的一个…...

【AI News | 20250609】每日AI进展
AI Repos 1、OpenHands-Versa OpenHands-Versa 是一个通用型 AI 智能体,通过结合代码编辑与执行、网络搜索、多模态网络浏览和文件访问等通用工具,在软件工程、网络导航和工作流自动化等多个领域展现出卓越性能。它在 SWE-Bench Multimodal、GAIA 和 Th…...
