MATLAB矩阵的操作(第一部分)
矩阵的基本知识
矩阵概念
矩阵(Matrix)在数学中是一个由复数或实数组成的矩形阵列,其元素按照行和列排列。矩阵的定义可以形式化地描述为:
一个 m 行 n 列的矩阵是一个有序的数表,其中包含 m*n 个数,可以表示为: A = [a_{ij}] 或 A = (a_{ij}){m×n}, 这里的 a{ij} 是位于矩阵第 i 行第 j 列的元素,1 ≤ i ≤ m, 1 ≤ j ≤ n。
对于一个具体的 m×n 矩阵 A,例如:
1A =
2| a11 a12 ... a1n |
3| a21 a22 ... a2n |
4| . . . . |
5| . . . . |
6| am1 am2 ... amn |其中,a11、a12,...,amn 分别是矩阵中的每个元素。
更正式地表述:
- 如果一个矩阵有 m 行和 n 列,则称它为一个 m × n 矩阵。
- 当 m = n 时,矩阵 A 称为方阵(Square Matrix),特别地,n阶方阵写作 A_n 或 A^n。
- 若矩阵的元素都是实数,则称该矩阵为实矩阵;若元素均为复数,则称为复矩阵。
同型矩阵
当矩阵A,B的行数和列数都相同时,我们称A,B为同型矩阵。
转置矩阵
转置矩阵(Transpose of a Matrix)是将原矩阵的行和列互换位置得到的新矩阵。对于一个 m×n 的矩阵 A,其转置矩阵记作 Aᵀ 或 AT,是一个 n×m 的矩阵,其中 Aᵀ 的第 i 行、第 j 列的元素等于原矩阵 A 的第 j 行、第 i 列的元素。
具体来说,如果 A 是一个二维数组:
1A = | a11 a12 ... a1n |
2 | a21 a22 ... a2n |
3 | . . ... . |
4 | am1 am2 ... amn |则 A 的转置矩阵 Aᵀ 将会是:
1Aᵀ = | a11 a21 ... am1 |
2 | a12 a22 ... am2 |
3 | . . ... . |
4 | a1n a2n ... amn |数学上表示为:如果 A(i,j) 是原矩阵中位于第 i 行第 j 列的元素,则转置矩阵中的相应元素是 Aᵀ(j,i)。
单位矩阵
单位矩阵(Identity Matrix)是一种特殊的方阵,它在数学和线性代数中扮演着至关重要的角色。单位矩阵通常用 I 或 E 表示,并带有下标来表示其阶数,例如对于一个 n 阶单位矩阵,记为 In 或 En。
单位矩阵的定义如下:
- 它是一个 n×n 的方阵。
- 主对角线(从左上角到右下角)上的所有元素均为 1。
- 其他位置(即非主对角线上的元素)全为 0。
例如,一个 3 阶单位矩阵是这样的:
1I3 = | 1 0 0 |
2 | 0 1 0 |
3 | 0 0 1 |向量的定义
在MATLAB中,向量是一个一维数组,可以包含数值或其他数据类型的元素。定义和创建向量有多种方法:
-
直接输入法:
- 行向量(列数为1):通过将元素用逗号或空格分隔,并放在方括号内来创建行向量。
1rowVec = [1, 2, 3, 4, 5]; % 这是一个行向量 - 列向量(行数为1):通过在元素之间使用分号(
;)而不是逗号来创建列向量。1colVec = [1; 2; 3; 4; 5]; % 这是一个列向量
- 行向量(列数为1):通过将元素用逗号或空格分隔,并放在方括号内来创建行向量。
-
范围生成法:
- 使用冒号(
:)运算符可以快速生成一个等差序列的向量。1seqVec = 1:5; % 生成从1到5的行向量 2seqColVec = [1:5]'; % 生成从1到5的列向量
- 使用冒号(
-
循环构造法:
- 当需要动态地构建向量时,可以使用循环结构。
1N = 5; 2vec = []; % 初始化为空向量 3for i = 1:N 4 vec = [vec, i]; % 或者使用 vec(end+1) = i; 来扩展向量 5end
- 当需要动态地构建向量时,可以使用循环结构。
MATLAB中的向量默认是列优先存储的,也就是说,即使没有明确指定方向,创建一个不包含分号的单行向量也是以列向量的形式存储在内存中。不过,在显示时,MATLAB会根据上下文自动调整输出格式,使得向量看起来像是行向量或列向量。
向量的模的求法
- 计算每个元素的平方。
- 将这些平方值相加。
- 对结果取平方根。
用公式表示为:如果向量 v = [v1, v2, ..., vn],则其模长(欧几里得范数)为:
1||v||_2 = \sqrt{v_1^2 + v_2^2 + ... + v_n^2}矩阵的加减法
注:只有同型矩阵才可以进行加减
-
矩阵加法: 假设有两个同为m×n维的矩阵A和B,要将它们相加,直接在MATLAB命令行或者脚本文件中写入:
1A = [1 2; 3 4]; % 这是一个2x2的示例矩阵A 2B = [5 6; 7 8]; % 这是一个与A相同维度的2x2的示例矩阵B 3C = A + B; % 计算矩阵A和B的和,并将结果存储到C中 -
矩阵减法: 类似地,进行矩阵减法:
1D = A - B; % 计算矩阵A和B的差,并将结果存储到D中
数与矩阵的乘法
在MATLAB中,数(标量)与矩阵的乘法有两种情况:
-
标量乘以矩阵:将一个标量乘到矩阵的所有元素上。例如,假设有一个2x2的矩阵A和一个标量s:
1A = [1 2; 3 4]; % 这是一个2x2的示例矩阵 2s = 2; % 这是一个标量 3 4B = s * A; % 计算标量s与矩阵A的乘积,并将结果存储到B中在这个例子中,B将是:
1B = [2*1 2*2; 2 2*3 2*4] = [2 4; 6 8]; -
矩阵乘以标量:同理,也可以将矩阵乘以一个标量,结果与上述相同。
1C = A * s; % 计算矩阵A与标量s的乘积,并将结果存储到C中此时,C也将是
1C = [2 4; 6 8];
矩阵与矩阵的乘法
在MATLAB中,矩阵与矩阵的乘法遵循特定的规则:前一个矩阵(左侧矩阵)的列数必须等于后一个矩阵(右侧矩阵)的行数。下面给出一个矩阵乘法的例子:
1% 定义两个矩阵 A 和 B
2A = [1 2; 3 4]; % 这是一个2x2的矩阵
3B = [5 6; 7 8]; % 这是一个2x2的矩阵
4
5% 注意:由于矩阵A和B都是2x2的,它们不能直接进行矩阵乘法,因为不符合矩阵乘法的维度要求。
6
7% 为了演示矩阵乘法,我们重新定义一个适合于矩阵乘法的矩阵C:
8C = [1 2; 3 4; 5 6]; % 这是一个3x2的矩阵
9
10D = [7 8 9; 10 11 12]; % 这是一个2x3的矩阵
11
12% 矩阵C和D可以相乘,因为C有2列,而D有2行。
13E = C * D;
14
15% 输出结果
16disp(E);计算结果矩阵E中的每个元素是通过将矩阵C的每一行与矩阵D的每一列对应元素进行逐个相乘并求和得到的。例如:
- E(1,1) = C(1,1)D(1,1) + C(1,2)D(2,1) = 17 + 210 = 27
- E(1,2) = C(1,1)D(1,2) + C(1,2)D(2,2) = 18 + 211 = 26
- E(1,3) = C(1,1)D(1,3) + C(1,2)D(2,3) = 19 + 212 = 33
- ...
- E(3,3) = C(3,1)D(1,3) + C(3,2)D(2,3) = 59 + 612 = 117
所以,整个结果矩阵E就是:
1E = [27 30 33;
2 61 68 75;
3 95 106 117];在这个例子中,由于矩阵C是3x2的,矩阵D是2x3的,所以可以进行矩阵乘法,并得到一个3x3的结果矩阵E。实际计算时,每一个元素e_ij都是通过将矩阵C的第i行与矩阵D的第j列对应元素按顺序逐个相乘然后求和得到的。
但是,如果尝试用原来的矩阵A和B进行矩阵乘法,由于它们都是2x2的矩阵,无法满足矩阵乘法的条件,MATLAB会抛出错误,不允许这样的操作。
注:进行矩阵相乘时。必须满足:前一个矩阵(左矩阵)的列数必须等于后一个矩阵(右矩阵)的行数。也就是说,如果有一个 m×n 的矩阵 A 和一个 n×p 的矩阵 B,则它们可以相乘得到一个 m×p 的矩阵 C。
矩阵的逆
矩阵的逆(Matrix Inverse)是指对于一个方阵(即行数和列数相等的矩阵),如果存在另一个同样大小的矩阵,使得它们相乘的结果是单位矩阵,那么这个矩阵就被称为原矩阵的逆矩阵。
特征值和特征向量
特征值(Eigenvalue): 给定一个 n 阶方阵 A,如果存在非零向量 v 和标量 λ,满足以下关系式:
Av = λv
则称 λ 是矩阵 A 的一个特征值(Eigenvalue),v 称为对应于特征值 λ 的特征向量(Eigenvector)。
换言之,特征值描述了在经过矩阵变换后,特定向量的方向不变但长度按一定比例伸缩的程度。这个特定的比例就是特征值。
特征向量(Eigenvector): 对于一个给定的特征值 λ,其对应的特征向量 v 是一个非零向量,在经过矩阵 A 的作用下,只会发生长度变化而不会改变方向。换句话说,特征向量是在矩阵乘法后仍然保持相同方向(尽管可能有大小变化)的向量。
总结来说,对于矩阵 A 和非零向量 v 以及实数 λ,当 Av = λv 成立时,λ 称为矩阵 A 的特征值,v 称为对应的特征向量。寻找特征值和特征向量的过程通常涉及解一组线性代数方程组。
MATLAB中的向量
在MATLAB中,向量可以被称为一维数组,矩阵可以被称为二维数组
创建方法
在MATLAB中,向量的创建方法主要有三种,分别是:直接输入法、冒号法和利用MATLAB函数创建。下面我们一一来进行介绍:
直接输入法
向量元素需要用中括号“[ ]”括起来,元素之间用空格、逗号、分号或按回车键(Enter键)分隔,就可以创建对应的向量。
若元素之间用空格(可以有多个空格)、逗号分隔,则创建的是行向量;
若用分号、回车键分隔,则创建的是列向量。(注意:这里的逗号和分号都是英文输入法下输入的,不能用中文的逗号或分号)
a = [1 3 5]
a = [1,3,5]
b = [1;3;5]
b = [1
3
5]
冒号法(最常用)
我们可以利用命令:A:step:B 来创建一个行向量。
其中,A是起始值,step是每次递增或递减的步长,B是终止值(不一定刚好停在这里)。若step等于1,则可以直接简写成A:B。
直接看上面的概念不够直观,下面我们举几个例子,大家根据例子来理解会很轻松。
1:2:7 % 每次增加2,直到最后到了7
1:2:8 % 每次增加2,到了7后,如果再增加2的话结果等于9,比8要大,所以到了7就停止了。
0:0.1:1 % 每次增加0.1
0:0.01:1 % 每次增加0.01
1:1:100 % 步长为1时可以省略 1:100
1:10:3 % 从1开始,增加10等于11,比3还要大,所以返回1
5:2:1 % A:step:B 若A > B且步长step > 0,则会返回空的向量
10:-1:6 % 步长为-1,因此会从10开始递减
10:-2:5 % 步长为-2,从10开始递减,到了6后,如果再减去2就等于4,比5还要小,所以到了6就停止了。
10:-100:5 % 步长为-100,因为10-100 = -90比5还要小,所以返回10
10:-10:50 % 若A < B且步长step < 0,则会返回空的向量。
1:0:2 % 若step = 0,则返回空的向量。
补充:
上表中,有三种情况都会导致MATLAB返回空的向量:空的1×0 double行向量。怎么理解这个返回结果呢?这个“1×0”指的是向量的维度,你可以理解为1行0列,即这个向量是空的,不存在元素。在MATLAB中,我们可以直接使用命令[ ]创建空的向量。
[]
利用MATLAB函数创建
linspace函数
两种用法,区别在于是否给定第三个输入参数n,如果我们不指定n,则MATLAB会默认n=100。
linspace(a,b): 该命令用来创建一个行向量,向量中的第一个元素为a,最后一个元素为b,形成总数为100个元素的线性间隔的向量。
linspace (a,b,n): 该命令用来创建一个行向量,向量中的第一个元素为a,最后一个元素为b,形成总数为n个元素的线性间隔的向量。
第一个数为1,最后一个数为100,整个向量构成了一个等差数列,由10个元素组成
linspace(1,100,10) =[1 12 23 34 45 56 67 78 89 100]
第一个数为0,最后一个数为2*pi
linspace(0,2*pi,10)
linspace(1,10) % 如果不指定第三个输入参数n,则默认生成100个元素的等差数列
linspace(100,1,10) % 如果a>b,则步长是负数
linspace (a,b,n)和冒号法a:step:b生成向量的区别
linspace不需要指定步长,MATLAB会根据你给定的元素个数n自动计算出来;而使用冒号法可以自己指定步长。
linspace生成的向量的最后一个元素一定是b,而使用冒号法a:step:b生成的向量的最后元素不一定是b。
循环语句时,冒号法使用的频率最高;而在绘制函数图形时,使用linspace得到的x轴的范围要比冒号法稍微准确一点。例如:我们要绘制sin(x)在区间[0, 2]上的图形,x的范围是0到 2 ,我们使用linspace(0,2*pi)生成的向量的最后一个元素一定是 2 ;如果使用冒号法令x=0:0.1:2*pi,那么x向量的最后一个元素和 2 有一个微小的差异,当然,如果我们将step取得更小,例如取成0.01,那么这个差异几乎可以忽略。
logspace函数(了解即可),
两种常见的用法:
logspace(a,b):创建一个行向量,其第一个元素为10^a,最后一个元素为10^b,形成总数为50个元素的等比数列向量。
logspace(a,b,n):创建一个行向量,其第一个元素为,最后一个元素为,形成总数为n个元素的等比数列向量。
logspace(1,2) % 默认50个元素,linspace函数默认是100个元素
logspace(1,2,10) % 生成第一个数为10^1,最后一个数为10^2,包含10个元素的等比数列
logspace(1,3,5) % 生成第一个元素为10^1,最后一个元素为10^3,包含5个元素的等比数列
logspace(log10(2),log10(1024),10) % 第一个数为2,最后一个数为1024,10个元素组成的等比数列
logspace(2,1,5) % 第一个数为10^2,最后一个数为10^1,5个元素组成的等比数列
向量元素引用
对向量元素的引用(即提取向量指定位置的值)有两种情形,分别是提取向量中的单个元素和提取向量中的多个元素。
向量分为行向量和列向量,它们在MATLAB中只有一个维度,因此我们可以利用向量中包含的元素个数来描述一个向量的大小。
在MATLAB中,向量的索引是从1开始的
在MATLAB中,可以使用length函数或numel函数来计算向量中包含的元素个数。
a = [2 4 8 16 32 64 128 256 512 1024];
length(a) =10
numel(a)=10
单个元素引用
我们提取向量a中单个元素的方法很简单,只需要利用a(ind)命令,小括号中的ind就是你要提取的对应元素的索引。
注:创建向量用中括号,提取元素要用小括号
a = [2 4 8 16 32 64 128 256 512 1024];
a(1)=2 a(9)=512
% a(11) % 索引超出数组元素的数目(10)。
a([]) % 如果是提取空向量的话,结果也为空。
% a(1.5) % a(0) % a(-1) 索引必须为正整数逻辑值
多个元素引用
利用向量的索引来同时提取多个位置的元素,这时候只需要将ind设置成一个向量,ind中放入我们想要提取的元素的索引,然后使用a(ind)命令即可。
a = [2 4 8 16 32 64 128 256 512 1024];
ind = [1 3 5 7 9];
a(ind) %a(ind)=2 8 32 128 512
% 也可以直接简写成:
a([1 3 5 7 9])
% 注意到:1:2:9 = [1 3 5 7 9]
a(1:2:9) % 提取a中奇数位置的元素
% 提取a中偶数位置元素
a(2:2:10)
% 对于同一个位置的元素,我们也可以提取多次
a = [2 4 8 16 32 64 128 256 512 1024];
ind = [1 2 2 3 3 3];
a(ind) % 熟悉的话可以直接写成a([1 2 2 3 3 3])
技巧
使用end索引
假如不知道向量a中有多少个元素,也不使用length函数或者numel函数来计算向量中元素的个数,那提取出a中奇数位置的元素可以用到一个特殊的关键字:end。它有很多种用法,在这里end可以用来替代向量的最后一个索引。
a = [2 4 8 16 32 64 128 256 512 1024];
% 访问a中第五个至最后一个元素,那么我们可以直接使用
a(5:end)
% 我们还可以对end进行计算,例如要访问a中第五个至倒数第三个元素
a(5:end-2)
% 这里有一个易错点,如果使用了end,就不能先将要取元素的索引赋值给ind,然后再调用
ind=5:end a(ind) wrong
a(5:end) yes
% 提取a中奇数位置的元素
a(1:2:end)
问题
将一个向量倒序,例如原向量是[1 5 8 4],倒序后是[4 8 5 1]
a=[1 5 8 4]
b=a(end:-1:1)元素的修改与删除
向量元素的修改
可以直接利用赋值的方法对引用位置的元素进行修改。
a = [2 4 8 16 32 64 128 256 512 1024];
a(1) = 4 % 第一个元素改成4
a([1,3]) = [50 60] % 第1个位置元素改成50;第3个位置元素改成60
% 赋值时,左右两侧的元素个数要相同
% a(1:3) = [5 6] % 无法执行赋值,因为左侧和右侧的元素数目不同。
% 如果右边为常数,则将指定位置的元素全部变成这个常数
a(2:4) = 100 % 第2到4号位置的元素改成100
a(13) = 88
向量元素的删除
如果我们将等号右侧改为空向量[],则可以删除对应位置的元素。
a(1) = [ ] % 删除a的第一个元素
a(end-1:end) = [ ] % 删除a中最后两个元素
思考题:下面哪些语句会报错?
a = [2 4 8 16 32 64 128 256 512 1024];
% a([1,3])
% a(1,3) %提取第一行第三个的元素
% a([2,3])
% a(2,3) %会报错
下面哪些语句会报错?
% a = [2 4 8 16 32];
% a([2,4]) = 5
% a = [2 4 8 16 32];
% a(8) = 10 %a=[2 4 8 16 32 0 0 10]
% a = [2 4 8 16 32];
% a(2,4) = 16 %a=[2 4 8 16 32
0 0 0 16 0]
% a = [2 4 8 16 32];
% a(10) = [] %会报错,矩阵超出索引范围
若有侵权,请联系作者
相关文章:
)
MATLAB矩阵的操作(第一部分)
矩阵的基本知识 矩阵概念 矩阵(Matrix)在数学中是一个由复数或实数组成的矩形阵列,其元素按照行和列排列。矩阵的定义可以形式化地描述为: 一个 m 行 n 列的矩阵是一个有序的数表,其中包含 m*n 个数,可以…...
全面掌握Django的web框架Django Rest_Framework(一)
文章目录 Django Rest_Framework1. DRF介绍2.DRF特点3.环境安装与配置(1)DRF需要以下依赖(2)创建django项目 4.序列化器的使用(1)创建序列化器 5. 反序列化器使用 Django Rest_Framework 1. DRF介绍 Djan…...

AOP+Redisson 延时队列,实现缓存延时双删策略
一、缓存延时双删 关于缓存和数据库中的数据保持一致有很多种方案,但不管是单独在修改数据库之前,还是之后去删除缓存都会有一定的风险导致数据不一致。而延迟双删是一种相对简单并且收益比较高的实现最终一致性的方式,即在删除缓存之后&…...

Hive中left join 中的where 和 on的区别
目录 一、知识点 二、测试验证 三、引申 一、知识点 left join中关于where和on条件的知识点: 多表left join 是会生成一张临时表。on后面: 一般是对left join 的右表进行条件过滤,会返回左表中的所有行,而右表中没有匹配上的数…...

LaTeX教程(001)-LaTeX文档结构(01)
LaTeX教程(001)- LaTeX \LaTeX LATEX文档结构(01) 说在前面 这是我本人学习《The LaTeX Companion》第三版的笔记,但并不是翻译。 书籍的第一章对 LaTeX \LaTeX LATEX及其历史进行了相当长的介绍,这是几乎每一本关于 LaTeX \LaTeX LATEX的书都会…...

SV-7041T 多媒体教学广播IP网络有源音箱
SV-7041T是深圳锐科达电子有限公司的一款2.0声道壁挂式网络有源音箱,具有10/100M以太网接口,可将网络音源通过自带的功放和喇叭输出播放,可达到功率30W。同时它可以外接一个30W的无源副音箱,用在面积较大的场所。5寸进口全频低音喇…...

Linux文本三剑客awk经典案例
前言: AWK是一种专门用于文本处理的编程语言,它被广泛用于数据提取和报告生成,也是企业笔试面试常考的内容,以下34题是awk的用法案例,希望可以帮到你! 1.查看TCP连接状态 [rootnode1 ~]# netstat -nat | a…...
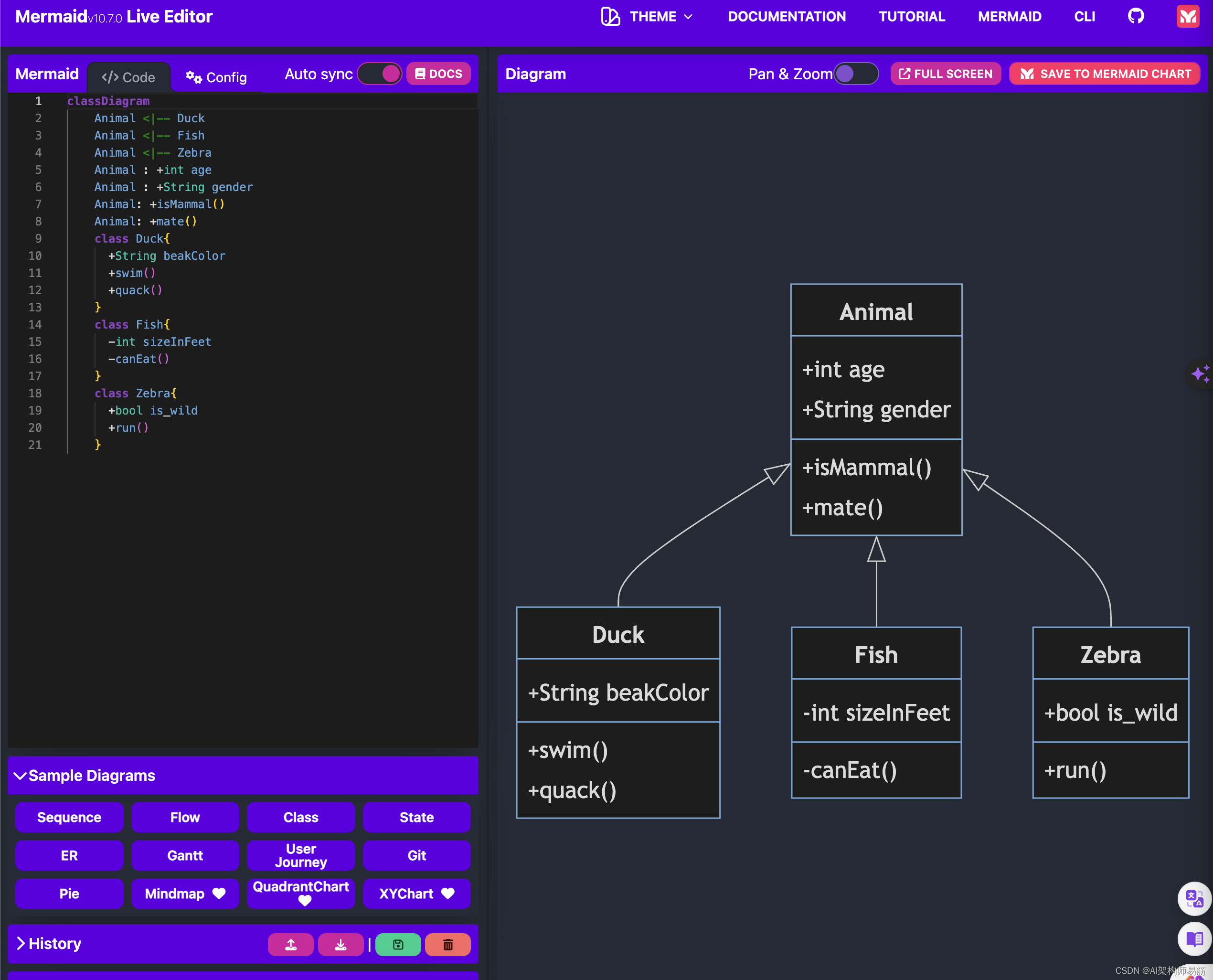
如何使用 Mermaid、GitHub 和 VSCode 用代码创建关系图三
Mermaid 系列 如何使用 Mermaid、GitHub 和 VSCode 用代码创建关系图一如何使用 Mermaid、GitHub 和 VSCode 用代码创建关系图二 1.如何创建甘特图 Gantt 甘特图以条形图的形式用作可视化表示。它有效地展示了项目的时间表,揭示了各个项目组件完成所需的持续时间…...

考研经验总结——政治篇
文章目录 一、前言二、学习情况三、最后 一、前言 不要提前,不要提前,不要提前, 我曾在暑假的时候上了7天左右的政治课,讲真话是很有趣的,并且对于自身的世界观、人生观和价值观的改善也是相当不错的,把我…...
春招秋招,在线测评到底难不难?
现在很多企业在春招的时候,都会有一个在线测评的环节,目的当然就是希望更加了解清楚毕业生的综合能力以及其他方面的素质,好让HR可以根据岗位筛选出能力达标的人才。所以,现在不少即将面对春招的大学毕业生,比较关心的…...

数学建模比赛中,使用大语言模型如chatgpt、文心一言该如何写Prompt(提示)?
在大型语言模型中,"prompt"(中文常译为“提示”或“引导”)是指提供给模型的输入文本,用于指示或引导模型产生特定的输出。它的作用主要是告诉模型用户想要得到什么样的信息或完成什么样的任务。 例如,在使…...

tcpdump 抓包无法落盘
文章目录 问题背景解决办法 问题背景 在嵌入式设备中(Linux系统),为了分析两个网络节点的通讯问题,往往需要用到tcpdump,抓一个.pcap的包在PC端进行分析。博主在实际操作中发现,抓包无法实时落盘。 解决办法 # 下面的命令是写在…...
【网站项目】066农家乐信息平台
🙊作者简介:拥有多年开发工作经验,分享技术代码帮助学生学习,独立完成自己的项目或者毕业设计。 代码可以私聊博主获取。🌹赠送计算机毕业设计600个选题excel文件,帮助大学选题。赠送开题报告模板ÿ…...
idea/webstorm 创建Vue实例 Unresolved type Vue 处理方法
1.电脑本地安装node.js 官网下载 2. 其他: 未排除变量,前期试错(以下步骤配置了,但不确定对解决问题是否有帮助)...

C++ 11新特性之语法甜点2
概述 C 11中引入了许多简化编程工作的语法上的新特性,我们暂且美其名曰:“语法甜点”。书接上篇,我们继续介绍C 11中的这些“语法甜点”,也是第二篇关于“语法甜点”的文章。 语法甜点6:模板右边双括号 在C 03中&#…...

【芯片设计- RTL 数字逻辑设计入门 番外篇 8.1 -- memory repair 详细介绍】
文章目录 memory repair 详细介绍Memory Repair 方法Memory Repair 过程举例memory repair 详细介绍 SoC (System on Chip) 的 Memory Repair 是一种技术,用于检测和修复内存中的损坏单元。由于SoC内部集成了大量的逻辑和存储单元,包括RAM(随机访问存储器)、ROM(只读存储…...
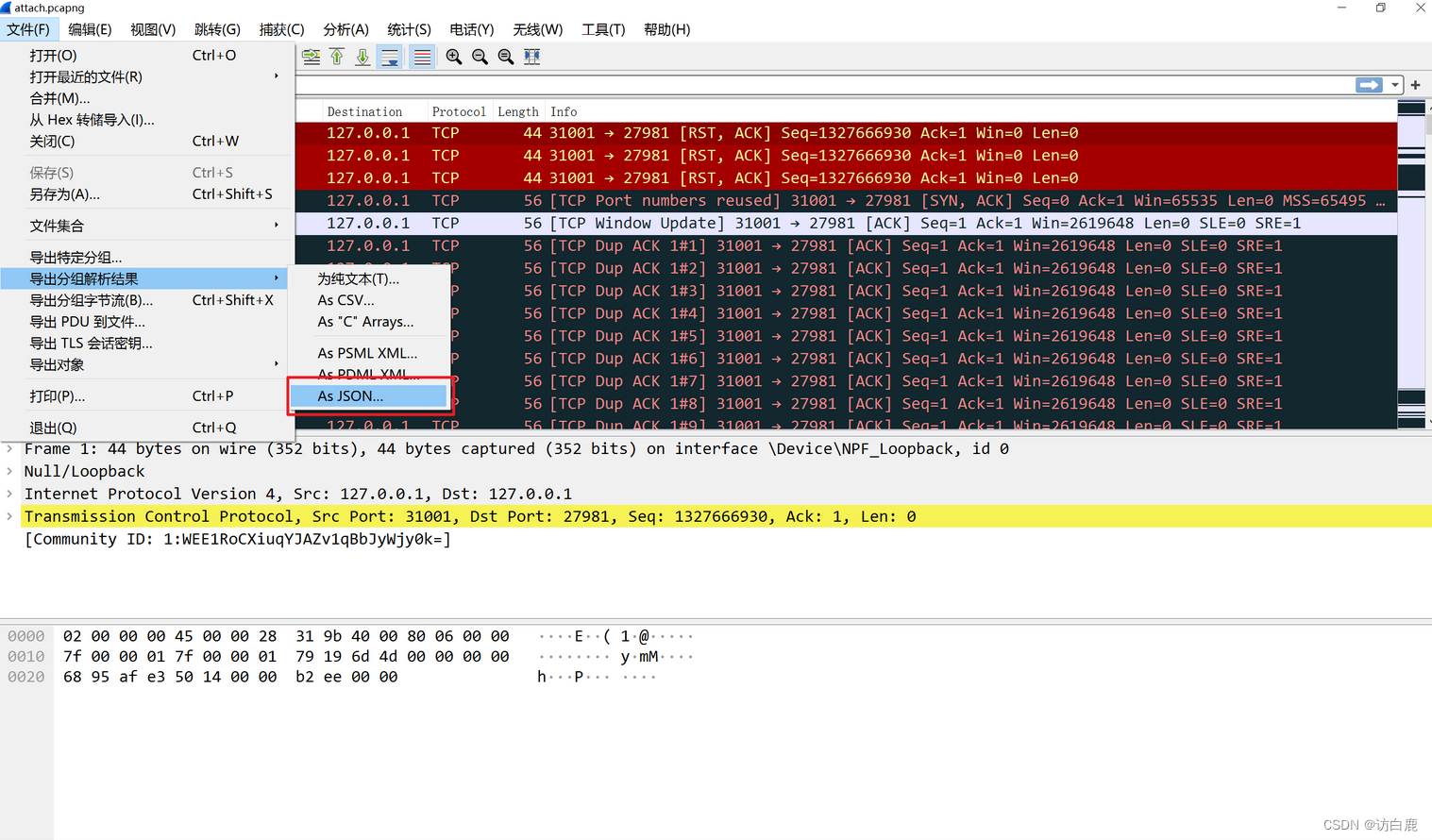
2023强网杯复现
强网先锋 SpeedUp 要求2的27次方的阶乘的逐位之和 在A244060 - OEIS 然后我们将4495662081进行sha256加密 就得到了flag flag{bbdee5c548fddfc76617c562952a3a3b03d423985c095521a8661d248fad3797} MISC easyfuzz 通过尝试输入字符串判断该程序对输入字符的验证规则为9…...

IP代理协议有哪些?爬虫代理如何被合理使用?
随着互联网的普及和发展,IP代理作为一种网络代理方式,越来越受到人们的关注。IP代理协议是网络代理的一种规范,它规定了代理服务器与客户端之间进行通信的规则。了解IP代理协议对于使用代理的人来说非常重要,因为它可以帮助我们更…...
Vue学习笔记(二)快速入门
Vue学习笔记(二)快速入门 vue小试牛刀 hello-vue3.html <body><div id"app"><h1>{{msg}}</h1></div><script type"module">import {createApp} from https://unpkg.com/vue3/dist/vue.esm-b…...

在Vue中@click方法不起效
问题描述: 在跟项目的时候,我们可能会遇到我们click点击时,需要执行多个操作,如:调用方法,修改变量等。举个例子,像这样,我们在管理项目中想要编辑某一值,编辑好后&…...

.Net框架,除了EF还有很多很多......
文章目录 1. 引言2. Dapper2.1 概述与设计原理2.2 核心功能与代码示例基本查询多映射查询存储过程调用 2.3 性能优化原理2.4 适用场景 3. NHibernate3.1 概述与架构设计3.2 映射配置示例Fluent映射XML映射 3.3 查询示例HQL查询Criteria APILINQ提供程序 3.4 高级特性3.5 适用场…...

定时器任务——若依源码分析
分析util包下面的工具类schedule utils: ScheduleUtils 是若依中用于与 Quartz 框架交互的工具类,封装了定时任务的 创建、更新、暂停、删除等核心逻辑。 createScheduleJob createScheduleJob 用于将任务注册到 Quartz,先构建任务的 JobD…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院查看报告小程序
一、开发环境准备 工具安装: 下载安装DevEco Studio 4.0(支持HarmonyOS 5)配置HarmonyOS SDK 5.0确保Node.js版本≥14 项目初始化: ohpm init harmony/hospital-report-app 二、核心功能模块实现 1. 报告列表…...

现代密码学 | 椭圆曲线密码学—附py代码
Elliptic Curve Cryptography 椭圆曲线密码学(ECC)是一种基于有限域上椭圆曲线数学特性的公钥加密技术。其核心原理涉及椭圆曲线的代数性质、离散对数问题以及有限域上的运算。 椭圆曲线密码学是多种数字签名算法的基础,例如椭圆曲线数字签…...
-HIve数据分析)
大数据学习(132)-HIve数据分析
🍋🍋大数据学习🍋🍋 🔥系列专栏: 👑哲学语录: 用力所能及,改变世界。 💖如果觉得博主的文章还不错的话,请点赞👍收藏⭐️留言Ǵ…...

今日学习:Spring线程池|并发修改异常|链路丢失|登录续期|VIP过期策略|数值类缓存
文章目录 优雅版线程池ThreadPoolTaskExecutor和ThreadPoolTaskExecutor的装饰器并发修改异常并发修改异常简介实现机制设计原因及意义 使用线程池造成的链路丢失问题线程池导致的链路丢失问题发生原因 常见解决方法更好的解决方法设计精妙之处 登录续期登录续期常见实现方式特…...

React---day11
14.4 react-redux第三方库 提供connect、thunk之类的函数 以获取一个banner数据为例子 store: 我们在使用异步的时候理应是要使用中间件的,但是configureStore 已经自动集成了 redux-thunk,注意action里面要返回函数 import { configureS…...

佰力博科技与您探讨热释电测量的几种方法
热释电的测量主要涉及热释电系数的测定,这是表征热释电材料性能的重要参数。热释电系数的测量方法主要包括静态法、动态法和积分电荷法。其中,积分电荷法最为常用,其原理是通过测量在电容器上积累的热释电电荷,从而确定热释电系数…...

[免费]微信小程序问卷调查系统(SpringBoot后端+Vue管理端)【论文+源码+SQL脚本】
大家好,我是java1234_小锋老师,看到一个不错的微信小程序问卷调查系统(SpringBoot后端Vue管理端)【论文源码SQL脚本】,分享下哈。 项目视频演示 【免费】微信小程序问卷调查系统(SpringBoot后端Vue管理端) Java毕业设计_哔哩哔哩_bilibili 项…...

Python Einops库:深度学习中的张量操作革命
Einops(爱因斯坦操作库)就像给张量操作戴上了一副"语义眼镜"——让你用人类能理解的方式告诉计算机如何操作多维数组。这个基于爱因斯坦求和约定的库,用类似自然语言的表达式替代了晦涩的API调用,彻底改变了深度学习工程…...
