Codeforces Round 922 (Div. 2)(A~D)补题
A题考虑贪心,要使使用的砖头越多,每块转的k应尽可能小,最小取2,最后可能多出来,多出来的就是最后一块k=3,我们一行内用到的砖头就是 m 2 \frac{m}{2} 2m下取整,然后乘以行数就是答案。
#include <bits/stdc++.h>
#define rep(i,a,b) for(int i = (a); i <= (b); ++i)
#define fep(i,a,b) for(int i = (a); i >= (b); --i)
#define ls p<<1
#define rs p<<1|1
#define PII pair<int, int>
#define ll long long
#define ull unsigned long long
#define db double
#define endl '\n'
#define debug(a) cout<<#a<<"="<<a<<endl;
#define IOS ios::sync_with_stdio(false); cin.tie(0); cout.tie(0);
#define INF 0x3f3f3f3f
#define x first
#define y second
#define int long long
using namespace std;const int N=2e5+10;
vector<int>s[N];
int u[N],ans[N];void solve()
{int n,m;cin>>n>>m;cout<<m/2*n<<endl;
}
signed main()
{IOS
// freopen("1.in", "r", stdin);int t;cin>>t;while(t--)solve();return 0;
}
B题就是猜的一个排序, 对于 i , a [ i ] + b [ i ] 越大我们就考虑将他往后放 , 有一点贪心的思想吧,如果 a [ i ] + b [ i ] 越大放在前面产生的逆序对可能就越多,所以我们考虑将大的往后放 对于i,a[i]+b[i]越大我们就考虑将他往后放,有一点贪心的思想吧,如果a[i]+b[i]越大放在前面产生的逆序对可能就越多,所以我们考虑将大的往后放 对于i,a[i]+b[i]越大我们就考虑将他往后放,有一点贪心的思想吧,如果a[i]+b[i]越大放在前面产生的逆序对可能就越多,所以我们考虑将大的往后放
b题wa了两发,第一次是排序的时候弄反了。
第二次写排序函数的时候降序就写 < 不要写 < = ,写了 < = r e 了 <不要写<=,写了<= re了 <不要写<=,写了<=re了
#include <bits/stdc++.h>
#define rep(i,a,b) for(int i = (a); i <= (b); ++i)
#define fep(i,a,b) for(int i = (a); i >= (b); --i)
#define ls p<<1
#define rs p<<1|1
#define PII pair<int, int>
#define ll long long
#define ull unsigned long long
#define db double
#define endl '\n'
#define debug(a) cout<<#a<<"="<<a<<endl;
#define IOS ios::sync_with_stdio(false); cin.tie(0); cout.tie(0);
#define INF 0x3f3f3f3f
#define x first
#define y second
//#define int long long
using namespace std;const int N=2e5+10;
struct node
{int a,b,sum;
}kk[N];
bool cmp(node t1,node t2)
{return t1.sum<t2.sum;
}
void solve()
{int n;cin>>n;rep(i,1,n) cin>>kk[i].a;rep(i,1,n) cin>>kk[i].b;rep(i,1,n) kk[i].sum=kk[i].a+kk[i].b;sort(kk+1,kk+1+n,cmp);rep(i,1,n) cout<<kk[i].a<<' ';cout<<endl;rep(i,1,n) cout<<kk[i].b<<' ';cout<<endl;}
signed main()
{IOS
// freopen("1.in", "r", stdin);int t;cin>>t;while(t--)solve();return 0;
}
c题是位运算+贪心
一般1e18很可能就是 l o g log log的算法,涉及到异或这些很可能就是要考虑每一位的影响。
这道题就是需要考虑每一位对答案的贡献,这种贡献法也是很常用的思考方式。
赛时有框架了,但是贪心的细节没考虑好没过。
大佬指导的是位运算很多时候需要考虑贪心,因为位与位之间独立。
我们考虑如果a,b两个数的二进制下第i位
当 a i = b i 时无论 x 取何值这一位对答案的贡献都是 0 , 我们就然 x 的这一位为 0 因为 x 要小于 r , x 后面会有用 当a_i=b_i时无论x取何值这一位对答案的贡献都是0,我们就然x的这一位为0因为x要小于r,x后面会有用 当ai=bi时无论x取何值这一位对答案的贡献都是0,我们就然x的这一位为0因为x要小于r,x后面会有用
当 a i ≠ b i 时这时看 x i = 1 是否能然答案变小,如果可以就让 x i = 1 否则就然 x i = 0 当a_i\not=b_i时这时看x_i=1是否能然答案变小,如果可以就让x_i=1否则就然x_i=0 当ai=bi时这时看xi=1是否能然答案变小,如果可以就让xi=1否则就然xi=0
x i = 1 需要建立在 x < r 的前提下 x_i=1需要建立在x<r的前提下 xi=1需要建立在x<r的前提下
#include <bits/stdc++.h>
#define rep(i,a,b) for(int i = (a); i <= (b); ++i)
#define fep(i,a,b) for(int i = (a); i >= (b); --i)
#define ls p<<1
#define rs p<<1|1
#define PII pair<int, int>
#define ll long long
#define ull unsigned long long
#define db double
#define endl '\n'
#define debug(a) cout<<#a<<"="<<a<<endl;
#define IOS ios::sync_with_stdio(false); cin.tie(0); cout.tie(0);
#define INF 0x3f3f3f3f
#define x first
#define y second
#define int long long
using namespace std;const int N=64;int work(int x,int i)
{return x&(1ll<<i);
}void solve()
{int a,b,r;cin>>a>>b>>r;if(a<b) swap(a,b);int ans=0;fep(i,60,0){if(work(a,i)==work(b,i)) continue;if(r>=(1ll<<i)) {int kk=abs(ans+(work(a,i)^(1ll<<i))-(work(b,i)^(1ll<<i)));if(kk<abs(ans)) {ans=kk;r-=(1ll<<i); } else ans+=(work(a,i)^0)-(work(b,i)^0); }else ans+=(work(a,i)^0)-(work(b,i)^0); }cout<<abs(ans)<<endl;
}
signed main()
{IOS
// freopen("1.in", "r", stdin);int t;cin>>t;while(t--)solve();return 0;
}D
二分+大根堆优化dp
首先需要二分答案,在b站的一个up看的讲解b站的up讲解
这种题目就是可以通过二分答案然后变成简单的check。
接下来需要考虑如何check,由于我们删数的位置不确定,同时我们需要求的是在满足一定条件下的最优化问题,这时我们可以考虑一下dp
f [ i ] 表示处理好的前 i 个(前 i 个的区间间隔均 < m i d ) f[i]表示处理好的前i个(前i个的区间间隔均<mid) f[i]表示处理好的前i个(前i个的区间间隔均<mid)
并且删除第 i 个元素,所有删除元素的和的最小值 并且删除第i个元素,所有删除元素的和的最小值 并且删除第i个元素,所有删除元素的和的最小值
考虑转移 : f [ i ] = f [ k ] + a [ i ] , 其中 k 是满足区间和小于 m i d 的 f 中的最小值 考虑转移:f[i]=f[k]+a[i],其中k是满足区间和小于mid的f中的最小值 考虑转移:f[i]=f[k]+a[i],其中k是满足区间和小于mid的f中的最小值
我们可以看到枚举状态 O ( n ) ,枚举转移也需要 O ( n ) , 这样复杂度就是 O ( n 2 l o g n ) 我们可以看到枚举状态O(n),枚举转移也需要O(n),这样复杂度就是O(n^2logn) 我们可以看到枚举状态O(n),枚举转移也需要O(n),这样复杂度就是O(n2logn)
考虑优化可以用优先队列维护和双指针维护满足条件的区间,以及区间内的 f 的最小值 考虑优化可以用优先队列维护和双指针维护满足条件的区间,以及区间内的f的最小值 考虑优化可以用优先队列维护和双指针维护满足条件的区间,以及区间内的f的最小值
由于状态的设计所以状态需要计算到 n + 1 , 因为 n 有删或不删两种情况,这是一个常用的小技巧 由于状态的设计所以状态需要计算到n+1,因为n有删或不删两种情况,这是一个常用的小技巧 由于状态的设计所以状态需要计算到n+1,因为n有删或不删两种情况,这是一个常用的小技巧
#include <bits/stdc++.h>
#define int long long
#define rep(i,a,b) for(int i = (a); i <= (b); ++i)
#define fep(i,a,b) for(int i = (a); i >= (b); --i)
#define ls p<<1
#define rs p<<1|1
#define PII pair<int, int>
#define pll pair<long long, long long>
#define ll long long
#define ull unsigned long long
#define db double
#define endl '\n'
#define debug(a) cout<<#a<<"="<<a<<endl;
#define IOS ios::sync_with_stdio(false); cin.tie(0); cout.tie(0);
#define INF 0x3f3f3f3f
#define x first
#define y secondusing namespace std;const int N=1e5+10;
int n,a[N],f[N];bool check(int x)
{priority_queue<pll,vector<pll>,greater<pll>>q;int l=0,ss=0;q.push({0,0});rep(i,1,n+1){while(l<i&&ss>x) {ss-=a[l];l++;}while(q.size()&&q.top().y<l-1) q.pop();f[i]=q.top().x+a[i];q.push({f[i],i});ss+=a[i]; }return f[n+1]<=x;
}void solve()
{cin>>n;rep(i,1,n) cin>>a[i];a[n+1]=0;int l=0,r=1e15;while(l<r){int mid=(l+r)>>1;if(check(mid)) r=mid;else l=mid+1;}cout<<l<<endl;rep(i,0,n+1) f[i]=0;
}
signed main()
{IOS
// freopen("1.in", "r", stdin);int t;cin>>t;while(t--)solve();return 0;
}
相关文章:
(A~D)补题)
Codeforces Round 922 (Div. 2)(A~D)补题
A题考虑贪心,要使使用的砖头越多,每块转的k应尽可能小,最小取2,最后可能多出来,多出来的就是最后一块k3,我们一行内用到的砖头就是 m 2 \frac{m}{2} 2m下取整,然后乘以行数就是答案。 #inclu…...
Seata下载与配置、启动
目录 Seata下载Seata配置启动Seata Seata下载 首先,我们需要知道我们要使用哪个版本的seata,这就要查看spring-cloud-alibaba版本说明,找到我们对应的seata。 spring-cloud-alibaba版本说明: 地址链接 下面是部分版本说明: s…...
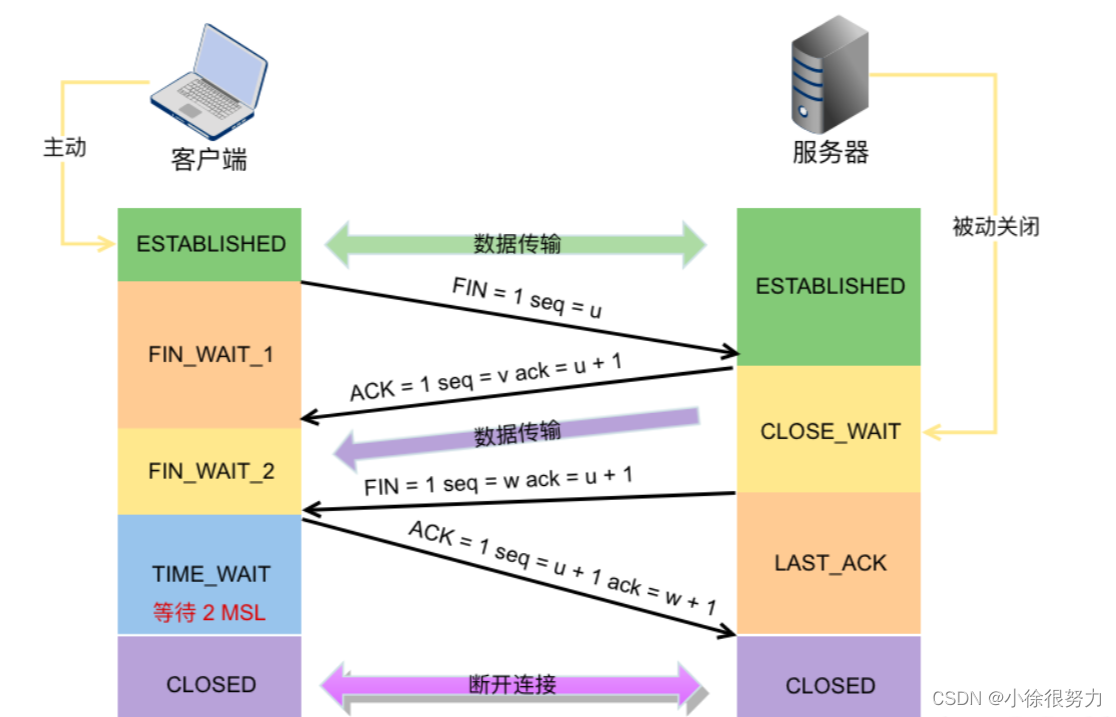
什么是TCP三次握手、四次挥手?
1、三次握手 你(客户端)给一个朋友(服务器)打电话,告诉他你想开始对话。这就像是发送一个SYN(同步序列编号)信号,表示你想开始建立连接。(client向server发送syn,seqx,此时client验证client发送能力正常。client置为SYN SENT状态)…...

C++程序在开机自启和定时器执行时遇到的问题和解决方法
遇到的错误如下: Camera is created.load vfvlog.[dll/so] failed for dll[/vfvlog.so] unexistedLoadDbgConfig, LoadFile fail, err:-3, errno: No such file or directoryqt.qpa.xcb: could not connect to displayqt.qpa.plugin: Could not load the Qt platfo…...

R17 extended DRX(eDRX)
根据工业无线传感器的要求,电池至少可持续使用数年。 在NB-IoT和LTE eMTC中,也有类似的要求。 为了满足极长电池寿命的要求,NB-IoT和LTE eMTC在Release 13中为RRC IDLE UE引入了扩展DRX,在Release 16中为RRC INACTIVE UE引入了eDRX,上面是LTE 引入eDRX的背景。 一 概述 到…...

Debezium发布历史102
原文地址: https://debezium.io/blog/2021/02/24/debezium-1-5-beta1-released/ 欢迎关注留言,我是收集整理小能手,工具翻译,仅供参考,笔芯笔芯. Debezium 1.5.0.Beta1 发布 2021 年 2 月 24 日 作者: Gu…...

探索自然语言处理在改善搜索引擎、语音助手和机器翻译中的应用
文章目录 每日一句正能量前言文本分析语音识别机器翻译语义分析自然语言生成情感分析后记 每日一句正能量 努力学习,勤奋工作,让青春更加光彩。 前言 自然语言处理(NLP)是人工智能领域中与人类语言相关的重要研究方向,…...

echarts:获取省、市、区/县、镇的地图数据
目录 第一章 前言 第二章 获取地图的数据(GeoJSON格式) 2.1 获取省、市、区/县地图数据 2.2 获取乡/镇/街道地图数据 第一章 前言 需求:接到要做大屏的需求,其中需要用echarts绘画一个地图,但是需要的地图是区/县…...

Java_简单模拟实现ArrayList_学习ArrayList
文章目录 一、 了解线性表和顺序表区别1.线性表2.顺序表 二、模拟实现1.定义接口2.定义MyArrayList3.成员变量以及构造方法4.实现打印数组5.实现add方法6.实现查找某个数是否存在contains或者某个数的下标indexOf7.获取或更改pos位置的值 get和set8.获取数组大小 size9.删除某个…...
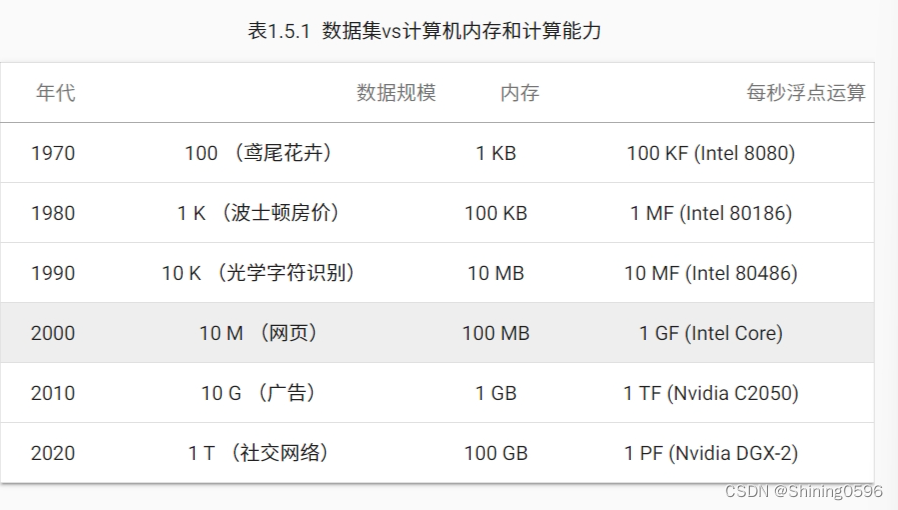
动手学深度学习(一)深度学习介绍2
目录 二、起源 三、深度学习的成功案例: 四、特点: 五、小结: 二、起源 为了解决各种各样的机器学习问题,深度学习提供了强大的工具。 虽然许多深度学习方法都是最近才有重大突破,但使用数据和神经网络编程的核心思…...
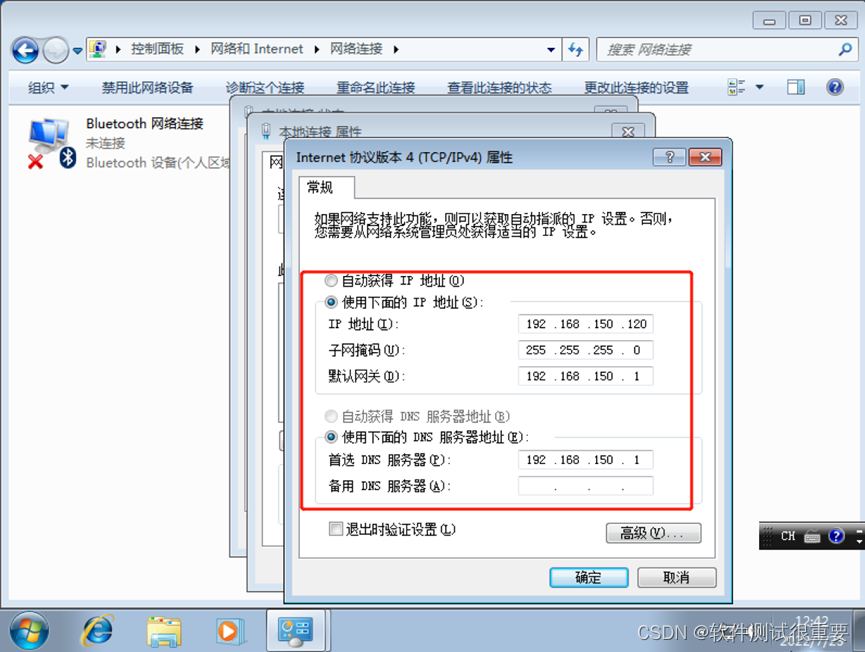
vmware网络配置,VMware的三种网络模式详解与配置
vmware为我们提供了三种网络工作模式 vmware为我们提供了三种网络工作模式, 它们分别是: Bridged(桥接模式)、NAT(网络地址转换模式)、Host-Only(仅主机模式)。 VMware虚拟机的三种网络类型的适用场景如下…...

【Ubuntu】安装hbase
前提 需要安装java 安装 HBase 下载并解压 HBase 安装包: wget https://dlcdn.apache.org/hbase/2.5.7/hbase-2.5.7-bin.tar.gz tar -zxvf hbase-2.5.7-bin.tar.gz配置 HBase 环境变量: export HBASE_HOME/path/to/hbase-2.5.7 export PATH$PATH:$H…...

ubuntu16.04环境轻松安装和应用opencv4.9.0(基于源码编译)
目录 一、环境准备 1、安装cmake 2、安装依赖 3、从github上下载opencv4.9.0.zip 二、安装opencv4.9.0 1、解压4.9.0.zip 2、进入build目录编译 3、安装编译好的相关库 4、修改opencv配置文件并使其生效 5、添加PKG_CONFIG路径,并使其生效 三、opencv环境…...
FastBee开源物联网平台2.0开源版发布啦!!!
一、项目介绍 物美智能(wumei-smart)更名为蜂信物联(FastBee)。 FastBee开源物联网平台,简单易用,更适合中小企业和个人学习使用。适用于智能家居、智慧办公、智慧社区、农业监测、水利监测、工业控制等。 系统后端采用Spring boot;前端采用…...

【NeRF和NLP】一些观察感悟,碎碎念
NeRF的paper,有几个感想: NeRF读的时候感觉和diffusion思路特别像,训练目标是一个很小很小的子步骤,大大简化了训练难度NeRF建模的是“真实”世界,其用模型隐含的存储了真实世界的体素(场)模型…...

Python程序设计 基础数据类型
1.1 编程规范 注释 python注释也有自己的规范,在文章中会介绍到。注释可以起到一个备注的作用,团队合作的时候,个人编写的代码经常会被多人调用,为了让别人能更容易理解代码的通途,使用注释是非常有效的。 在说规范…...

浅谈安科瑞智能照明系统在马来西亚国家石油公司项目的应用
摘要:随着社会经济的发展及网络技术、通信技术的提高,人们对照明设计提出了新的要求,它不仅要控制照明光源的发光时间、 亮度,而且与其它系统来配合不同的应用场合做出相应的灯光场景。本文介绍了马亚西亚石油公司智能照明项目的应…...
Java面对对象
Java面向对象 面对对象概述,类与对象,继承,重写与重载,多态,抽象,封装,包,泛型,异常 面对对象概述 什么是面向对象(OOP) 面向对象(Object Ori…...
代码随想录算法训练营|day24
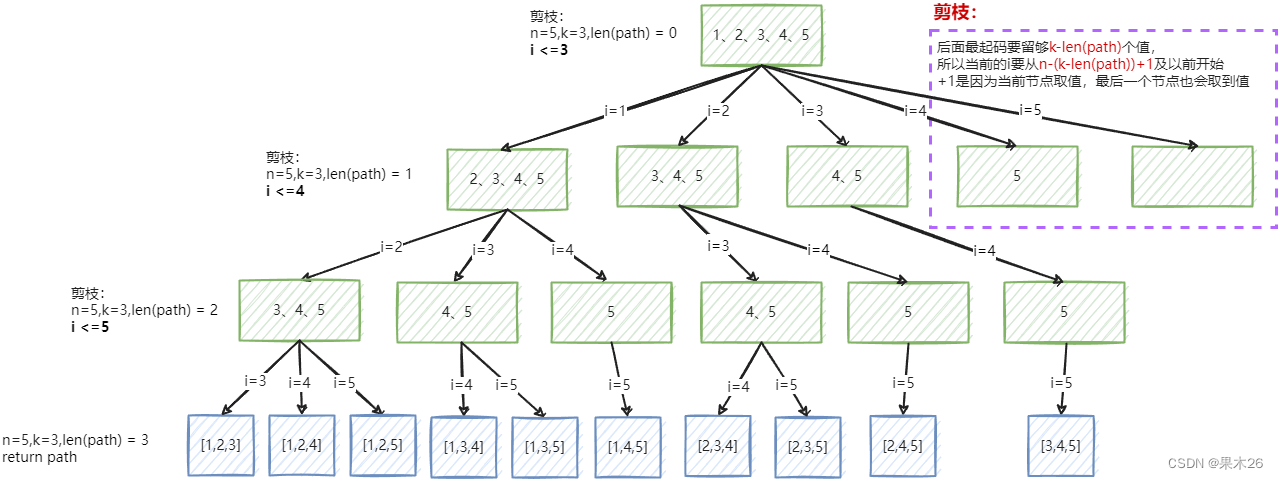
第七章 回溯算法 77.组合代码随想录文章详解总结 77.组合 以n5,k3为例 (1)for循环遍历,递归选择符合要求的值加入path,len(path)k时,返回 statrtIndex保证每次递归取到的值不重复 剪枝:i<n-(k-len(path))1 后续需要k-len(pat…...

嵌入式学习日记 16
共用体 union 共用体名 { 成员列表; //各个变量 }; //表示定义一个共用体类型 注意: 1.共用体 初始化 --- 只能给一个值,默认是给到第一个成员变量的 2.共用体成员变量辅助 共用体用的数据最终存储的 --- 应该是最后一次给到的值。 但是只能…...

JavaScript 中的 ES|QL:利用 Apache Arrow 工具
作者:来自 Elastic Jeffrey Rengifo 学习如何将 ES|QL 与 JavaScript 的 Apache Arrow 客户端工具一起使用。 想获得 Elastic 认证吗?了解下一期 Elasticsearch Engineer 培训的时间吧! Elasticsearch 拥有众多新功能,助你为自己…...

ESP32 I2S音频总线学习笔记(四): INMP441采集音频并实时播放
简介 前面两期文章我们介绍了I2S的读取和写入,一个是通过INMP441麦克风模块采集音频,一个是通过PCM5102A模块播放音频,那如果我们将两者结合起来,将麦克风采集到的音频通过PCM5102A播放,是不是就可以做一个扩音器了呢…...

大学生职业发展与就业创业指导教学评价
这里是引用 作为软工2203/2204班的学生,我们非常感谢您在《大学生职业发展与就业创业指导》课程中的悉心教导。这门课程对我们即将面临实习和就业的工科学生来说至关重要,而您认真负责的教学态度,让课程的每一部分都充满了实用价值。 尤其让我…...

华硕a豆14 Air香氛版,美学与科技的馨香融合
在快节奏的现代生活中,我们渴望一个能激发创想、愉悦感官的工作与生活伙伴,它不仅是冰冷的科技工具,更能触动我们内心深处的细腻情感。正是在这样的期许下,华硕a豆14 Air香氛版翩然而至,它以一种前所未有的方式&#x…...

LangChain知识库管理后端接口:数据库操作详解—— 构建本地知识库系统的基础《二》
这段 Python 代码是一个完整的 知识库数据库操作模块,用于对本地知识库系统中的知识库进行增删改查(CRUD)操作。它基于 SQLAlchemy ORM 框架 和一个自定义的装饰器 with_session 实现数据库会话管理。 📘 一、整体功能概述 该模块…...

【Redis】笔记|第8节|大厂高并发缓存架构实战与优化
缓存架构 代码结构 代码详情 功能点: 多级缓存,先查本地缓存,再查Redis,最后才查数据库热点数据重建逻辑使用分布式锁,二次查询更新缓存采用读写锁提升性能采用Redis的发布订阅机制通知所有实例更新本地缓存适用读多…...

【C++进阶篇】智能指针
C内存管理终极指南:智能指针从入门到源码剖析 一. 智能指针1.1 auto_ptr1.2 unique_ptr1.3 shared_ptr1.4 make_shared 二. 原理三. shared_ptr循环引用问题三. 线程安全问题四. 内存泄漏4.1 什么是内存泄漏4.2 危害4.3 避免内存泄漏 五. 最后 一. 智能指针 智能指…...

Python 实现 Web 静态服务器(HTTP 协议)
目录 一、在本地启动 HTTP 服务器1. Windows 下安装 node.js1)下载安装包2)配置环境变量3)安装镜像4)node.js 的常用命令 2. 安装 http-server 服务3. 使用 http-server 开启服务1)使用 http-server2)详解 …...
 error)
【前端异常】JavaScript错误处理:分析 Uncaught (in promise) error
在前端开发中,JavaScript 异常是不可避免的。随着现代前端应用越来越多地使用异步操作(如 Promise、async/await 等),开发者常常会遇到 Uncaught (in promise) error 错误。这个错误是由于未正确处理 Promise 的拒绝(r…...

Kubernetes 节点自动伸缩(Cluster Autoscaler)原理与实践
在 Kubernetes 集群中,如何在保障应用高可用的同时有效地管理资源,一直是运维人员和开发者关注的重点。随着微服务架构的普及,集群内各个服务的负载波动日趋明显,传统的手动扩缩容方式已无法满足实时性和弹性需求。 Cluster Auto…...
