【Java 数据结构】排序
排序算法
- 1. 排序的概念及引用
- 1.1 排序的概念
- 1.2 常见的排序算法
- 2. 常见排序算法的实现
- 2.1 插入排序
- 2.1.1 直接插入排序
- 2.1.2 希尔排序( 缩小增量排序 )
- 2.2 选择排序
- 2.2.1 直接选择排序
- 2.2.2 堆排序
- 2.3 交换排序
- 2.3.1冒泡排序
- 2.3.2 快速排序
- 2.3.3 快速排序非递归
- 2.4 归并排序
- 3. 排序算法复杂度及稳定性分析
1. 排序的概念及引用
1.1 排序的概念
排序:所谓排序,就是使一串记录,按照其中的某个或某些关键字的大小,递增或递减的排列起来的操作。
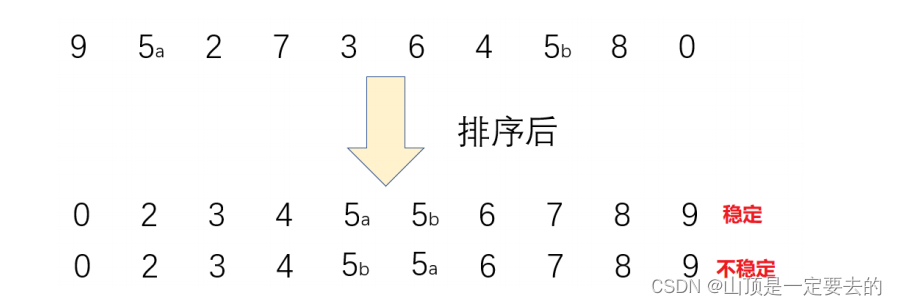
稳定性:假定在待排序的记录序列中,存在多个具有相同的关键字的记录,若经过排序,这些记录的相对次序保持不变,即在原序列中,r[i]=r[j],且r[i]在r[j]之前,而在排序后的序列中,r[i]仍在r[j]之前,则称这种排序算法是稳定的;否则称为不稳定的。
内部排序:数据元素全部放在内存中的排序
外部排序:数据元素太多不能同时放在内存中,根据排序过程的要求不能在内外存之间移动数据的排序。
1.2 常见的排序算法
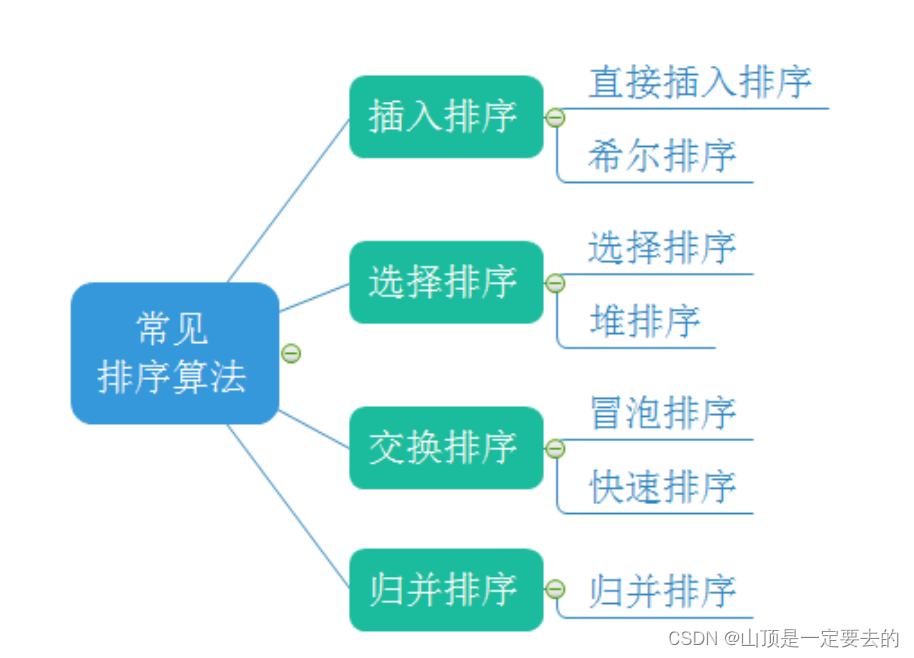
2. 常见排序算法的实现
2.1 插入排序
基本思想:
直接插入排序是一种简单的插入排序法,其基本思想是:
把待排序的记录按其关键码值的大小逐个插入到一个已经排好序的有序序列中,直到所有的记录插入完为止,得到一个新的有序序列 。实际中我们玩扑克牌时,就用了插入排序的思想。

2.1.1 直接插入排序
当插入第i(i>=1)个元素时,前面的array[0],array[1],…,array[i-1]已经排好序,此时用array[i]的排序码与array[i-
1],array[i-2],…的排序码顺序进行比较,找到插入位置即将array[i]插入,原来位置上的元素顺序后移
直接插入排序的特性总结:
1. 元素集合越接近有序,直接插入排序算法的时间效率越高
2. 时间复杂度:O(N^2)
3. 空间复杂度:O(1),它是一种稳定的排序算法
4. 稳定性:稳定
public static void insertSort(int[] array) {for (int i = 1; i < array.length; i++) {int tmp = array[i];int j = i-1;for (; j >= 0 ; j--) {//这里加不加等号 和稳定有关系// 但是:本身就是一个稳定的排序 可以实现为不稳定的排序// 但是 本身就是一个不稳定的排序 是不可能变成一个稳定的排序的if(array[j] > tmp) {array[j+1] = array[j];}else {//array[j+1] = tmp;break;}}array[j+1] = tmp;}}
2.1.2 希尔排序( 缩小增量排序 )
希尔排序法又称缩小增量法。希尔排序法的基本思想是:先选定一个整数,把待排序文件中所有记录分成多个组,所有距离为的记录分在同一组内,并对每一组内的记录进行排序。然后,取,重复上述分组和排序的工作。当到达=1时,所有记录在统一组内排好序。

希尔排序的特性总结:
- 希尔排序是对直接插入排序的优化。
- 当gap > 1时都是预排序,目的是让数组更接近于有序。当gap == 1时,数组已经接近有序的了,这样就会很
快。这样整体而言,可以达到优化的效果。我们实现后可以进行性能测试的对比。 - 希尔排序的时间复杂度不好计算,因为gap的取值方法很多,导致很难去计算,因此在好些书中给出的希尔排
序的时间复杂度都不固定: - 稳定性:不稳定
//希尔排序public static void shellSort(int[] array) {int gap = array.length;while (gap > 1) {gap /= 2;shell(array,gap);}}/*** 对每组进行插入排序* @param array* @param gap*/public static void shell(int[] array,int gap) {for (int i = gap; i < array.length; i++) {int tmp = array[i];int j = i-gap;for (; j >= 0 ; j-=gap) {//这里加不加等号 和稳定有关系// 但是:本身就是一个稳定的排序 可以实现为不稳定的排序// 但是 本身就是一个不稳定的排序 是不可能变成一个稳定的排序的if(array[j] > tmp) {array[j+gap] = array[j];}else {//array[j+1] = tmp;break;}}array[j+gap] = tmp;}}
2.2 选择排序
基本思想:
每一次从待排序的数据元素中选出最小(或最大)的一个元素,存放在序列的起始位置,直到全部待排序的数据元素排完 。
2.2.1 直接选择排序
- 在元素集合array[i]–array[n-1]中选择关键码最大(小)的数据元素
- 若它不是这组元素中的最后一个(第一个)元素,则将它与这组元素中的最后一个(第一个)元素交换
- 在剩余的array[i]–array[n-2](array[i+1]–array[n-1])集合中,重复上述步骤,直到集合剩余1个元素
【直接选择排序的特性总结】
- 直接选择排序思考非常好理解,但是效率不是很好。实际中很少使用
- 时间复杂度:O(N^2)
- 空间复杂度:O(1)
- 稳定性:不稳定
/*** 选择排序:* 时间复杂度:O(n^2)* 空间复杂度:O(1)* 稳定性:不稳定的排序* @param array*/public static void selectSort(int[] array) {for (int i = 0; i < array.length; i++) {int minIndex = i;for (int j = i+1; j < array.length; j++) {if(array[j] < array[minIndex]) {minIndex = j;}}swap(array,i,minIndex);}}
2.2.2 堆排序
堆排序(Heapsort)是指利用堆积树(堆)这种数据结构所设计的一种排序算法,它是选择排序的一种。它是通过堆
来进行选择数据。需要注意的是排升序要建大堆,排降序建小堆。
private static void createHeap(int[] array) {for (int parent = (array.length-1-1)/2; parent >= 0 ; parent--) {siftDown(array,parent,array.length);//alt+enter}}private static void siftDown(int[] array,int parent, int length) {int child = 2*parent + 1;while (child < length) {if(child+1 < length && array[child] < array[child+1]) {child++;}if(array[child] > array[parent]) {swap(array,child,parent);parent = child;child = 2*parent+1;}else {break;}}}/*** 时间复杂度:O(N*logN)* 空间复杂度:O(1)* 稳定性:不稳定的排序* @param array*/public static void heapSort(int[] array) {createHeap(array);int end = array.length-1;while (end > 0) {swap(array,0,end);siftDown(array,0,end);end--;}}2.3 交换排序
基本思想:所谓交换,就是根据序列中两个记录键值的比较结果来对换这两个记录在序列中的位置,交换排序的特点是:将键值较大的记录向序列的尾部移动,键值较小的记录向序列的前部移动。
2.3.1冒泡排序
【冒泡排序的特性总结】
- 冒泡排序是一种非常容易理解的排序
- 时间复杂度:O(N^2)
- 空间复杂度:O(1)
- 稳定性:稳定
/*** 时间复杂度:O(N^2)* 如果加了优化:最好情况下 可以达到O(n)* 空间复杂度:O(1)* 稳定性:稳定的排序** 优化:* 每一趟都需要判断 上一趟 有没有交换* @param array*/public static void bubbleSort(int[] array) {//i代表的是趟数for (int i = 0; i < array.length-1; i++) {boolean flg = false;//j来比较 每个数据的大小for (int j = 0; j < array.length-1-i; j++) {if(array[j] > array[j+1]) {swap(array,j,j+1);flg = true;}}if(!flg) {break;}}}
2.3.2 快速排序
快速排序是Hoare于1962年提出的一种二叉树结构的交换排序方法,其基本思想为:任取待排序元素序列中的某元素作为基准值,按照该排序码将待排序集合分割成两子序列,左子序列中所有元素均小于基准值,右子序列中所有元素均大于基准值,然后最左右子序列重复该过程,直到所有元素都排列在相应位置上为止
void QuickSort(int[] array, int left, int right){if(right - left <= 1)return;// 按照基准值对array数组的 [left, right)区间中的元素进行划分int div = partion(array, left, right);// 划分成功后以div为边界形成了左右两部分 [left, div) 和 [div+1, right)// 递归排[left, div)QuickSort(array, left, div-1);// 递归排[div+1, right)QuickSort(array, div+1, right);}
上述为快速排序递归实现的主框架,发现与二叉树前序遍历规则非常像,同学们在写递归框架时可想想二叉树前序遍历规则即可快速写出来,后序只需分析如何按照基准值来对区间中数据进行划分的方式即可。
将区间按照基准值划分为左右两半部分的常见方式有:
- Hoare版
private static int partition(int[] array, int left, int right) {int i = left;int j = right;int pivot = array[left];while (i < j) {while (i < j && array[j] >= pivot) {j--;}while (i < j && array[i] <= pivot) {i++;}swap(array, i, j);}swap(array, i, left);return i;
}
- 挖坑法
private static int partition(int[] array, int left, int right) {int i = left;int j = right;int pivot = array[left];while (i < j) {while (i < j && array[j] >= pivot) {j--;}array[i] = array[j];while (i < j && array[i] <= pivot) {i++;}array[j] = array[i];}array[i] = pivot;return i;}
- 前后指针
private static int partition(int[] array, int left, int right) {int prev = left ;int cur = left+1;while (cur <= right) {if(array[cur] < array[left] && array[++prev] != array[cur]) {swap(array,cur,prev);}cur++;}swap(array,prev,left);return prev;}
2.3.3 快速排序非递归
void quickSortNonR(int[] a, int left, int right) {Stack<Integer> st = new Stack<>();st.push(left);st.push(right);while (!st.empty()) {right = st.pop();left = st.pop();if(right - left <= 1)continue;int div = PartSort1(a, left, right);// 以基准值为分割点,形成左右两部分:[left, div) 和 [div+1, right)st.push(div+1);st.push(right);st.push(left);st.push(div);}}
快速排序总结
- 快速排序整体的综合性能和使用场景都是比较好的,所以才敢叫快速排序
- 时间复杂度:O(N*logN)
- 空间复杂度:O(logN)
- 稳定性:不稳定
2.4 归并排序
基本思想
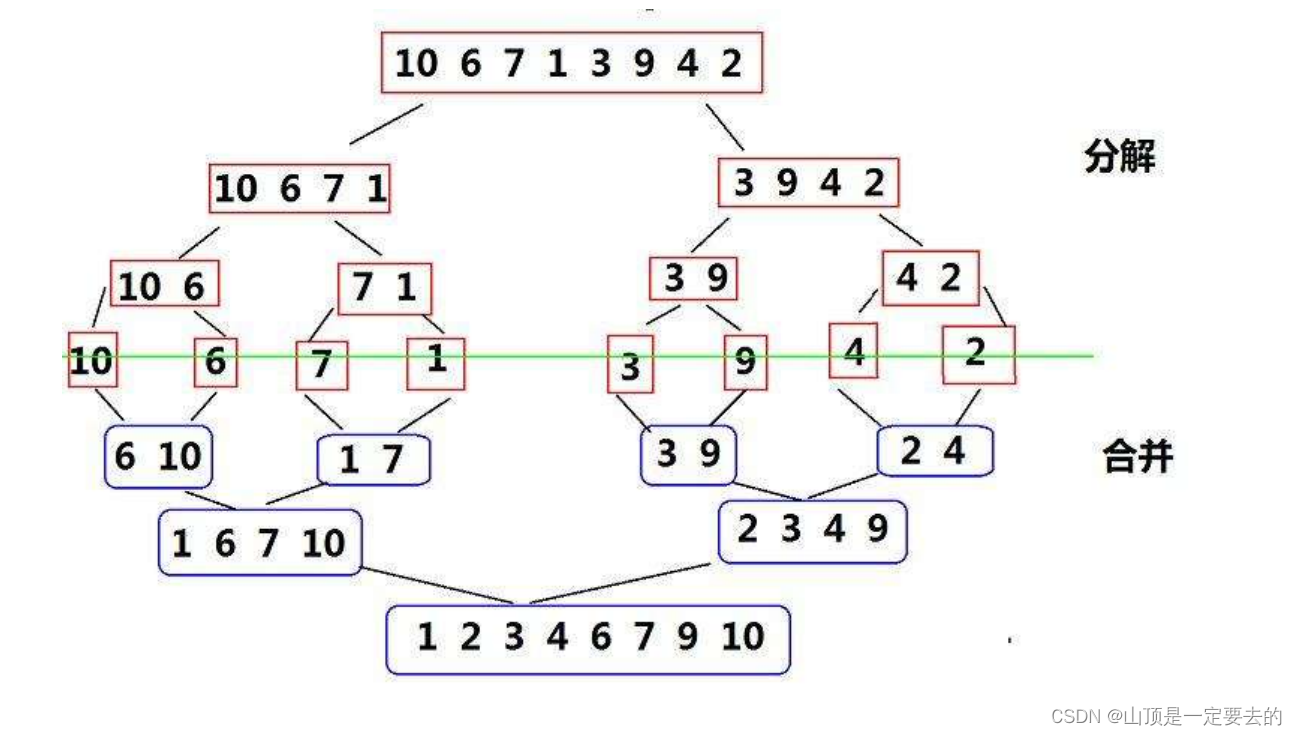
归并排序(MERGE-SORT)是建立在归并操作上的一种有效的排序算法,该算法是采用分治法(Divide and
Conquer)的一个非常典型的应用。将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段间有序。若将两个有序表合并成一个有序表,称为二路归并。 归并排序核心步骤:
/*** 时间复杂度:O(N*logN)* 空间复杂度:O(logN)* 稳定性:稳定的排序* 目前为止3个稳定的排序:直接插入排序、冒泡排序、归并排序* @param array*/public static void mergeSort(int[] array) {mergeSortFun(array,0,array.length-1);}private static void mergeSortFun(int[] array,int start,int end) {if(start >= end) {return;}int mid = (start+end)/2;mergeSortFun(array,start,mid);mergeSortFun(array,mid+1,end);//合并merge(array,start,mid,end);}private static void merge(int[] array, int left, int mid, int right) {int s1 = left;//可以不定义,这样写为了好理解int e1 = mid;//可以不定义,这样写为了好理解int s2 = mid+1;int e2 = right;//可以不定义,这样写为了好理解//定义一个新的数组int[] tmpArr = new int[right-left+1];int k = 0;//tmpArr数组的下标//同时满足 证明两个归并段 都有数据while (s1 <= e1 && s2 <= e2) {if(array[s1] <= array[s2]) {tmpArr[k++] = array[s1++];}else {tmpArr[k++] = array[s2++];}}while (s1 <= e1) {tmpArr[k++] = array[s1++];}while (s2 <= e2) {tmpArr[k++] = array[s2++];}//把排好序的数据 拷贝回原来的数组array当中for (int i = 0; i < tmpArr.length; i++) {array[i+left] = tmpArr[i];}}归并排序总结
- 归并的缺点在于需要O(N)的空间复杂度,归并排序的思考更多的是解决在磁盘中的外排序问题。
- 时间复杂度:O(N*logN)
- 空间复杂度:O(N)
- 稳定性:稳定
【 海量数据的排序问题】
外部排序:排序过程需要在磁盘等外部存储进行的排序
前提:内存只有 1G,需要排序的数据有 100G
因为内存中因为无法把所有数据全部放下,所以需要外部排序,而归并排序是最常用的外部排序
- 先把文件切分成 200 份,每个 512 M
- 分别对 512 M 排序,因为内存已经可以放的下,所以任意排序方式都可以
- 进行 2路归并,同时对 200 份有序文件做归并过程,最终结果就有序了
3. 排序算法复杂度及稳定性分析

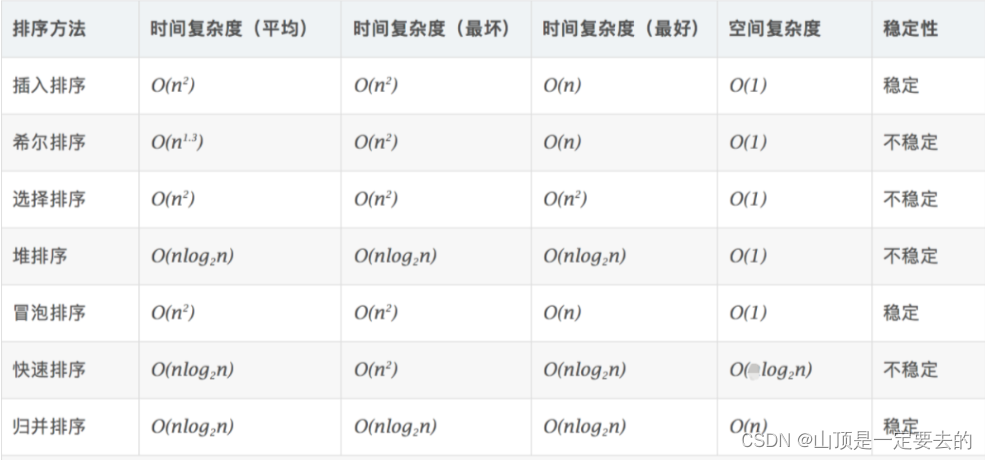
相关文章:

【Java 数据结构】排序
排序算法 1. 排序的概念及引用1.1 排序的概念1.2 常见的排序算法 2. 常见排序算法的实现2.1 插入排序2.1.1 直接插入排序2.1.2 希尔排序( 缩小增量排序 ) 2.2 选择排序2.2.1 直接选择排序2.2.2 堆排序 2.3 交换排序2.3.1冒泡排序2.3.2 快速排序2.3.3 快速排序非递归 2.4 归并排…...
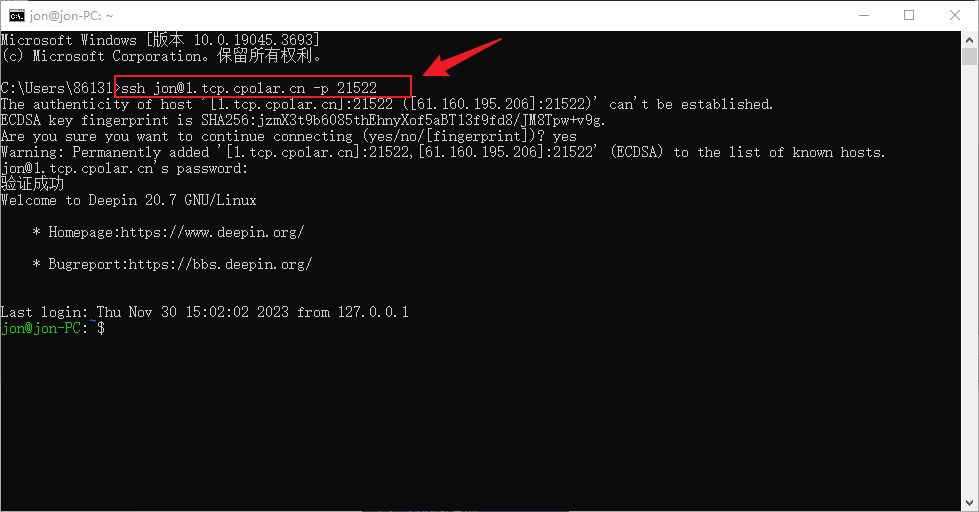
Deepin如何开启与配置SSH实现无公网ip远程连接
文章目录 前言1. 开启SSH服务2. Deppin安装Cpolar3. 配置ssh公网地址4. 公网远程SSH连接5. 固定连接SSH公网地址6. SSH固定地址连接测试 前言 Deepin操作系统是一个基于Debian的Linux操作系统,专注于使用者对日常办公、学习、生活和娱乐的操作体验的极致࿰…...
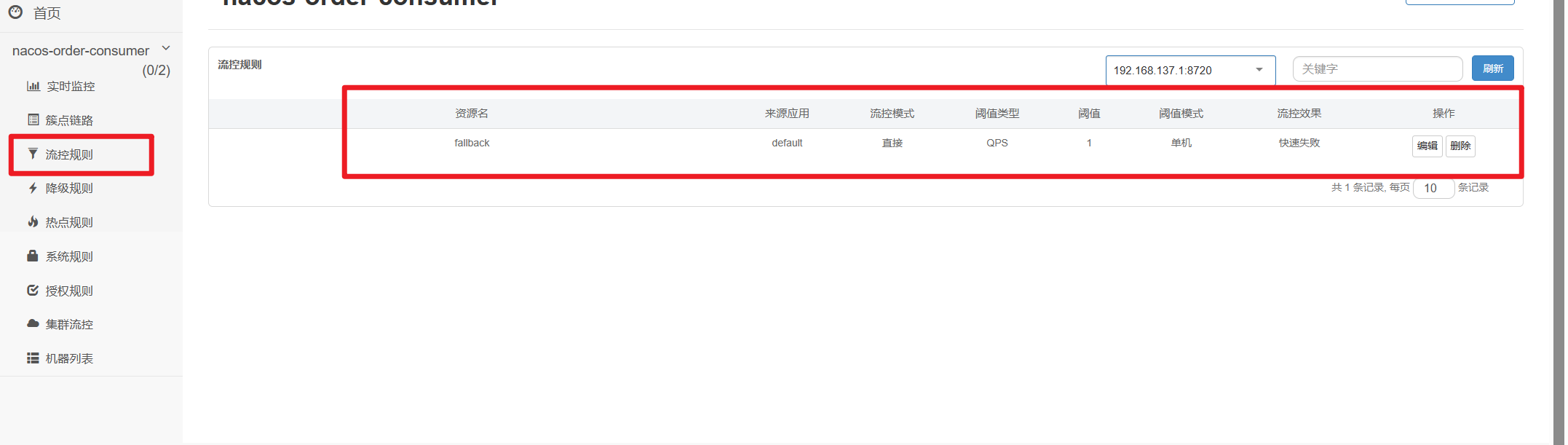
【Springcloud篇】学习笔记十(十七章):Sentinel实现熔断与限流——Hystrix升级
第十七章_Sentinel实现熔断与限流 1.Sentinel介绍 1.1是什么 随着微服务的流行,服务和服务之间的稳定性变得越来越重要。 Sentinel 以流量为切入点,从流量控制、熔断降级、系统负载保护等多个维度保护服务的稳定性。 用来代替Hystrix Sentinel 具有…...
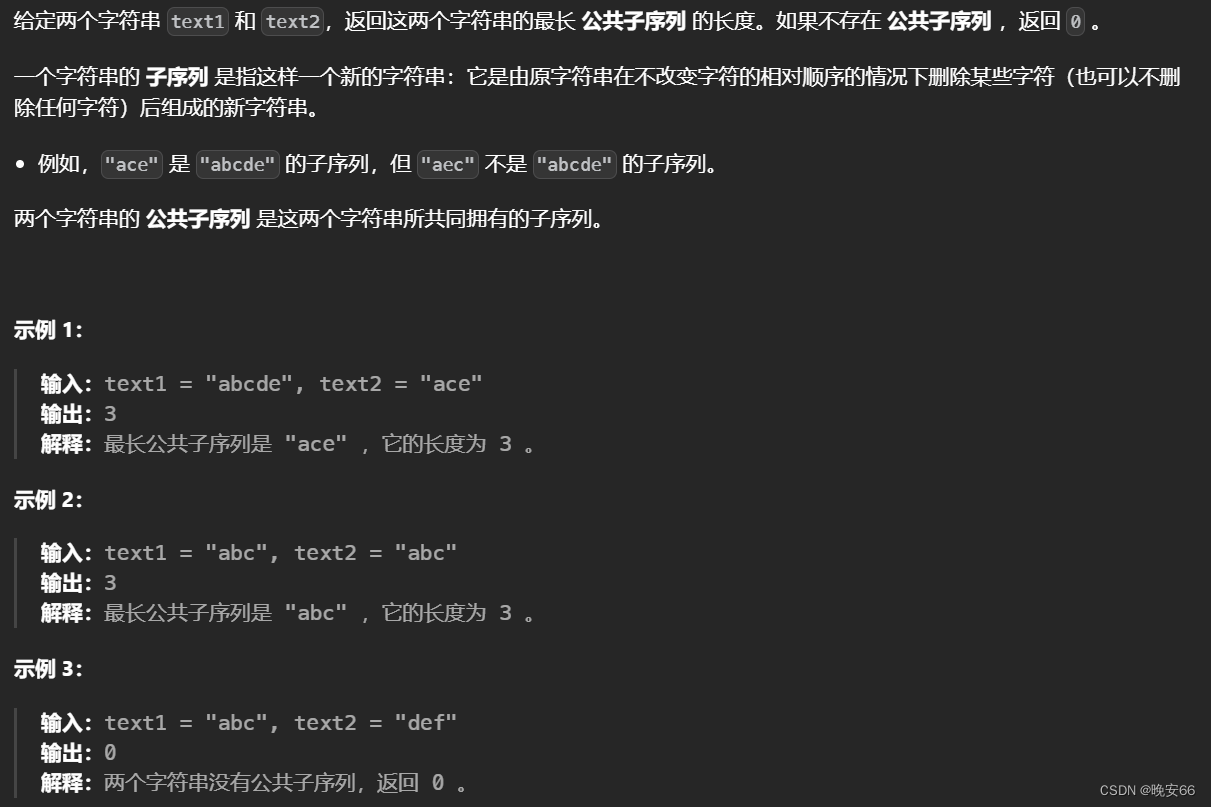
【算法与数据结构】718、1143、LeetCode最长重复子数组 最长公共子序列
文章目录 一、718、最长重复子数组二、1143、最长公共子序列三、完整代码 所有的LeetCode题解索引,可以看这篇文章——【算法和数据结构】LeetCode题解。 一、718、最长重复子数组 思路分析: 第一步,动态数组的含义。 d p [ i ] [ j ] dp[i]…...
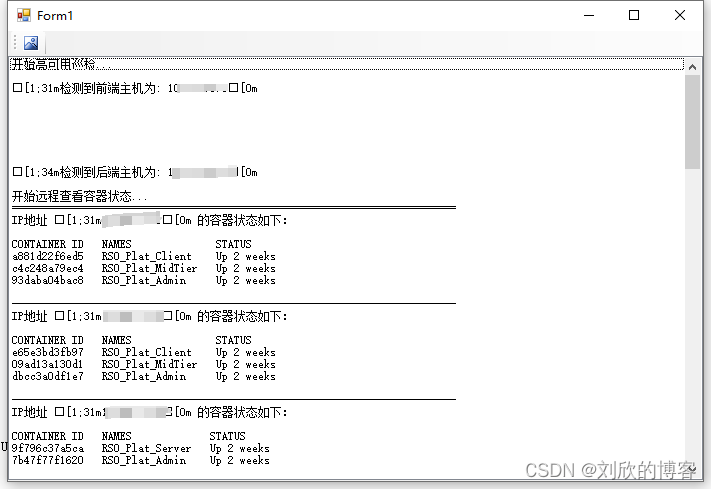
C# SSH.NET 长命令及时返回
在SSH中执行长时间的命令,SSH.NET及时在文本框中返回连续显示结果。 c# - Execute long time command in SSH.NET and display the results continuously in TextBox - Stack Overflow 博主管理了一个服务器集群,准备上自动巡检工具,测试在…...

Rust学习之Features
Rust学习之Features 一 什么是 Features二 默认 feature三 简单的features应用示例四 可选(optional)的依赖五 依赖的特性5.1 在依赖表中指定5.2 在features表中指定 六 命令行中特性控制七 特性统一路径八 其它8.1 相互排斥特性8.2 观察启用特性8.3 Feature resolver version …...

云计算基础(云计算概述)
目录 一、云计算概述 1.1 云计算的概念 1.1.1 云计算解决的问题 1.1.2 云计算的概念 1.1.3 云计算的组成 1.2 云计算主要特征 1.2.1 按需自助服务 1.2.2 泛在接入 1.2.3 资源池化 1.2.4 快速伸缩性 1.2.5 服务可度量 1.3 云计算服务模式 1.3.1 软件即服务(Softwar…...
【机器学习】科学库使用手册第2篇:机器学习任务和工作流程(已分享,附代码)
本系列文章md笔记(已分享)主要讨论人工智能相关知识。主要内容包括,了解机器学习定义以及应用场景,掌握机器学习基础环境的安装和使用,掌握利用常用的科学计算库对数据进行展示、分析,学会使用jupyter note…...

【React】前端项目引入阿里图标
【React】前端项目引入阿里图标 方式11、登录自己的iconfont-阿里巴巴矢量图标库,把需要的图标加入到自己的项目中去;2、加入并进入到项目中去选择Font class 并下载到本地3、得到的文件夹如下4. 把红框中的部分粘贴到自己的项目中(public 文…...
Javascript入门:第三个知识点:javascript里的数据类型、运算符
数字类型 123 //整数 123.1 //浮点数 1.123e3 //科学计数法 -10 //负数 NaN //not a number Infinity //无限大 以上的类型在javascript里都是数字类型 字符串类型 在开始之前,我需要先说明白两个知识点: console.log()是啥? let 与 v…...
最新版国产会声会影2024新功能爆料
会声会影2024是一个视频编辑软件,具备以下功能: 会声会影2024安装包下载如下: https://wm.makeding.com/iclk/?zoneid55677 1. 视频剪辑:可以对视频进行剪辑、裁剪、拼接和分割操作,实现对视频片段的精确控制。 2. 音频编辑&…...

Pandas处理Excel文件的实用指南 - Python开发技巧XI
处理Excel文件是数据分析师日常工作中的常见任务之一。 幸运的是,Python的Pandas库提供了一套强大的工具,使得读取、处理和写入Excel文件变得既清晰又快捷。 在本篇博客中,我们将探讨如何使用Pandas的 read_excel 方法来读取Excel文件&#x…...
泰克示波器(TBS2000系列)触发功能使用讲解——边沿触发
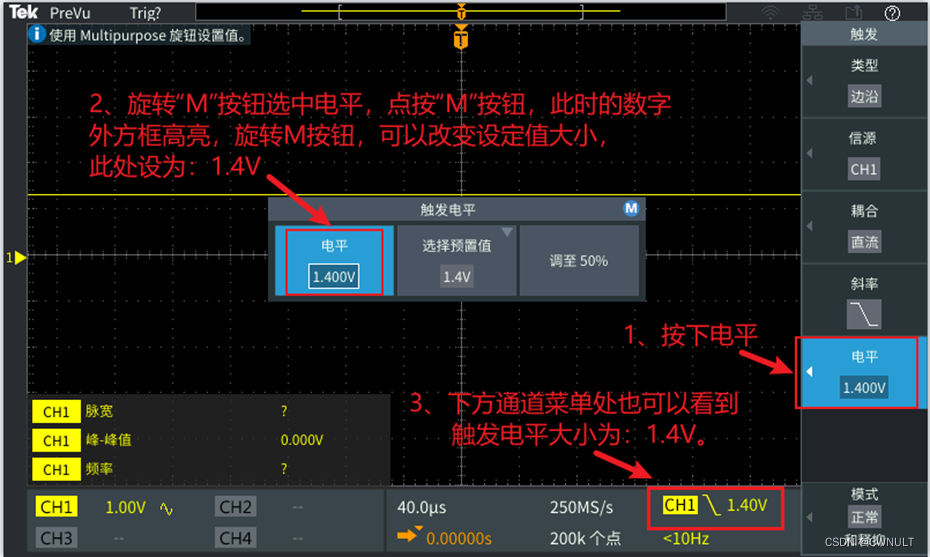
# Trigger区域 触发区域用于对触发功能进行配置。示波器的触发功能用于采集(Acquire)那些在瞬间出现的信号,便于我们分析观察,此时可以当做逻辑分析仪使用。触发区域按钮包括:menu、Level\Force Trig三个。 目录 1.1 …...

C++学习Day01之C++对C语言增强和扩展
目录 一、程序及输出1.1 全局变量检测增强1.2 函数检测增强1.3 类型转换检测增强1.4 struct增强1.5 bool类型扩展1.6 三目运算符增强1.7 const增强1.7.1 全局Const对比1.7.2 局部Const对比1.7.3 Const变量初始化数组1.7.3 Const修饰变量的链接性 二、分析总结 一、程序及输出 …...
【文件上传WAF绕过】<?绕过、.htaccess木马、.php绕过
🍬 博主介绍👨🎓 博主介绍:大家好,我是 hacker-routing ,很高兴认识大家~ ✨主攻领域:【渗透领域】【应急响应】 【python】 【VulnHub靶场复现】【面试分析】 🎉点赞➕评论➕收藏…...

flutter如何实现省市区选择器
前言 当我们需要用户填写地址时,稳妥的做法是让用户通过“滚轮”来滑动选择省份,市,区,此文采用flutter的第三方库来实现这一功能,比调用高德地图api简单一些。 流程 选择库 这里我选择了一个最近更新且支持中国的…...

Python——将Pyaudio的frame音频数据转换成wave格式
要将pyaudio捕获的音频帧(frame)数据转换成wave模块可以直接处理的格式,通常意味着你需要将这些音频帧数据组装成一个完整的音频流,并确保它们以wave模块期望的格式进行存储。但是,如果你的目的是将这些帧数据直接转换…...

Vue 上门取件时间组件
本文使用vue2.0elementui 制作一个上门取件时间组件,类似顺丰,样式如下: 大概功能:点击期望上门时间,下面出现一个弹框可以选择时间: 首先我们定义一些需要的数据: data() {return {isDropdown…...

学习python第一天
1.输出 print("Hello, World!") 2.退出命令提升符 exit() 3.Python 缩进 实例 if 5 > 2:print("Five is greater than two!") 空格数取决于程序员,但至少需要一个。 您必须在同一代码块中使用相同数量的空格,否则 Python 会…...

interface转string输出打印
文章目录 前言一、interface 转json再转string二、使用类型判断 前言 在开发过程中,有时我们使用interface类型接受某些参数接口或返回类型,但输出时,比如记录日志时存在很多不方便情况,输出string发现输出的乱七八糟,…...

vscode里如何用git
打开vs终端执行如下: 1 初始化 Git 仓库(如果尚未初始化) git init 2 添加文件到 Git 仓库 git add . 3 使用 git commit 命令来提交你的更改。确保在提交时加上一个有用的消息。 git commit -m "备注信息" 4 …...

中南大学无人机智能体的全面评估!BEDI:用于评估无人机上具身智能体的综合性基准测试
作者:Mingning Guo, Mengwei Wu, Jiarun He, Shaoxian Li, Haifeng Li, Chao Tao单位:中南大学地球科学与信息物理学院论文标题:BEDI: A Comprehensive Benchmark for Evaluating Embodied Agents on UAVs论文链接:https://arxiv.…...

基于Flask实现的医疗保险欺诈识别监测模型
基于Flask实现的医疗保险欺诈识别监测模型 项目截图 项目简介 社会医疗保险是国家通过立法形式强制实施,由雇主和个人按一定比例缴纳保险费,建立社会医疗保险基金,支付雇员医疗费用的一种医疗保险制度, 它是促进社会文明和进步的…...

DAY 47
三、通道注意力 3.1 通道注意力的定义 # 新增:通道注意力模块(SE模块) class ChannelAttention(nn.Module):"""通道注意力模块(Squeeze-and-Excitation)"""def __init__(self, in_channels, reduction_rat…...

HTML 列表、表格、表单
1 列表标签 作用:布局内容排列整齐的区域 列表分类:无序列表、有序列表、定义列表。 例如: 1.1 无序列表 标签:ul 嵌套 li,ul是无序列表,li是列表条目。 注意事项: ul 标签里面只能包裹 li…...

#Uniapp篇:chrome调试unapp适配
chrome调试设备----使用Android模拟机开发调试移动端页面 Chrome://inspect/#devices MuMu模拟器Edge浏览器:Android原生APP嵌入的H5页面元素定位 chrome://inspect/#devices uniapp单位适配 根路径下 postcss.config.js 需要装这些插件 “postcss”: “^8.5.…...
多光源(Multiple Lights))
C++.OpenGL (14/64)多光源(Multiple Lights)
多光源(Multiple Lights) 多光源渲染技术概览 #mermaid-svg-3L5e5gGn76TNh7Lq {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-3L5e5gGn76TNh7Lq .error-icon{fill:#552222;}#mermaid-svg-3L5e5gGn76TNh7Lq .erro…...
:观察者模式)
JS设计模式(4):观察者模式
JS设计模式(4):观察者模式 一、引入 在开发中,我们经常会遇到这样的场景:一个对象的状态变化需要自动通知其他对象,比如: 电商平台中,商品库存变化时需要通知所有订阅该商品的用户;新闻网站中࿰…...

安全突围:重塑内生安全体系:齐向东在2025年BCS大会的演讲
文章目录 前言第一部分:体系力量是突围之钥第一重困境是体系思想落地不畅。第二重困境是大小体系融合瓶颈。第三重困境是“小体系”运营梗阻。 第二部分:体系矛盾是突围之障一是数据孤岛的障碍。二是投入不足的障碍。三是新旧兼容难的障碍。 第三部分&am…...

自然语言处理——文本分类
文本分类 传统机器学习方法文本表示向量空间模型 特征选择文档频率互信息信息增益(IG) 分类器设计贝叶斯理论:线性判别函数 文本分类性能评估P-R曲线ROC曲线 将文本文档或句子分类为预定义的类或类别, 有单标签多类别文本分类和多…...
