【初中生讲机器学习】4. 支持向量机算法怎么用?一个实例带你看懂!
创建时间:2024-02-02
最后编辑时间:2024-02-03
作者:Geeker_LStar
你好呀~这里是 Geeker_LStar 的人工智能学习专栏,很高兴遇见你~
我是 Geeker_LStar,一名初三学生,热爱计算机和数学,我们一起加油~!
⭐(●’◡’●) ⭐
那就让我们开始吧!
上一篇【初中生讲机器学习】3. 支持向量机(SVM)一万字详解!超全超详细超易懂!当中,我们已经详细了解了支持向量机算法以及它背后的数学原理,但是上一篇文章中没有给出实例代码,so 这一篇主要就通过一个实例来看看支持向量机算法应该怎么实现,有哪些要点~
完整代码见文末~
实例:利用支持向量机对鸢尾花进行分类。
(神奇,我这学期的作文里貌似三次写到鸢尾花诶)
话不多说,首先,我们导入各种需要的库(or 需要的函数方法 or 数据集)。
'''第一步,导入各种需要的库'''
import matplotlib.pyplot as plt # 用于数据可视化
import matplotlib as mpl
from sklearn import svm # 引入封装好的 SVM 算法
from sklearn.datasets import load_iris # 引入鸢尾花数据集,共 150 组数据
from sklearn.model_selection import train_test_split # 划分训练集和测试集的函数方法
from sklearn.metrics import accuracy_score # 评判测试准确度的函数方法
import numpy as np # 进行科学计算
matplotlib,进行数据可视化的库。
numpy 用于进行科学计算。
scikit learn,即 sklearn 库,是机器学习中非常重要的一个库,它封装了大量常用算法,如分类、回归、降维、聚类等,并且提供一些常用数据集,其中就包括本例中用到的鸢尾花数据集。
接着,我们需要对鸢尾花数据集有一个了解,先加载它,然后输出一些它的特征。
iris = load_iris() # 加载数据集
print(iris.target) # 数据标签(分类结果标签)
print(iris.target_names) # 三种鸢尾花的名字
print(iris.feature_names) # 四个分类特征的名字
这是输出结果,可以看到,数据集中的鸢尾花一共有三类 150 个,每一类有 50 个。分类标准是【萼片长度】【萼片宽度】【花瓣长度】【花瓣宽度】。
[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 00 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 11 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2 22 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 22 2]
['setosa' 'versicolor' 'virginica']
['sepal length (cm)', 'sepal width (cm)', 'petal length (cm)', 'petal width (cm)']
再来看一下每一个鸢尾花数据是怎么表示的(没错其实就是四维向量,因为四个特征嘛),以及它们对应的数据标签。
X = iris.data # 输入数据(150 个四维向量),样本特征,[n_samples * n_features] 的二维数组
print(X.shape, X) # X.shape,输出 X 数组的行数和列数
y = iris.target # 数据标签 or 分类结果(共三种每种 50 个数据)
print(y.shape, y)
输出如下(一部分),大意是:输入数据一共 150 个,每个都是一个四维向量,对应的数据标签是 0 或 1 或 2。
(150, 4) [[5.1 3.5 1.4 0.2][4.9 3. 1.4 0.2][4.7 3.2 1.3 0.2][4.6 3.1 1.5 0.2](150,) [0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 00 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 11 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2 22 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 22 2]
哦?这样不够直观?看不出这 150 组数据在分布上有什么特点?没事,咱有 matplotlib,画个图嘛!
errr,我们分别以前两个特征(萼片长宽)和后两个特征(花瓣长宽)为特征画图。画完图其实可以看出一些东西,不过这里先不透露。
# 以前两个特征(花萼长度、花萼宽度)绘图
X = iris.data[:, :2] # 切片操作,选取前两个特征
plt.scatter(X[y == 0, 0], X[y == 0, 1], color = "red", marker = "o")
plt.scatter(X[y == 1, 0], X[y == 1, 1], color = "green", marker = "+")
plt.scatter(X[y == 2, 0], X[y == 2, 1], color = "blue", marker = "x")
plt.xlabel('sepal length', fontsize=20)
plt.ylabel('sepal width', fontsize=20)
plt.title('Iris names', fontsize=30)
plt.show()
这是这些鸢尾花的萼片长宽的分布图,不难发现,通过萼片长宽可以比较好的将第一种鸢尾花(红色)和第二三种(绿/蓝色)区分开,但是第二种和第三种之间却不太好区分。
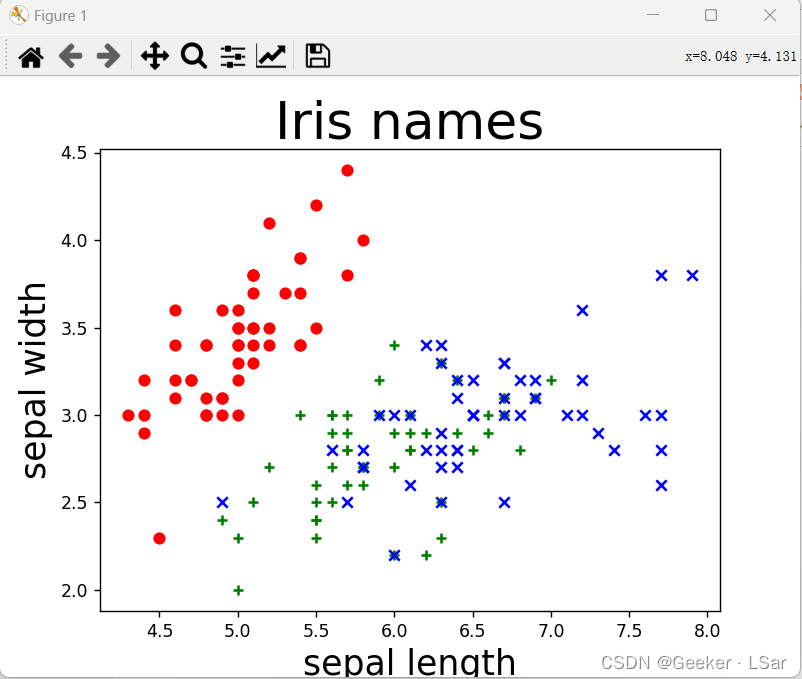
再来看看花瓣长宽的情况。
# 以后两个特征(花瓣长度、花瓣宽度)绘图(发现后两个特征能够更好地区分三类鸢尾花)
X = iris.data[:, 2:]
plt.scatter(X[y == 0, 0], X[y == 0, 1], color = "red", marker = "o")
plt.scatter(X[y == 1, 0], X[y == 1, 1], color = "green", marker = "+")
plt.scatter(X[y == 2, 0], X[y == 2, 1], color = "blue", marker = "x")
plt.xlabel('petal length', fontsize=20)
plt.ylabel('petal width', fontsize=20)
plt.title('Iris names', fontsize=30)
plt.show()
分布图长这样,不难看出,可以通过花瓣长宽特征将三种鸢尾花大致分开,【只按照花瓣特征分】比【只按照萼片特征分】的效果更好(为什么提到这个,因为后面要写相关代码~)。
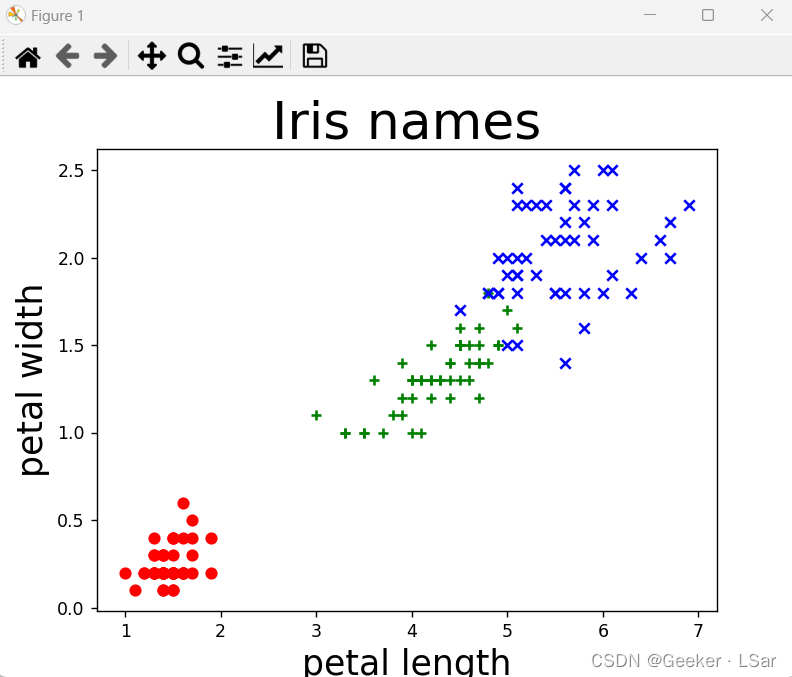
ok,现在我们对整个数据集已经有了大致的了解,可以利用支持向量机来分类啦!
通常来讲,用 SVM 分类可以按照这个顺序进行,其中 2、3 可以反过来:
- 获取所需数据集(全部特征 or 某个或某几个特征(切片))
- 定义支持向量机(svm.SVC())
- 划分训练集和测试集(train_test_split())
- 利用训练集进行训练(fit())
- 测试,预测测试集的输出结果(predict())
- 计算测试准确率并输出,模型评价(accuracy_score())
- 绘制结果(如果需要)
那我们就按照这个步骤来吧!先来最简单的,用全部特征进行分类,先训练再测试。
第一步,获取所需数据集,这两行代码的意思上面已经解释过:
X = iris.data
y = iris.target
第二步,定义支持向量机,解释一下其中的一些参数,这些参数的详细讲解都在上一篇:
- kernel:核函数类型,“linear” 表示线性核函数,“poly” 表示多项式核函数,“rbf” 表示高斯核函数(径向基函数)。
- C:惩罚项,默认值为 1。C 的值很关键,过小会导致模型的泛化能力弱(过拟合),过大又会导致欠拟合。
- gamma:核函数的核系数,一般情况下默认为 1/n_features。
- probability:是否支持输出样本属于不同类的概率,True 表示支持。
svm1 = svm.SVC(kernel="rbf", C=1, gamma="auto", probability=True)
第三步,划分训练集和测试集:
train_test_split() 用于划分训练集和测试集,其中,test_size 指测试集数据量占数据总量的百分比,0.3 即有 30% 的数据用于测试,其余数据用于训练;random_state 是随机数种子,改变它可以获得不同的数据划分,通常在交叉验证中使用。
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=218)
第四步,利用训练集进行训练:
fit() 方法,用于训练支持向量机,也就是拟合。
svm2.fit(X_train, y_train)
第五步,测试,预测测试集的输出结果:
训练完 SVM,就让它去预测一下测试集的数据吧。
predict() 函数用于预测。
y_predict = svm2.predict(X_test)
第六步,计算测试准确率并输出,也就是模型评价:
accuracy_score() 函数计算模型预测的准确率,是评价模型性能的一项参考指标,与之类似的参考指标还有召回率、ROC 曲线、AUC 值等,这些在第二篇中讲过~(sklearn 库也提供其他参考指标的函数方法,但是本例中用不到)。
print("准确率:", accuracy_score(y_test, y_predict))
ok!此时一个 SVM 的训练+测试就完成了!我这里的准确率是 95.6%。
如果对准确率不满意,可以尝试调整惩罚系数 C,也可以尝试换一种核函数,或者提高训练集的占比使模型得到更充分的训练,等等。
ok,走了一遍基础流程,其实 SVM 的训练并不难的()下面我们来看看如果我们想按照某些特征进行分类(比如之前提到的按照萼片长宽分类),并且想更直观地看到这个超平面是怎么划分的,我们应该怎么做。
其实大体上没什么变化,只不过在获取数据的时候需要做一个切片处理,语法和 Python 当中的列表切片是一样的。
X2 = iris.data[:, :2] # :2 表示取前两个特征,即萼片长和萼片宽
别的代码和上面完全一样,为了和上面进行区分,把 svm 和 X 的角标改了一下:
X2 = iris.data[:, :2] # :2 表示取前两个特征,即萼片长和萼片宽
svm3 = svm.SVC(kernel="rbf", C=3, gamma="auto")
X2_train, X2_test, y2_train, y2_test = train_test_split(X2, y, test_size=0.3, random_state=218)
svm3.fit(X2_train, y2_train)
y2_predict = svm3.predict(X2_test)
print("准确率:", accuracy_score(y2_test, y2_predict))
draw1(svm3, X2) # 绘图
你可能发现了,这段代码里定义了一个用于绘图的 draw 函数,这个函数蛮关键的,我们拆解着来写。
first,明确需求,我们希望通过前两个特征(萼片长宽)进行分类,并将结果可视化,也就是要画出决策超平面,直观地看出萼片长宽在哪一部分的花会被分到哪一类。
先把最终结果放在这,这样后面拆解每一步就会变得好理解~
下图中,背景色块相交的地方就是决策超平面(其实就是一条线),不同的色块代表花萼长宽在不同范围的鸢尾花会被分到不同的类(一个色块就是一类)。
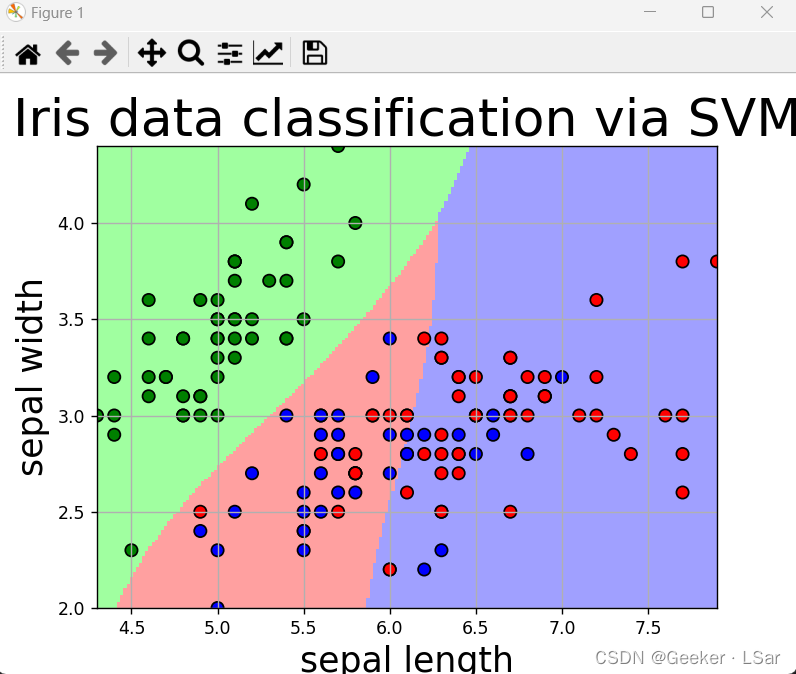
其实这块主要是数据处理 and 可视化,并且这种可视化套路其实是通用的,后面的文章中会讲 KNN(K 最近邻)算法,它的实例也可以用这一套可视化流程。
首先,花萼长宽的分布都在一定范围内,我们可以用它们的最小值和最大值作为 xy 轴的起止点,如下。
# 获取坐标值的范围
x1_min, x1_max = X[:, 0].min(), X[:, 0].max()
x2_min, x2_max = X[:, 1].min(), X[:, 1].max()
# 坐标轴范围
plt.xlim(x1_min, x1_max)
plt.ylim(x2_min, x2_max)
接着,问题来了,怎么找到决策线?上图中那些表示分类的背景色块是怎么画出来的?
这个思路很好:色块其实就是一个个点密集分布组成的,我们可以在坐标系中取很多很多点(为了保证精确度,这些点之间的间隔应该相等且足够小),用已经训练好的模型预测这些点会被分到哪一类。对于分到不同类的点,用不同的颜色在坐标系中画出它们。这样这些密集的点就会形成一个“色块”,不同颜色的色块也就代表了不同的类。
(对之所以高亮这一部分就是我觉得这个思路真的太棒了!)
来写写。
first,我们要取一堆间隔足够小的点,比如在横纵坐标最小值和最大值之间都均等取 200 个值,这样一共就选取了 200*200 = 40000 个点,这么多点足以让坐标系看起来被填满了。
# 生成坐标系中的网格点(2D)
# 200j,复数,即在这个范围中取 200 个点
x1, x2 = np.mgrid[x1_min:x1_max:200j, x2_min:x2_max:200j]
second,目前的 x1、x2 都还只是单独的横坐标和单独的纵坐标,用 stack() 函数把它们重新组合一下,新的数组是 40000 个点的坐标。
# 构造测试点(坐标点)并输出其坐标
# stack() 方法,将两个二维数组合并成一个新的二维数组
grid_test = np.stack((x1.flat, x2.flat), axis=1)
print('坐标点的坐标数据:\n', grid_test)
输出是这样的,可以看到和图中的坐标范围是一致的。
坐标点的坐标数据:[[1. 0.1 ][1. 0.1120603][1. 0.1241206]...[6.9 2.4758794][6.9 2.4879397][6.9 2.5 ]]
上一篇中提到了函数间隔,它反映点到决策超平面的距离,函数间隔大于等于 1 说明分类正确,越大说明越可能是这一类。
这里获得输出构造的坐标点的函数间隔(可以看出它们应该分到哪一类),用 decision_function() 函数,然后输出坐标点预测结果。
and then 输出一下原始数据集中的数据被分到每一类的概率,用 predict_proba() 函数。
其实这些可以不用输出,但是为了更详细地知道每个函数都干了什么,我把输出结果放在代码后面了。
# decision_function 多分类情况
# 输出样本到决策超平面的距离(函数间隔),反映属于每个分类的可能性
# 第 n 个数是属于第 n 类的可能性
# 数越大,说明越有可能属于这个分类
z = svm.decision_function(grid_test)
print('坐标点到超平面的距离(函数间隔):\n', z)
# 预测并输出分类结果,得到 [0, 0, ..., 2, 2]
grid_hat = svm.predict(grid_test)
print('坐标点预测结果:\n', grid_hat)
# 预测并输出测试集中的数据属于每个类别的概率
probably = svm.predict_proba(X)
print('测试数据的预测概率:\n', probably)
输出结果:
坐标点到超平面的距离(函数间隔):[[ 2.21808359 -0.18477028 0.86886414][ 2.21824232 -0.18491925 0.86865134][ 2.21838742 -0.18505706 0.86845955]...[-0.18169166 0.85623648 2.22058861][-0.18145152 0.85663691 2.22031407][-0.18120477 0.85704722 2.22003204]]坐标点预测结果:[0 0 0 ... 2 2 2]
测试数据的预测概率:[[0.95790549 0.0183466 0.02374791][0.95790549 0.0183466 0.02374791][0.95498744 0.01979717 0.02521539][0.95897025 0.01779033 0.02323941](这里省略了后面的)
重要的逻辑都说完了,剩下就是画图的事情了,画图部分的代码的功能注释里都写了~
# 使得 grid_hat 和 x1 的数组形式一致
grid_hat = grid_hat.reshape(x1.shape)
cm_light = mpl.colors.ListedColormap(['#A0FFA0', '#FFA0A0', '#A0A0FF'])
cm_dark = mpl.colors.ListedColormap(['g', 'b', 'r'])
# pcolormesh 绘制背景颜色块(前面取坐标点并获得它们的分类结果就是为了这个)
# 用于区分坐标系中的哪一部分会被分到哪一类
# cmap 自定义颜色(用亮色绘制背景,用暗色绘制测试集中的数据点)
# 绘制测试集中的点
plt.pcolormesh(x1, x2, grid_hat, cmap=cm_light)
plt.scatter(X[:, 0], X[:, 1], c=np.squeeze(y), edgecolor='k', s=50, cmap=cm_dark)
plt.scatter(X_test[:, 0], X_test[:, 1], s=120, facecolor='none', zorder=10)
# 坐标轴标签
plt.xlabel(iris_feature[0], fontsize=20)
plt.ylabel(iris_feature[1], fontsize=20)
# 坐标轴范围
plt.xlim(x1_min, x1_max)
plt.ylim(x2_min, x2_max)
# 坐标轴标题
plt.title('Iris classification based on SVM', fontsize=30)
# 绘图
plt.grid()
plt.show()
ok!画图函数已经完成,完整代码:
# 定义绘图函数(以前两个特征作为分类依据)
def draw1(svm, X):iris_feature = 'sepal length', 'sepal width', 'petal length', 'petal width' # 四个特征# 获取坐标值的范围x1_min, x1_max = X[:, 0].min(), X[:, 0].max()x2_min, x2_max = X[:, 1].min(), X[:, 1].max()# 生成坐标系中的网格点(2D)# 200j,复数,即在这个范围中取 200 个点x1, x2 = np.mgrid[x1_min:x1_max:200j, x2_min:x2_max:200j]# 构造测试点(坐标点)# stack() 方法,将两个二维数组合并成一个新的二维数组,并且数组 1 中的第 i 项和数组 2 中的第 i 项合并为新数组的第 i 项# 输出构造的点的坐标grid_test = np.stack((x1.flat, x2.flat), axis=1)print('坐标点的坐标数据:\n', grid_test)# decision_function 多分类情况# 输出样本到决策超平面的距离(函数间隔),反映属于每个分类的可能性# 第 n 个数是属于第 n 类的可能性# 数越大,说明越有可能属于这个分类z = svm.decision_function(grid_test)print('坐标点到超平面的距离(函数间隔):\n', z)# 预测并输出分类结果,得到 [0, 0, ..., 2, 2]grid_hat = svm.predict(grid_test)print('坐标点预测结果:\n', grid_hat)# 预测并输出测试集中的数据属于每个类别的概率probably = svm.predict_proba(X)print('测试数据的预测概率:\n', probably)# 使得 grid_hat 和 x1 的数组形式一致grid_hat = grid_hat.reshape(x1.shape)cm_light = mpl.colors.ListedColormap(['#A0FFA0', '#FFA0A0', '#A0A0FF'])cm_dark = mpl.colors.ListedColormap(['g', 'b', 'r'])# pcolormesh 绘制背景颜色块(前面取坐标点并获得它们的分类结果就是为了这个)# 用于区分坐标系中的哪一部分会被分到哪一类# cmap 自定义颜色(用亮色绘制背景,用暗色绘制测试集中的数据点)# 绘制测试集中的点plt.pcolormesh(x1, x2, grid_hat, cmap=cm_light)plt.scatter(X[:, 0], X[:, 1], c=np.squeeze(y), edgecolor='k', s=50, cmap=cm_dark)plt.scatter(X_test[:, 0], X_test[:, 1], s=120, facecolor='none', zorder=10)# 坐标轴标签plt.xlabel(iris_feature[0], fontsize=20)plt.ylabel(iris_feature[1], fontsize=20)# 坐标轴范围plt.xlim(x1_min, x1_max)plt.ylim(x2_min, x2_max)# 坐标轴标题plt.title('Iris classification based on SVM', fontsize=30)# 绘图plt.grid()plt.show()
最后得到的准确率是 73% 左右,和我们从图中直观看出来的是差不多的,即只按照花萼长宽进行分类的结果并不很好。
按照花瓣长宽分类和按照花萼长宽分类完全是一个道理,最后画出的图长这样,准确率在 97% 左右,说明对于鸢尾花,花瓣的特征更加鲜明,作为分类依据会更好。
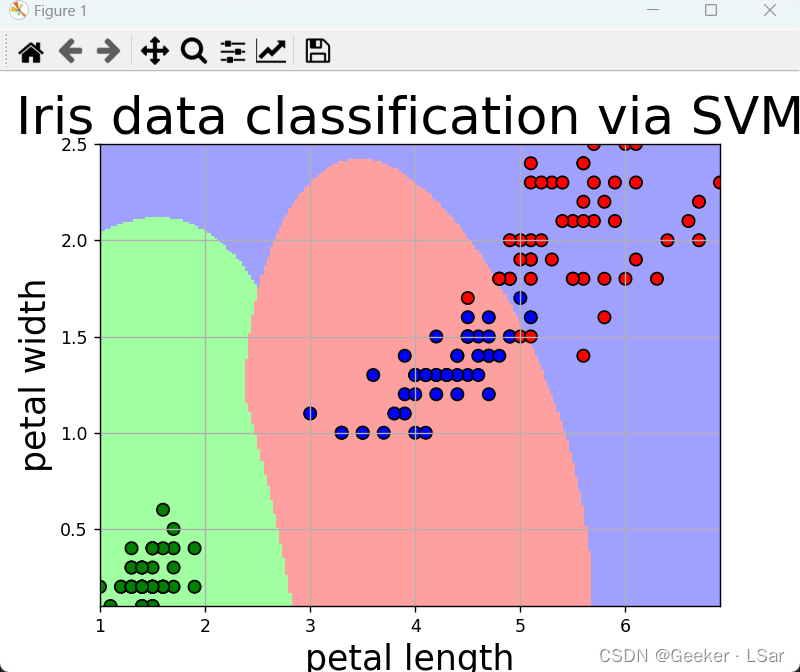
还有一个有趣的结果——按照四个特征分类的准确率居然比只按照花瓣长宽两个特征分类的准确率低(至少在本文的 “实验条件” 下是这样的),可能是因为花萼长宽中的部分数据特征不够鲜明或者有噪声数据(比如某朵花变异了之类的)。
这也说明在训练模型的时候,特征的选取有时并不是越多越好,选取特征的时候需要考虑特征是否鲜明、区分度高。如果特征选取不当,可能会对模型的性能造成负面影响。
ok!以上就是本文的全部内容啦!完整代码:
# 利用支持向量机(SVM)对鸢尾花进行分类,一共分成三类
# Scikit learn 是机器学习中常见的第三方模块,封装了常用算法,包括回归、降维、分类、聚类等
# 鸢尾花数据集:共 150 组数据,每组数据 4 个特征(四维向量)
# matplotlib 用于数据可视化
# numpy 用于科学计算'''第一步,导入各种需要的库'''
import matplotlib.pyplot as plt # 用于数据可视化
import matplotlib as mpl
from sklearn import svm # 引入封装好的 SVM 算法
from sklearn.datasets import load_iris # 引入鸢尾花数据集,共 150 组数据
from sklearn.model_selection import train_test_split # 分割训练集和测试集的函数方法
from sklearn.metrics import accuracy_score # 评判测试准确度的函数方法
import numpy as np # 进行科学计算'''第二步,输出数据集的各种信息并绘制散点图(直观分类)'''
iris = load_iris() # 加载数据集
print(iris.target) # 数据标签(分类结果标签)
print(iris.target_names) # 三种鸢尾花的名字
print(iris.feature_names) # 四个分类特征的名字
X = iris.data # 输入数据(150 个四维向量),样本特征,[n_samples * n_features] 的二维数组
print(X.shape, X) # X.shape,输出 X 数组的行数和列数
y = iris.target # 数据标签 or 分类结果(共三种每种 50 个数据)
print(y.shape, y)
# 以前两个特征(花萼长度、花萼宽度)绘图
X = iris.data[:, :2] # 切片操作,选取前两个特征
plt.scatter(X[y == 0, 0], X[y == 0, 1], color = "red", marker = "o")
plt.scatter(X[y == 1, 0], X[y == 1, 1], color = "green", marker = "+")
plt.scatter(X[y == 2, 0], X[y == 2, 1], color = "blue", marker = "x")
plt.xlabel('sepal length', fontsize=20)
plt.ylabel('sepal width', fontsize=20)
plt.title('Iris names', fontsize=30)
plt.show()
# 以后两个特征(花瓣长度、花瓣宽度)绘图(发现后两个特征能够更好地区分三类鸢尾花)
X = iris.data[:, 2:]
plt.scatter(X[y == 0, 0], X[y == 0, 1], color = "red", marker = "o")
plt.scatter(X[y == 1, 0], X[y == 1, 1], color = "green", marker = "+")
plt.scatter(X[y == 2, 0], X[y == 2, 1], color = "blue", marker = "x")
plt.xlabel('petal length', fontsize=20)
plt.ylabel('petal width', fontsize=20)
plt.title('Iris names', fontsize=30)
plt.show()'''第三步,尝试用不同的方式进行训练'''
# 步骤:
# 1. 获取所需数据集(全部特征 or 某个或某几个特征(切片))
# 2. 定义支持向量机(svm.SVC())
# 3. 划分训练集和测试集(train_test_split())
# 4. 利用训练集进行训练(fit())
# 5. 测试,预测测试集的输出结果(predict())
# 6. 计算测试准确率并输出(accuracy_score())# svm.SVC() 函数是实现 SVM 算法的封装方法之一
# kernel:核函数类型,linear 代表线性,poly 代表多项式,rbf 代表径向基
# C:惩罚系数
# gamma:核函数中的核系数,默认为 1/n_features(特征数的倒数)'''第一类:不分训练集和测试集,用全部特征进行分类'''
X = iris.data
svm1 = svm.SVC(kernel="rbf", C=1, gamma="auto", probability=True)
svm1.fit(X, y) # 用全部特征进行训练
print("训练得分:", svm1.score(X, y))
print("预测:", svm1.predict([[7, 5, 2, 0.5], [7.5, 4, 7, 2]]))
print('\n')'''第二类:分训练集和测试集,训练集训练完后用测试集测试,用全部特征进行分类'''
# test_size 表示训练数据在数据集中的占比,0.2 表示 20%
# random_state 表示随机数种子,改变该值可获得不同的分割方法
svm2 = svm.SVC(kernel="rbf", C=3, gamma="auto", probability=True)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=218)
svm2.fit(X_train, y_train) # 用训练集进行训练
y_predict = svm2.predict(X_test) # 用测试集进行测试
print("准确率:", accuracy_score(y_test, y_predict)) # 计算准确率(正确的所占百分比)
print('\n')'''第三类:分训练集和测试集,用不同特征进行分类'''
# 定义绘图函数(以前两个特征作为分类依据)
def draw1(svm, X):iris_feature = 'sepal length', 'sepal width', 'petal length', 'petal width' # 四个特征# 获取坐标值的范围x1_min, x1_max = X[:, 0].min(), X[:, 0].max()x2_min, x2_max = X[:, 1].min(), X[:, 1].max()# 生成坐标系中的网格点(2D)# 200j,复数,即在这个范围中取 200 个点x1, x2 = np.mgrid[x1_min:x1_max:200j, x2_min:x2_max:200j]# 构造测试点(坐标点)# stack() 方法,将两个二维数组合并成一个新的二维数组,并且数组 1 中的第 i 项和数组 2 中的第 i 项合并为新数组的第 i 项# 输出构造的点的坐标grid_test = np.stack((x1.flat, x2.flat), axis=1)print('坐标点的坐标数据:\n', grid_test)# decision_function 多分类情况# 输出样本到决策超平面的距离(函数间隔),反映属于每个分类的可能性# 第 n 个数是属于第 n 类的可能性# 数越大,说明越有可能属于这个分类z = svm.decision_function(grid_test)print('坐标点到超平面的距离(函数间隔):\n', z)# 预测并输出分类结果,得到 [0, 0, ..., 2, 2]grid_hat = svm.predict(grid_test)print('坐标点预测结果:\n', grid_hat)# 预测并输出测试集中的数据属于每个类别的概率probably = svm.predict_proba(X)print('测试数据的预测概率:\n', probably)# 使得 grid_hat 和 x1 的数组形式一致grid_hat = grid_hat.reshape(x1.shape)cm_light = mpl.colors.ListedColormap(['#A0FFA0', '#FFA0A0', '#A0A0FF'])cm_dark = mpl.colors.ListedColormap(['g', 'b', 'r'])# pcolormesh 绘制背景颜色块(前面取坐标点并获得它们的分类结果就是为了这个)# 用于区分坐标系中的哪一部分会被分到哪一类# cmap 自定义颜色(用亮色绘制背景,用暗色绘制测试集中的数据点)# 绘制测试集中的点plt.pcolormesh(x1, x2, grid_hat, cmap=cm_light)plt.scatter(X[:, 0], X[:, 1], c=np.squeeze(y), edgecolor='k', s=50, cmap=cm_dark)plt.scatter(X_test[:, 0], X_test[:, 1], s=120, facecolor='none', zorder=10)# 坐标轴标签plt.xlabel(iris_feature[0], fontsize=20)plt.ylabel(iris_feature[1], fontsize=20)# 坐标轴范围plt.xlim(x1_min, x1_max)plt.ylim(x2_min, x2_max)# 坐标轴标题plt.title('Iris classification based on SVM', fontsize=30)# 绘图plt.grid()plt.show()# 用前两个特征进行分类
X2 = iris.data[:, :2] # :2 表示取前两个特征,即萼片长和萼片宽
svm3 = svm.SVC(kernel="rbf", C=3, gamma="auto", probability=True)
X2_train, X2_test, y2_train, y2_test = train_test_split(X2, y, test_size=0.3, random_state=218)
svm3.fit(X2_train, y2_train)
y2_predict = svm3.predict(X2_test)
print("准确率:", accuracy_score(y2_test, y2_predict))
draw1(svm3, X2) # 绘图print('\n')
# 定义绘图函数(以后两个特征作为分类依据)
def draw2(svm, X):iris_feature = 'sepal length', 'sepal width', 'petal length', 'petal width' # 四个特征# 获取坐标值的范围x1_min, x1_max = X[:, 0].min(), X[:, 0].max()x2_min, x2_max = X[:, 1].min(), X[:, 1].max()# 生成坐标系中的网格点(2D)# 200j,复数,即在这个范围中取 200 个点x1, x2 = np.mgrid[x1_min:x1_max:200j, x2_min:x2_max:200j]# 构造测试点(坐标点)# stack() 方法,将两个二维数组合并成一个新的二维数组,并且数组 1 中的第 i 项和数组 2 中的第 i 项合并为新数组的第 i 项# 输出构造的点的坐标grid_test = np.stack((x1.flat, x2.flat), axis=1)print('坐标点的坐标数据:\n', grid_test)z = svm.decision_function(grid_test)print('坐标点到超平面的距离(函数间隔):\n', z)# 预测并输出分类结果,得到 [0, 0, ..., 2, 2]grid_hat = svm.predict(grid_test)print('坐标点预测结果:\n', grid_hat)# 预测并输出测试集中的数据属于每个类别的概率probably = svm.predict_proba(X)print('测试数据的预测概率:\n', probably)# 使得 grid_hat 和 x1 的数组形式一致grid_hat = grid_hat.reshape(x1.shape)cm_light = mpl.colors.ListedColormap(['#A0FFA0', '#FFA0A0', '#A0A0FF'])cm_dark = mpl.colors.ListedColormap(['g', 'b', 'r'])# pcolormesh 绘制背景颜色块(前面取坐标点并获得它们的分类结果就是为了这个)# 用于区分坐标系中的哪一部分会被分到哪一类# cmap 自定义颜色(用亮色绘制背景,用暗色绘制测试集中的数据点)# 绘制测试集中的点plt.pcolormesh(x1, x2, grid_hat, cmap=cm_light)plt.scatter(X[:, 0], X[:, 1], c=np.squeeze(y), edgecolor='k', s=50, cmap=cm_dark)plt.scatter(X_test[:, 0], X_test[:, 1], s=120, facecolor='none', zorder=10)# 坐标轴标签plt.xlabel(iris_feature[2], fontsize=20)plt.ylabel(iris_feature[3], fontsize=20)# 坐标轴范围plt.xlim(x1_min, x1_max)plt.ylim(x2_min, x2_max)# 坐标轴标题plt.title('Iris classification based on SVM', fontsize=30)# 绘图plt.grid()plt.show()# 用后两个特征进行分类
X3 = iris.data[:, 2:] # 分割出后两个特征
svm4 = svm.SVC(kernel="rbf", C=3, gamma="auto", probability=True)
X3_train, X3_test, y3_train, y3_test = train_test_split(X3, y, test_size=0.3, random_state=218)
svm4.fit(X3_train, y3_train) # 进行拟合(训练)
y3_predict = svm4.predict(X3_test) # 预测(测试)
print("准确率:", accuracy_score(y3_test, y3_predict)) # 输出测试准确率
draw2(svm4, X3)
ok!!!!!以上就是支持向量机算法的实例!!
嘿嘿真的非常开心你能够看到这里!!一起加油!
如果有任何 bug 欢迎评论区拷打我!!
本文中所有的代码我都做了认真的分析(and 注释),希望对你有所帮助!我们下篇再见!⭐
——Geeker_LStar
相关文章:

【初中生讲机器学习】4. 支持向量机算法怎么用?一个实例带你看懂!
创建时间:2024-02-02 最后编辑时间:2024-02-03 作者:Geeker_LStar 你好呀~这里是 Geeker_LStar 的人工智能学习专栏,很高兴遇见你~ 我是 Geeker_LStar,一名初三学生,热爱计算机和数学,我们一起加…...
CentOS下安装vlc
一、引言 vlc是一跨多媒体播放器,可以播放本地媒体文件和网络串流,帮助我们排查音视频开发过程中遇到的问题。大部分情况下,我们只需要在Windows系统下安装vlc就可以了。但有一种情况是需要在Linux下安装vlc的:我们的音视频拉流软…...

概率论中的全概率公式、贝叶斯公式解析
全概率公式 定义 全概率公式是用来计算一个事件的概率,这个事件可以通过几个互斥事件的并集来表示。这几个互斥事件称为“完备事件系”。实质是由原因推结果。 公式 用途 全概率公式通常用于计算一个事件的总概率,特别是当这个事件与几个不同的因素相关…...

亿赛通-数据泄露防护(DLP)UploadFileList;login接口存在任意文件读取漏洞 附POC软件
@[toc] 亿赛通-数据泄露防护(DLP)UploadFileList;login接口存在任意文件读取漏洞 附POC软件 免责声明:请勿利用文章内的相关技术从事非法测试,由于传播、利用此文所提供的信息或者工具而造成的任何直接或者间接的后果及损失,均由使用者本人负责,所产生的一切不良后果与文…...
如何使用 Google 搜索引擎保姆级教程(附链接)
一、介绍 "Google语法"通常是指在 Google 搜索引擎中使用一系列特定的搜索语法和操作符来精确地定义搜索查询。这些语法和操作符允许用户过滤和调整搜索结果,提高搜索的准确性。 二、安装 Google 下载 Google 浏览器 Google 官网https://www.google.c…...

SpringBoot实现轻量级接口反向代理、转发
目录 1、基本的对象1.1 配置类1.2 实体DTO1.3 路由代理拓展器1.4 请求对象 RestTemplate 2、核心转发代码3、暴露接口4、基础配置 前言:想实现一个轻量级的接口反向代理和转发的一个接口服务,可以通过这个服务做一些需要认证才能访问的接口给到前端使用&…...

算法训练营day21,回溯1
77. 组合 func combine(n int, k int) [][]int { //存储全部集合 result : make([][]int, 0) //存储单次集合 path : make([]int, 0) var backtrace func(n int, k int, startIndex int) backtrace func(n int, k int, startIndex int) { //当单次集合大小和k值相等ÿ…...
婚姻与经济、运动、宗教、科技与经济)
延伸与应用(三)婚姻与经济、运动、宗教、科技与经济
53.幸福婚姻的经济ABC方程式 夫以信先其妇,则妇以信顺其夫。上秉常以化下,下服常而应上,其不化者,百未有一也。 ——《傅子》,傅玄(217—278) 在现代的小家庭中,由于家庭…...

mac上,配置bundletool,将aab转为apk
1.第一步打开终端,安装brew 2.安装bundletool brew install bundletool 3.aab转apk bundletool build-apks --bundle/MyApp/my_app.aab --output/MyApp/my_app.apks 如果下载了bundletool--xxx.jar,脚本命令前加 java -jar bundletool-all-1.5.0.j…...
wangEditor v4的简单使用
当前文档是 wangEditor v4 版本的。 wangEditor v5 已经正式发布,可参考文档。 v5 发布之后,v4 将不再开发新功能。 介绍 English documentation wangEditor4 —— 轻量级 web 富文本编辑器,配置方便,使用简单。 官网&#…...
简单实践 java spring boot 自动配置模拟
1.概要 1.1 需求,自己写一个redis-spring-boot-starter模拟自动配置 自动配置就是在引入*-starter坐标后,可以已经spring框架的规则实现一些Bean的自动注入,并设置一些参数的默认值,且也可以在引入的工程中修改这些配置的值。这…...

BeanDefinition学习
Spring版本5.1.x Spring中的BeanDefinition是一个接口,用于描述Spring容器中Bean的元数据。BeanDefinition描述了Bean的各种属性,如名称、依赖关系、初始化方法等。这个接口通常用于在Spring的IoC容器中注册Bean,并且当容器需要创建Bean实例…...

ASP.NET的GridView控件中,实现同列内容合并
在ASP.NET的GridView控件中,实现同列内容合并的方法主要有两种:一种是使用RowDataBound事件,另一种是使用自定义定义函数 使用RowDataBound事件 这种方法是在GridView的每一行绑定数据时,比较当前行和前一行的同一列的值&#x…...
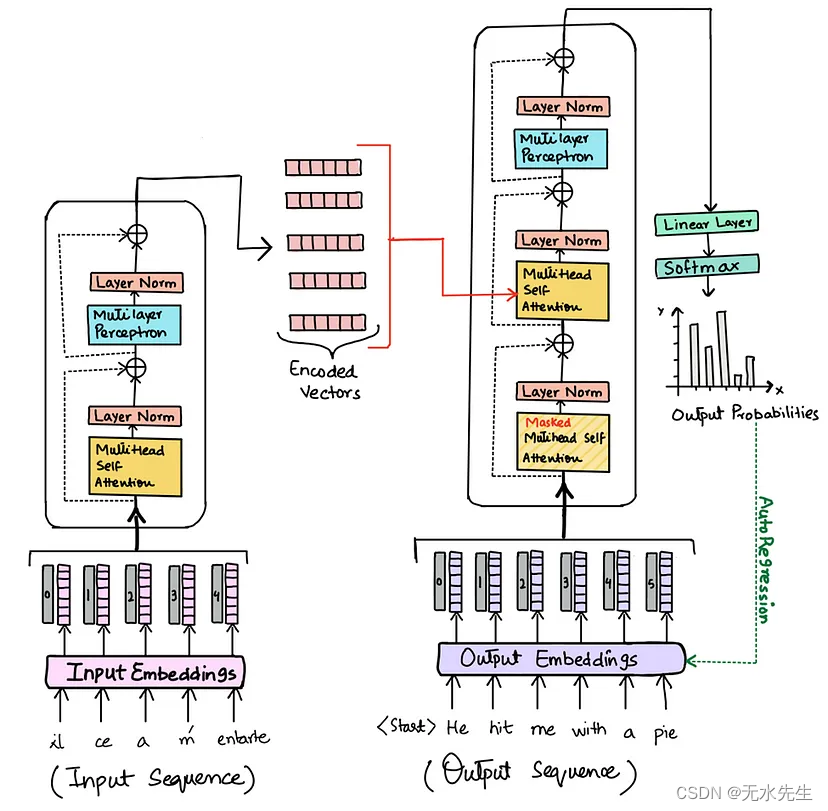
【文本到上下文 #8】NLP中的变形金刚:解码游戏规则改变者
一、说明 欢迎来到我们对不断发展的自然语言处理 (NLP) 领域的探索的第 8 章。在本期中,我们将重点介绍一项重塑 NLP 格局的突破性创新:Transformers。在我们之前对 seq2seq 模型、编码器-解码器框架和注意力机制的讨论之后&#…...

mysql主流版本5.5/5.6/5.7/8.0重置修改密码方法
最近几天来回切换各个Mysql版本重置密码,记录一下各个版本重置密码的方法。 MySql 5.5 SET PASSWORD FOR usernamelocalhost PASSWORD(new_password);MySql5.6 SET PASSWORD FOR usernamelocalhost new_password;MySql5.7 ALTER USER usernamelocalhost IDENT…...

设计模式——备忘录模式
跟多内容,前往IT-BLOG 备忘录模式(Memento Pattern): 保存对象的某个状态,以便在未来需要的时候进行数据的恢复。相当容易理解,举个简单的例子:Word 软件在编辑时按 CtrlZ 组合键时能撤销当…...

深入理解Django与Redis的集成实践
在现代的Web开发中,高效的数据存取和缓存策略是提升应用性能的关键。Django作为一个广泛使用的Python Web框架,提供了丰富的功能以支持高效的Web应用开发。而Redis,作为一个高性能的键值存储系统,常被用于缓存、会话管理等多种场景…...
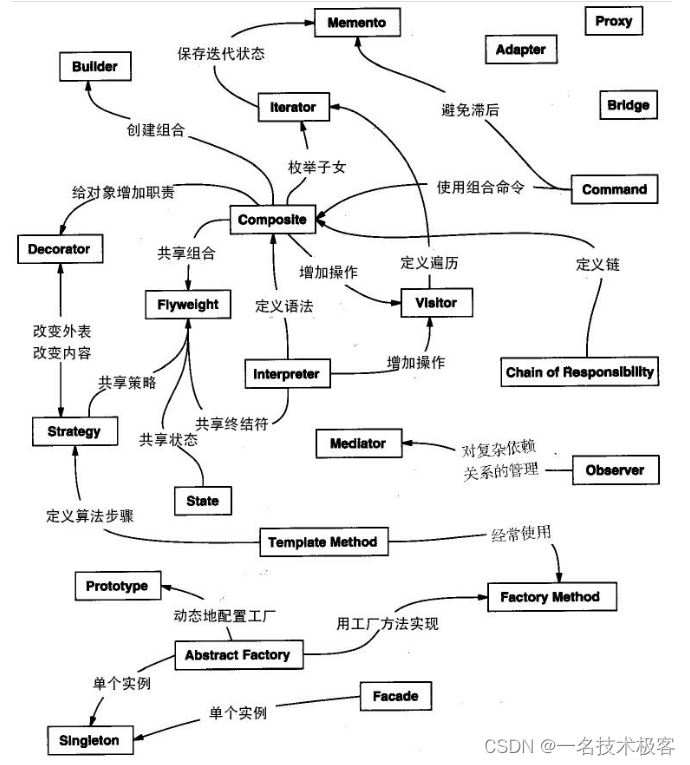
Java设计模式 – 四大类型
设计模式 – 四大类型 创建型模式结构型模式行为型模式J2EE模式 设计模式(Design pattern)是重构解决方案 根据书Design Patterns – Elements of Reusable Object-Oriented Software(中文译名:设计模式 – 可复用的面向对象软件元…...
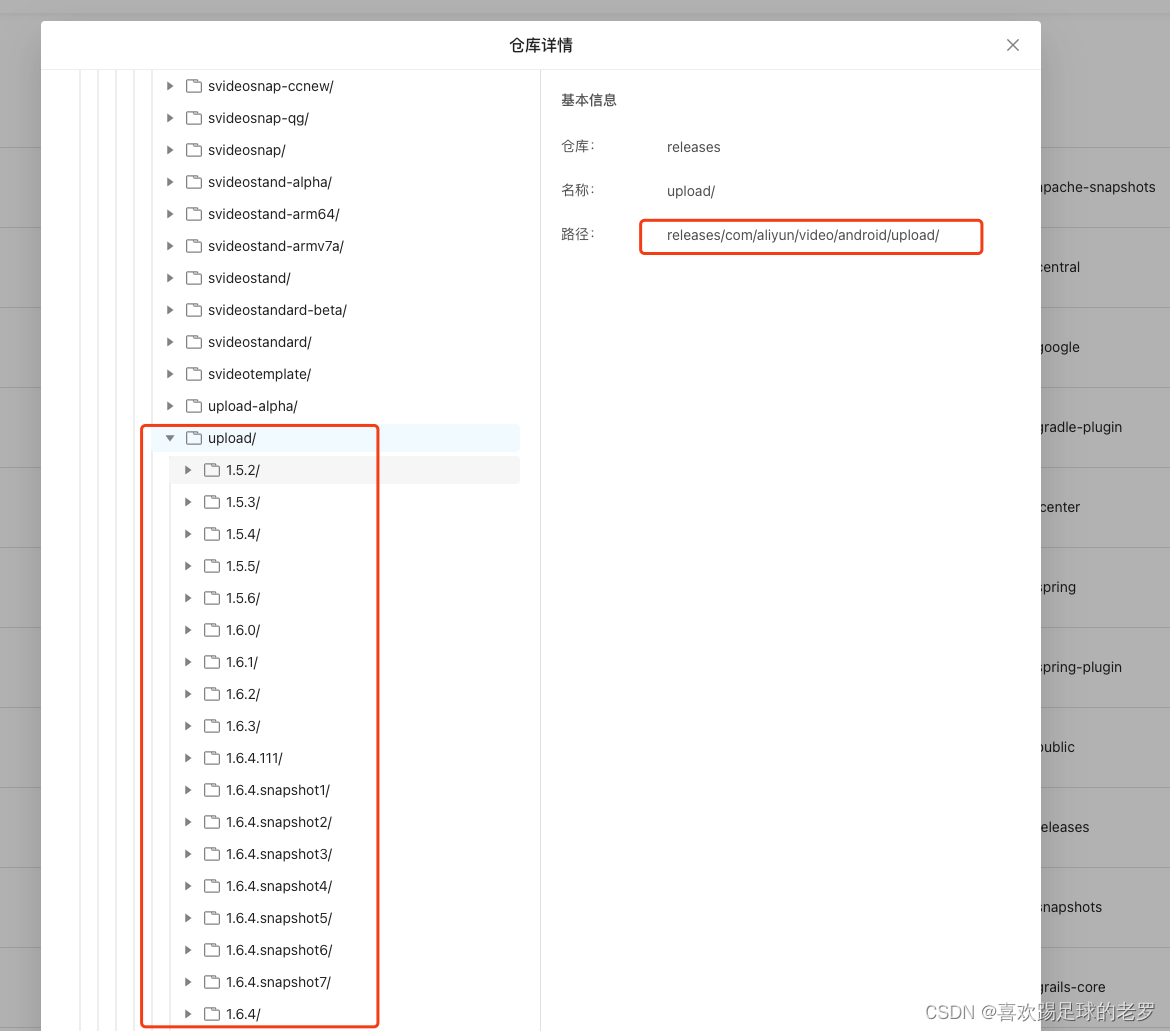
查看阿里云maven仓中某个库有哪些版本
起因 最近项目上有做视频业务,方案是使用阿里云的短视频服务,其中也有使用到阿里云的上传SDK,过程中有遇一个上传SDK的内部崩溃,崩溃栈如下: Back traces starts. java.lang.NullPointerException: Attempt to invok…...
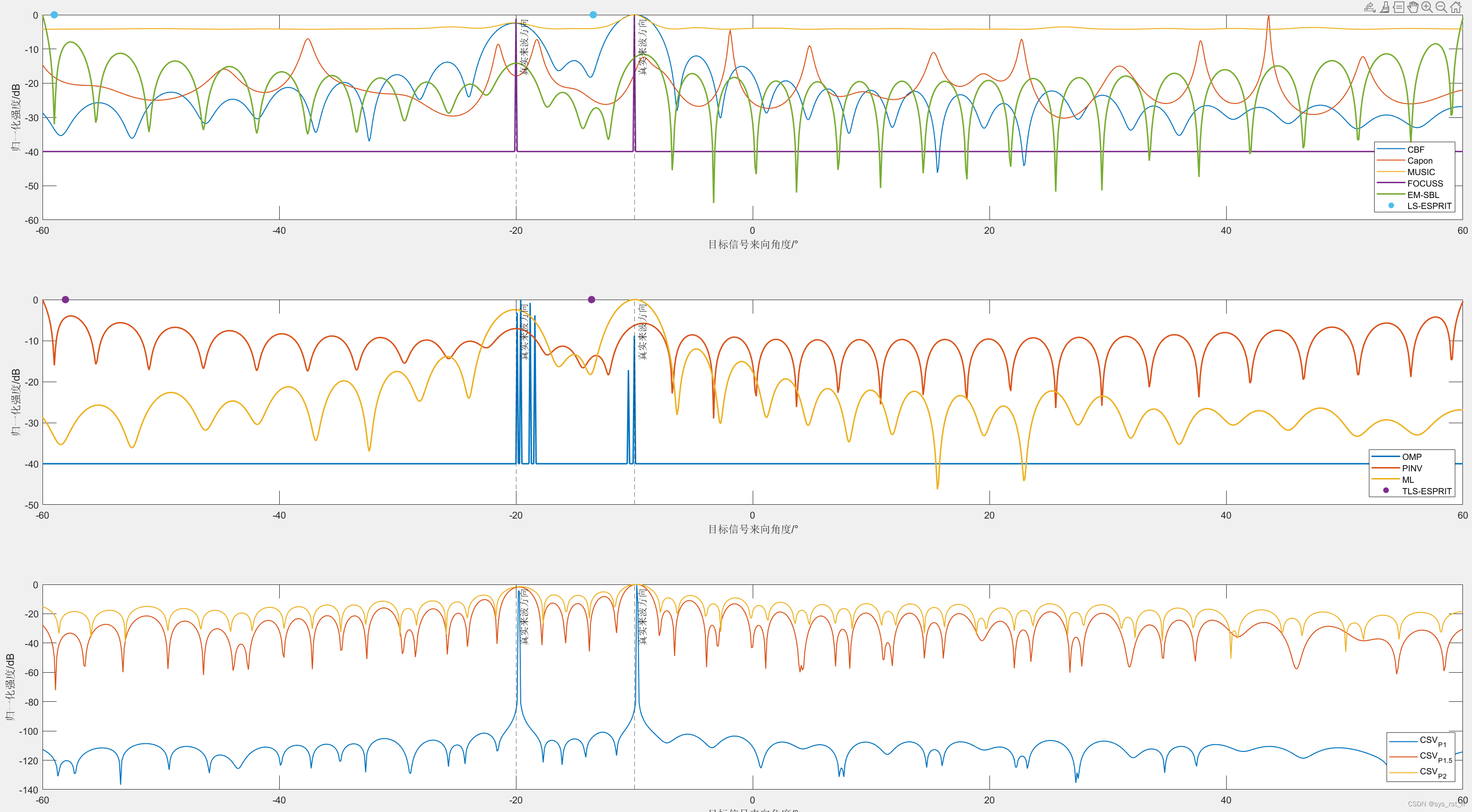
【通信系统】MIMO阵列信号来向DOA估计实现~含FOCUSS、OMP、贝叶斯学习(SBL)等稀疏重构法和常规、子空间法、空间平滑滤波法
MIMO阵列目标信号来向估计原理与实现~基于常规法、子空间变换法和稀疏恢复法 写在最前前言空间谱估计的历史发展 仿真原理离散时间阵列信号模型波束形成矩阵(完备字典)回波生成空间平滑滤波传统方法CBF~常规波束成型Capon~最小方差无失真响应法ML~最大似然估计法 子空间方法MUS…...

云启出海,智联未来|阿里云网络「企业出海」系列客户沙龙上海站圆满落地
借阿里云中企出海大会的东风,以**「云启出海,智联未来|打造安全可靠的出海云网络引擎」为主题的阿里云企业出海客户沙龙云网络&安全专场于5.28日下午在上海顺利举办,现场吸引了来自携程、小红书、米哈游、哔哩哔哩、波克城市、…...

蓝桥杯 2024 15届国赛 A组 儿童节快乐
P10576 [蓝桥杯 2024 国 A] 儿童节快乐 题目描述 五彩斑斓的气球在蓝天下悠然飘荡,轻快的音乐在耳边持续回荡,小朋友们手牵着手一同畅快欢笑。在这样一片安乐祥和的氛围下,六一来了。 今天是六一儿童节,小蓝老师为了让大家在节…...

ESP32读取DHT11温湿度数据
芯片:ESP32 环境:Arduino 一、安装DHT11传感器库 红框的库,别安装错了 二、代码 注意,DATA口要连接在D15上 #include "DHT.h" // 包含DHT库#define DHTPIN 15 // 定义DHT11数据引脚连接到ESP32的GPIO15 #define D…...

令牌桶 滑动窗口->限流 分布式信号量->限并发的原理 lua脚本分析介绍
文章目录 前言限流限制并发的实际理解限流令牌桶代码实现结果分析令牌桶lua的模拟实现原理总结: 滑动窗口代码实现结果分析lua脚本原理解析 限并发分布式信号量代码实现结果分析lua脚本实现原理 双注解去实现限流 并发结果分析: 实际业务去理解体会统一注…...

什么?连接服务器也能可视化显示界面?:基于X11 Forwarding + CentOS + MobaXterm实战指南
文章目录 什么是X11?环境准备实战步骤1️⃣ 服务器端配置(CentOS)2️⃣ 客户端配置(MobaXterm)3️⃣ 验证X11 Forwarding4️⃣ 运行自定义GUI程序(Python示例)5️⃣ 成功效果
Selenium常用函数介绍
目录 一,元素定位 1.1 cssSeector 1.2 xpath 二,操作测试对象 三,窗口 3.1 案例 3.2 窗口切换 3.3 窗口大小 3.4 屏幕截图 3.5 关闭窗口 四,弹窗 五,等待 六,导航 七,文件上传 …...

Kafka主题运维全指南:从基础配置到故障处理
#作者:张桐瑞 文章目录 主题日常管理1. 修改主题分区。2. 修改主题级别参数。3. 变更副本数。4. 修改主题限速。5.主题分区迁移。6. 常见主题错误处理常见错误1:主题删除失败。常见错误2:__consumer_offsets占用太多的磁盘。 主题日常管理 …...

sshd代码修改banner
sshd服务连接之后会收到字符串: SSH-2.0-OpenSSH_9.5 容易被hacker识别此服务为sshd服务。 是否可以通过修改此banner达到让人无法识别此服务的目的呢? 不能。因为这是写的SSH的协议中的。 也就是协议规定了banner必须这么写。 SSH- 开头,…...

大数据治理的常见方式
大数据治理的常见方式 大数据治理是确保数据质量、安全性和可用性的系统性方法,以下是几种常见的治理方式: 1. 数据质量管理 核心方法: 数据校验:建立数据校验规则(格式、范围、一致性等)数据清洗&…...

命令行关闭Windows防火墙
命令行关闭Windows防火墙 引言一、防火墙:被低估的"智能安检员"二、优先尝试!90%问题无需关闭防火墙方案1:程序白名单(解决软件误拦截)方案2:开放特定端口(解决网游/开发端口不通)三、命令行极速关闭方案方法一:PowerShell(推荐Win10/11)方法二:CMD命令…...
