机器学习系列-2 线性回归训练损失
机器学习系列-2 线性回归&训练损失
学习内容来自:谷歌ai学习
https://developers.google.cn/machine-learning/crash-course/framing/check-your-understanding?hl=zh-cn
本文作为学习记录
1 线性回归:
举例:蝉(昆虫物种)在天气炎热的日子里会比在更冷的日子里鸣叫。数十年来,专业和业余科学家一直在编制每分钟的鸣叫声和温度方面的数据。
该图表显示了温度随着鸣叫声次数的增加而上升。 鸣叫声与温度之间的关系是线性关系吗?可以,您可以绘制一条直线来大致说明这种关系:
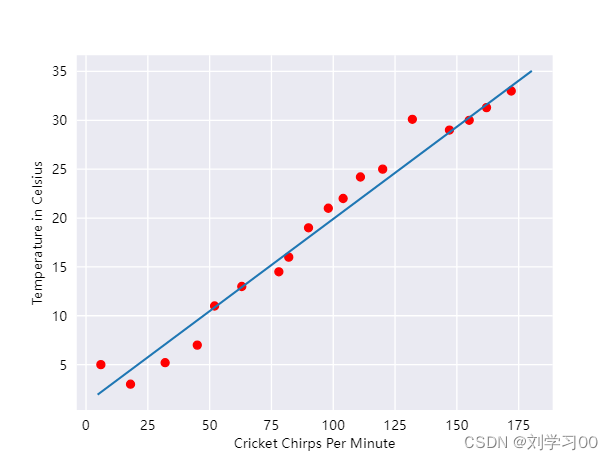
虽然这个直线并未穿过每一个点,但清晰地显示了鸣叫声和温度之间的关系。使用直线的等式,您可以写出这种关系,如下所示:

按照机器学习的惯例,您为模型算式的过程会略有不同:
y = mx + b
y’ = b + w 1 w_{1} w1 x 1 x_{1} x1

其中b为 bias,w为weight
2 训练和损失
训练模型只需从有标签样本中学习(确定)所有权重和偏差的理想值。 在监督式学习中,机器学习算法通过检查许多示例并尝试找到将损失降至最低的模型来构建模型;此过程称为经验风险最小化。
损失是错误预测的惩罚。也就是说,损失是一个表示模型在单个样本上的预测质量的数字。如果模型的预测完全准确,则损失为零,否则损失会更大。训练模型的目的是从所有样本中找到一组平均损失“较小”的权重和偏差。例如,图 3 左侧显示的是高损失模型,右侧显示的是低损失模型。对于该图,请注意以下几点:
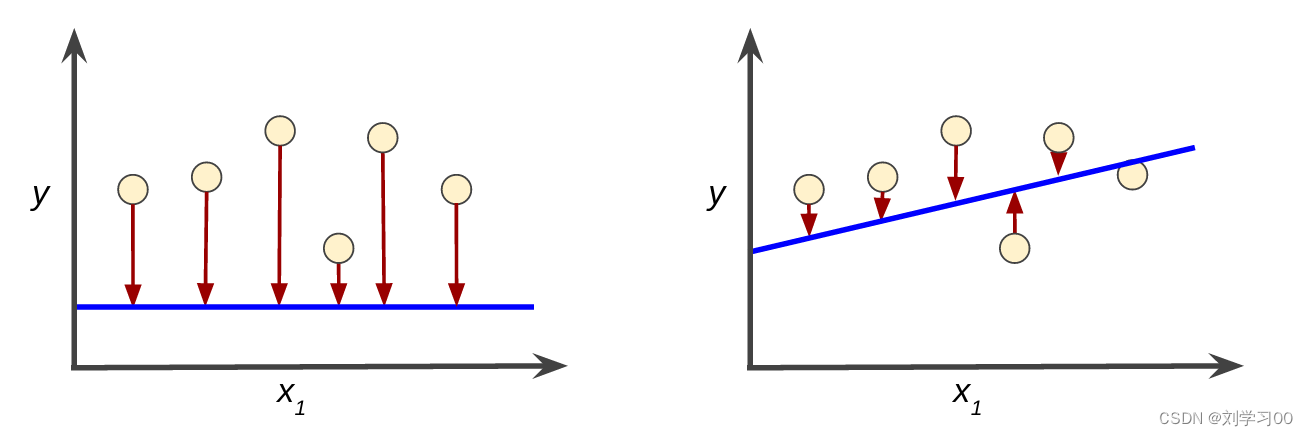
- 箭头表示损失。
- 蓝线表示预测。
图 3. 左侧模型中的损失较高;右侧模型中的损失较低。
2.1 通过创建数学函数(损失函数),以有意义的方式汇总各个损失。
平方损失函数:一种常用的损失函数
我们在此探讨的线性回归模型使用一种称为
| 平方损失函数(也称为L2 损失 ) |
= the square of the difference between the label and the prediction=(标签和预测之间的差值的平方)= (observation - prediction(x))2= (y - y')2
均方误差 (MSE) 是指整个数据集中每个样本的平均平方损失。
如需计算 MSE,请先计算各个样本的所有平方损失之和,然后除以样本数量:

虽然 MSE 常用于机器学习,但它既不是唯一实用的损失函数,也不是适用于所有情况的最佳损失函数。
3.均方误差 (MSE) 的使用举例
均方误差 (MSE) 怎么计算和使用?
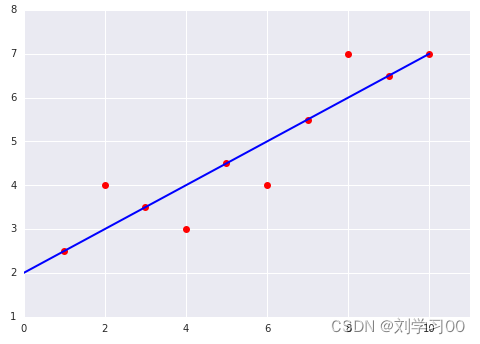
计算:
线上的 6 个示例发生的总损失为 0。四个不在线的样本并未远离离线,因此,即便使它们的平方变平方仍会产生较低的值:
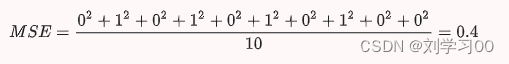
相关文章:
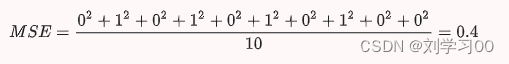
机器学习系列-2 线性回归训练损失
机器学习系列-2 线性回归&训练损失 学习内容来自:谷歌ai学习 https://developers.google.cn/machine-learning/crash-course/framing/check-your-understanding?hlzh-cn 本文作为学习记录1 线性回归: 举例:蝉(昆虫物种&…...

spring-boot-actuator 服务监控
1 概述 服务启动时,通过spring-boot-actuator 监控es等服务是否连接成功等 2 依赖 <!-- 服务监控 --> <dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-actuator</artifactId><…...
窥探向量乘矩阵的存内计算原理—基于向量乘矩阵的存内计算
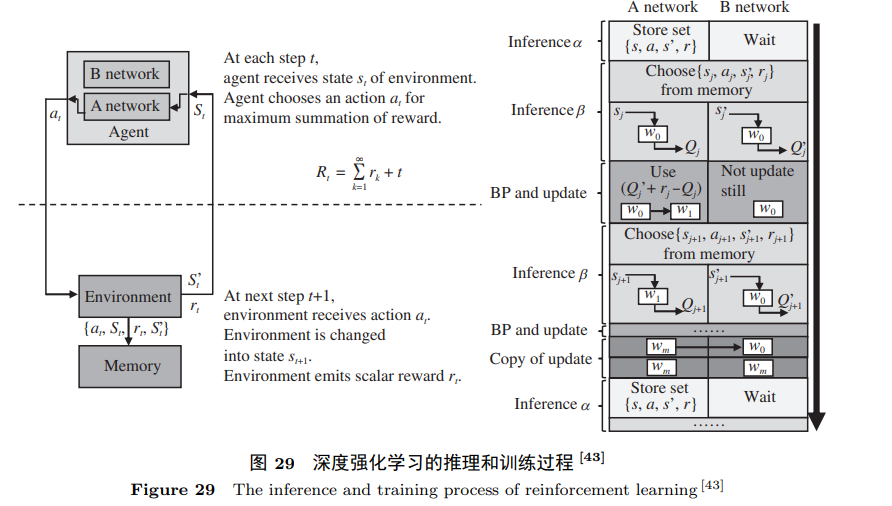
在当今计算领域中,存内计算技术凭借其出色的向量乘矩阵操作效能引起了广泛关注。本文将深入研究基于向量乘矩阵的存内计算原理,并探讨几个引人注目的代表性工作,如DPE、ISAAC、PRIME等,它们在神经网络和图计算应用中表现出色&…...
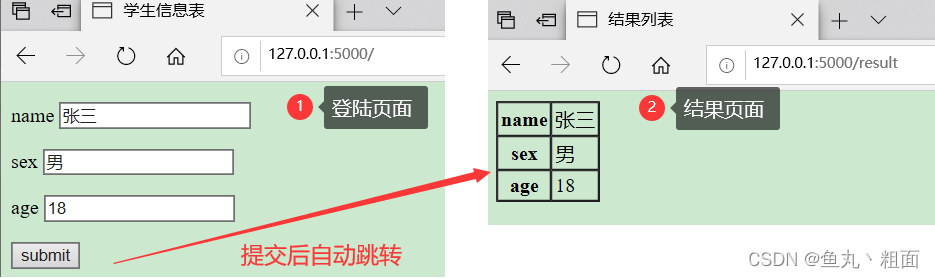
Python flask 表单详解
文章目录 1 概述1.1 request 对象 2 示例2.1 目录结构2.2 student.html2.3 result.html2.4 app.py 1 概述 1.1 request 对象 作用:来自客户端网页的数据作为全局请求对象发送到服务器request 对象的重要属性如下: 属性解释form字典对象,包…...
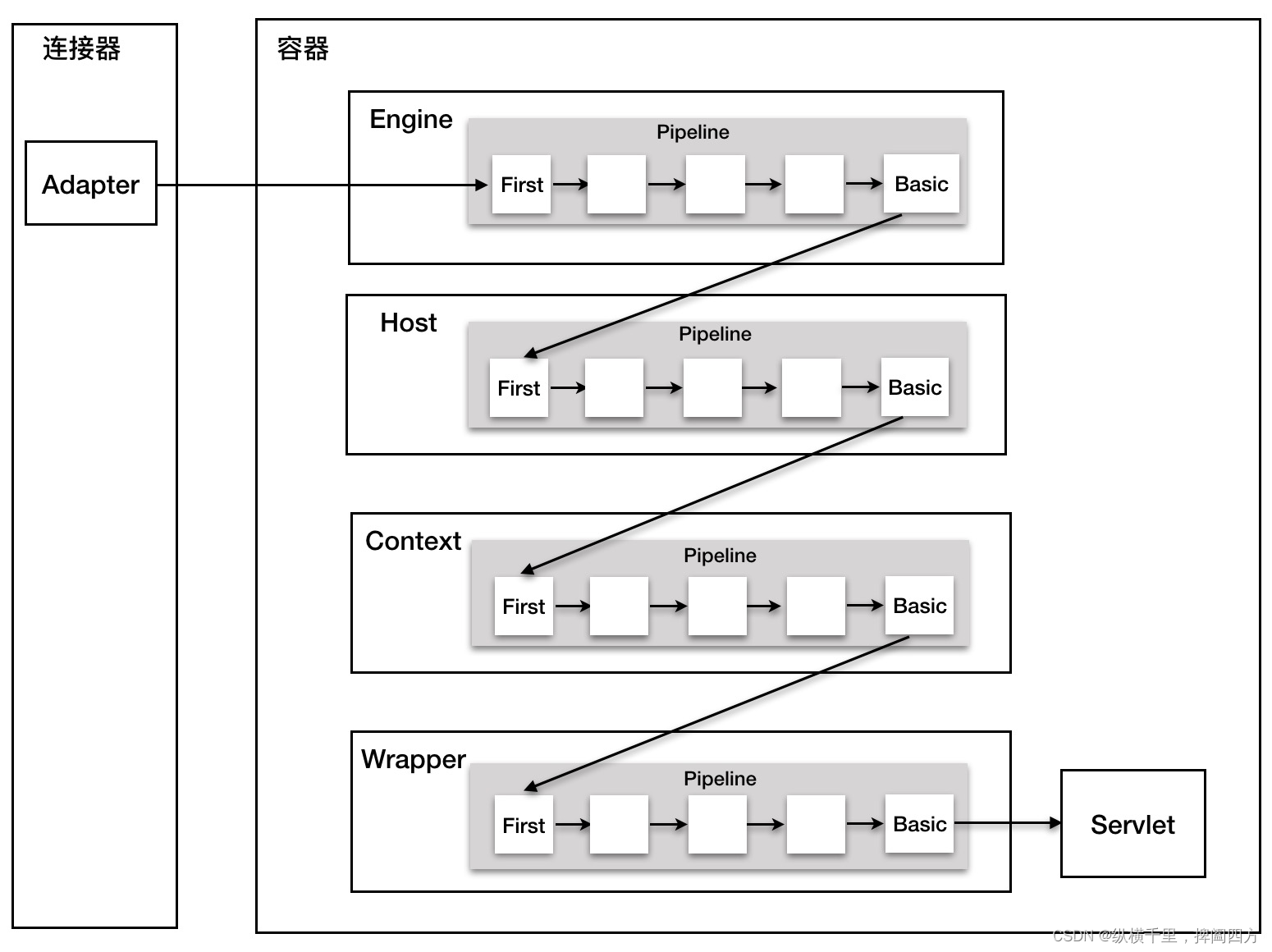
【Tomcat与网络3】Tomcat的整体架构
目录 1.演进1:将连接和处理服务分开 2演进2:Container的演进 3 再论Tomcat的容器结构 4 Tomcat处理请求的过程 5 请求的处理过程与Pipeline-Valve管道 在前面我们介绍了Servlet的基本原理,本文我们结合Tomcat来分析一下如何设计一个大型…...

k8s中cert-manager管理https证书
前言 目前https是刚需,但证书又很贵,虽然阿里云有免费的,但没有泛域名证书,每有一个子域名就要申请一个证书,有效期1年,1年一到全都的更换,太麻烦了。经过搜索,发现了自动更新证书神器cert-manager;当然cert-manager是基于k8s的。 安装采用Helm方式 Chart地址: ht…...

如何搭建私有云盘SeaFile并实现远程访问本地文件资料
🌈个人主页: Aileen_0v0 🔥热门专栏: 华为鸿蒙系统学习|计算机网络|数据结构与算法 💫个人格言:“没有罗马,那就自己创造罗马~” #mermaid-svg-hsDnDEybLME85dTx {font-family:"trebuchet ms",verdana,arial,sans-serif;font-siz…...

Centos7安装Nginx-1.21
一、编译前提,需要安装必要的包 yum install gcc pcre-devel openssl-devel zlib-devel wget -y 二、下载对应的NGINX包 wget http://nginx.org/download/nginx-1.21.0.tar.gz 三、解压nginx tar xf nginx-1.21.0.tar.gz 四、编译并安装nginx到/usr/local/ng…...

React 面试题
1、组件通信的方式 父组件传子组件:通过props 的方式 子组件传父组件:父组件将自身函数传入,子组件调用该函数,父组件在函数中拿到子组件传递的数据 兄弟组件通信:找到共同的父节点,用父节点转发进行通信 …...

Postgresql使用update
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 解决问题一、关联表更新1.关联一张表2.关联多张表 二、根据状态更新为不同的值 解决问题 通过多张关联表更新主表的字段,根据状态更新为不同的值。 一、…...
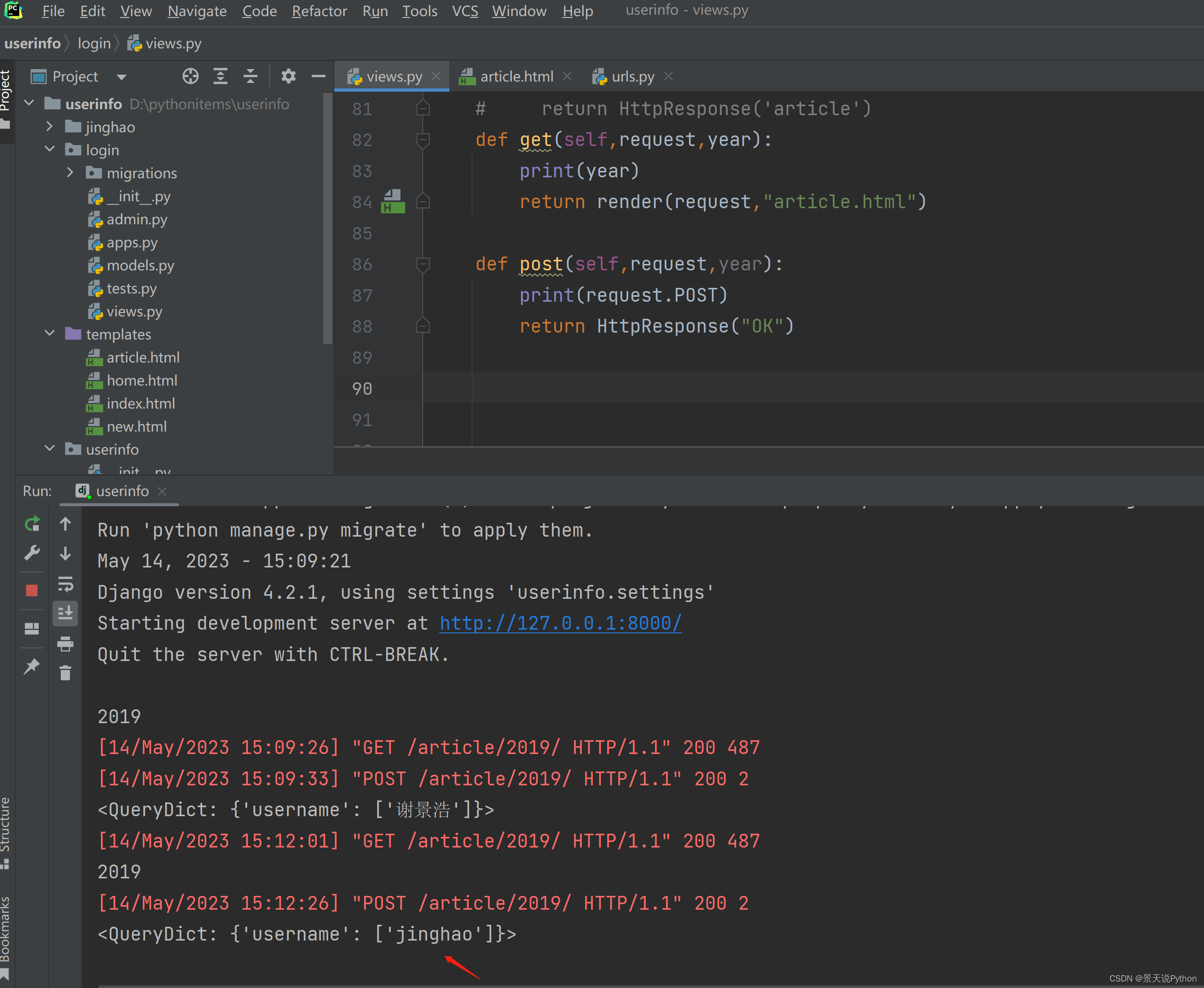
Django视图函数技巧,从入门到实战
文章目录 Django视图函数1.request对象的方法2.视图函数的常用的返回对象(1)response对象(2)JsonResponse对象(3)redirect() :给浏览器了一个30x的状态码 3.设置响应头和状态码(1&am…...
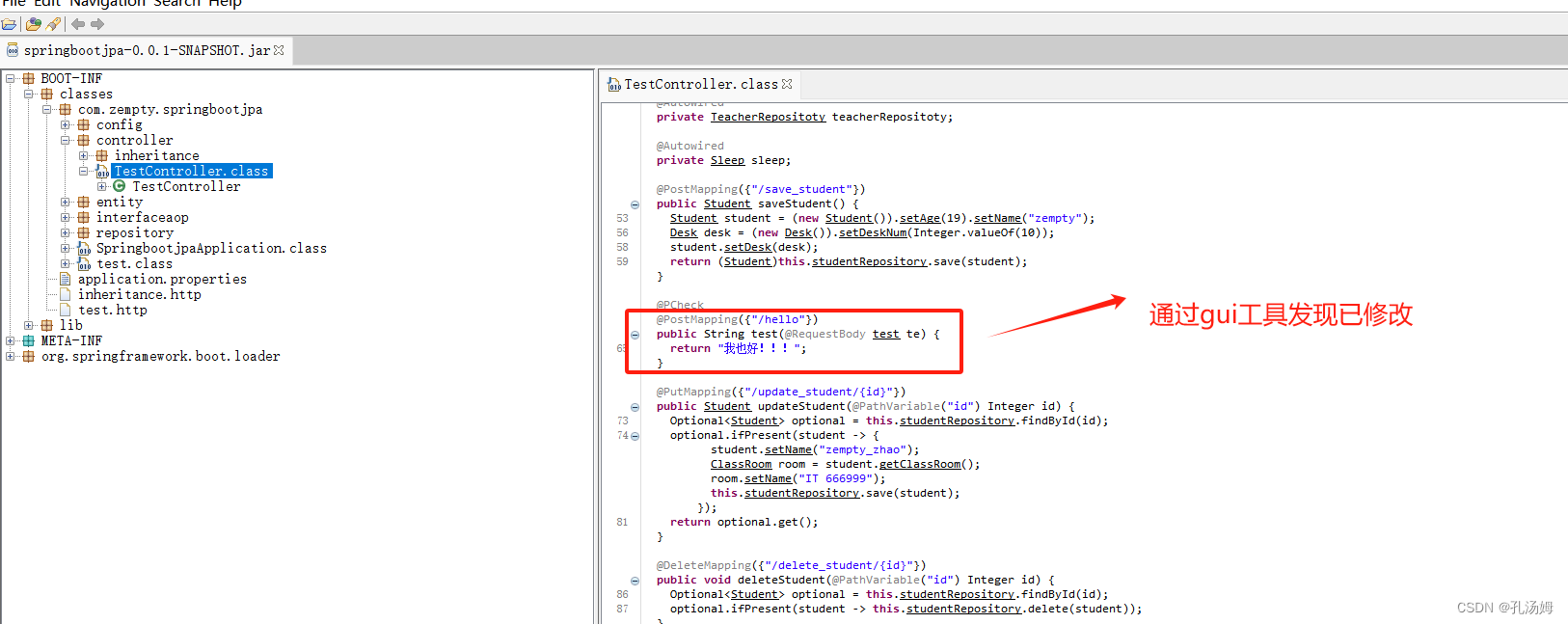
部署实战--修改jar中的文件并重新打包成jar文件
一.jar文件 JAR 文件就是 Java Archive ( Java 档案文件),它是 Java 的一种文档格式JAR 文件与 ZIP 文件唯一的区别就是在 JAR 文件的内容中,多出了一个META-INF/MANIFEST.MF 文件META-INF/MANIFEST.MF 文件在生成 JAR 文件的时候…...
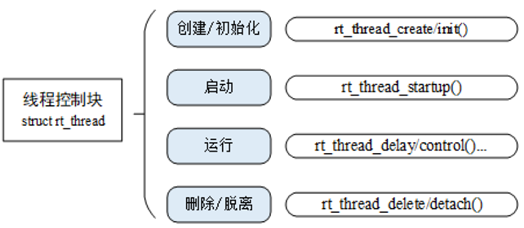
RT-Thread线程管理(使用篇)
layout: post title: “RT-Thread线程管理” date: 2024-1-26 15:39:08 0800 tags: RT-Thread 线程管理(使用篇) 之后会做源码分析 线程是任务的载体,是RTT中最基本的调度单位。 线程执行时的运行环境称为上下文,具体来说就是各个变量和数据,…...
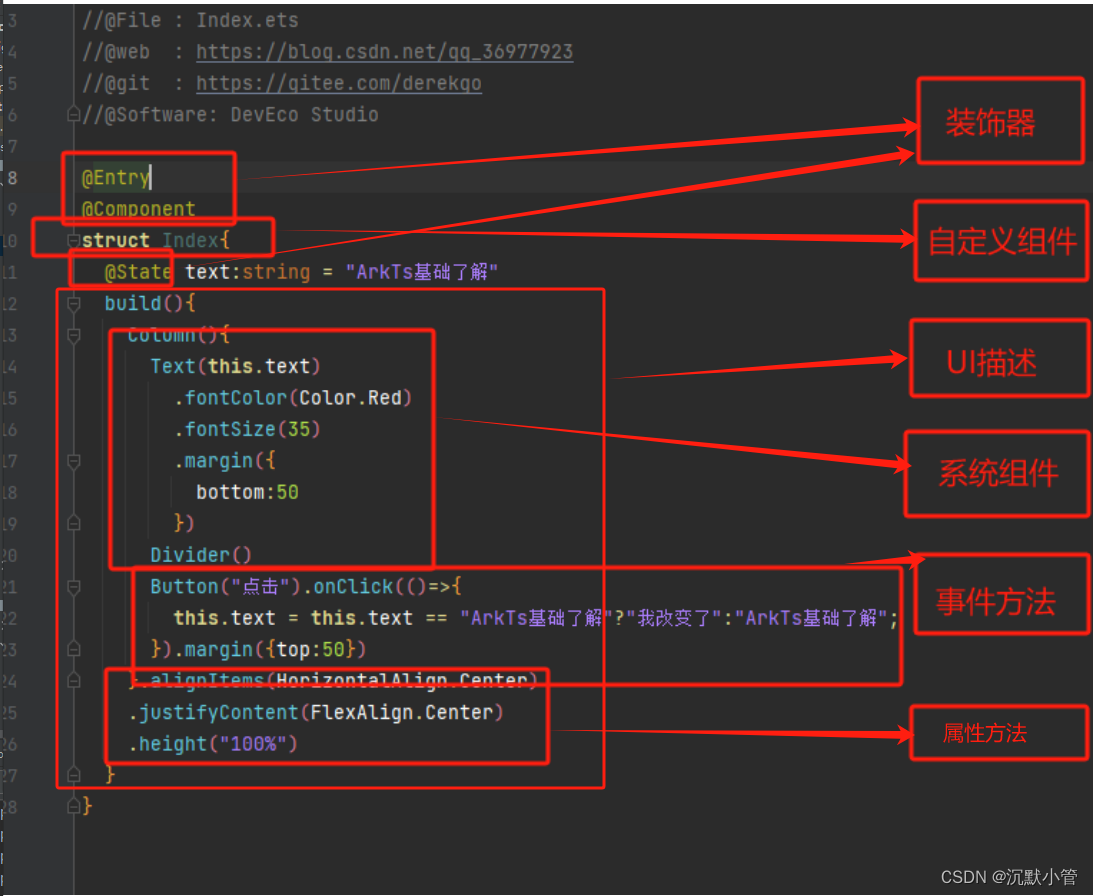
【HarmonyOS】鸿蒙开发之ArkTs初步认识——第2.1章
ArkTs简介 ArkTS是HarmonyOS优选的主力应用开发语言。ArkTS围绕应用开发在TypeScript(简称TS)生态基础上做了进一步扩展,继承了TS的所有特性,是TS的超集。 以下图可以展示Js,TS,ArkTs的关系 ArkTs基础语…...
随手记:uni-app中使用iconfont彩色图标
1、打开阿里巴巴矢量库 2、将下载的压缩文件解压,cmd打开控制台 3、安装npm install -g iconfont-tools(首次使用安装) 4、输入iconfont-tools会生成一个文件夹 5、打开这个文件夹,用里面的相应的css就行...

02-OpenFeign-微服务接入
1、依赖 由于是spring cloud项目,注意spring-boot、cloud、alibaba的版本兼容性 1.1、父级依赖 <properties><java.version>1.8</java.version><spring-boot.version>2.7.18</spring-boot.version><spring.cloud.version>20…...
【前端工程化】环境搭建 nodejs npm
文章目录 前端工程化是什么?前端工程化实现技术栈前端工程化环境搭建 :什么是Nodejs如何安装nodejsnpm 配置和使用npm 介绍npm 安装和配置npm 常用命令 总结 前端工程化是什么? 前端工程化是使用软件工程的方法来单独解决前端的开发流程中模块…...

在VM虚拟机搭建NFS服务器
NFS共享要求如下: (1)共享“/mnt/自已姓名的完整汉语拼音”目录,允许XXX网段的计算机访问该共享目录,可进行读写操作。(说明:XXX网段,请根据你的规划,再具体指定…...
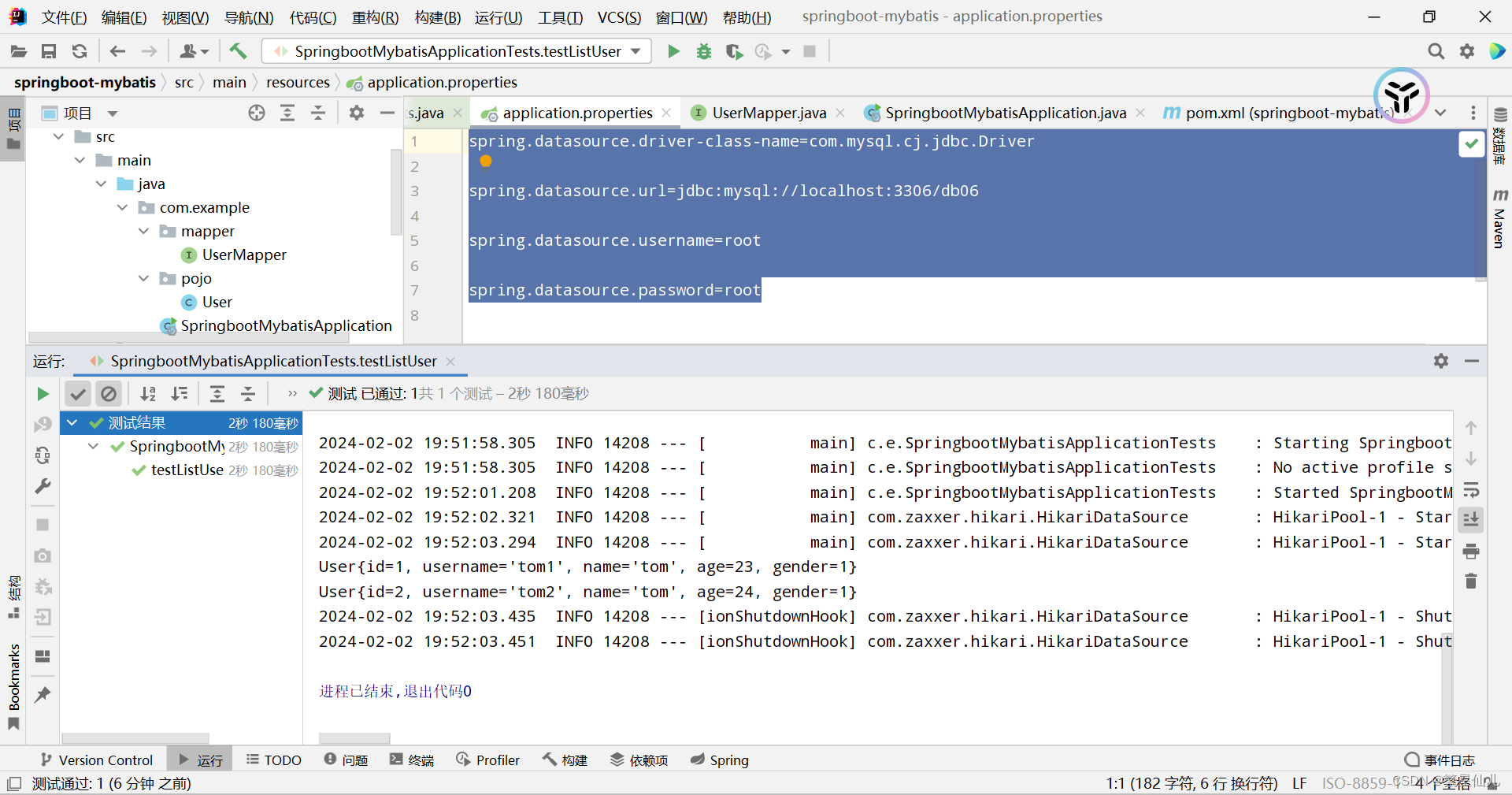
springboot并mybatis入门启动
pom.xml,需要留意jdk的版本(11)和springboot版本要匹配(2.7.4),然后还要注意mybatis启动l类的版本(2.2.2) <?xml version"1.0" encoding"UTF-8"?> <project xm…...

什么是单例模式与饿汉式单例模式的区别是什么?
什么是单例模式与饿汉式单例模式的区别是什么? 单例模式和饿汉式单例模式都是软件设计模式,它们的区别在于实例的创建时间和线程安全性。 单例模式是一种设计模式,确保一个类只有一个实例,并提供一个全局访问点。单例模式可以保…...

TDengine 快速体验(Docker 镜像方式)
简介 TDengine 可以通过安装包、Docker 镜像 及云服务快速体验 TDengine 的功能,本节首先介绍如何通过 Docker 快速体验 TDengine,然后介绍如何在 Docker 环境下体验 TDengine 的写入和查询功能。如果你不熟悉 Docker,请使用 安装包的方式快…...

逻辑回归:给不确定性划界的分类大师
想象你是一名医生。面对患者的检查报告(肿瘤大小、血液指标),你需要做出一个**决定性判断**:恶性还是良性?这种“非黑即白”的抉择,正是**逻辑回归(Logistic Regression)** 的战场&a…...

从零实现富文本编辑器#5-编辑器选区模型的状态结构表达
先前我们总结了浏览器选区模型的交互策略,并且实现了基本的选区操作,还调研了自绘选区的实现。那么相对的,我们还需要设计编辑器的选区表达,也可以称为模型选区。编辑器中应用变更时的操作范围,就是以模型选区为基准来…...

【2025年】解决Burpsuite抓不到https包的问题
环境:windows11 burpsuite:2025.5 在抓取https网站时,burpsuite抓取不到https数据包,只显示: 解决该问题只需如下三个步骤: 1、浏览器中访问 http://burp 2、下载 CA certificate 证书 3、在设置--隐私与安全--…...
:邮件营销与用户参与度的关键指标优化指南)
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南 在数字化营销时代,邮件列表效度、用户参与度和网站性能等指标往往决定着创业公司的增长成败。今天,我们将深入解析邮件打开率、网站可用性、页面参与时…...

dify打造数据可视化图表
一、概述 在日常工作和学习中,我们经常需要和数据打交道。无论是分析报告、项目展示,还是简单的数据洞察,一个清晰直观的图表,往往能胜过千言万语。 一款能让数据可视化变得超级简单的 MCP Server,由蚂蚁集团 AntV 团队…...

深度学习习题2
1.如果增加神经网络的宽度,精确度会增加到一个特定阈值后,便开始降低。造成这一现象的可能原因是什么? A、即使增加卷积核的数量,只有少部分的核会被用作预测 B、当卷积核数量增加时,神经网络的预测能力会降低 C、当卷…...

使用LangGraph和LangSmith构建多智能体人工智能系统
现在,通过组合几个较小的子智能体来创建一个强大的人工智能智能体正成为一种趋势。但这也带来了一些挑战,比如减少幻觉、管理对话流程、在测试期间留意智能体的工作方式、允许人工介入以及评估其性能。你需要进行大量的反复试验。 在这篇博客〔原作者&a…...

uniapp 字符包含的相关方法
在uniapp中,如果你想检查一个字符串是否包含另一个子字符串,你可以使用JavaScript中的includes()方法或者indexOf()方法。这两种方法都可以达到目的,但它们在处理方式和返回值上有所不同。 使用includes()方法 includes()方法用于判断一个字…...

day36-多路IO复用
一、基本概念 (服务器多客户端模型) 定义:单线程或单进程同时监测若干个文件描述符是否可以执行IO操作的能力 作用:应用程序通常需要处理来自多条事件流中的事件,比如我现在用的电脑,需要同时处理键盘鼠标…...
