numpy学习总结二
单词发音:
squeeze 发音:死贵子
concatenation [kɒnˌkætəˈneɪʃən] 拼接;串联
threshold ['θreʃhəʊld] 死re后的
quantile 拷n太哦 分位数
因果不能改
智慧不能赐
正法不可说
无缘不能度
天雨虽宽不润无根之草;佛法虽广不度无缘之人
1)某一个维度,实现元素复值
import numpy as np
arr = np.random.randint(1, 10, (2, 3))
print(arr)
print(arr.repeat(2, axis=0)) # 行复制,列不变 结果: 4行3列
print(arr.repeat(2, axis=1)) # 列复制,行不变 结果: 2行6列
实现按块复制元素
import numpy as np
arr = np.random.randint(1, 10, (2, 3))
print(np.tile(arr, 2)) # 按块复制
print(np.tile(arr, (2, 1))) # 按块当成一个元素(一个整体) 2行1列
print(np.tile(arr, (1, 2))) # 按块当成一个元素 1行2列
水平或竖直方向合并多个数组 (两种方法合并)
import numpy as np
arr1 = np.random.randint(1, 10, (2, 3))
arr2 = np.random.randint(1, 10, (3, 3))
print(arr1)
print(arr2)
print(‘*’ * 30)
目标: 合并 5行3列
print(np.vstack((arr1, arr2))) # 必须是以元组的形式传入
print(np.hstack((arr1, arr2[:2, :]))) # arr2[:2, :]意思是: 行是选2行,列是全选,本案例编程2行3列
指定维度上的合并
print(np.concatenate((arr1, arr2))) # 默认是垂直方向
print(np.concatenate((arr1, arr2[:2, :]), axis=1)) # 水平方向合并
r_和c_的使用
print(np.r_[arr1, arr2]) # 行合并
print(np.c_[arr1, arr2[:2, :]]) # 列合并
返回数组中某个维度的最大或者最小值索引
import numpy as np
arr = np.random.randint(1, 10, (2, 3))
print(arr)
print(arr.argmax()) # 按照行展平了之后的最大值
print(arr.argmin()) # 按照行展平了之后的最小值
print(arr.argmax(axis=1)) # 某一维度最大值axis=0/1, 本例应该返回3个值
限制打印元素的个数
import numpy as np
import sys
print(sys.maxsize)
np.set_printoptions(threshold=sys.maxsize) # 全部打印
print(np.arange(100))
np.set_printoptions(precision=3) # 3位有效数字
print(np.linspace(0, 10, 100))
返回一个有规律的数组,如数组: [1, 1, 1, 2, 2, 2, 3, 3, 3, 1, 2, 3, 1, 2, 3, 1, 2, 3]
import numpy as np
a = np.array([1, 2, 3])
print(a)
print(np.repeat(a, 3))
print(np.tile(a, 3))
最终结果如下:
print(np.r_[np.repeat(a, 3), np.tile(a, 3)])
print(np.hstack((np.repeat(a, 3), np.tile(a, 3))))
print(np.concatenate((np.repeat(a, 3), np.tile(a, 3)), axis=0))
列表实现向量化
import numpy as np
a = [1, 2, 3]
print(np.array(a) + 1) # 这就是向量化操作
def add(x, y):
return x + y
addNum = np.vectorize(add) # 用vectorize做了一层包装
ret = addNum(a, 1)
print(ret)
ret2 = addNum([1, 2, 3], [5, 5, 5]) # 两个列表相加
print(ret2)
求中位数和众数
import numpy as np
中位数是指将数据按⼤⼩顺序排列起来,形成⼀个数列,居于数列中间位置的那个数据。
如果数组是偶数,则是两个数的平均值
众数是在⼀组数据中,出现次数最多的数据 通过bincount和argmax求众数
arr = np.random.randint(1, 10, (10,))
print(arr)
print(np.median(arr)) # 求中位数
tmp = np.bincount(arr)
print(np.argmax(tmp)) # [0 1 0 1 4 2 0 0 1 1] 每个数据出现的次数统计
求任意分位数(也叫分为点)
import numpy as np
arr = np.random.randint(1, 10, (15,))
print(np.median(arr))
print(np.sort(arr)) # 分位数肯定是先sort之后的值
print(‘*’ * 30)
print(np.percentile(arr, q=50)) # np.percentile(arr, q=50) == np.median(arr)
print(np.percentile(arr, q=[1, 25, 50, 75, 100])) # 求一组分位数
求相关系数,是研究变量之间线性相关程度的量;
import numpy as np
arr = np.array([[1, 2], [2, 3.8]]) # 线性相关性
print(arr)
print(np.corrcoef(arr[:, 0], arr[:, 1])) # 考靠负
找到NumPy中缺失值
import numpy as np
np.nan # nan not number
arr = np.array([0., 1., np.nan,
3., np.nan, np.nan, 6., 7., 8., 9.])
用isnan和where两个函数,可以定位哪个位置是空值,通过where查看哪些位置
print(np.where(np.isnan(arr)))
缺失值默认填0
import numpy as np
arr = np.array([[0., np.nan, 2., 3.],
[4., 5., np.nan, 7.],
[8., 9., 10., 11.],
[12., 13., np.nan, 15.],
[16., 17., np.nan, 19.],
[20., 21., 22., 23.]])
print(np.where(np.isnan(arr)))
arr[np.isnan(arr)] = 0 # ~np.isnan(arr),取反就是不为0的
print(arr)
返回无缺失的行
import numpy as np
arr = np.array([[0., np.nan, 2., 3.],
[4., 5., np.nan, 7.],
[8., 9., 10., 11.],
[12., 13., np.nan, 15.],
[16., 17., np.nan, 19.],
[20., 21., 22., 23.]])
返回有缺失值的行
m = np.sum(np.isnan(arr), axis=1) == 0
print(arr[m])
求softmax得分值
import numpy as np
arr = np.array([1, 3, 2, 4])
print(arr)
def softmax(a):
e_a = np.exp(a - np.max(a))
return e_a / np.sum(e_a)
np.set_printoptions(precision=3)
sf = softmax(arr)
print(sf)
相关文章:

numpy学习总结二
单词发音: squeeze 发音:死贵子 concatenation [kɒnˌktəˈneɪʃən] 拼接;串联 threshold [θreʃhəʊld] 死re后的 quantile 拷n太哦 分位数 因果不能改 智慧不能赐 正法不可说 无缘不能度 天雨虽宽不润无根之草;佛法虽广不度无缘之人 …...
3 编辑器(Vim)
1.完成 vimtutor。备注:它在一个 80x24(80 列,24 行) 终端窗口看起来效果最好。 2.下载我们提供的 vimrc,然后把它保存到 ~/.vimrc。 通读这个注释详细的文件 (用 Vim!), 然后观察 …...

C/C++ (stdio.h)标准库详解
cstdio,在C语言中称为stdio.h。该库使用所谓的流与物理设备(如键盘、打印机、终端)或系统支持的任何其他类型的文件一起操作。 在本文将会通过介绍函数参数,举出实际的简单例子来帮助大家快速上手使用函数。 目录 一、流 二、库函数 1、F…...

深度学习介绍
对于具备完善业务逻辑的任务,大多数情况下,正常的人都可以给出一个符合业务逻辑的应用程序。但是对于一些包含超过人类所能考虑到的逻辑的任务,例如面对如下任务: 编写一个应用程序,接受地理信息、卫星图像和一些历史…...
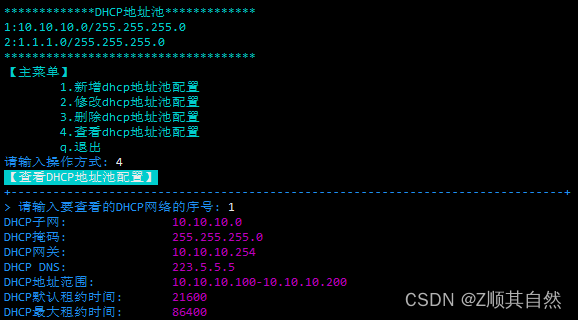
ywtool dhcp命令
一.dhcp功能介绍 就是通过脚本实现dhcp地址池的增、删、改、查这几个功能日志文件路径: /var/log/ywtools/ywtool-dhcp.log/usr/local/ywtools/config/config.ini中account参数(ywtool dhcp这个命令用的,但是这个命令只能配置1个地址池,所以这里面的参数没什么意义) 二.配置…...
)
ChatGPT高效提问—基础知识(LM、PLM以及LLM)
ChatGPT高效提问—基础知识(LM、PLM以及LLM) 了解语言模型(language model, LM)、预训练语言模型(pre-trained language model, PLM)和大型语言模型(large language model, LLM)…...
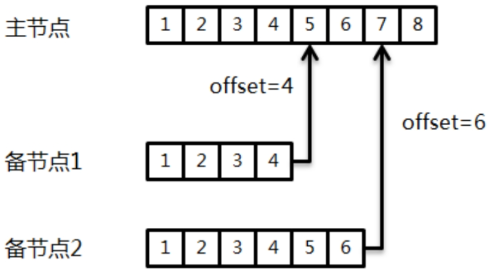
MongoDB复制集实战及原理分析
文章目录 MongoDB复制集复制集架构三节点复制集模式PSS模式(官方推荐模式)PSA模式 典型三节点复制集环境搭建复制集注意事项环境准备配置复制集复制集状态查询使用mtools创建复制集安全认证复制集连接方式 复制集成员角色属性一:Priority 0属…...
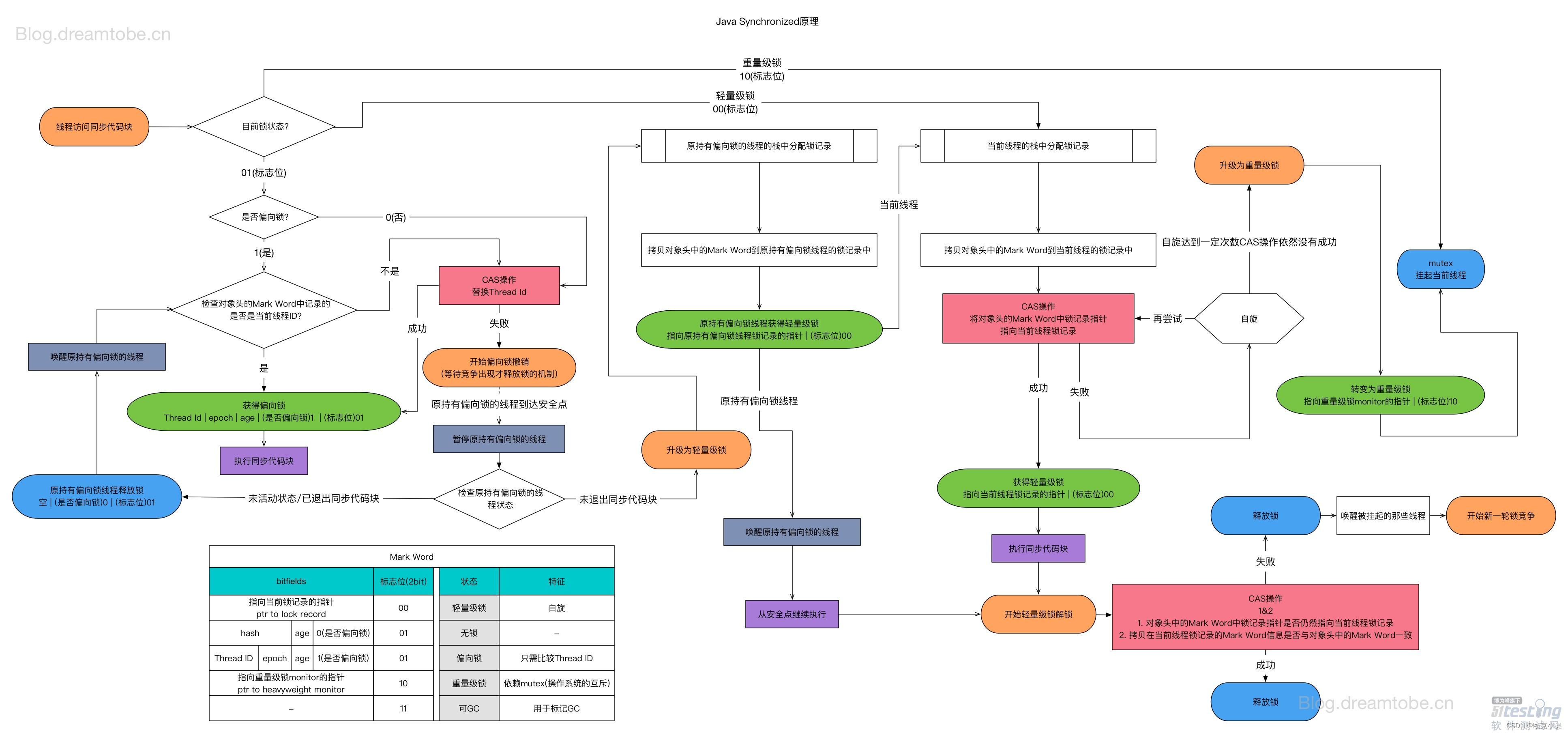
Java并发之synchronized详解
☆* o(≧▽≦)o *☆嗨~我是小奥🍹 📄📄📄个人博客:小奥的博客 📄📄📄CSDN:个人CSDN 📙📙📙Github:传送门 📅&a…...

Flask 项目自动生成 API 文档的高效实践
Flasgger,作为一款强大的 Flask 扩展,自动从 Flask 应用中提取并生成 OpenAPI 规范文档,配备 SwaggerUI,为开发者提供了一条快捷通道,让 API 的文档编制和交互式测试变得简单易行。Flasgger 的设计原则是简化开发流程&…...
WebChat——一个开源的聊天应用
Web Chat 是开源的聊天系统,支持一键免费部署私人Chat网页的应用程序。 开源地址:https://github.com/loks666/webchat 目录树 TOC 👋🏻 开始使用 & 交流🛳 开箱即用 A 使用 Docker 部署B 使用 Docker-compose…...
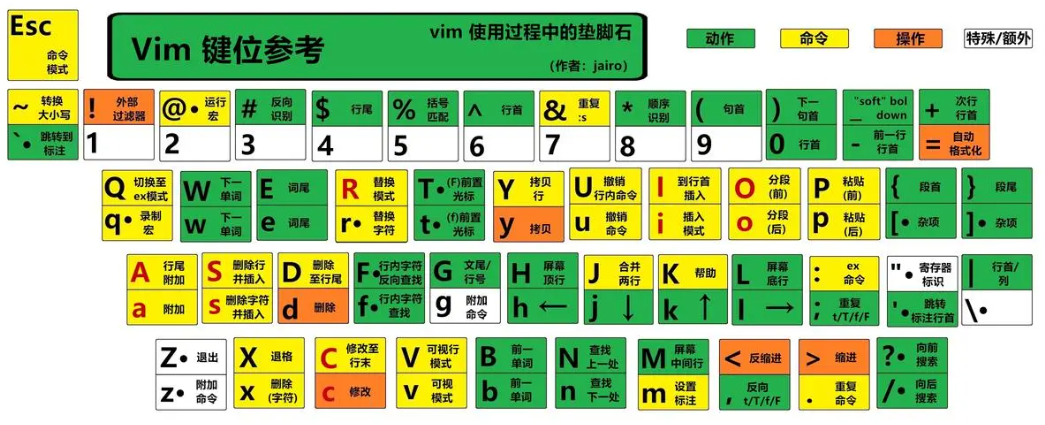
【Linux系统 01】Vim工具
目录 一、Vim概述 1. 文件打开方式 2. 模式切换 二、命令模式 1. 移动与跳转 2. 复制与粘贴 3. 剪切与撤销 三、编辑模式 1. 插入 2. 替换 四、末行模式 1. 保存与退出 2. 查找与替换 3. 分屏显示 4. 命令执行 一、Vim概述 1. 文件打开方式 vim 文件路径&#…...

Oracle 面试题 | 09.精选Oracle高频面试题
🤍 前端开发工程师、技术日更博主、已过CET6 🍨 阿珊和她的猫_CSDN博客专家、23年度博客之星前端领域TOP1 🕠 牛客高级专题作者、打造专栏《前端面试必备》 、《2024面试高频手撕题》 🍚 蓝桥云课签约作者、上架课程《Vue.js 和 E…...
基于Springboot的校园失物招领网站(有报告)。Javaee项目,springboot项目。
演示视频: 基于Springboot的校园失物招领网站(有报告)。Javaee项目,springboot项目。 项目介绍: 采用M(model)V(view)C(controller)三层体系结构…...
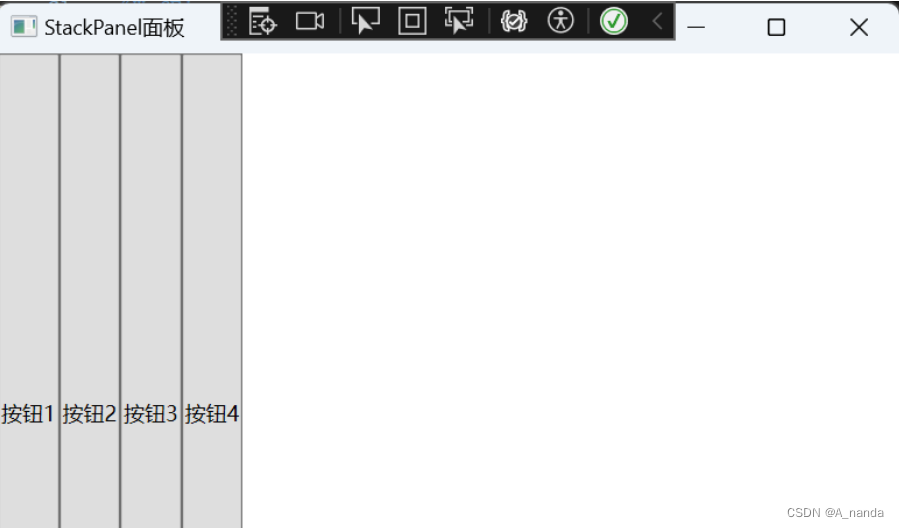
WPF布局面板
StackPanel StackPanel 是一种常用的布局控件,可以支持水平或垂直排列,但不会换行。当子元素添加到 StackPanel 中时,它们将按照添加的顺序依次排列。默认情况下,StackPanel 的排列方向是垂直的,即子元素将从上到下依次排列。可以使用 Orientation 属性更改排列方向。可以…...
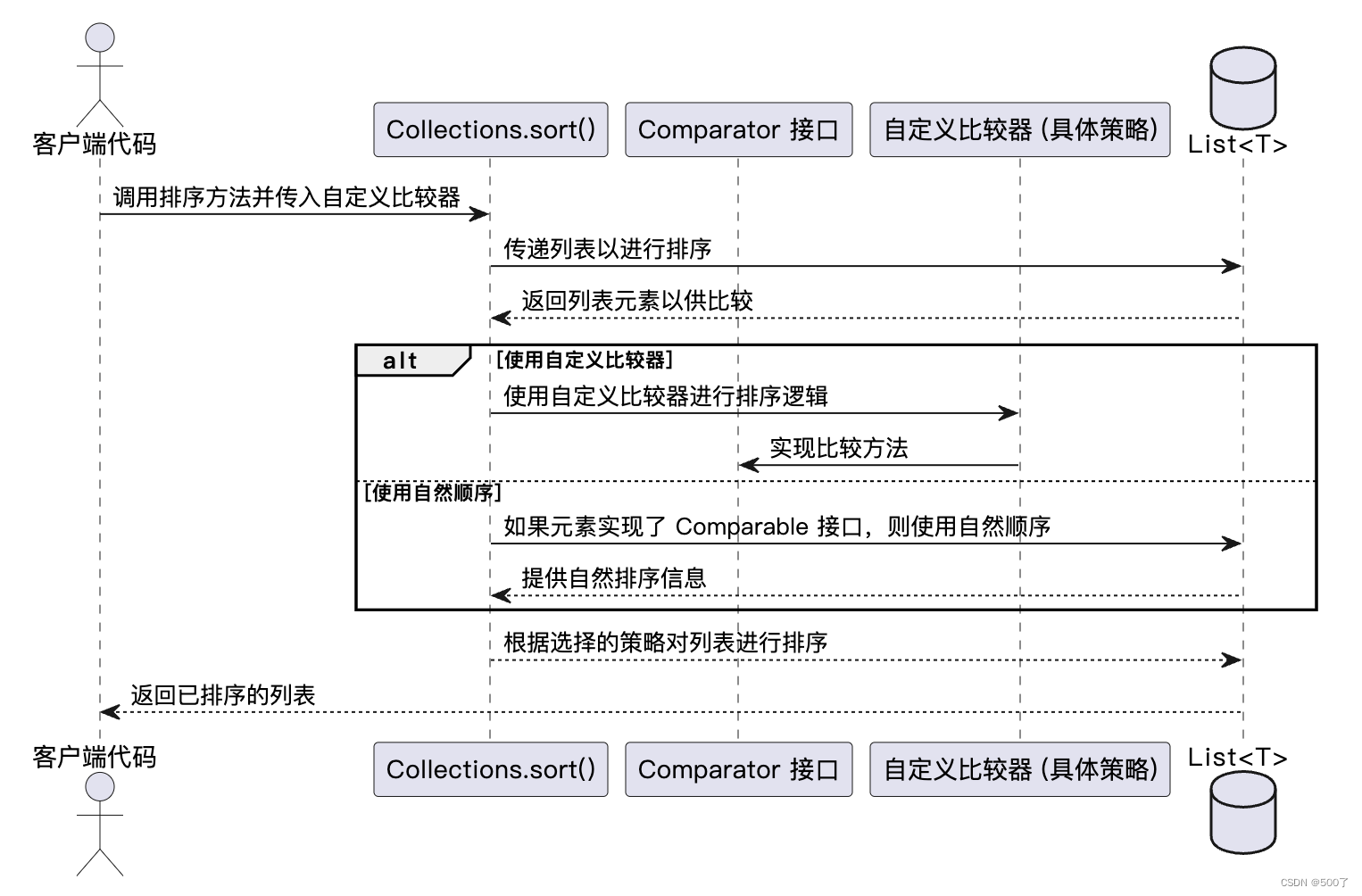
灵活应对:策略模式在软件设计中的应用
策略模式是一种行为型设计模式,它允许定义一系列算法,并将每个算法封装起来,使它们可以互换使用。策略模式让算法的变化独立于使用算法的客户端,使得在不修改原有代码的情况下切换或扩展新的算法成为可能。 使用策略模式的场景包…...
eosio.token 智能合约介绍
一、目的 eosio.token系统合约定义了允许用户为基于EOSIO的区块链创建、发行和管理代币的结构和操作,它演示了一种实现允许创建和管理代币的智能合约的方法。本文详细介绍了eosio.token系统合约并在本地测试链上实际发行了代币进行演示,适用于EOS智能合…...

3D 转换
1,3D的特点: 近小远大 物体后面遮挡不可见 2,3D移动 translate3d 3D移动在2D移动的基础上多加了一个可以移动的方向,就是z轴方向 transform:translateX(100px):仅仅是在x轴上移动…...

AI智能语音机器人安装方法
销售型的企业,基本靠电话营销拓客来实现效益的最大化。因为电销人员离职率高,且需求量大,需要接连不断的招人来实现业绩目标,电话机器人,贴牌招商,复制多个账户 这些都意味的企业的投入成本越来越大,博主从事多年AI技术…...

Python 潮流周刊#38:Django + Next.js 构建全栈项目
△△请给“Python猫”加星标 ,以免错过文章推送 你好,我是猫哥。这里每周分享优质的 Python、AI 及通用技术内容,大部分为英文。本周刊开源,欢迎投稿[1]。另有电报频道[2]作为副刊,补充发布更加丰富的资讯,…...
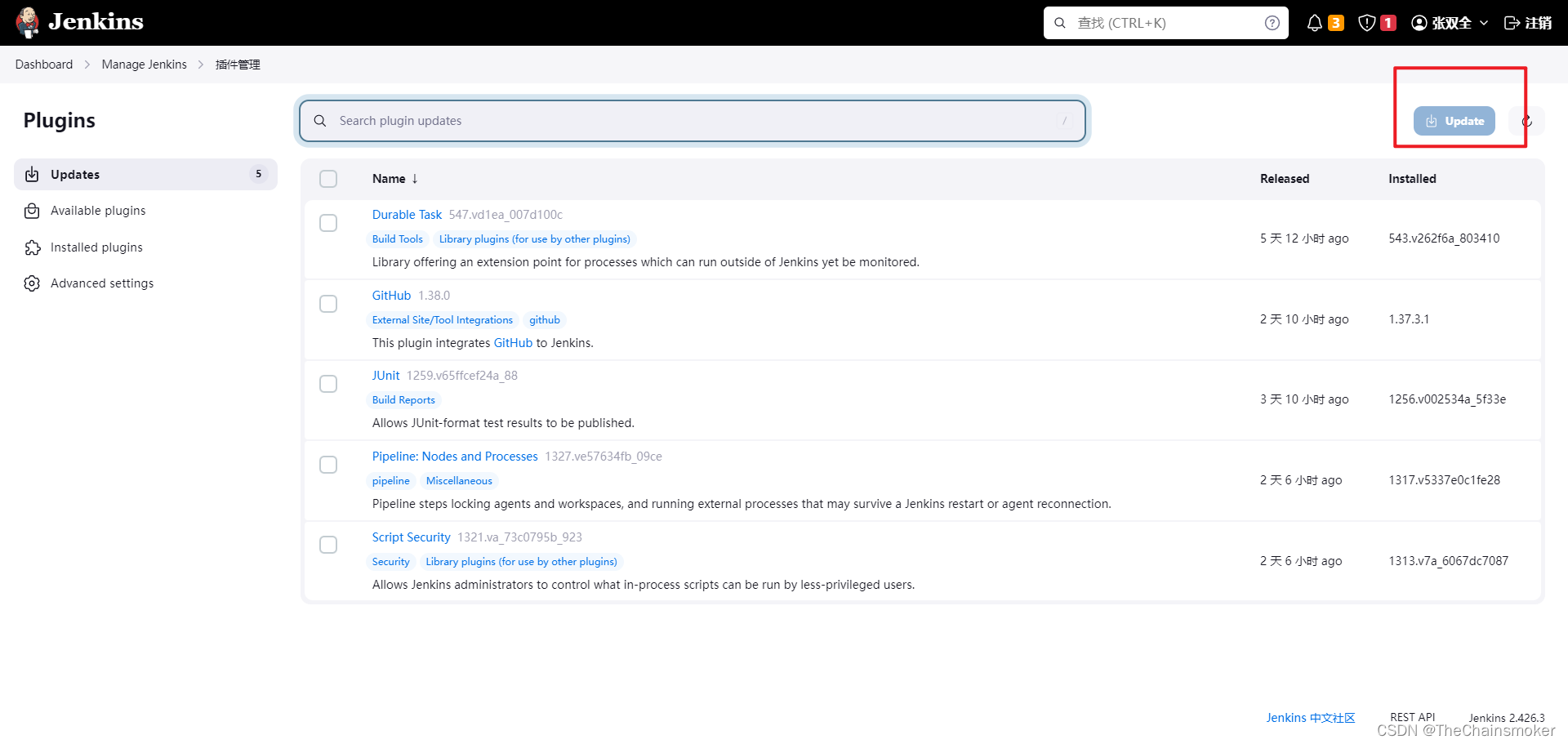
Jenkins升级后,构建任务配置界面重复错位
最近我把公司的Jenkins服务升级到了最新版本,升级完成后,点了一下构建任务,发现能够构建成功,就以为顺利完成升级了,下班走了,结果第二天,进入构建任务配置界面发现,界面一团乱麻&am…...

css实现圆环展示百分比,根据值动态展示所占比例
代码如下 <view class""><view class"circle-chart"><view v-if"!!num" class"pie-item" :style"{background: conic-gradient(var(--one-color) 0%,#E9E6F1 ${num}%),}"></view><view v-else …...

day52 ResNet18 CBAM
在深度学习的旅程中,我们不断探索如何提升模型的性能。今天,我将分享我在 ResNet18 模型中插入 CBAM(Convolutional Block Attention Module)模块,并采用分阶段微调策略的实践过程。通过这个过程,我不仅提升…...

遍历 Map 类型集合的方法汇总
1 方法一 先用方法 keySet() 获取集合中的所有键。再通过 gey(key) 方法用对应键获取值 import java.util.HashMap; import java.util.Set;public class Test {public static void main(String[] args) {HashMap hashMap new HashMap();hashMap.put("语文",99);has…...

多模态商品数据接口:融合图像、语音与文字的下一代商品详情体验
一、多模态商品数据接口的技术架构 (一)多模态数据融合引擎 跨模态语义对齐 通过Transformer架构实现图像、语音、文字的语义关联。例如,当用户上传一张“蓝色连衣裙”的图片时,接口可自动提取图像中的颜色(RGB值&…...

Qt Http Server模块功能及架构
Qt Http Server 是 Qt 6.0 中引入的一个新模块,它提供了一个轻量级的 HTTP 服务器实现,主要用于构建基于 HTTP 的应用程序和服务。 功能介绍: 主要功能 HTTP服务器功能: 支持 HTTP/1.1 协议 简单的请求/响应处理模型 支持 GET…...
:爬虫完整流程)
Python爬虫(二):爬虫完整流程
爬虫完整流程详解(7大核心步骤实战技巧) 一、爬虫完整工作流程 以下是爬虫开发的完整流程,我将结合具体技术点和实战经验展开说明: 1. 目标分析与前期准备 网站技术分析: 使用浏览器开发者工具(F12&…...

Maven 概述、安装、配置、仓库、私服详解
目录 1、Maven 概述 1.1 Maven 的定义 1.2 Maven 解决的问题 1.3 Maven 的核心特性与优势 2、Maven 安装 2.1 下载 Maven 2.2 安装配置 Maven 2.3 测试安装 2.4 修改 Maven 本地仓库的默认路径 3、Maven 配置 3.1 配置本地仓库 3.2 配置 JDK 3.3 IDEA 配置本地 Ma…...

DeepSeek 技术赋能无人农场协同作业:用 AI 重构农田管理 “神经网”
目录 一、引言二、DeepSeek 技术大揭秘2.1 核心架构解析2.2 关键技术剖析 三、智能农业无人农场协同作业现状3.1 发展现状概述3.2 协同作业模式介绍 四、DeepSeek 的 “农场奇妙游”4.1 数据处理与分析4.2 作物生长监测与预测4.3 病虫害防治4.4 农机协同作业调度 五、实际案例大…...

关键领域软件测试的突围之路:如何破解安全与效率的平衡难题
在数字化浪潮席卷全球的今天,软件系统已成为国家关键领域的核心战斗力。不同于普通商业软件,这些承载着国家安全使命的软件系统面临着前所未有的质量挑战——如何在确保绝对安全的前提下,实现高效测试与快速迭代?这一命题正考验着…...

Python 包管理器 uv 介绍
Python 包管理器 uv 全面介绍 uv 是由 Astral(热门工具 Ruff 的开发者)推出的下一代高性能 Python 包管理器和构建工具,用 Rust 编写。它旨在解决传统工具(如 pip、virtualenv、pip-tools)的性能瓶颈,同时…...
