韦达定理用处多
文章目录
- 前言
- 一、一元二次方程中根和系数之间的关系
- 二、韦达定理的数学推导和作用
- 1. 韦达定理的数学推导
- 2. 韦达定理的作用
- 三、韦达定理的应用举例
- 1. 解题示例1
- 2. 解题示例2
- 3. 解题示例3
- 4. 解题示例4
- 5. 解题示例5
- 6. 解题示例6
- 7. 解题示例7
- 总结
前言
韦达定理说明了一元n次方程中根和系数之间的关系。法国数学家韦达(F. Vieta,1540—1603)最早发现代数方程的根与系数之间有这种关系,因此,人们把这个关系称为韦达定理。有趣的是,韦达在16世纪就得出这个定理,证明这个定理要依靠代数基本定理,而代数基本定理却是在1799年才由高斯作出第一个实质性的论证。 韦达定理在方程论中有着广泛的应用。
一、一元二次方程中根和系数之间的关系
韦达定理指出了一元n次方程中根和系数之间的关系。
这里只谈一元二次方程中根和系数之间的关系。
对于一元二次方程
a x 2 + b x + c = 0 ( a ≠ 0 且△ = b 2 − 4 a c > 0 ) ax^2+bx+c=0 \space (a≠0 且△=b^2-4ac>0) ax2+bx+c=0 (a=0且△=b2−4ac>0)的两个根为 x 1 , x 2 x_1,x_2 x1,x2 有
x 1 + x 2 = − b a x_1+x_2= - \frac b a x1+x2=−ab
x 1 ⋅ x 2 = c a x_1·x_2= \frac c a x1⋅x2=ac
1 x 1 + 1 x 2 = x 1 + x 2 x 1 ⋅ x 2 \frac {1} {x_1} + \frac{1} {x_2} = \frac {x_1+x_2}{x_1·x_2} x11+x21=x1⋅x2x1+x2
二、韦达定理的数学推导和作用
1. 韦达定理的数学推导
由一元二次方程求根公式知:
x 1 , 2 = − b ± b 2 − 4 a c 2 a x_{1,2} = \frac {-b \pm \sqrt {b^2 - 4ac}} {2a} x1,2=2a−b±b2−4ac
则有:
x 1 + x 2 = − b + b 2 − 4 a c 2 a + − b − b 2 − 4 a c 2 a = − b a x_1 + x_2 = \frac {-b + \sqrt {b^2 - 4ac}} {2a} + \frac {-b - \sqrt {b^2 - 4ac}} {2a} = - \frac {b} {a} x1+x2=2a−b+b2−4ac+2a−b−b2−4ac=−ab
x 1 ⋅ x 2 = − b + b 2 − 4 a c 2 a × − b − b 2 − 4 a c 2 a = c a x_1 \cdot x_2 = \frac {-b + \sqrt {b^2 - 4ac}} {2a} \times \frac {-b - \sqrt {b^2 - 4ac}} {2a} = \frac {c} {a} x1⋅x2=2a−b+b2−4ac×2a−b−b2−4ac=ac
2. 韦达定理的作用
不论是解方程,还是研究方程的性质,韦达定理都很有用。
一般来说,韦达定理主要有以下四个方面的用途。
(1)利用韦达定理可以观察出一些一元二次方程的根;
(2)已知方程的两根之间的某种关系,可以求出方程的系数来;
(3)已知二次方程,求它的两个根的齐次幂的和;
(4)已知二次方程,求作一个新的二次方程,使得两个方程的根满足某种关系。
三、韦达定理的应用举例
1. 解题示例1
对于方程
x 2 − ( m − 1 ) x + m − 7 = 0 x^2 - (m-1)x + m-7 = 0 x2−(m−1)x+m−7=0
已知下列条件之一,求m的值。
(1)有一个根为0;
(2)两根互为倒数;
(3)两根互为相反数。
解:
(1)已知“有一个根为0”,不妨设 x 1 = 0 x_1=0 x1=0。由韦达定理可知
x 1 ⋅ x 2 = m − 7 x_1 \cdot x_2 = m-7 x1⋅x2=m−7
∵ x 1 = 0 \because x_1=0 ∵x1=0
∴ m − 7 = 0 , m = 7 \therefore m-7=0, m=7 ∴m−7=0,m=7
(2)已知“两根互为倒数”,必有 x 1 = 1 x 2 x_1= \frac {1} {x_2} x1=x21。由韦达定理可知
x 1 ⋅ x 2 = m − 7 x_1 \cdot x_2 = m-7 x1⋅x2=m−7
∵ x 1 ⋅ x 2 = x 1 ⋅ 1 x 1 = 1 \because x_1 \cdot x_2 = x_1 \cdot \frac {1} {x_1} = 1 ∵x1⋅x2=x1⋅x11=1
∴ m − 7 = 1 , m = 8 \therefore m-7=1, \space m=8 ∴m−7=1, m=8
(3)已知“两根互为相反数”,必有 x 1 = − x 2 x_1= -x_2 x1=−x2。由韦达定理可知
x 1 + x 2 = m − 1 x_1 + x_2 = m-1 x1+x2=m−1
∵ x 1 + x 2 = 0 \because x_1 + x_2 = 0 ∵x1+x2=0
∴ m − 1 = 0 , m = 1 \therefore m-1=0, \space m=1 ∴m−1=0, m=1
2. 解题示例2
已知方程 x 2 + 2 x − 18 = 0 x^2 + 2x -18 = 0 x2+2x−18=0的两根为 α , β \alpha, \beta α,β。
(1)写出以 2 α + 3 β 2\alpha+3\beta 2α+3β, 2 β + 3 α 2\beta+3\alpha 2β+3α为两根的方程;
(2)写出以 α + 2 β \alpha+\frac{2}{\beta} α+β2, β + 2 α \beta+\frac{2}{\alpha} β+α2为两根的方程。
解:
(1)由韦达定理得
α + β = − 2 , α ⋅ β = − 18 \alpha+\beta = -2,\space \alpha \cdot \beta = -18 α+β=−2, α⋅β=−18
∵ ( 2 α + 3 β ) + ( 2 β + 3 α ) = 5 ( α + β ) = 5 × ( − 2 ) = − 10 \because (2\alpha+3\beta) + (2\beta+3\alpha) = 5(\alpha+\beta) = 5 \times (-2) = -10 ∵(2α+3β)+(2β+3α)=5(α+β)=5×(−2)=−10
又 ∵ ( 2 α + 3 β ) ⋅ ( 2 β + 3 α ) \because (2\alpha+3\beta) \cdot (2\beta+3\alpha) ∵(2α+3β)⋅(2β+3α)
= 6 α 2 + 13 α β + 6 β 2 =6\alpha^2+13\alpha\beta+6\beta^2 =6α2+13αβ+6β2
= 6 ( α 2 + β 2 ) + 13 × ( − 18 ) =6(\alpha^2+\beta^2)+13\times(-18) =6(α2+β2)+13×(−18)
= 6 ( α 2 + β 2 ) − 234 =6(\alpha^2+\beta^2)-234 =6(α2+β2)−234
而 α 2 + β 2 = ( α + β ) 2 − 2 α β \alpha^2+\beta^2 = (\alpha+\beta)^2 - 2\alpha\beta α2+β2=(α+β)2−2αβ
= ( − 2 ) 2 − 2 × ( − 18 ) = 40 =(-2)^2 - 2\times(-18) = 40 =(−2)2−2×(−18)=40
∴ ( 2 α + 3 β ) ⋅ ( 2 β + 3 α ) \therefore (2\alpha+3\beta) \cdot (2\beta+3\alpha) ∴(2α+3β)⋅(2β+3α)
= 6 × 40 − 234 = 6 =6\times40-234 = 6 =6×40−234=6
∴ 所求方程为 x 2 + 10 x + 6 = 0 \therefore 所求方程为x^2 + 10x + 6 = 0 ∴所求方程为x2+10x+6=0
(1)由韦达定理得
( α + 2 β ) + ( β + 2 α ) (\alpha+\frac{2}{\beta}) + (\beta+\frac{2}{\alpha}) (α+β2)+(β+α2)
= α + β + 2 α + β α β = \alpha + \beta + 2 \frac {\alpha+\beta} {\alpha\beta} =α+β+2αβα+β
= − 2 + 2 × − 2 − 18 = − 16 9 = -2 + 2 \times \frac{-2}{-18} = - \frac {16} {9} =−2+2×−18−2=−916
又
( α + 2 β ) ⋅ ( β + 2 α ) (\alpha+\frac{2}{\beta}) \cdot (\beta+\frac{2}{\alpha}) (α+β2)⋅(β+α2)
= α β + 4 α β + 4 = − 18 + 4 − 18 + 4 = − 128 9 = \alpha \beta + \frac {4} { \alpha \beta} +4 = -18 + \frac {4} {-18} + 4 = - \frac {128} {9} =αβ+αβ4+4=−18+−184+4=−9128
∴ 所求方程为 9 x 2 + 16 x − 128 = 0 \therefore 所求方程为9x^2 + 16x - 128 = 0 ∴所求方程为9x2+16x−128=0
3. 解题示例3
已知方程 x 2 − x − 4 = 0 x^2 - x - 4 = 0 x2−x−4=0,不许解方程,求 x 1 2 + x 2 2 x_1^2 + x_2^2 x12+x22和 1 x 1 3 + 1 x 2 3 \frac {1} {x_1^3} + \frac {1} {x_2^3} x131+x231的值。 (1956年北京市中学生数学竞赛试题)
解:
由韦达定理可知
x 1 + x 2 = 1 , x 1 ⋅ x 2 = − 4 x_1 + x_2 = 1,x_1 · x_2 = -4 x1+x2=1,x1⋅x2=−4
x 1 2 + x 2 2 = ( x 1 + x 2 ) 2 − 2 x 1 x 2 = 1 2 − 2 × ( − 4 ) = 9 x_1^2 + x_2^2 = ( x_1 + x_2)^2 - 2 x_1 x_2 = 1^2 - 2 \times (-4) = 9 x12+x22=(x1+x2)2−2x1x2=12−2×(−4)=9
1 x 1 3 + 1 x 2 3 \frac {1} {x_1^3} + \frac {1} {x_2^3} x131+x231
= x 1 3 + x 2 3 x 1 3 ⋅ x 2 3 = ( x 1 + x 2 ) ( x 1 2 − x 1 x 2 + x 2 2 ) ( x 1 ⋅ x 2 ) 3 = \frac {x_1^3 + x_2^3} {x_1^3 \cdot x_2^3} = \frac {(x_1+x_2)( x_1^2 -x_1 x_2+ x_2^2)} {(x_1 \cdot x_2)^3} =x13⋅x23x13+x23=(x1⋅x2)3(x1+x2)(x12−x1x2+x22)
= ( x 1 + x 2 ) [ ( x 1 2 + x 2 2 ) − x 1 x 2 ] ( x 1 ⋅ x 2 ) 3 = \frac {(x_1+x_2)[( x_1^2 + x_2^2) - x_1 x_2]} {(x_1 \cdot x_2)^3} =(x1⋅x2)3(x1+x2)[(x12+x22)−x1x2]
1 × [ 9 − ( − 4 ) ] ( − 4 ) 3 = − 13 64 \frac {1 \times [9-(-4)]} {(-4)^3} = - \frac {13} {64} (−4)31×[9−(−4)]=−6413
4. 解题示例4
已知 p + q = 198 p+q=198 p+q=198,求方程 x 2 + p x + q = 0 x^2+px+q=0 x2+px+q=0的整数根. (94祖冲之杯数学邀请赛试题)
解:设方程的两整数根为 x 1 , x 2 x_1, x_2 x1,x2,不妨设 x 1 ≤ x 2 x_1≤x_2 x1≤x2. 由韦达定理,得
x 1 + x 2 = − p , x 1 ⋅ x 2 = q x_1+x_2=-p,x_1 \cdot x_2=q x1+x2=−p,x1⋅x2=q
于是 p + q = x 1 ⋅ x 2 − ( x 1 + x 2 ) = 198 p+q=x_1·x_2-(x_1+x_2)=198 p+q=x1⋅x2−(x1+x2)=198
即 x 1 ⋅ x 2 − x 1 − x 2 + 1 = 199 x_1·x_2-x_1-x_2+1=199 x1⋅x2−x1−x2+1=199
∴运用提取公因式法 ( x 1 − 1 ) ⋅ ( x 2 − 1 ) = 199 (x_1-1)·(x_2-1)=199 (x1−1)⋅(x2−1)=199
注意到 ( x 1 − 1 ) , ( x 2 − 1 ) (x_1-1), (x_2-1) (x1−1),(x2−1)均为整数,
解得 x 1 = 2 , x 2 = 200 ; x 1 = − 198 , x 2 = 0 x_1=2,x_2=200;x_1=-198,x_2=0 x1=2,x2=200;x1=−198,x2=0
5. 解题示例5
已知关于 x x x的方程 x 2 − ( 12 − m ) x + m − 1 = 0 x^2-(12-m)x+m-1=0 x2−(12−m)x+m−1=0的两个根都是正整数,求 m m m的值.
解:设方程的两个正整数根为 x 1 , x 2 x_1,x_2 x1,x2,且不妨设 x 1 ≤ x 2 x_1≤x_2 x1≤x2.由韦达定理得
x 1 + x 2 = 12 − m , x 1 ⋅ x 2 = m − 1 x_1+x_2=12-m,x_1 \cdot x_2=m-1 x1+x2=12−m,x1⋅x2=m−1
于是 x 1 ⋅ x 2 + x 1 + x 2 = 11 x_1 \cdot x_2 + x_1+x_2 = 11 x1⋅x2+x1+x2=11
即 ( x 1 + 1 ) ( x 2 + 1 ) = 12 (x_1+1)( x_2+1)=12 (x1+1)(x2+1)=12
∵ x 1 , x 2 x_1, x_2 x1,x2为正整数,
解得 x 1 = 1 , x 2 = 5 ; x 1 = 2 , x 2 = 3 x_1=1,x_2=5;x_1=2,x_2=3 x1=1,x2=5;x1=2,x2=3
故有 m = 6 ,或 m = 7. m=6,或m=7. m=6,或m=7.
6. 解题示例6
求实数 k k k,使得方程 k x 2 + ( k + 1 ) x + ( k − 1 ) = 0 kx^2+(k+1)x+(k-1)=0 kx2+(k+1)x+(k−1)=0的根都是整数.
解:若 k = 0 k=0 k=0,得 x = 1 x=1 x=1,即 k = 0 k=0 k=0符合要求.
若 k ≠ 0 k≠0 k=0,设二次方程的两个整数根为 x 1 , x 2 x_1,x_2 x1,x2,且 x 1 ≤ x 2 x_1≤x_2 x1≤x2,由韦达定理得
x 1 + x 2 = − k + 1 k , x 1 ⋅ x 2 = k − 1 k x_1+x_2 = - \frac {k+1} {k},x_1 \cdot x_2 = \frac {k-1} {k} x1+x2=−kk+1,x1⋅x2=kk−1
∴ x 1 ⋅ x 2 − x 1 − x 2 = k − 1 k − ( − k + 1 k ) = 2 ∴ x_1 \cdot x_2 - x_1 - x_2 = \frac {k-1} {k} - (- \frac {k+1} {k}) = 2 ∴x1⋅x2−x1−x2=kk−1−(−kk+1)=2
∴ ( x 1 − 1 ) ( x 2 − 1 ) = 3 ∴ (x_1-1)( x_2-1)=3 ∴(x1−1)(x2−1)=3
因为 x 1 − 1 , x 2 − 1 x_1 - 1, x_2 - 1 x1−1,x2−1均为整数,所以有
x 1 = 2 , x 2 = 4 ; x 1 = − 2 , x 2 = 0 x_1=2,x_2=4;x_1=-2,x_2=0 x1=2,x2=4;x1=−2,x2=0
所以 k = 1 ,或 k = − 1 7 k=1,或k=- \frac 1 7 k=1,或k=−71
7. 解题示例7
已知二次函数 y = − x 2 + p x + q y=-x^2+px+q y=−x2+px+q的图像与 x x x轴交于 ( α , 0 ) 、 ( β , 0 ) (α,0)、(β,0) (α,0)、(β,0)两点,且 α > 1 > β α>1>β α>1>β,求证: p + q > 1 p+q>1 p+q>1. (1997年四川省初中数学竞赛试题)
证明:由题意,可知方程 − x 2 + p x + q = 0 -x^2+px+q=0 −x2+px+q=0,即 x 2 − p x − q = 0 x^2-px-q=0 x2−px−q=0的两根为 α , β α,β α,β.
由韦达定理得 α + β = p , α β = − q α+β=p,αβ=-q α+β=p,αβ=−q
于是 p + q = α + β − α β = − ( α β − α − β + 1 ) + 1 p+q=α+β-αβ=-(αβ-α-β+1)+1 p+q=α+β−αβ=−(αβ−α−β+1)+1
因为 α > 1 > β α>1>β α>1>β,故
p + q = − ( α − 1 ) ( β − 1 ) + 1 > 1 p+q = -(α-1)(β-1)+1 > 1 p+q=−(α−1)(β−1)+1>1
总结
法国数学家韦达(F. Vieta,1540—1603)第一次有意识地使用系统的代数字母与符号,以辅音字母表示已知量,元音字母表示未知量,推进了方程论的发展,使代数成为一般类型的形式和方程的学问,因其抽象而应用更为广泛,被称为“代数符号之父”,在研究一元二次方程的解法时,他发现了一元二次方程的根与系数之间存在的特殊关系。 由于韦达最早发现代数方程的根与系数之间有这种关系,人们把这个关系称为韦达定理。
相关文章:

韦达定理用处多
文章目录 前言一、一元二次方程中根和系数之间的关系二、韦达定理的数学推导和作用1. 韦达定理的数学推导2. 韦达定理的作用 三、韦达定理的应用举例1. 解题示例12. 解题示例23. 解题示例34. 解题示例45. 解题示例56. 解题示例67. 解题示例7 总结 前言 韦达定理说明了一元n次方…...

Kotlin-类
构造函数 Java final File file new File("file.txt");Kotlin val file File("file.txt")类 Java public final class User { }Kotlin class User公开类 Java public class User { }Kotlin open class User属性类 Java final class User {pri…...

redis基本数据结构介绍
Redis(Remote Dictionary Server)是一个开源的高性能键值对数据库,它支持多种数据结构,包括字符串、哈希、列表、集合、有序集合等。这些数据结构为开发者提供了丰富的数据操作方式,使得Redis在缓存、消息队列、排行榜…...

云数据库RDS云监控
1. 什么是云数据库RDS?它有哪些特点? 云数据库RDS是一种在线关系型数据库服务,它具备的特点包括: 安全可靠:提供了容灾、备份、恢复等高可用性功能,确保数据的安全与可靠。弹性伸缩:用户可以根…...
全自动网页生成系统重构版源码
全自动网页生成系统重构版源码分享,所有模板经过精心审核与修改,完美兼容小屏手机大屏手机,以及各种平板端、电脑端和360浏览器、谷歌浏览器、火狐浏览器等等各大浏览器显示。 为用户使用方便考虑,全自动网页制作系统无需繁琐的注…...
Leetcode—33. 搜索旋转排序数组【中等】
2024每日刷题(110) Leetcode—33. 搜索旋转排序数组 实现代码 class Solution { public:int search(vector<int>& nums, int target) {int n nums.size();int l 0, r n - 1;while(l < r) {int m l (r - l) / 2;if(nums[m] target) …...
vulhub中Apache APISIX Dashboard API权限绕过导致RCE(CVE-2021-45232)
Apache APISIX是一个动态、实时、高性能API网关,而Apache APISIX Dashboard是一个配套的前端面板。 Apache APISIX Dashboard 2.10.1版本前存在两个API/apisix/admin/migrate/export和/apisix/admin/migrate/import,他们没有经过droplet框架的权限验证&…...

JavaSE习题 使用函数求最大值、求最大值方法的重载和求和方法的重载
目录 1 使用函数求最大值2 求最大值方法的重载3 求和方法的重载 1 使用函数求最大值 使用函数求最大值:创建方法求两个数的最大值max2,随后再写一个求3个数的最大值的函数max3。 要求: 在max3这个函数中,调用max2函数ÿ…...

英码科技携手昇腾共建算力底座:推出EA500I超强AI处理能力边缘计算盒子!
在数字经济浪潮中,算力已成为不可或缺的驱动力,为各行各业的数字化转型提供了强大的推动力。面对多元化和供需不平衡的挑战,需要实现从理论架构到软硬件实现的质的飞跃,以满足持续增长的算力需求,华为昇腾在这一方面展…...
蓝桥杯每日一题-----数位dp练习
题目 链接 参考代码 写了两个,一个是很久以前写的,一个是最近刚写的,很久以前写的时候还不会数位dp所以写了比较详细的注释,这两个代码主要是设置了不同的记忆数组,通过这两个代码可以理解记忆数组设置的灵活性。 im…...

JS(react)图片压缩+图片上传
上传dome var fileNodeTakeStock: any createRef();<inputref{fileNodeTakeStock}onChange{showPictureTakeStock}style{{ display: "none" }}id"fileInpBtn"type"file"accept"image/*" //限制上传格式multiple{false}capture&qu…...

WPF DispatcherTimer用法
System.Windows.Threading.DispatcherTimer 类主要用于WPF应用程序中进行周期性任务调度,并且保证这些任务在UI线程上执行。 这对于需要更新界面或与UI元素交互的定时操作非常有用,因为WPF的所有UI操作都必须在主线程(即Dispatcher线程&…...
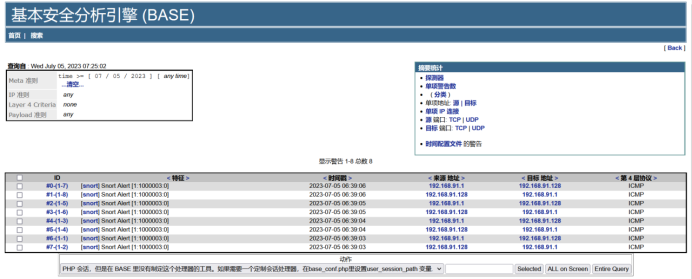
【网络安全实验】snort实现高级IDS
注:本实验分别使用kali和CentOS6.8进行测试,可惜的是使用kali进行实验过程中遇到了困难,未能完成完整实验,而使用CentOS6.8成功完成了完整实验。 实验中用到的软件: https://download.csdn.net/download/weixin_5255…...
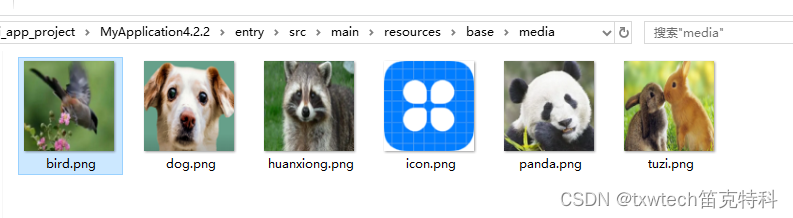
19.HarmonyOS App(JAVA)依赖布局DependentLayout使用方法
layout/ability_main.xml 显示位置不对:检查布局文件ohos:lef_of "id:tuzi",比如显示在兔子的左侧,这里就会显示不对。 需要id前没有$符号。改为: ohos:lef_of "$id:tuzi" <?xml version"1.0" encodi…...
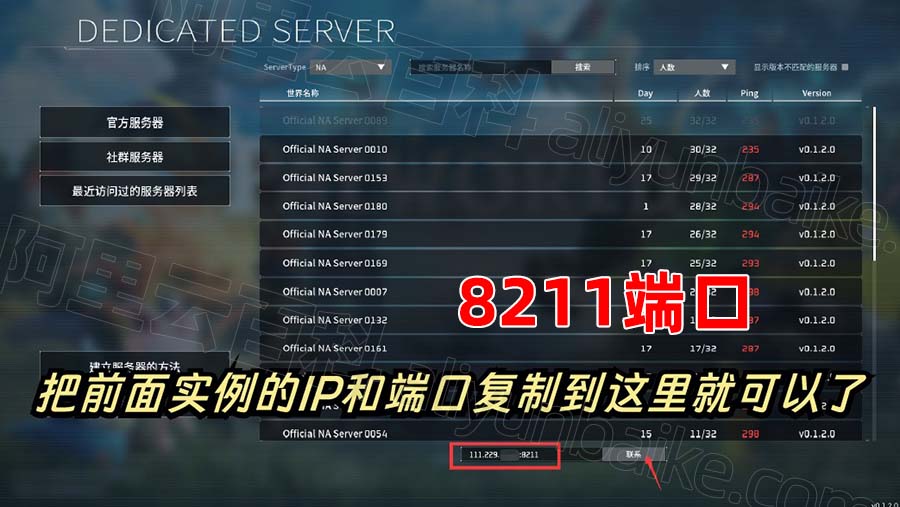
玩家笔记:幻兽帕鲁搭建服务器开服教程
玩转幻兽帕鲁服务器,阿里云推出新手0基础一键部署幻兽帕鲁服务器教程,傻瓜式一键部署,3分钟即可成功创建一台Palworld专属服务器,成本仅需26元,阿里云服务器网aliyunfuwuqi.com分享2024年新版基于阿里云搭建幻兽帕鲁服…...

Liunx基本指令
目录 1、ls 列出当前路径下的文件 2、pwd 打印当前工作目录 (print working directory) 3、cd 进入路径 4、mkdir 创建文件夹(make dirctory) 5、touch 创建文件 6、cp 复制(copy) 7、mv 移动/剪切、重命名 8、rm 删除 (remover) 9、vim 文本编辑器 10、cat 打开文件…...
面试题:Redis 分布式锁存在什么问题 ?如何解决 ?
文章目录 如何实现分布式锁2. Redis 分布式锁存在什么问题2.1 解决死锁问题2.2 解决锁误删问题 如何实现分布式锁 Redis 天生就可以作为一个分布式系统来使用,所以它实现的锁都是分布式锁。 Redis 可以通过 setnx(set if not exists)命令实…...
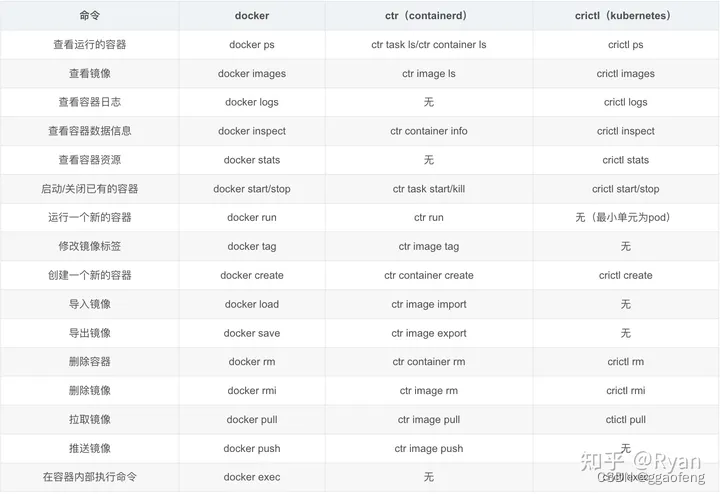
Container 命令ctr、crictl 命令
1、 Containerd和Docker的架构区别 Docker vs. Containerd: 2、ctr & crictl的区别 ctr是containerd的一个客户端工具 crictl 是 CRI 兼容的容器运行时命令行接口,可以使用它来检查和调试 Kubernetes 节点上的容器运行时和应用程序 crictl 则直接对…...

设计模式——七大原则
更多内容,前往 IT-BLOG 设计模式的目的是为了让程序,具有更好的代码重用性、可读性(编程规范性,便于后期维护和理解)、可扩展性(当需要增加新需求时,非常方便)、可靠性…...
笔记本电脑的WIFI模块,突然不显示了,网络也连接不上
问题复现: 早上,在更新完笔记本电脑的系统之后,连网之后,网络突然直接断开,一查看,WiFi模块居然不见了,开机重启也是如此,这种情况常常出现在更新系统之后,WiFi模块驱动就…...

SpringBoot-17-MyBatis动态SQL标签之常用标签
文章目录 1 代码1.1 实体User.java1.2 接口UserMapper.java1.3 映射UserMapper.xml1.3.1 标签if1.3.2 标签if和where1.3.3 标签choose和when和otherwise1.4 UserController.java2 常用动态SQL标签2.1 标签set2.1.1 UserMapper.java2.1.2 UserMapper.xml2.1.3 UserController.ja…...

在软件开发中正确使用MySQL日期时间类型的深度解析
在日常软件开发场景中,时间信息的存储是底层且核心的需求。从金融交易的精确记账时间、用户操作的行为日志,到供应链系统的物流节点时间戳,时间数据的准确性直接决定业务逻辑的可靠性。MySQL作为主流关系型数据库,其日期时间类型的…...

日语AI面试高效通关秘籍:专业解读与青柚面试智能助攻
在如今就业市场竞争日益激烈的背景下,越来越多的求职者将目光投向了日本及中日双语岗位。但是,一场日语面试往往让许多人感到步履维艰。你是否也曾因为面试官抛出的“刁钻问题”而心生畏惧?面对生疏的日语交流环境,即便提前恶补了…...

C# SqlSugar:依赖注入与仓储模式实践
C# SqlSugar:依赖注入与仓储模式实践 在 C# 的应用开发中,数据库操作是必不可少的环节。为了让数据访问层更加简洁、高效且易于维护,许多开发者会选择成熟的 ORM(对象关系映射)框架,SqlSugar 就是其中备受…...

3403. 从盒子中找出字典序最大的字符串 I
3403. 从盒子中找出字典序最大的字符串 I 题目链接:3403. 从盒子中找出字典序最大的字符串 I 代码如下: class Solution { public:string answerString(string word, int numFriends) {if (numFriends 1) {return word;}string res;for (int i 0;i &…...

【学习笔记】深入理解Java虚拟机学习笔记——第4章 虚拟机性能监控,故障处理工具
第2章 虚拟机性能监控,故障处理工具 4.1 概述 略 4.2 基础故障处理工具 4.2.1 jps:虚拟机进程状况工具 命令:jps [options] [hostid] 功能:本地虚拟机进程显示进程ID(与ps相同),可同时显示主类&#x…...

Unsafe Fileupload篇补充-木马的详细教程与木马分享(中国蚁剑方式)
在之前的皮卡丘靶场第九期Unsafe Fileupload篇中我们学习了木马的原理并且学了一个简单的木马文件 本期内容是为了更好的为大家解释木马(服务器方面的)的原理,连接,以及各种木马及连接工具的分享 文件木马:https://w…...

Xen Server服务器释放磁盘空间
disk.sh #!/bin/bashcd /run/sr-mount/e54f0646-ae11-0457-b64f-eba4673b824c # 全部虚拟机物理磁盘文件存储 a$(ls -l | awk {print $NF} | cut -d. -f1) # 使用中的虚拟机物理磁盘文件 b$(xe vm-disk-list --multiple | grep uuid | awk {print $NF})printf "%s\n"…...

Python基于历史模拟方法实现投资组合风险管理的VaR与ES模型项目实战
说明:这是一个机器学习实战项目(附带数据代码文档),如需数据代码文档可以直接到文章最后关注获取。 1.项目背景 在金融市场日益复杂和波动加剧的背景下,风险管理成为金融机构和个人投资者关注的核心议题之一。VaR&…...

AirSim/Cosys-AirSim 游戏开发(四)外部固定位置监控相机
这个博客介绍了如何通过 settings.json 文件添加一个无人机外的 固定位置监控相机,因为在使用过程中发现 Airsim 对外部监控相机的描述模糊,而 Cosys-Airsim 在官方文档中没有提供外部监控相机设置,最后在源码示例中找到了,所以感…...
