机器学习数学基础
机器学习基础
- 1、标量、向量、矩阵、张量
- 2、概率函数、概率分布、概率密度、分布函数
- 3、向量的线性相关性
- 4、最大似然估计
- 5、正态分布(高斯分布)
- 6、向量的外积(叉积)
- 7、向量的内积(点积)
- 8、超平面(Hyperplane)
- 9、广义线性模型(GLM)
- 10、伯努利分布与二项分布
- 11、凸函数
- 12、向量的相似性度量
1、标量、向量、矩阵、张量
标量、向量、矩阵和张量是线性代数中不同维度的数学对象,它们之间的区别在于维数和结构:
-
标量(Scalar):标量是一个数值,只有大小,没有方向。例如物理学中的时间、质量、温度等
-
向量(Vector):向量也称为欧几里得向量、几何向量、矢量,向量指既有大小又有方向的量。向量可以形象化地表示为带箭头的线段,箭头所指的方向代表向量的方向,线段的长度代表向量的大小。向量有四种表示方式:代数表示(字母加箭头)、几何表示(平行四边形法则)、坐标表示(
(x,y,z))和矩阵表示([x y z]T) -
矩阵(Matrix):矩阵是按照方阵排成m行n列的数值集合。简单来说,矩阵是一个二维数组,由行和列组成,每行和每列都是一个向量。矩阵中的每个元素都有自己的行索引和列索引,它可以用来表示线性变换、方程组或数据表
-
张量(Tensor):张量源于力学,张量是多维数组,目的是把向量、矩阵推向更高的维度。张量是一种泛化的多维数组概念,它可以是任何维度(秩)的,例如向量(矢量)是一阶张量,矩阵是二阶张量,高于二维的称为三阶张量、四阶张量等
总的来说,标量是最简单的数据形式,而向量、矩阵和更高维度的张量则是复杂度逐渐增加的多维数据结构,它们在现代科学和技术的许多领域中都扮演着重要角色
2、概率函数、概率分布、概率密度、分布函数
研究一个随机变量,不只是要看它能取哪些值,更重要的是它取各种值的概率如何!概率函数、概率分布、概率密度、分布函数,都是在描述概率
1)概率函数
概率函数使用函数的形式来表达概率 P i = P ( X = x i ) ( i = 1 , 2 , 3 , . . . ) P_i=P(X=x_i) \quad (i=1,2,3,...) Pi=P(X=xi)(i=1,2,3,...)
例如, P ( X P(X P(X= 1 ) = 1 / 6 1)=1/6 1)=1/6,这个概率函数表示当随机变量取值为1的概率为1/6。概率函数一次只能表示一个随机变量取值的概率
2)概率分布
概率分布是离散型随机变量和每个随机变量对应的概率:
| X | x 1 x_1 x1 | x 2 x_2 x2 | x 3 x_3 x3 | … | x n x_n xn |
|---|---|---|---|---|---|
| P i P_i Pi | P 1 P_1 P1 | P 2 P_2 P2 | P 3 P_3 P3 | … | P n P_n Pn |
这样的列表被叫做离散型随机变量的概率分布。具体就是离散型随机变量的值与这个取值的概率分布列表
对于连续型随机变量,概率分布被叫作概率密度
3)分布函数
对于离散型随机变量,分布函数称为概率分布函数,是指将某一点的概率与该点前面所有概率的累加,又称累积概率函数 F ( X ) = P ( X ≤ x i ) = ∑ 1 i P i F(X)=P(X≤x_i)=\sum_1^iP_i F(X)=P(X≤xi)=1∑iPi
分布函数是一个永不递减的函数,最右边即为最大值1,最左边为最小值0
对于连续型随机变量,分布函数称为概率密度函数,它就是概率密度从负无穷到当前随机变量值的定积分(面积)
F ( X ) = ∫ − ∞ X f ( x ) d x F(X)=\int_{-\infty}^Xf(x)dx F(X)=∫−∞Xf(x)dx

如图所示,左图表示 F ( x ) F(x) F(x)是连续型随机变量的概率密度,右图表示 f ( x ) f(x) f(x)是连续型随机变量的概率密度函数,它们之间的关系是:概率密度函数是概率密度的导函数
需要注意的是,概率密度函数在某点取值的几何意义表示概率密度函数在该点的变化率(导数),而不是概率值
3、向量的线性相关性
所有分量为实数的n维向量构成的集合, 称为一个n维向量空间,向量空间又称线性空间
对于n维向量 a 1 , a 2 , . . . a m a_1,a_2,...a_m a1,a2,...am,如果存在不全为0的数使得
k 1 a 1 + k 2 a 2 + . . . + k m a m = 0 k_1a_1+k_2a_2+...+k_ma_m=0 k1a1+k2a2+...+kmam=0
则称向量组 a 1 , a 2 , . . . a m a_1,a_2,...a_m a1,a2,...am是线性相关的,否则,称向量组 a 1 , a 2 , . . . a m a_1,a_2,...a_m a1,a2,...am线性无关
例如,对于向量 a 1 , a 2 , a 3 a_1,a_2,a_3 a1,a2,a3,若它们之间满足
a ⃗ 3 = − 1 2 a ⃗ 1 + 2 3 a ⃗ 2 \vec a_3 = -\frac{1}{2}\vec a_1+\frac{2}{3}\vec a_2 a3=−21a1+32a2
即向量 a 3 a_3 a3可以用向量 a 1 a_1 a1和 a 2 a_2 a2线性表示,说明 a 1 , a 2 , a 3 a_1,a_2,a_3 a1,a2,a3这三个向量是线性相关的
4、最大似然估计
最大似然估计的原理详解及推导见文章:传送门
5、正态分布(高斯分布)
正态分布(高斯分布)的介绍详见文章:传送门
6、向量的外积(叉积)
向量的叉乘(叉积),也叫向量的外积、向量积。在二维空间中,对于两个向量 a ⃗ = ( x 1 , y 1 ) \vec a=(x_1,y_1) a=(x1,y1)和 b ⃗ = ( x 2 , y 2 ) \vec b=(x_2,y_2) b=(x2,y2),定义它们的向量积为以下向量:
a ⃗ × b ⃗ = ∣ i ⃗ j ⃗ x 1 y 1 x 2 y 2 ∣ = x 1 y 2 i ⃗ − y 1 x 2 j ⃗ \vec a \times \vec b= \begin{vmatrix} \vec i&\vec j\\ x_1&y_1\\ x_2&y_2 \end{vmatrix} = x_1y_2 \vec i-y_1x_2 \vec j a×b= ix1x2jy1y2 =x1y2i−y1x2j
对于行列数相同的两个向量,叉积运算就是对这两个向量对角位相乘后求差的操作,叉积的结果是一个向量
在二维空间中,叉乘的几何意义是:叉乘的结果表示由向量 a ⃗ \vec a a和向量 b ⃗ \vec b b所构成的平行四边形的面积

即
a ⃗ × b ⃗ = ∣ a ⃗ ∣ ∣ b ⃗ ∣ sin θ \vec a \times \vec b=|\vec a||\vec b|\sin\theta a×b=∣a∣∣b∣sinθ
在三维空间中,对于两个向量 a ⃗ = ( x 1 , y 1 , z 1 ) \vec a=(x_1,y_1,z_1) a=(x1,y1,z1)和 b ⃗ = ( x 2 , y 2 , z 2 ) \vec b=(x_2,y_2,z_2) b=(x2,y2,z2),定义它们的向量积为以下向量:
a ⃗ × b ⃗ = ∣ i ⃗ j ⃗ k ⃗ x 1 y 1 z 1 x 2 y 2 z 2 ∣ = ( y 1 z 2 − y 2 z 1 ) i ⃗ − ( x 1 z 2 − x 2 z 1 ) j ⃗ + ( x 1 y 2 − x 2 y 1 ) k ⃗ \vec a \times \vec b= \begin{vmatrix} \vec i&\vec j&\vec k\\ x_1&y_1&z_1\\ x_2&y_2&z_2 \end{vmatrix} = (y_1z_2-y_2z_1)\vec i-(x_1z_2-x_2z_1)\vec j+(x_1y_2-x_2y_1)\vec k a×b=
相关文章:

机器学习数学基础
机器学习基础 1、标量、向量、矩阵、张量2、概率函数、概率分布、概率密度、分布函数3、向量的线性相关性4、最大似然估计5、正态分布(高斯分布)6、向量的外积(叉积)7、向量的内积(点积)8、超平面(Hyperplane)9、广义线性模型(GLM)10、伯努利分布与二项分布11、凸函数…...
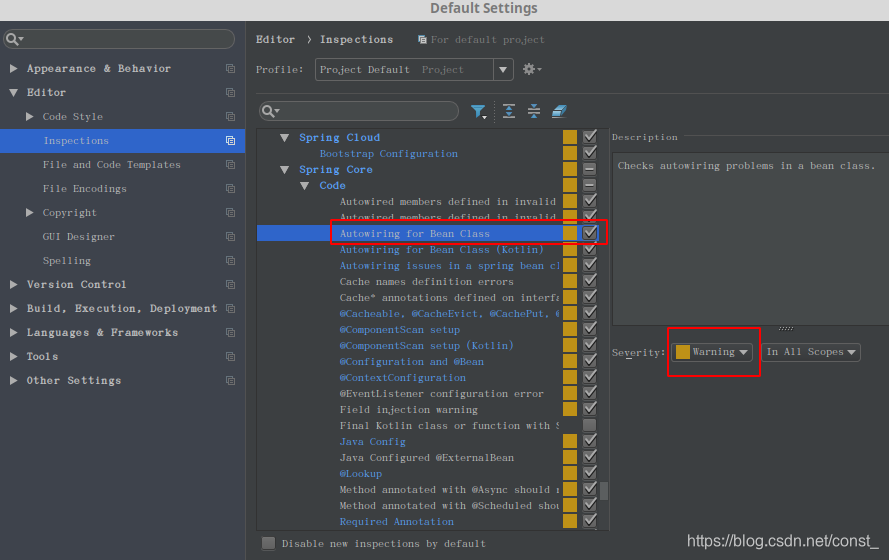
SpringBoot注解--04--01--注解@Mapper在IDEA中自动注入警告的解决方案
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 问题原因 解决方案方法1:为 Autowired 注解设置required false方法2:用 Resource 替换 Autowired方法3:在Mapper接口上加上Repo…...
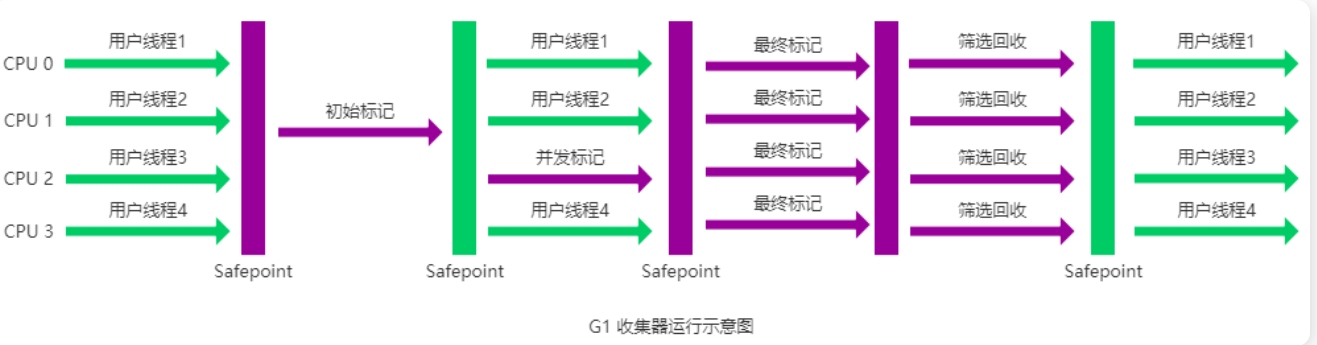
【Java八股面试系列】JVM-垃圾回收
目录 垃圾回收 堆空间的基本结构 内存分配和回收原则 分代收集机制 Minor GC 流程 空间分配担保 老年代 大对象直接进入老年代 长期存活的对象将进入老年代 GC的区域 对象存活判定算法 引用计数法 可达性分析算法 finalize() 字符串常量判活 类判活 垃圾回收算…...

Elasticsearch:集群故障排除和优化综合指南
Elasticsearch 是一个强大的搜索和分析引擎,是许多数据驱动应用程序和服务的核心。 它实时处理、分析和存储大量数据的能力使其成为当今快节奏的数字世界中不可或缺的工具。 然而,与任何复杂的系统一样,Elasticsearch 可能会遇到影响其性能和…...

初识C语言·编译与链接
1 翻译环境和运行环境 C语言标准ANSI C 实现C语言代码的时候 一般需要经过两种环境,一是翻译环境,二是运行环境,计算机能识别的是二进制的指令,人写完代码后通过翻译环境,使代码变成计算机能读懂的可执行的机器指令&a…...
)
堆与滑动窗口的结合(算法村第十六关黄金挑战)
滑动窗口最大值 239. 滑动窗口最大值 - 力扣(LeetCode) 给你一个整数数组 nums,有一个大小为 k 的滑动窗口从数组的最左侧移动到数组的最右侧。你只可以看到在滑动窗口内的 k 个数字。滑动窗口每次只向右移动一位。 返回 滑动窗口中的最大…...
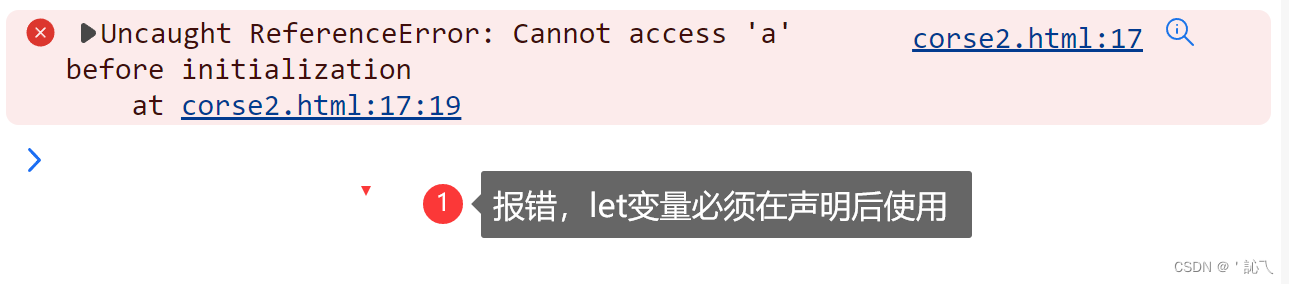
ES6-let
一、基本语法 ES6 中的 let 关键字用于声明变量,并且具有块级作用域。 - 语法:let 标识符;let 标识符初始值; - 规则:1.不能重复声明let不允许在相同作用域内重复声明同一个变量2.不存在变量提升在同一作用域内,必须先声明才能试…...
如何发布自己的npm包:
1.创建一个打包组件或者库: 安装weback: 打开项目: 创建webpack.config.js,创建src目录 打包好了后发现两个js文件都被压缩了,我们想开发使用未压缩,生产使用压缩文件。 erserPlugin:(推荐使用…...

JavaSE——流程控制-跳转关键字(break、continue),小案例(随机数、猜数字)
目录 跳转关键字 小案例(随机数) Random 猜数字 跳转关键字 break:跳出并结束当前所在循环的执行。continue:用于跳出当前循环的当次执行,直接进入循环的下一次执行。 注意事项: break:只能…...
Java HashSet 重写 equals() 和 hashCode() 对象去重
Ailt Insert 选择 equals() 和 hashCode() package com.zhong.collection.set;import java.util.HashSet; import java.util.Objects;public class HashSetDeduplication {public static void main(String[] args) {// HashSet 对象去重HashSet<Student> students new …...
Mac电脑到手后的配置
一、Homebrew 1、Homebrew安装 /bin/zsh -c "$(curl -fsSL https://gitee.com/cunkai/HomebrewCN/raw/master/Homebrew.sh)" 桌面的Old_Homebrew文件夹,没有你需要的可以删除。 2、Homebrew卸载 /bin/zsh -c "$(curl -fsSL https://gitee.com/c…...
Python中的while循环,知其然知其所以然
文章目录 while循环结构1.用循环打印1 ~ 100步骤解析2. 1 ~ 100的累加和3.死循环1. 用死循环的方法实现 1 ~ 100累加和 4. 单向循环(1)打印 一行十个小星星*(2)通过打印一个变量的形式,展现一行十个小星星(3)一行十个换色的星星 ★☆★☆★☆★☆★☆(4)用一个循环,打印十行十列…...

云瞻无代码开发:连接并集成电商平台、营销系统和CRM
无缝集成优势 云瞻信息已在电商领域取得杰出成就,其亮点在于其高效的社群运营和传统导购业务。云瞻的SAAS开放平台,一个连接和集成各种应用的工具,简化了传统的API开发流程。这赋能商家,即使没有专业的技术知识,也能够…...

LeetCode-第2469题=温度转换
1.题目描述 给你一个四舍五入到两位小数的非负浮点数 celsius 来表示温度,以 摄氏度(Celsius)为单位。 你需要将摄氏度转换为 开氏度(Kelvin)和 华氏度(Fahrenheit),并以数组 ans …...
docer compose部署simple-docker
简介 一个看似简陋但是功能足够用的docker管理工具 安装 创建目录 mkdir -p /opt/simple-docker cd /opt/simple-docker 创建并启动容器 编写docker-compose.yml文件,内容如下 version: 3 services: redis: image: redis:latest restart: always web: image: registry.cn-…...

Android Studio中打开文件管理器
文章目录 一、前言二、操作步骤 一、前言 在Android Studio中有时候需要查看手机的文件目录或者复制文件,但是有时候文件管理器找不到在哪,这里记录该操作流程 二、操作步骤 第一步: 第二步: 第三步:...

算法42:天际线问题(力扣218题)---线段树
218. 天际线问题 城市的 天际线 是从远处观看该城市中所有建筑物形成的轮廓的外部轮廓。给你所有建筑物的位置和高度,请返回 由这些建筑物形成的 天际线 。 每个建筑物的几何信息由数组 buildings 表示,其中三元组 buildings[i] [lefti, righti, heig…...
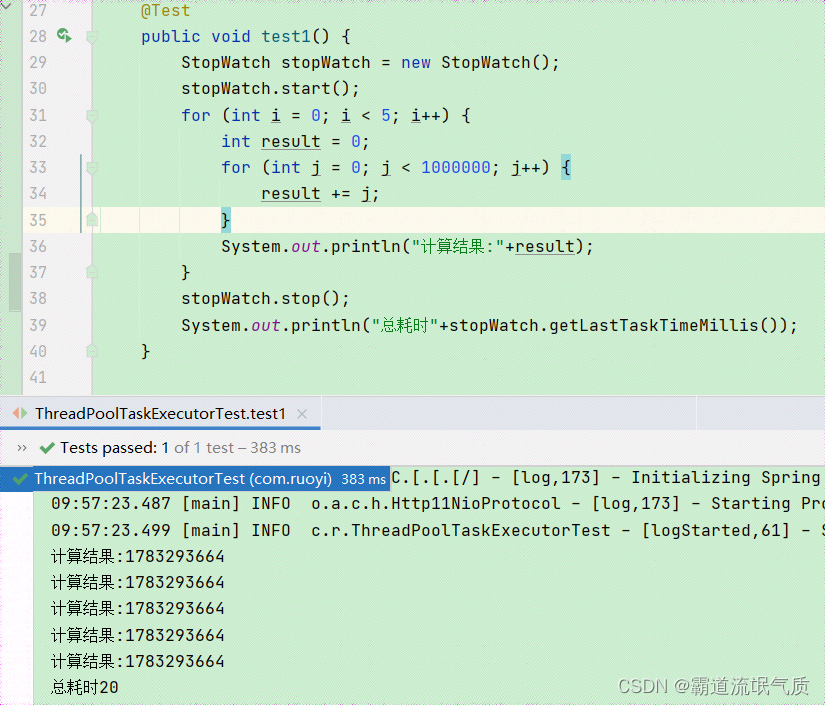
SpringBoot中使用Spring自带线程池ThreadPoolTaskExecutor与Java8CompletableFuture实现异步任务示例
场景 关于线程池的使用: Java中ExecutorService线程池的使用(Runnable和Callable多线程实现): Java中ExecutorService线程池的使用(Runnable和Callable多线程实现)_executorservice executorservice executors.newfix-CSDN博客 Java中创建线程的方式…...
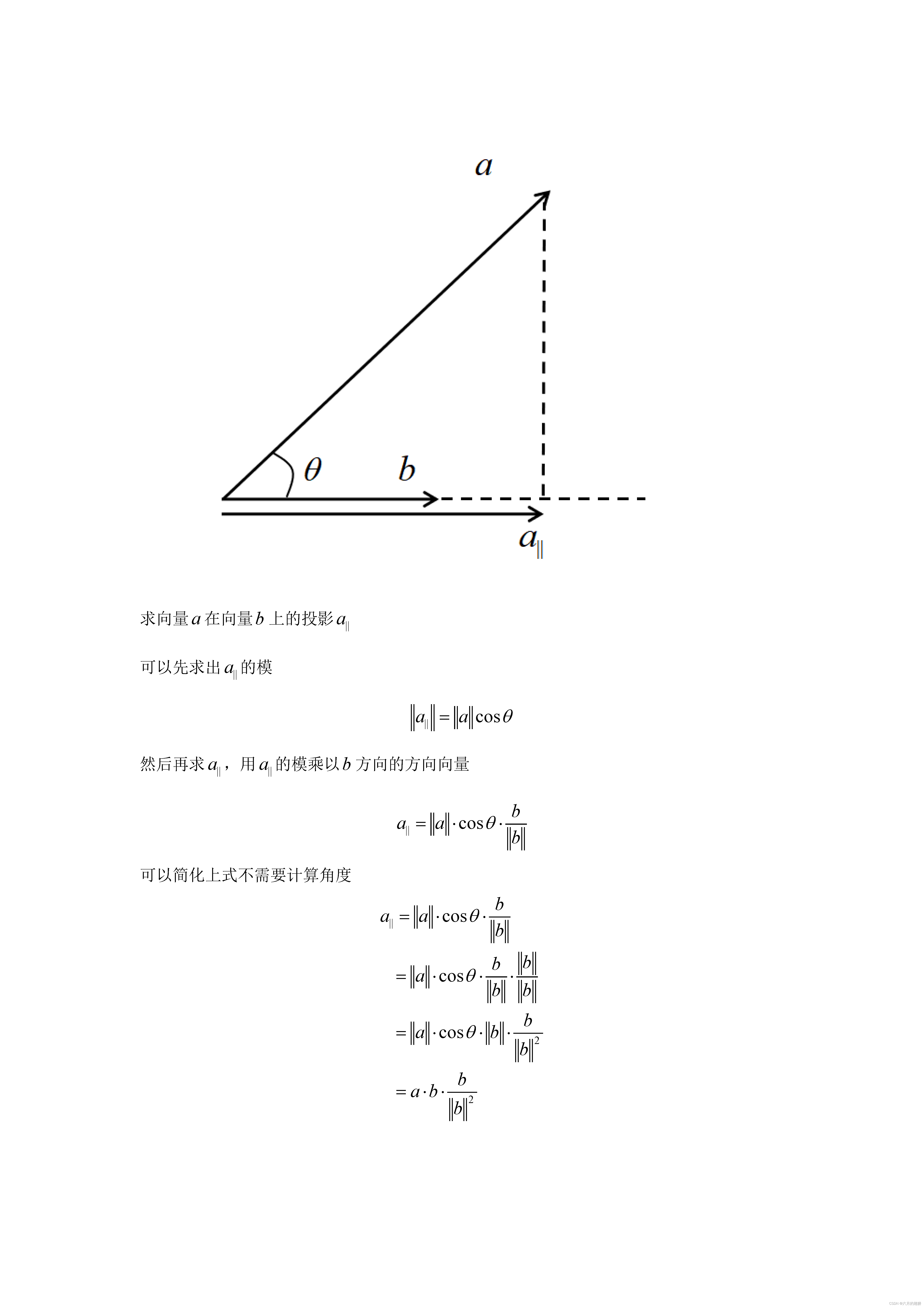
OpenCV/C++:点线面相关计算(二)
接续,继续更新 OpenCV/C:点线面相关计算_线面相交的点 代码计算-CSDN博客文章浏览阅读1.6k次,点赞2次,收藏12次。OpenCV处理点线面的常用操作_线面相交的点 代码计算https://blog.csdn.net/cd_yourheart/article/details/125626239 目录 1、…...
2024最新版鸿蒙HarmonyOS开发工具安装使用指南
2024最新版鸿蒙HarmonyOS开发工具安装使用指南 By JacksonML 0. 什么是鸿蒙Harmony OS? 华为鸿蒙系统(HUAWEI Harmony OS),是华为公司在2019年8月9日于东莞举行的华为开发者大会(HDC.2019)上正式发布的分…...

Unity3D中Gfx.WaitForPresent优化方案
前言 在Unity中,Gfx.WaitForPresent占用CPU过高通常表示主线程在等待GPU完成渲染(即CPU被阻塞),这表明存在GPU瓶颈或垂直同步/帧率设置问题。以下是系统的优化方案: 对惹,这里有一个游戏开发交流小组&…...

【android bluetooth 框架分析 04】【bt-framework 层详解 1】【BluetoothProperties介绍】
1. BluetoothProperties介绍 libsysprop/srcs/android/sysprop/BluetoothProperties.sysprop BluetoothProperties.sysprop 是 Android AOSP 中的一种 系统属性定义文件(System Property Definition File),用于声明和管理 Bluetooth 模块相…...

第一篇:Agent2Agent (A2A) 协议——协作式人工智能的黎明
AI 领域的快速发展正在催生一个新时代,智能代理(agents)不再是孤立的个体,而是能够像一个数字团队一样协作。然而,当前 AI 生态系统的碎片化阻碍了这一愿景的实现,导致了“AI 巴别塔问题”——不同代理之间…...

中医有效性探讨
文章目录 西医是如何发展到以生物化学为药理基础的现代医学?传统医学奠基期(远古 - 17 世纪)近代医学转型期(17 世纪 - 19 世纪末)现代医学成熟期(20世纪至今) 中医的源远流长和一脉相承远古至…...
:观察者模式)
JS设计模式(4):观察者模式
JS设计模式(4):观察者模式 一、引入 在开发中,我们经常会遇到这样的场景:一个对象的状态变化需要自动通知其他对象,比如: 电商平台中,商品库存变化时需要通知所有订阅该商品的用户;新闻网站中࿰…...

JVM虚拟机:内存结构、垃圾回收、性能优化
1、JVM虚拟机的简介 Java 虚拟机(Java Virtual Machine 简称:JVM)是运行所有 Java 程序的抽象计算机,是 Java 语言的运行环境,实现了 Java 程序的跨平台特性。JVM 屏蔽了与具体操作系统平台相关的信息,使得 Java 程序只需生成在 JVM 上运行的目标代码(字节码),就可以…...

MFC 抛体运动模拟:常见问题解决与界面美化
在 MFC 中开发抛体运动模拟程序时,我们常遇到 轨迹残留、无效刷新、视觉单调、物理逻辑瑕疵 等问题。本文将针对这些痛点,详细解析原因并提供解决方案,同时兼顾界面美化,让模拟效果更专业、更高效。 问题一:历史轨迹与小球残影残留 现象 小球运动后,历史位置的 “残影”…...
)
【LeetCode】3309. 连接二进制表示可形成的最大数值(递归|回溯|位运算)
LeetCode 3309. 连接二进制表示可形成的最大数值(中等) 题目描述解题思路Java代码 题目描述 题目链接:LeetCode 3309. 连接二进制表示可形成的最大数值(中等) 给你一个长度为 3 的整数数组 nums。 现以某种顺序 连接…...

Linux-进程间的通信
1、IPC: Inter Process Communication(进程间通信): 由于每个进程在操作系统中有独立的地址空间,它们不能像线程那样直接访问彼此的内存,所以必须通过某种方式进行通信。 常见的 IPC 方式包括&#…...

MySQL体系架构解析(三):MySQL目录与启动配置全解析
MySQL中的目录和文件 bin目录 在 MySQL 的安装目录下有一个特别重要的 bin 目录,这个目录下存放着许多可执行文件。与其他系统的可执行文件类似,这些可执行文件都是与服务器和客户端程序相关的。 启动MySQL服务器程序 在 UNIX 系统中,用…...
