《统计学习方法:李航》笔记 从原理到实现(基于python)-- 第6章 逻辑斯谛回归与最大熵模型(1)6.1 逻辑斯谛回归模型
文章目录
- 第6章 逻辑斯谛回归与最大熵模型
- 6.1 逻辑斯谛回归模型
- 6.1.1 逻辑斯谛分布
- 6.1.2 二项逻辑斯谛回归模型
- 6.1.3 模型参数估计
- 6.1.4 多项逻辑斯谛回归
《统计学习方法:李航》笔记 从原理到实现(基于python)-- 第3章 k邻近邻法
《统计学习方法:李航》笔记 从原理到实现(基于python)-- 第1章 统计学习方法概论
《统计学习方法:李航》笔记 从原理到实现(基于python)-- 第 2章感知机
《统计学习方法:李航》笔记 从原理到实现(基于python)-- 第3章 k邻近邻法
《统计学习方法:李航》笔记 从原理到实现(基于python)-- 第4章 朴素贝叶斯法
《统计学习方法:李航》笔记 从原理到实现(基于python)-- 第5章 决策树
我算是有点基础的(有过深度学习和机器学的项目经验),但也是半路出家,无论是学Python还是深度学习,都是从问题出发,边查边做,没有系统的学过相关的知识,这样的好处是入门快(如果想快速入门,大家也可以试试,直接上手项目,从小项目开始),但也存在一个严重的问题就是,很多东西一知半解,容易走进死胡同出不来(感觉有点像陷入局部最优解,找不到出路),所以打算系统的学习几本口碑比较不错的书籍。
书籍选择: 当然,机器学习相关的书籍有很多,很多英文版的神书,据说读英文版的书会更好,奈何英文不太好,比较难啃。国内也有很多书,周志华老师的“西瓜书”我也有了解过,看了前几章,个人感觉他肯能对初学者更友好一点,讲述的非常清楚,有很多描述性的内容。对比下来,更喜欢《统计学习方法》,毕竟能坚持看完才最重要。
笔记内容: 笔记内容尽量省去了公式推导的部分,一方面latex编辑太费时间了,另一方面,我觉得公式一定要自己推到一边才有用(最好是手写)。尽量保留所有标题,但内容会有删减,通过标黑和列表的形式突出重点内容,要特意说一下,标灰的部分大家最好读一下(这部分是我觉得比较繁琐,但又不想删掉的部分)。
代码实现: 最后是本章内容的实践,如果想要对应的.ipynb文件,可以留言
第6章 逻辑斯谛回归与最大熵模型
逻辑斯谛回归(logistic regression) 是统计学习中的经典分类方法。最大熵是概率模型学习的一个准则,将其推广到分类问题得到最大熵模型(maximum entropy model)。
逻辑斯谛回归模型与最大熵模型都属于对数线性模型。
6.1 逻辑斯谛回归模型
6.1.1 逻辑斯谛分布
首先介绍逻辑斯谛分布(logistic distribution)。

逻辑斯谛分布的密度函数 f ( x ) f(x) f(x)和分布函数 F ( x ) F(x) F(x)的图形如图6.1所示。分布函数属于逻辑斯谛函数,其图形是一条S形曲线(sigmoid curve)。该曲线以点 为中心对称,即满足:

曲线在中心附近增长速度较快,在两端增长速度较慢。形状参数 γ γ γ的值越小,曲线在中心附近增长得越快。
6.1.2 二项逻辑斯谛回归模型
二项逻辑斯谛回归模型(binomial logistic regression model)是一种分类模型,由条件概率分布 P ( Y ∣ X ) P(Y|X) P(Y∣X)表示,形式为参数化的逻辑斯谛分布。
这里,随机变量 X X X取值为实数,随机变量 Y Y Y取值为1或0。我们通过监督学习的方法来估计模型参数。

对于给定的输入实例 x x x,按照式(6.3)和式(6.4)可以求得 P ( Y = 1 ∣ x ) P(Y=1|x) P(Y=1∣x)和 P ( Y = 0 ∣ x ) P(Y=0|x) P(Y=0∣x)。
逻辑斯谛回归比较两个条件概率值的大小,将实例 x x x分到概率值较大的那一类。
有时为了方便,将权值向量和输入向量加以扩充,仍记作 w , x w,x w,x,即
- 权值向量: w = ( w ( 1 ) , w ( 2 ) , … , w ( n ) , b ) T w=(w^{(1)},w^{(2)}, …,w^{(n)},b)^T w=(w(1),w(2),…,w(n),b)T,
- 输入向量: x = ( x ( 1 ) , x ( 2 ) , … , x ( n ) , 1 ) T x=(x^{(1)},x^{(2)},…,x^{(n)},1)^T x=(x(1),x(2),…,x(n),1)T。
这时,逻辑斯谛回归模型如下:

逻辑斯谛回归模型的特点。
一个事件的几率(odds)是指该事件发生的概率与该事件不发生的概率的比值。
如果事件发生的概率是p,那么该事件的几率是 p 1 − p \frac{p}{1-p} 1−pp ,该事件的对数几率(log odds)或logit函数是
l o g i t ( p ) = l o g p 1 − p logit(p)=log\frac{p}{1-p} logit(p)=log1−pp
对逻辑斯谛回归而言,由式(6.5)与式(6.6)得
l o g P ( Y = 1 ∣ x ) 1 − P ( Y = 1 ∣ x ) = w ⋅ x log\frac{P(Y=1|x)}{1-P(Y=1|x)} = w\cdot x log1−P(Y=1∣x)P(Y=1∣x)=w⋅x
这就是说,在逻辑斯谛回归模型中,输出 Y = 1 Y=1 Y=1的对数几率是输入 x x x的线性函数。(或者说,输出 Y = 1 Y=1 Y=1的对数几率是由输入 x x x的线性函数表示的模型,即逻辑斯谛回归模型。)
换一个角度看,考虑对输入 x x x进行分类的线性函数 w ⋅ x w·x w⋅x,其值域为实数域。注意,这里 x ∊ R N + 1 x∊R^{N+1} x∊RN+1, w ∊ R N + 1 w∊R^{N+1} w∊RN+1。通过逻辑斯谛回归模型定义式(6.5)可以将线性函数 w ⋅ x w·x w⋅x转换为概率:
P ( Y = 1 ∣ x ) = e x p ( w ⋅ x ) 1 + e x p ( w ⋅ x ) P(Y=1|x)=\frac{exp(w \cdot x)}{1+exp(w \cdot x)} P(Y=1∣x)=1+exp(w⋅x)exp(w⋅x)
这时,
- 线性函数的值越接近正无穷,概率值就越接近1;
- 线性函数的值越接近负无穷,概率值就越接近0(如图6.1所示)。
这样的模型就是逻辑斯谛回归模型。
6.1.3 模型参数估计
逻辑斯谛回归模型学习时,对于给定的训练数据集 T = ( x 1 , y 1 ) , ( x 2 , y 2 ) , … , ( x N , y N ) T={(x_1,y_1),(x_2,y_2),…,(x_N,y_N)} T=(x1,y1),(x2,y2),…,(xN,yN),其中, x i ∊ R n x_i∊R^n xi∊Rn, y i ∊ 0 , 1 y_i∊{0,1} yi∊0,1,可以应用极大似然估计法估计模型参数,从而得到逻辑斯谛回归模型。
设:
P ( Y = 1 ∣ x ) = π ( x ) P(Y=1|x)=\pi(x) P(Y=1∣x)=π(x)
P ( Y = 0 ∣ x ) = 1 − π ( x ) P(Y=0|x)=1-\pi(x) P(Y=0∣x)=1−π(x)
似然函数为:
∏ i = 0 N [ π ( x i ) ] y i [ 1 − π ( x i ) ] 1 − y i ] \prod \limits_{i=0}^N[\pi(x_i)]^{y_i}[1-\pi(x_i)]^{1-y_i}] i=0∏N[π(xi)]yi[1−π(xi)]1−yi]
对数似然函数为:

对 L ( w ) L(w) L(w)求极大值,得到 w w w的估计值。
这样,问题就变成了以对数似然函数为目标函数的最优化问题。逻辑斯谛回归学习中通常采用的方法是梯度下降法及拟牛顿法。
假设 w w w的极大似然估计值是 ,那么学到的逻辑斯谛回归模型为
P ( Y = 1 ∣ x ) = e x p ( w ^ ⋅ x ) 1 + e x p ( w ^ ⋅ x ) P(Y=1|x)=\frac{exp(\hat{w} \cdot x)}{1+exp(\hat{w} \cdot x)} P(Y=1∣x)=1+exp(w^⋅x)exp(w^⋅x)
P ( Y = 0 ∣ x ) = 1 1 + e x p ( w ^ ⋅ x ) P(Y=0|x)=\frac{1}{1+exp(\hat{w} \cdot x)} P(Y=0∣x)=1+exp(w^⋅x)1
6.1.4 多项逻辑斯谛回归
上面介绍的逻辑斯谛回归模型是二项分类模型,用于二类分类。
可以将其推广为多项逻辑斯谛回归模型(multi-nominal logistic regression model),用于多类分类。
假设离散型随机变量Y的取值集合是 1 , 2 , … , K {1,2,…,K} 1,2,…,K,那么多项逻辑斯谛回归模型是

二项逻辑斯谛回归的参数估计法也可以推广到多项逻辑斯谛回归。
相关文章:

《统计学习方法:李航》笔记 从原理到实现(基于python)-- 第6章 逻辑斯谛回归与最大熵模型(1)6.1 逻辑斯谛回归模型
文章目录 第6章 逻辑斯谛回归与最大熵模型6.1 逻辑斯谛回归模型6.1.1 逻辑斯谛分布6.1.2 二项逻辑斯谛回归模型6.1.3 模型参数估计6.1.4 多项逻辑斯谛回归 《统计学习方法:李航》笔记 从原理到实现(基于python)-- 第3章 k邻近邻法 《统计学习…...
Go 中如何检查文件是否存在?可能产生竞态条件?
嗨,大家好!本文是系列文章 Go 技巧第十三篇,系列文章查看:Go 语言技巧。 Go 中如何检查文件是否存在呢? 如果你用的是 Python,可通过标准库中 os.path.exists 函数实现。遗憾的是,Go 标准库没有…...

红日靶场1搭建渗透
环境搭建 下载好镜像文件并解压,启动vmware 这里我用自己的win7 sp1虚拟机作为攻击机,设置为双网卡NAT,vm2 其中用ipconfig查看攻击机ip地址 设置win7 x64为双网卡,vm1,vm2 设置win08单网卡vm1,win2k3为单…...
ChatGPT之搭建API代理服务
简介 一行Docker命令部署的 OpenAI/GPT API代理,支持SSE流式返回、腾讯云函数 。 项目地址:https://github.com/easychen/openai-api-proxy 这个项目可以自行搭建 OpenAI API 代理服务器工具,该项目是代理的服务器端,不是客户端。…...
:基础大杂烩)
Kotlin手记(一):基础大杂烩
Kotlin简介 2011年7月,JetBrains推出Kotlin项目,这是一个面向JVM的新语言 2012年2月,JetBrains以Apache 2许可证开源此项目。 2016年2月15日,Kotlin v1.0发布,这被认为是第一个官方稳定版本。 在Google I/O 2017中&am…...

redis源码之:集群创建与节点通信(2)
在上一篇redis源码之:集群创建与节点通信(1)我们可知,在集群中,cluster节点之间,通过meet将对方加入到本方的cluster->nodes列表中,并在后续过程中,不断通过clusterSendPing发送p…...
)
2024.2.5 寒假训练记录(19)
文章目录 牛客 寒假集训2A Tokitsukaze and Bracelet牛客 寒假集训2B Tokitsukaze and Cats牛客 寒假集训2D Tokitsukaze and Slash Draw牛客 寒假集训2E Tokitsukaze and Eliminate (easy)牛客 寒假集训2F Tokitsukaze and Eliminate (hard)牛客 寒假集训2I Tokitsukaze and S…...
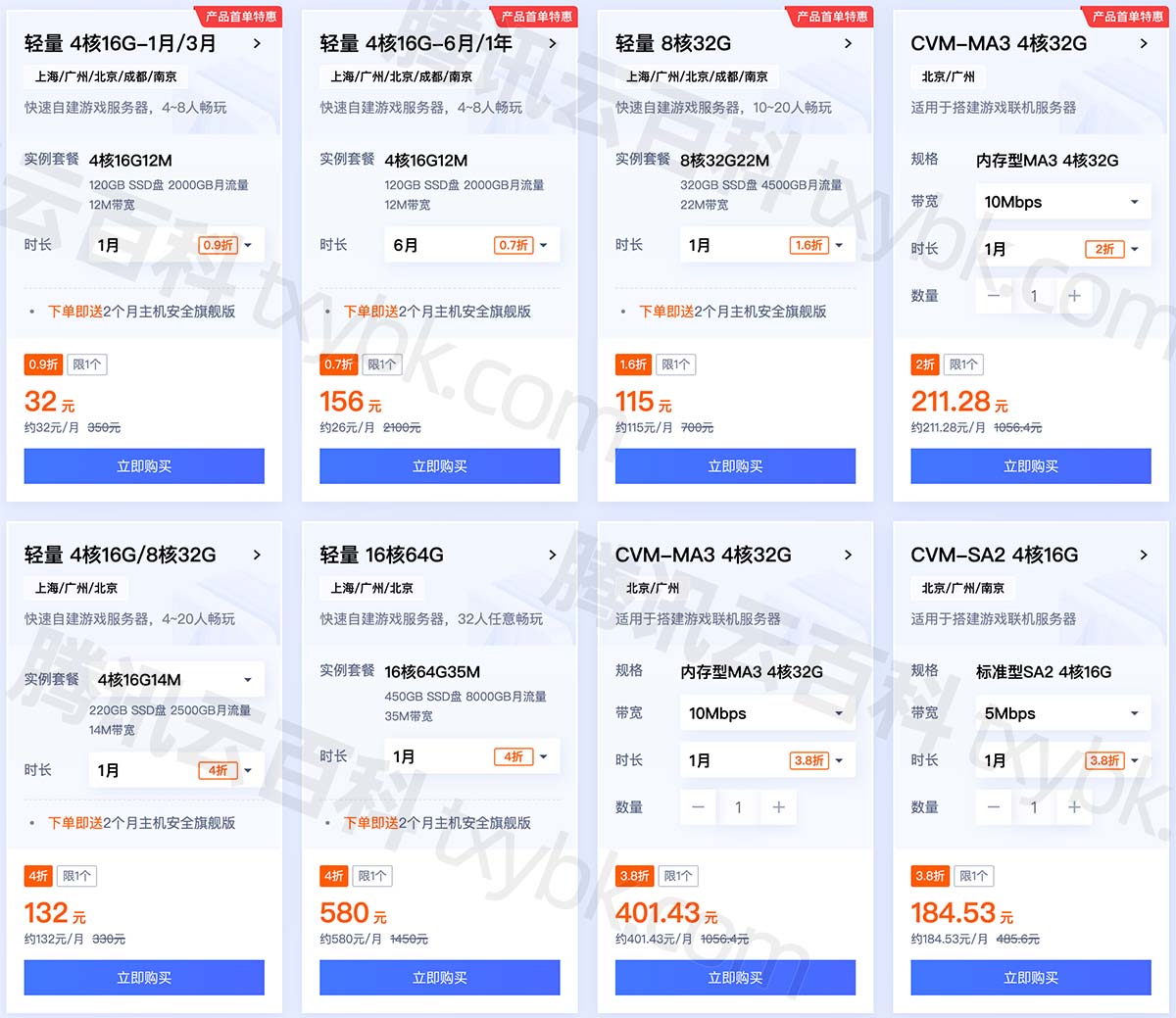
游戏服务器租赁多少钱一台?26元,服不服?
游戏服务器租用多少钱一年?1个月游戏服务器费用多少?阿里云游戏服务器26元1个月、腾讯云游戏服务器32元,游戏服务器配置从4核16G、4核32G、8核32G、16核64G等配置可选,可以选择轻量应用服务器和云服务器,阿腾云atengyu…...

wpf 引入本项目的图片以及引入其他项目的图像资源区别及使用方法
在WPF项目中引入本项目的图片和引入其他项目的图像资源,两者的主要区别在于资源的位置以及如何通过URI引用它们。以下是详细说明及使用方法: 一、引入本项目的图片资源: 将图片文件(如PNG, JPG等)放入你的WPF项目…...

jsp页面,让alert弹出信息换行显示
第一种方式:后端拼接上换行符前端显示 1,java后端将信息封装成字符串时,在需要换行的地方拼接上一个换行符, 显示在HTML中的换行,通常需要用<br>标签替代\n,如下: String javaString &…...
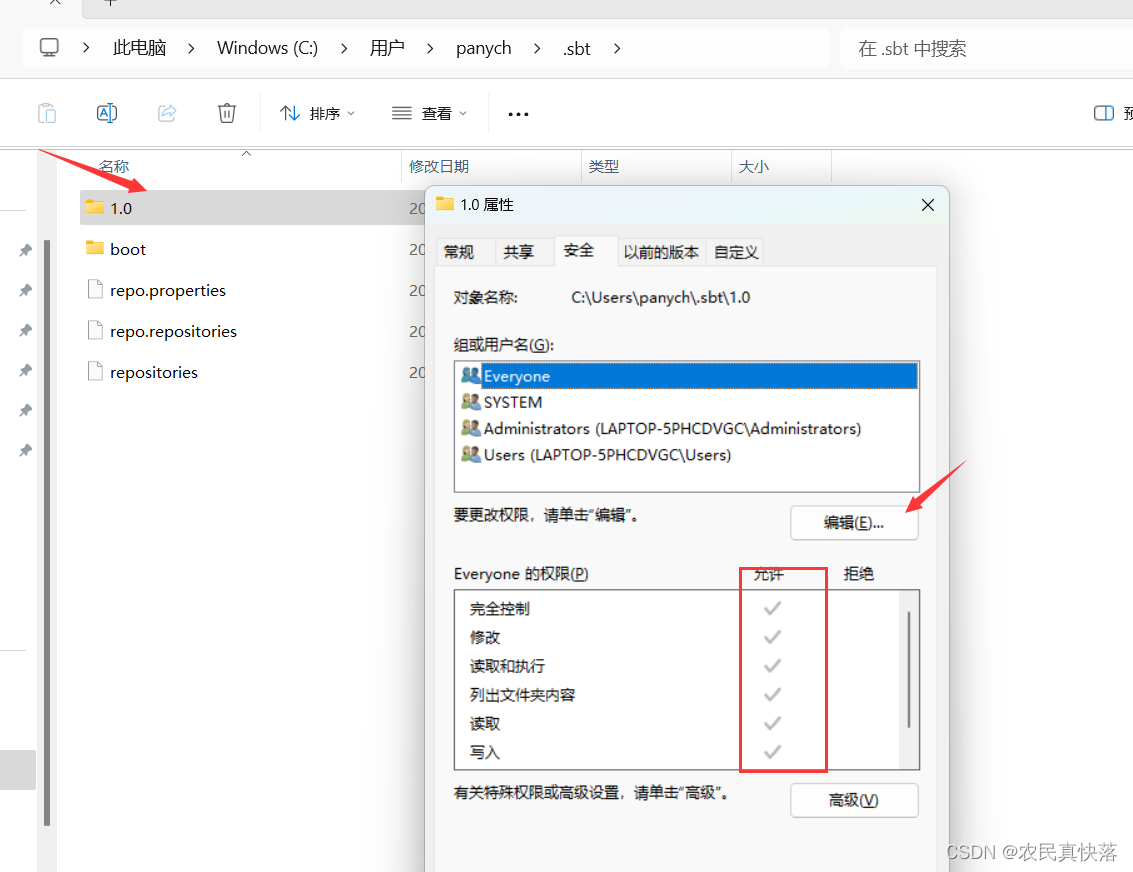
【IC设计】Windows下基于IDEA的Chisel环境安装教程(图文并茂)
Chisel环境安装教程 第一步 安装jdk,配置环境变量第二步 安装sbt,不用配置环境变量第三步 安装idea社区版第四步 离线安装scala的idea插件第五步 配置sbt换源1.切换目录2.创建repositories文件3.配置sbtconfig.txt文件 第六步 使用chisel-tutorial工程运…...
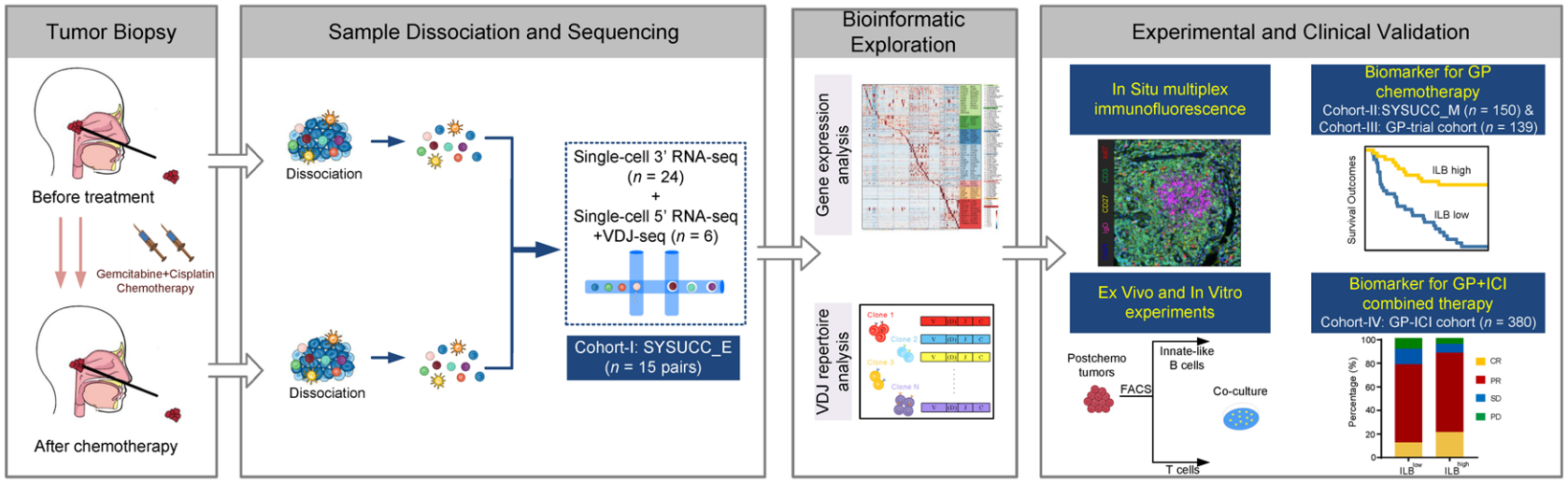
IF=82.9!高分文献解读|吉西他滨联合顺铂化疗激活肿瘤免疫新机制
鼻咽癌(nasopharyngeal carcinoma, NPC)是一种发生于鼻咽部上皮细胞的恶性肿瘤,且高发于中国。吉西他滨联合顺铂(GP)化疗作为鼻咽癌的一种全球标准治疗方案,然而治疗的具体机制目前尚不清楚。中山大学肿瘤防…...
)
【QT+QGIS跨平台编译】之二十八:【Protobuf+Qt跨平台编译】(一套代码、一套框架,跨平台编译)
文章目录 一、Protobuf介绍二、文件下载三、文件分析四、pro文件4.1 libprotobuf4.2 libprotobuf-lite4.3 libprotoc4.4 protocApp五、编译实践一、Protobuf介绍 Protocol Buffers(简称 Protobuf)是由 Google 开发的一种数据序列化协议,就像 XML 或 JSON 一样,但是它更小、…...
.filter(Objects::nonNull).collect(Collectors.toList()))
代码解析:list.stream().filter(Objects::nonNull).collect(Collectors.toList())
这段Java代码是使用了Java 8引入的流(Stream) API来处理集合(比如List)。这个特定的例子展示了如何从一个列表中过滤掉所有的null值,并返回一个新的列表,其中不包含任何null元素。下面是对这段代码的逐步解析: 代码解…...
代驾应用系统(ssm)
登录首页 管理员界面 代驾司机界面 普通用户界面 前台页面 1、系统说明 (1) 框架:spring、springmvc、mybatis、mysql、jsp (2) 系统分为前台系统、后端管理系统 2、欢迎留言联系交流学习讨论:qq 97820625…...

技术栈面试综合整理
Git命令详解 设计模式看了又忘,忘了又看 Linux命令 Java集合Map Java基础 JVM面试题 JVM原理最全、清晰、通俗讲解,五天40小时吐血整理_小爷欣欣-CSDN博客_jvm原理 IO 计算机网络 计算机网络2 jsp 多线程 多线程2 大厂 JAVA 高频面试题 Ja…...

Java中的static关键字
静态变量(类变量)、静态方法(类方法):static声明的属性与方法。 静态变量/静态方法生命周期和类相同,在整个程序执行期间都有效。它有如下特点: 为该类的公用变量,属于类࿰…...

SpringBoot日志插件log4J和slf4J的使用和比较含完整示例
点击下载《SpringBoot日志插件log4J和slf4J的使用和比较含完整示例》 1. 前言 本文主要介绍了在 Spring Boot 框架中如何使用 Log4j 和 Slf4j,并通过对比分析它们的优缺点,帮助读者更好地选择合适的日志记录工具。文章中提供了完整的示例代码ÿ…...
我的世界Java版服务器如何搭建并实现与好友远程联机Minecarft教程
文章目录 1. 安装JAVA2. MCSManager安装3.局域网访问MCSM4.创建我的世界服务器5.局域网联机测试6.安装cpolar内网穿透7. 配置公网访问地址8.远程联机测试9. 配置固定远程联机端口地址9.1 保留一个固定tcp地址9.2 配置固定公网TCP地址9.3 使用固定公网地址远程联机 本教程主要介…...
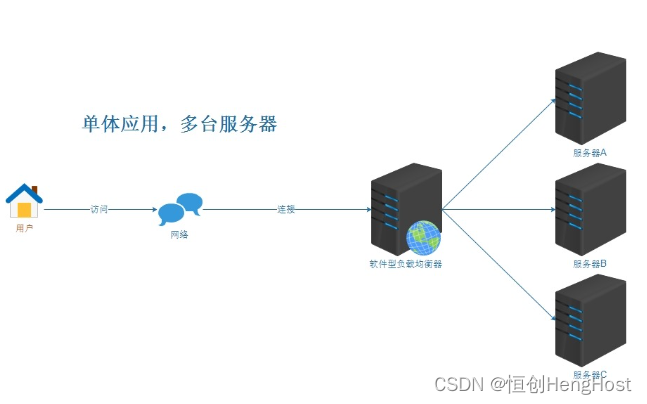
如何进行游戏服务器的负载均衡和扩展性设计?
在进行游戏服务器的负载均衡和扩展性设计时,需要考虑多个方面,以确保服务器的稳定性和可扩展性。以下是一些关键的步骤和考虑因素: 负载均衡的需求分析 在进行负载均衡设计之前,需要深入了解游戏服务器的负载特性和需求。这包括…...

使用docker在3台服务器上搭建基于redis 6.x的一主两从三台均是哨兵模式
一、环境及版本说明 如果服务器已经安装了docker,则忽略此步骤,如果没有安装,则可以按照一下方式安装: 1. 在线安装(有互联网环境): 请看我这篇文章 传送阵>> 点我查看 2. 离线安装(内网环境):请看我这篇文章 传送阵>> 点我查看 说明:假设每台服务器已…...

MPNet:旋转机械轻量化故障诊断模型详解python代码复现
目录 一、问题背景与挑战 二、MPNet核心架构 2.1 多分支特征融合模块(MBFM) 2.2 残差注意力金字塔模块(RAPM) 2.2.1 空间金字塔注意力(SPA) 2.2.2 金字塔残差块(PRBlock) 2.3 分类器设计 三、关键技术突破 3.1 多尺度特征融合 3.2 轻量化设计策略 3.3 抗噪声…...

RocketMQ延迟消息机制
两种延迟消息 RocketMQ中提供了两种延迟消息机制 指定固定的延迟级别 通过在Message中设定一个MessageDelayLevel参数,对应18个预设的延迟级别指定时间点的延迟级别 通过在Message中设定一个DeliverTimeMS指定一个Long类型表示的具体时间点。到了时间点后…...

Day131 | 灵神 | 回溯算法 | 子集型 子集
Day131 | 灵神 | 回溯算法 | 子集型 子集 78.子集 78. 子集 - 力扣(LeetCode) 思路: 笔者写过很多次这道题了,不想写题解了,大家看灵神讲解吧 回溯算法套路①子集型回溯【基础算法精讲 14】_哔哩哔哩_bilibili 完…...

【论文笔记】若干矿井粉尘检测算法概述
总的来说,传统机器学习、传统机器学习与深度学习的结合、LSTM等算法所需要的数据集来源于矿井传感器测量的粉尘浓度,通过建立回归模型来预测未来矿井的粉尘浓度。传统机器学习算法性能易受数据中极端值的影响。YOLO等计算机视觉算法所需要的数据集来源于…...

【JavaSE】绘图与事件入门学习笔记
-Java绘图坐标体系 坐标体系-介绍 坐标原点位于左上角,以像素为单位。 在Java坐标系中,第一个是x坐标,表示当前位置为水平方向,距离坐标原点x个像素;第二个是y坐标,表示当前位置为垂直方向,距离坐标原点y个像素。 坐标体系-像素 …...

html-<abbr> 缩写或首字母缩略词
定义与作用 <abbr> 标签用于表示缩写或首字母缩略词,它可以帮助用户更好地理解缩写的含义,尤其是对于那些不熟悉该缩写的用户。 title 属性的内容提供了缩写的详细说明。当用户将鼠标悬停在缩写上时,会显示一个提示框。 示例&#x…...

Linux C语言网络编程详细入门教程:如何一步步实现TCP服务端与客户端通信
文章目录 Linux C语言网络编程详细入门教程:如何一步步实现TCP服务端与客户端通信前言一、网络通信基础概念二、服务端与客户端的完整流程图解三、每一步的详细讲解和代码示例1. 创建Socket(服务端和客户端都要)2. 绑定本地地址和端口&#x…...

技术栈RabbitMq的介绍和使用
目录 1. 什么是消息队列?2. 消息队列的优点3. RabbitMQ 消息队列概述4. RabbitMQ 安装5. Exchange 四种类型5.1 direct 精准匹配5.2 fanout 广播5.3 topic 正则匹配 6. RabbitMQ 队列模式6.1 简单队列模式6.2 工作队列模式6.3 发布/订阅模式6.4 路由模式6.5 主题模式…...

R语言速释制剂QBD解决方案之三
本文是《Quality by Design for ANDAs: An Example for Immediate-Release Dosage Forms》第一个处方的R语言解决方案。 第一个处方研究评估原料药粒径分布、MCC/Lactose比例、崩解剂用量对制剂CQAs的影响。 第二处方研究用于理解颗粒外加硬脂酸镁和滑石粉对片剂质量和可生产…...
