【C++ 二维前缀和】约会
题目描述
从前,小兔发现了一个神秘的花园。
花园是一个 n 行 m 列的矩阵,第 i 行 j 列的花的美丽度为 ai,j,一个合法的约会场所为任意一个正方形子矩阵,定义子矩阵的浪漫度为这个子矩阵的两条对角线上的花的美丽度之和。
现在小兔想选一个面积大等于 1 的约会场所使得场所的浪漫度最大,以便和小鹿约会,因为小兔忙着 AKIOI ,所以她把这个问题交给了你。输入
第一行,两个正整数 n,m。
接下来是一个 n 行 m 列的矩阵,表示各个位置上花的美丽度。输出
仅一行,一个正整数,表示最大的浪漫度。
样例输入 Copy
3 3 2 -1 3 -4 2 1 1 2 -1样例输出 Copy
7提示
对于 40%的数据,n,m≤10。
对于 100%的数据,1≤n,m≤300,∣ai∣≤104。#include <cstdio> #include <climits> int a[310][310]; long long sumz[310][310],sumf[310][310]; long long ans = LLONG_MIN; int main() {int n, m;scanf("%d%d", &n, &m);for (int i = 1; i <= n; i++){for (int j = 1; j <= m; j++){scanf("%d", &a[i][j]);sumz[i][j] = sumz[i - 1][j - 1] + a[i][j];sumf[i][j] = sumf[i - 1][j + 1] + a[i][j];}}int b = m < n ? m : n, temp;for (int k = 1; k <= b; k++){for (int i = 1; i <= n - k + 1; i++){for (int j = 1; j <= m - k + 1; j++){temp = sumz[i + k - 1][j + k - 1] - sumz[i - 1][j - 1] + sumf[i + k - 1][j] - sumf[i - 1][j + k];if(k & 1) temp -= a[((i << 1) + k - 1) >> 1][((j << 1) + k - 1) >> 1];if (temp > ans) ans = temp;}}}printf("%lld\n", ans);return 0; }
相关文章:

【C++ 二维前缀和】约会
题目描述 从前,小兔发现了一个神秘的花园。 花园是一个 n 行 m 列的矩阵,第 i 行 j 列的花的美丽度为 ai,j,一个合法的约会场所为任意一个正方形子矩阵,定义子矩阵的浪漫度为这个子矩阵的两条对角线上的花的美丽度之和。 现在小兔…...
基于Springboot的社区疫情防控平台
末尾获取源码作者介绍:大家好,我是墨韵,本人4年开发经验,专注定制项目开发 更多项目:CSDN主页YAML墨韵 学如逆水行舟,不进则退。学习如赶路,不能慢一步。 一、项目简介 以往的社区疫情防控管理…...

JAVA中的类方法
一、定义 1.类方法也叫静态方法 格式 访问修饰符 static 数据返回类型 方法名(){} 2.类方法的调用 前提:满足访问修饰符的访问权限 使用方式:类名.类方法名或者对象名.类方法名 二、注意事项 1.类方法中没有this的参数 class D{private int n1 …...

rust嵌入式开发之RTICvsEmbassy
RTIC和Embassy是目前rust嵌入式开发中比较热门的两个框架。本来呢,针对RTIC的移植已经完成了一小半,但在移植过程中感受到了RTIC的不足,正好跳出来全面考察下embassy,本文就是根据目前的尝试结果做个对比总结。 RTIC和Embassy是两…...

Bug地狱 #1 突然宕机,企业级应用到底怎么了
Bug地狱 #1 突然宕机,企业级应用到底怎么了 背景 目前就职的企业经营是一家服务小微门店Saas企业,以进销存管理和客户营销为主体提供订阅服务。项目正式上线可以说是从13年,基础架构是Web和后端使用C# .net,数据库使用SQL Serve…...
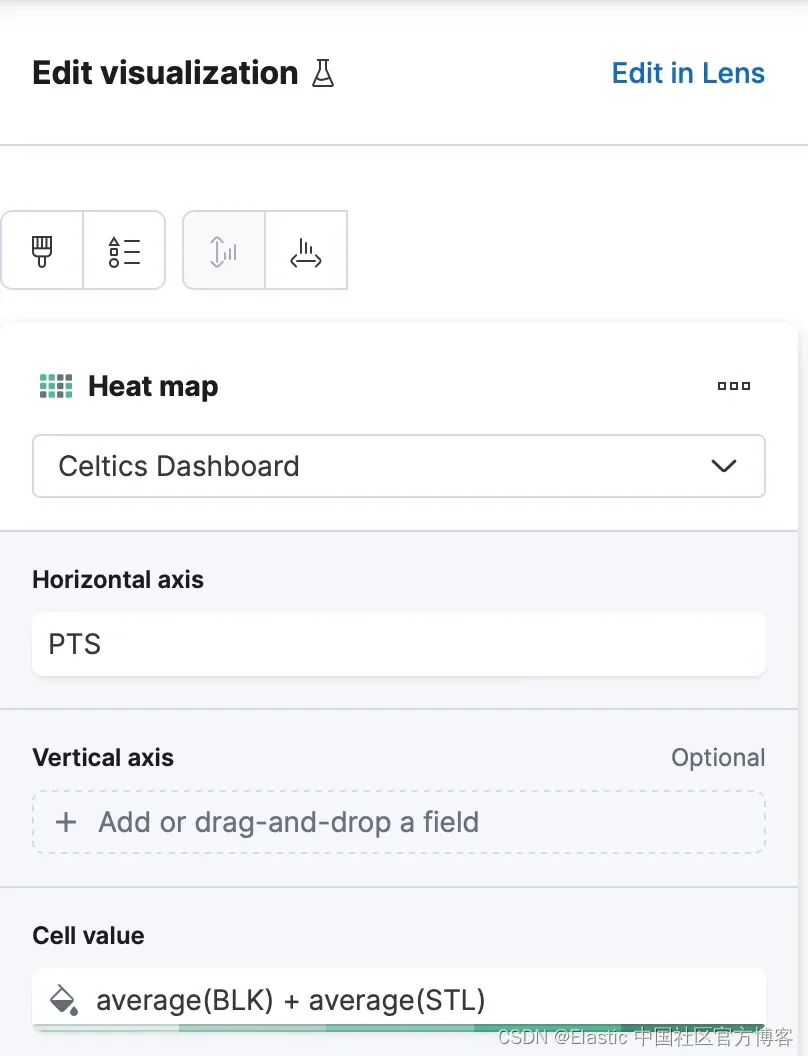
使用 Python、Elasticsearch 和 Kibana 分析波士顿凯尔特人队
作者:来自 Jessica Garson 大约一年前,我经历了一段压力很大的时期,最后参加了一场篮球比赛。 在整个过程中,我可以以一种我以前无法做到的方式断开连接并找到焦点。 我加入的第一支球队是波士顿凯尔特人队。 波士顿凯尔特人队是…...
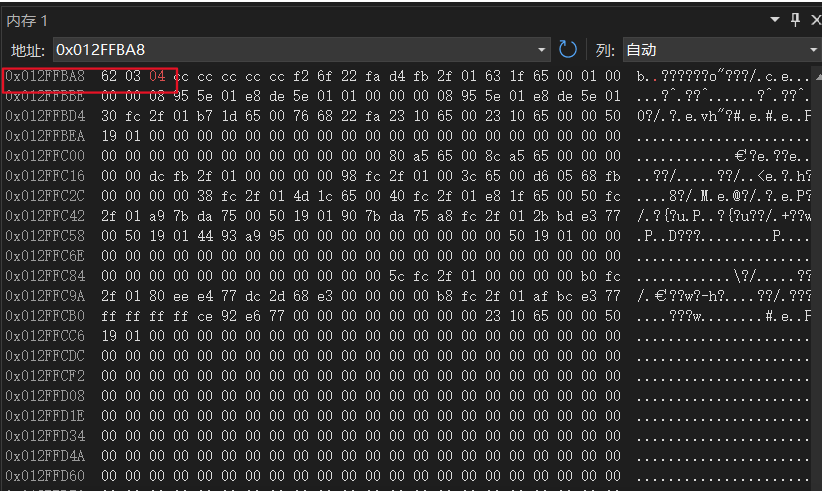
探索C语言结构体:编程中的利器与艺术
✨✨ 欢迎大家来到贝蒂大讲堂✨✨ 🎈🎈养成好习惯,先赞后看哦~🎈🎈 所属专栏:C语言学习 贝蒂的主页:Betty‘s blog 1. 常量与变量 1. 什么是结构体 在C语言中本身就自带了一些数据类型&#x…...
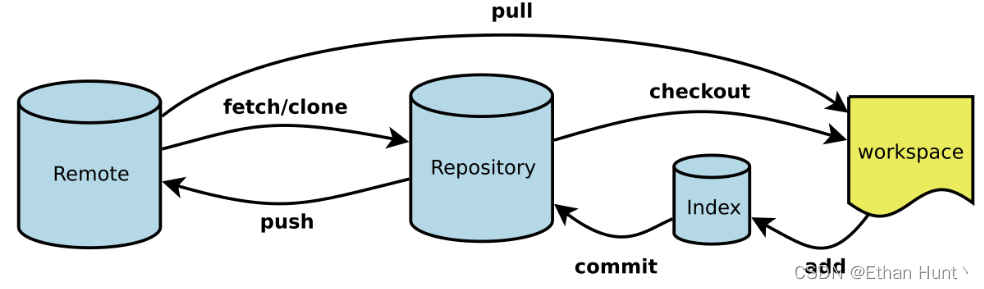
Git介绍与常用命令总结
Git介绍与其常用命令总结 1、Git介绍2、Git的使用3、Git常用命令3.1 初始化仓库3.2 克隆仓库3.3 配置用户信息3.4 提交代码(Commit)3.5 推送代码(Push)3.6 拉取代码(Pull)3.7 分支(Branch)3.8 远程仓库(Remote)3.9 撤销回退本地改动3.10 更新本地仓库与远程仓库 1、Git介绍 Gi…...
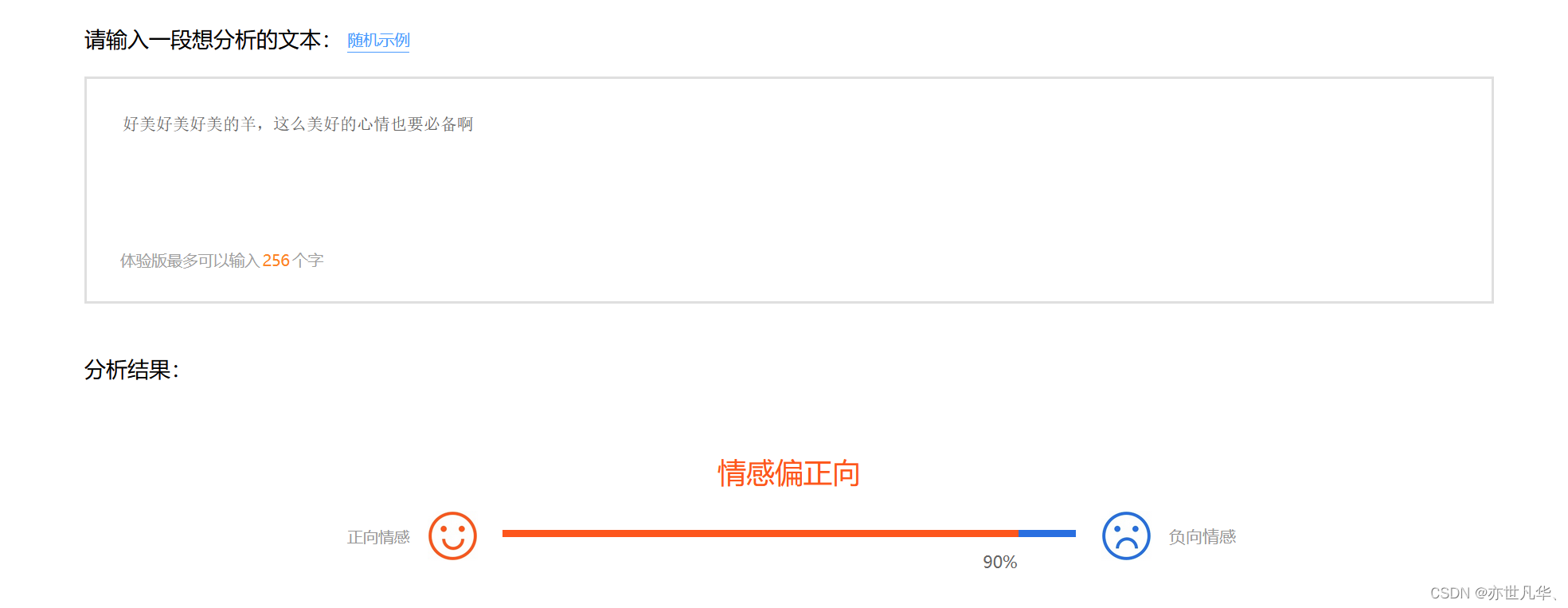
机器学习 | 探索朴素贝叶斯算法的应用
朴素贝叶斯算法是一种基于贝叶斯定理和特征条件独立假设的分类算法。它被广泛应用于文本分类、垃圾邮件过滤、情感分析等领域,并且在实际应用中表现出色。 朴素贝叶斯法是基于贝叶斯定理与特征条件独立假设的分类方法: 1)对于给定的待分类项r…...
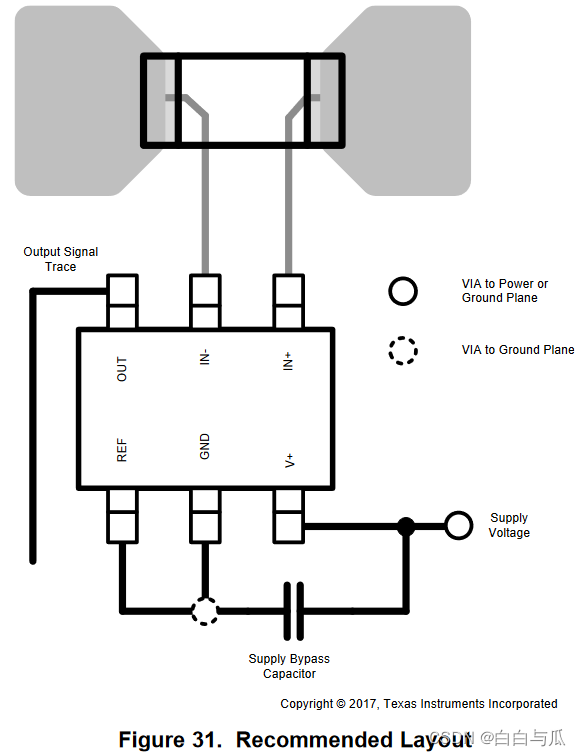
【无刷电机学习】电流采样电路硬件方案
【仅作自学记录,不出于任何商业目的】 目录 AD8210 INA282 INA240 INA199 AD8210 【AD8210数据手册】 在典型应用中,AD8210放大由负载电流通过分流电阻产生的小差分输入电压。AD8210抑制高共模电压(高达65V),并提供接地参考缓冲输出&…...

对于协同过滤算法我自己的一些总结和看法
文章目录 协同过滤算法的基本原理协同过滤算法的分类用户相似度计算UserCF && ItemCF应用场景 协同过滤算法的优缺点优点缺点 协同过滤算法的总结与展望Q&A 协同过滤算法的基本原理 关于协同过滤算法,我看过很多老师写的博客以及一些简单的教程&#x…...
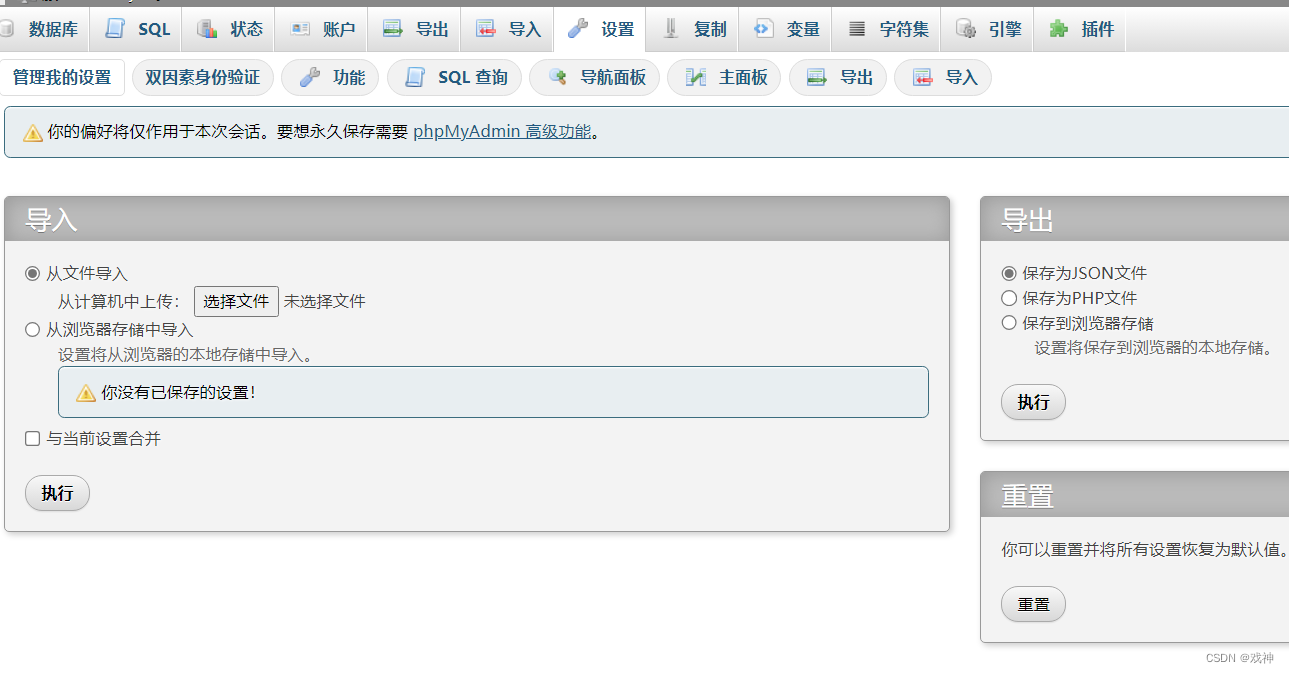
数据库管理phpmyadmin
子任务1-PHPmyadmin软件的使用 本子任务讲解phpmyadmin的介绍和使用操作。 训练目标 1、掌握PHPmyadmin软件的使用方法。 步骤1 phpMyAdmin 介绍 phpmyadmin是一个用PHP编写的软件工具,可以通过web方式控制和操作MySQL数据库。通过phpMyAdmin可以完全对数据库进行…...
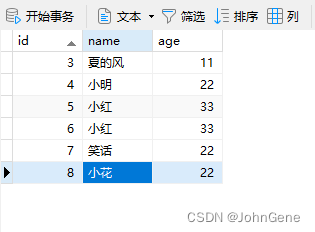
Oracle数据表ID自增操作
一、Oracle ID自增长功能介绍 Oracle数据库默认不支持像 SQLServer、MySQL中的自增长(auto increment)功能,即自动为每一行记录的自增长字段生成下一个值。 二、Oracle ID自增长方法 第一种,通过序列(sequence&#…...

npm WARN deprecated uuid@3.4.0: Please upgrade to version 7 or higher
当使用npm下载vue3-lazy时出现一下错误时的解决方案 报错:npm WARN deprecated uuid3.4.0: Please upgrade to version 7 or higher 尝试使用过一下命令更新 npm install uuidlatest -g 是安装了最新版本的uuid, 再次下载已解决问题 ***但看某些播客依…...

第2节、让电机转起来【51单片机+L298N步进电机系列教程】
↑↑↑点击上方【目录】,查看本系列全部文章 摘要:本节介绍用简单的方式,让步进电机转起来。其目的之一是对电机转动有直观的感受,二是熟悉整个开发流程。本系列教程必要的51单片机基础包括IO口操作、中断、定时器三个部分&#…...

1154: 第多少天
题目描述 定义一个包括年、月、日的结构体变量,读入年、月、日,计算该日在当年中是第几天。注意闰年问题。 输入描述 三个整数,分别表示年、月、日。保证输入是实际存在的日期,且年份在1000至3000之间(包含1000和30…...
【C语言初阶-const作用详解】const修饰变量、const修饰指针(图文详解版)
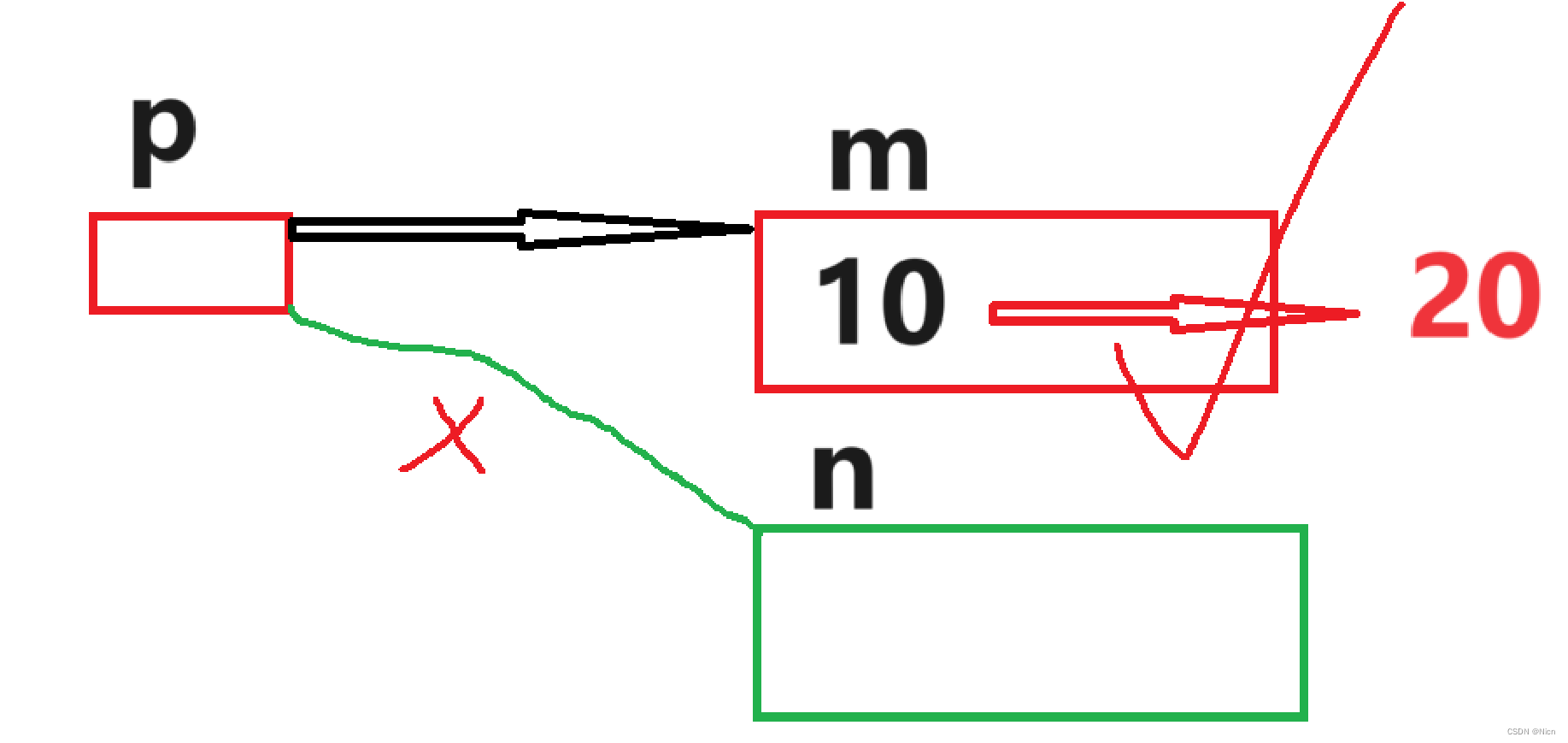
少年,做你认为对的事 目录 少年,做你认为对的事 1.const修饰变量 2.const修饰指针(重要) 代码1: 代码2: 代码3: 编辑 3.结论 1.const修饰变量 const修饰变量将变量赋予了常量属性…...

线程协作工具类【CountDownLatch倒数门闩、Semaphore信号量、CyclicBarrier循环栏栅、Condition接口】
线程协作工具类 CountDownLatch倒数门闩Semaphore信号量CyclicBarrier循环栅栏CyclicBarrier和CountDownLatch区别: Condition接口(条件对象) 转自 极客时间 线程协作工具类就是帮助程序员更容易的让线程之间进行协作,来完成某个业务功能。 CountDownLatch倒数门闩…...
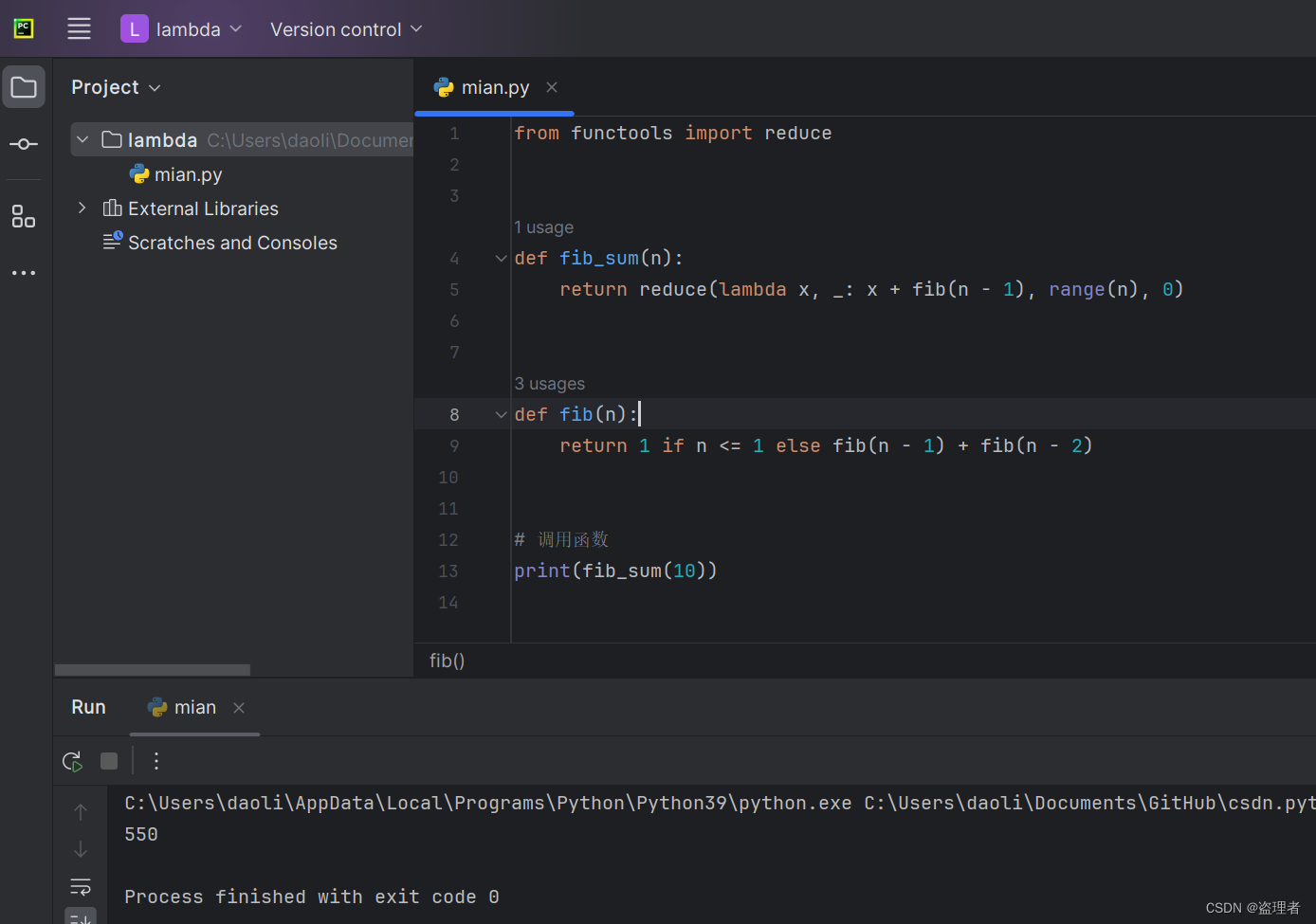
Python 函数式编程进阶:map、filter、reduce
Python 函数式编程进阶:map、filter、reduce 介绍map 函数作用和语法使用 map 函数Lambda 函数的配合应用 filter 函数作用和语法使用 filter 函数Lambda 函数的结合运用 reduce 函数作用和语法使用 reduce 函数典型应用场景 介绍 在函数式编程中,map、…...

大模型|基础_word2vec
文章目录 Word2Vec词袋模型CBOW Continuous Bag-of-WordsContinuous Skip-Gram存在的问题解决方案 其他技巧 Word2Vec 将词转化为向量后,会发现king和queen的差别与man和woman的差别是类似的,而在几何空间上,这样的差别将会以平行的关系进行表…...

Linux云原生安全:零信任架构与机密计算
Linux云原生安全:零信任架构与机密计算 构建坚不可摧的云原生防御体系 引言:云原生安全的范式革命 随着云原生技术的普及,安全边界正在从传统的网络边界向工作负载内部转移。Gartner预测,到2025年,零信任架构将成为超…...

反射获取方法和属性
Java反射获取方法 在Java中,反射(Reflection)是一种强大的机制,允许程序在运行时访问和操作类的内部属性和方法。通过反射,可以动态地创建对象、调用方法、改变属性值,这在很多Java框架中如Spring和Hiberna…...

《基于Apache Flink的流处理》笔记
思维导图 1-3 章 4-7章 8-11 章 参考资料 源码: https://github.com/streaming-with-flink 博客 https://flink.apache.org/bloghttps://www.ververica.com/blog 聚会及会议 https://flink-forward.orghttps://www.meetup.com/topics/apache-flink https://n…...

深入解析C++中的extern关键字:跨文件共享变量与函数的终极指南
🚀 C extern 关键字深度解析:跨文件编程的终极指南 📅 更新时间:2025年6月5日 🏷️ 标签:C | extern关键字 | 多文件编程 | 链接与声明 | 现代C 文章目录 前言🔥一、extern 是什么?&…...

AI书签管理工具开发全记录(十九):嵌入资源处理
1.前言 📝 在上一篇文章中,我们完成了书签的导入导出功能。本篇文章我们研究如何处理嵌入资源,方便后续将资源打包到一个可执行文件中。 2.embed介绍 🎯 Go 1.16 引入了革命性的 embed 包,彻底改变了静态资源管理的…...

均衡后的SNRSINR
本文主要摘自参考文献中的前两篇,相关文献中经常会出现MIMO检测后的SINR不过一直没有找到相关数学推到过程,其中文献[1]中给出了相关原理在此仅做记录。 1. 系统模型 复信道模型 n t n_t nt 根发送天线, n r n_r nr 根接收天线的 MIMO 系…...
与常用工具深度洞察App瓶颈)
iOS性能调优实战:借助克魔(KeyMob)与常用工具深度洞察App瓶颈
在日常iOS开发过程中,性能问题往往是最令人头疼的一类Bug。尤其是在App上线前的压测阶段或是处理用户反馈的高发期,开发者往往需要面对卡顿、崩溃、能耗异常、日志混乱等一系列问题。这些问题表面上看似偶发,但背后往往隐藏着系统资源调度不当…...

在Mathematica中实现Newton-Raphson迭代的收敛时间算法(一般三次多项式)
考察一般的三次多项式,以r为参数: p[z_, r_] : z^3 (r - 1) z - r; roots[r_] : z /. Solve[p[z, r] 0, z]; 此多项式的根为: 尽管看起来这个多项式是特殊的,其实一般的三次多项式都是可以通过线性变换化为这个形式…...

(一)单例模式
一、前言 单例模式属于六大创建型模式,即在软件设计过程中,主要关注创建对象的结果,并不关心创建对象的过程及细节。创建型设计模式将类对象的实例化过程进行抽象化接口设计,从而隐藏了类对象的实例是如何被创建的,封装了软件系统使用的具体对象类型。 六大创建型模式包括…...

解决:Android studio 编译后报错\app\src\main\cpp\CMakeLists.txt‘ to exist
现象: android studio报错: [CXX1409] D:\GitLab\xxxxx\app.cxx\Debug\3f3w4y1i\arm64-v8a\android_gradle_build.json : expected buildFiles file ‘D:\GitLab\xxxxx\app\src\main\cpp\CMakeLists.txt’ to exist 解决: 不要动CMakeLists.…...
