23种设计模式之单例模式
目录
什么是单例模式
单例模式的优点
创建单例模式的三大要点
单例模式的实现方式
饿汉模式
懒汉模式
使用场景
什么是单例模式
单例模式是一种创建型设计模式,它的核心思想是保证一个类只有一个实例,并提供一个全局访问点来访问这个实例。
什么是只有一个实例?
就是在整个应用程序中,只存在该类的一个实例对象,而不是创建多个相同类型的对象。
单例模式的优点
- 全局控制:保证只有一个实例,这样就可以严格的控制用户怎样访问它何时访问它;
- 节省资源:只有一个实例存在,避免多次创建相同的对象,从而节省了系统资源;
- 提高性能:单例模式可以实现懒加载,只有在需要的时候才进行实例化。
创建单例模式的三大要点
- 私有的构造函数:防止外部代码直接创建类的实例
- 私有的静态变量:保证该类的唯一实例
- 公有的静态方法:通过这个公有的静态方法来获取实例(全局访问点)
单例模式的实现方式
饿汉式:在类加载时就已经完成了实例的创建,不管后面创建的实例有没有使用,先创建再说。
懒汉式: 只有在请求实例时才会创建,如果首次请求时还没创建,就创建一个新的实例,如果已经创建了就返回已有的实例。
优缺点比较:
- 饿汉模式在刚开始就创建了实例,不存在线程安全问题,但是有可能创建的实例一直没用,会造成资源浪费;
- 懒汉模式只有在请求的时候才会创建不存在资源浪费,但是如果有多个线程同时访问getInstance()并且同一时刻检测到没有创建实例,就可能会同时创建实例,违背了单例模式,可以用互斥锁来解决。
饿汉模式
//饿汉模式:在类加载的时候就创建实例,可能会没有使用而造成资源浪费
public class Singleton_e {
// 私有的静态实例变量private static final Singleton_e instance=new Singleton_e();private Singleton_e(){
// 私有的构造方法}
// 公有的静态访问方法public static Singleton_e getInstance(){return instance;}
}懒汉模式
public class Singleton_l {
// 懒汉模式:在请求实例的时候才会创建
// 私有的静态变量private static Singleton_l instance;
// 私有的构造方法private Singleton_l(){}
// 公有的静态方法
// 使用双重校验锁来确保线程安全public static Singleton_l getInstance(){if(instance==null){synchronized (Singleton_l.class){if(instance==null){return new Singleton_l();}}}return instance;}
}使用场景
1. 资源共享多个模块共享某个资源的时候,可以使⽤单例模式,⽐如说应⽤程序需要⼀个全局的配置管理器来存储和管理配置信息。2. 只有⼀个实例当系统中某个类只需要⼀个实例来协调⾏为的时候,可以考虑使⽤单例模式, ⽐如说管理应⽤程序中的缓存,确保只有⼀个缓存实例,避免重复的缓存创建和管理。3. 懒加载如果对象创建本身就⽐较消耗资源,⽽且可能在整个程序中都不⼀定会使⽤,可以使⽤单例模式实现懒加载。
相关文章:

23种设计模式之单例模式
目录 什么是单例模式 单例模式的优点 创建单例模式的三大要点 单例模式的实现方式 饿汉模式 懒汉模式 使用场景 什么是单例模式 单例模式是一种创建型设计模式,它的核心思想是保证一个类只有一个实例,并提供一个全局访问点来访问这个实例。 什…...

leetCode 30天
题太难了,就来一个N皇后吧 51. N 皇后 class Solution { private:vector<vector<string>> res;void backtracking(int n, int row, vector<string>& chessboard){if (row n){res.push_back(chessboard);return;}for (int col 0; col<n;…...
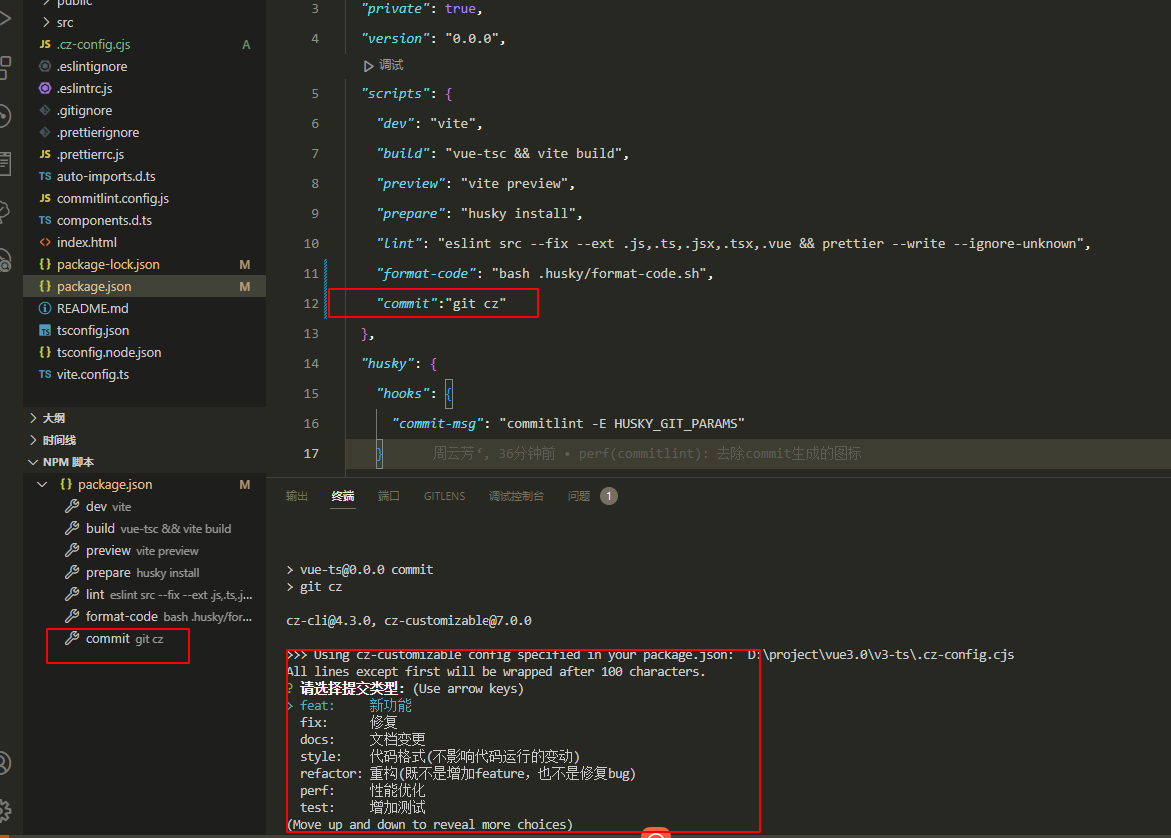
vue3+vite+ts 配置commit强制码提交规范配置 commitlint
配置 git 提交时的 commit 信息,统一提交 git 提交规范 安装命令: npm install -g commitizen npm i cz-customizable npm i commitlint/config-conventional commitlint/cli -D 文件配置 根路径创建文件 commitlint.config.js module.exports {// 继承的规…...
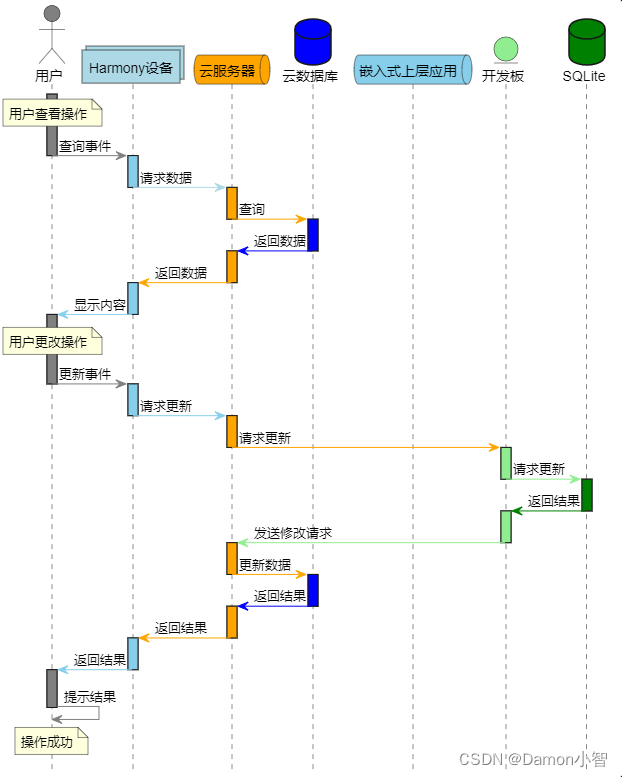
PlateUML绘制UML图教程
UML(Unified Modeling Language)是一种通用的建模语言,广泛用于软件开发中对系统进行可视化建模。PlantUML是一款强大的工具,通过简单的文本描述,能够生成UML图,包括类图、时序图、用例图等。PlantUML是一款…...
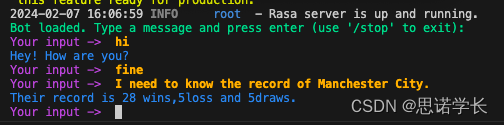
自然语言处理(NLP)——使用Rasa创建聊天机器人
1 基本概念 1.1 自然语言处理的分类 IR-BOT:检索型问答系统 Task-bot:任务型对话系统 Chitchat-bot:闲聊系统 1.2 任务型对话Task-Bot:task-oriented bot 这张图展示了一个语音对话系统(或聊天机器人)的基本组成部分和它们之间的…...
使用虚拟主机部署多站点
网站目录权限的管理和虚拟主机的配置。 目录权限控制...

Openresty+Lua+Redis实现高性能缓存
一、背景 当我们的程序需要提供较高的并发访问时,往往需要在程序中引入缓存技术,通常都是使用Redis作为缓存,但是要再更进一步提升性能的话,就需要尽可能的减少请求的链路长度,比如可以将访问Redis缓存从Tomcat服务器…...
基于Vue2用keydown、keyup事件实现长按键盘任意键(或组合键)3秒触发自定义事件(以F1键为例)
核心代码 <template></template> <script> export default {created() {//监听长按快捷键addEventListener("keydown", this.keydown);addEventListener("keyup", this.keyup);},destroyed(d) {//移除长按快捷键removeEventListener(&…...
【C#】.net core 6.0 设置根目录下某个文件夹可访问,访问创建的图片等资源
欢迎来到《小5讲堂》 大家好,我是全栈小5。 这是《C#》系列文章,每篇文章将以博主理解的角度展开讲解, 特别是针对知识点的概念进行叙说,大部分文章将会对这些概念进行实际例子验证,以此达到加深对知识点的理解和掌握。…...
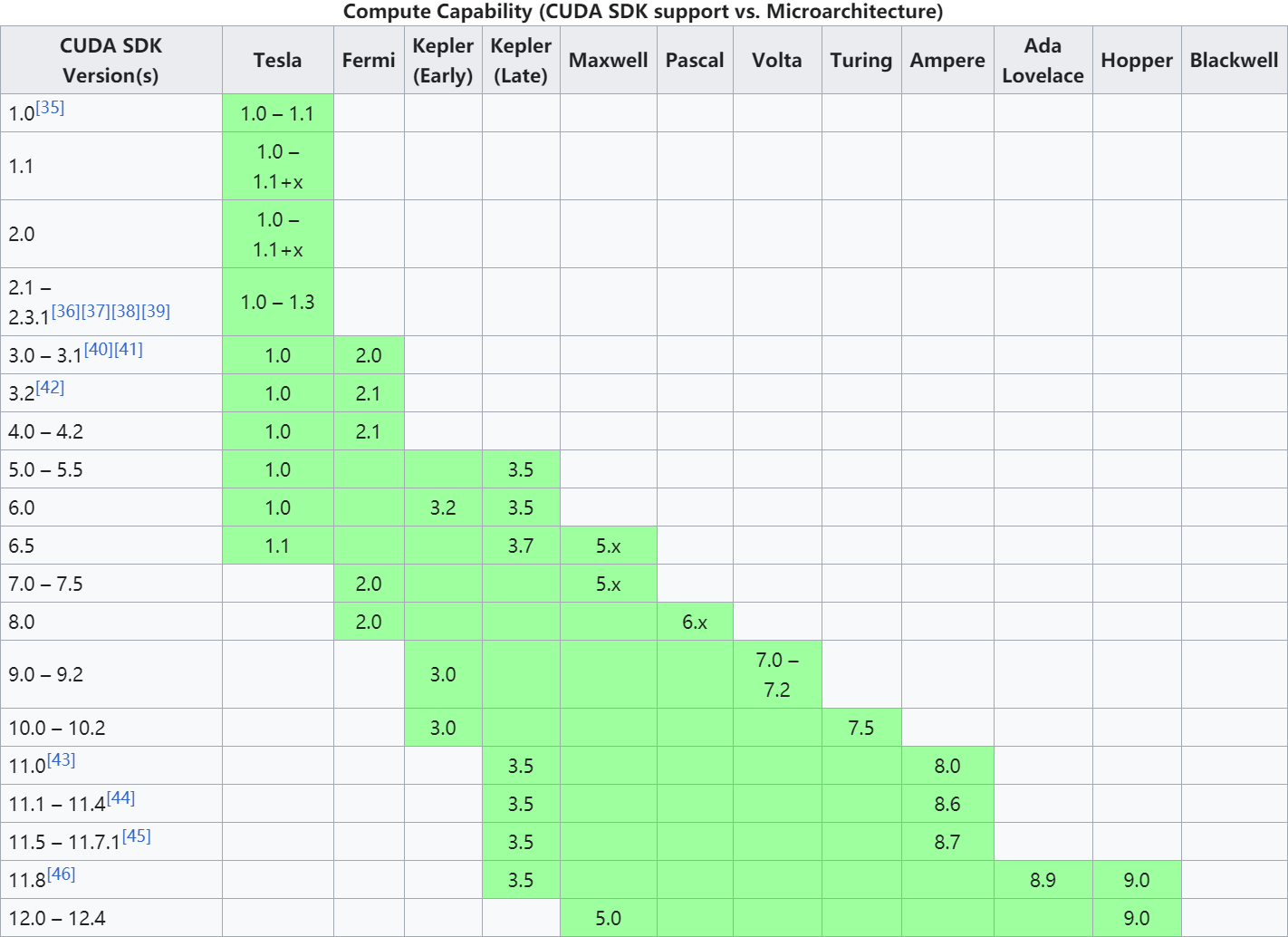
报错ValueError: Unknown CUDA arch (8.6) or GPU not supported
文章目录 问题描述解决方案参考文献 问题描述 报错 ValueError: Unknown CUDA arch (8.6) or GPU not supported 本人显卡为 RTX 3060,CUDA 为 10.2,PyTorch 为 1.5 解决方案 修改 C:\Users\Administrator\Envs\test\Lib\site-packages\torch\utils\c…...

Golang 并发 Cond条件变量
Golang 并发 Cond条件变量 背景 编写代码过程中, 通常有主协程和多个子协程进行协作的过程,比如通过 WaitGroup 可以实现当所有子协程完成之后, 主协程再继续执行。 如上的场景是主协程等待子协程达到某个状态再继续运行。 但是反过来怎么…...

linux 下 chrome 无法在设置里面配置代理的解决方法
文章目录 [toc]解决方法查找 chrome 命令路径查看 chrome 启动文件方式一方法二 在 linux 环境下,使用 chrome 没办法像 firefox 一样在设置里面配置代理,打开 chrome 的设置会有下面的内容显示 When running Google Chrome under a supported desktop e…...

C#上位机与三菱PLC的通信03--MC协议之A-1E报文解析
1、MC协议帧 MC协议可以在串口通信,也可以在以太网通信,有A-1E和Qna-3E两种模式,这两种都是三菱PLC通信协议中比较常用的两种,一般我们使用比较多的是以太网通信,对于FX5U系列/Q系列/Qna系列/L系列的PLC,…...

nodeJS 的 npm 设置国内高速镜像之淘宝镜像的方法
1、我们知道 nodeJS 是老外搞出来的,服务器放在了国外,国内的小朋友访问起来会比较慢,阿里巴巴的淘宝给出了有力支持,现在我们就将 nodeJS 的镜像地址切换为国内的淘宝镜像。 2、查看当前的镜像地址: npm get registr…...

Nginx方向代理和负载均衡配置
1. Nginx介绍 2.Nginx常用命令 cd /usr/local/nginx/sbin/ ./nginx 启动 ./nginx -s stop 停止 ./nginx -s quit 安全退出 ./nginx -s reload 重新加载配置文件 如果我们修改了配置文件,就需要重新加载。 ps aux|grep nginx 查看nginx进程3.nginx配置文件 …...

贪心算法篇
“靠漫步,将生趣填饱~” 贪心算法简介? 贪心算法(Greedy Algorithm),也称为贪婪算法,是一种在解决问题时采取贪心策略的方法。其基本原理是很简单的: “在每个决策点上都选择当下看似最好的选项…...

springboot/ssm大学生就业服务平台就业招聘宣传管理系统Java系统
springboot(ssm大学生就业服务平台 就业招聘宣传管理系统Java系统 开发语言:Java 框架:springboot(可改ssm) vue JDK版本:JDK1.8(或11) 服务器:tomcat 数据库:mysql…...

上下固定中间自适应布局
实现上下固定中间自适应布局 1.通过position:absolute实现 定义如下结构 <body> <div class"container"> <div class"top"></div> <div class"center"></div> <div class"bottom&…...
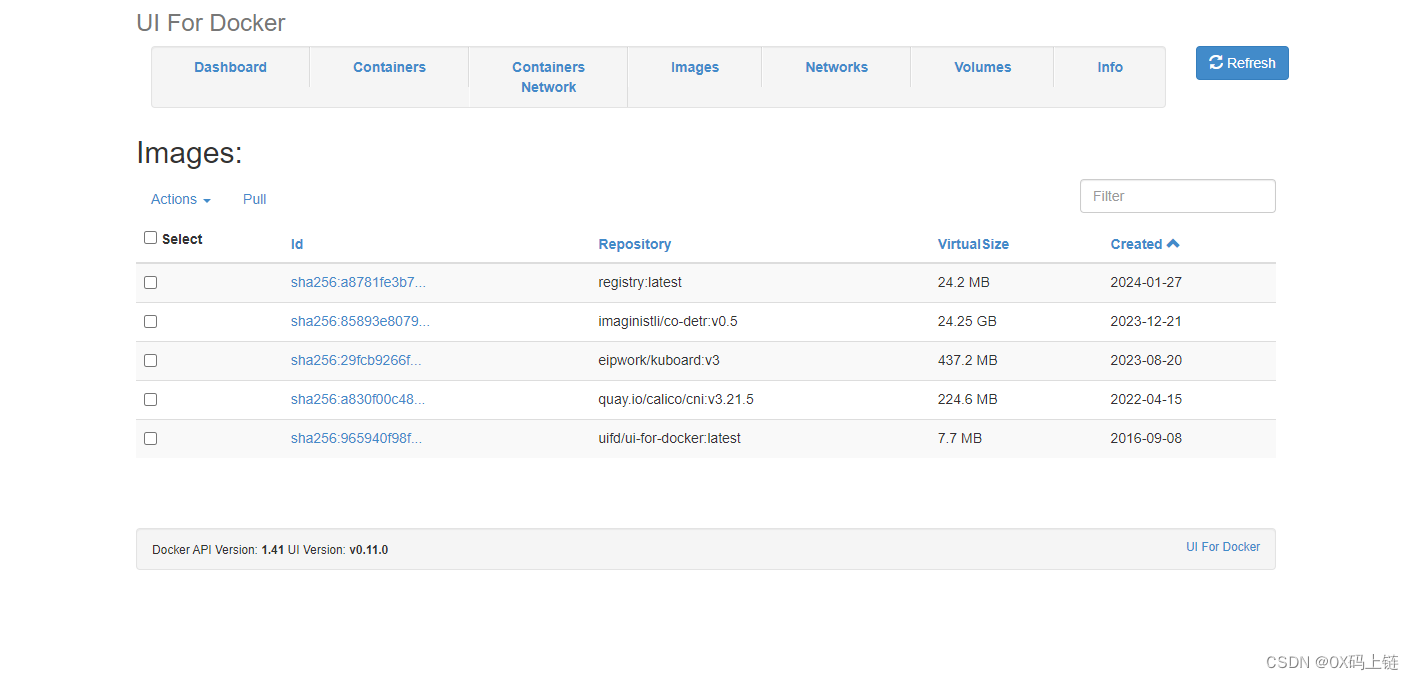
3分钟部署完成Docker Registry及可视化管理工具Docker-UI
安装docker-registry 由于镜像文件会非常占用空间,因此需要选择一个磁盘充裕的位置来存放镜像数据。 这里设置为:-v /data/registry:/var/lib/registry,其中/data/registry是宿主机存放数据的位置。 docker run -d -p 5000:5000 --restart…...
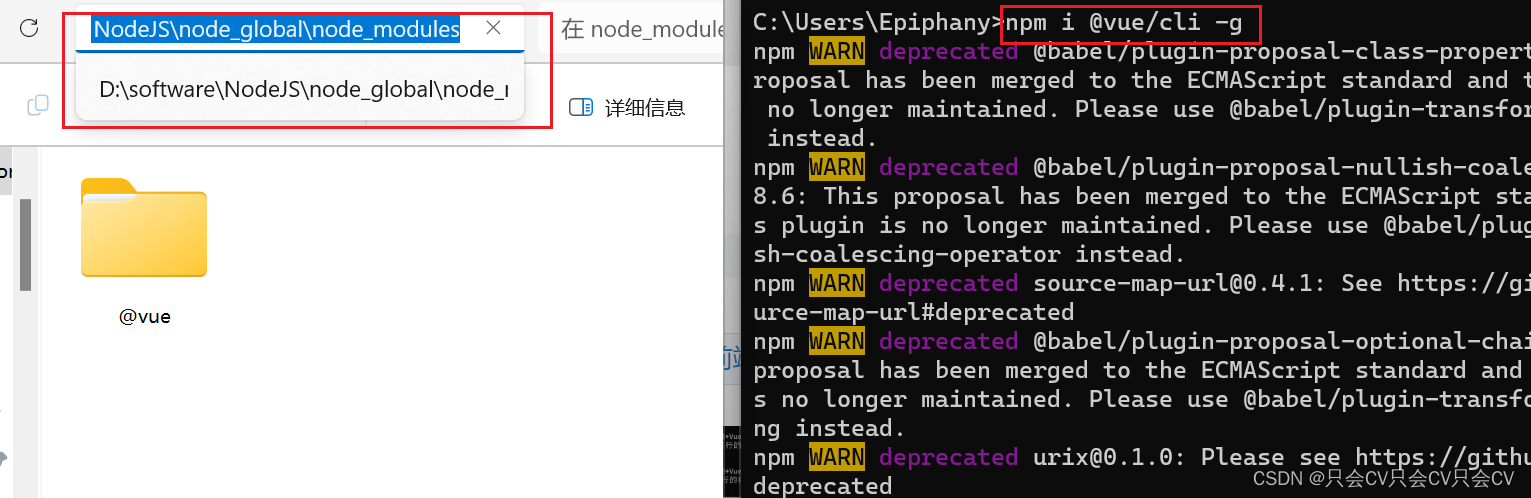
【npm】修改npm全局安装包的位置路径
问题 全局安装的默认安装路径为:C:\Users\admin\AppData\Roaming\npm,缓存路径为:C:\Users\admin\AppData\Roaming\npm_cache(其中admin为自己的用户名)。 由于默认的安装路径在C盘,太浪费C盘内存啦&#…...
结构体的进阶应用)
基于算法竞赛的c++编程(28)结构体的进阶应用
结构体的嵌套与复杂数据组织 在C中,结构体可以嵌套使用,形成更复杂的数据结构。例如,可以通过嵌套结构体描述多层级数据关系: struct Address {string city;string street;int zipCode; };struct Employee {string name;int id;…...

手游刚开服就被攻击怎么办?如何防御DDoS?
开服初期是手游最脆弱的阶段,极易成为DDoS攻击的目标。一旦遭遇攻击,可能导致服务器瘫痪、玩家流失,甚至造成巨大经济损失。本文为开发者提供一套简洁有效的应急与防御方案,帮助快速应对并构建长期防护体系。 一、遭遇攻击的紧急应…...

Appium+python自动化(十六)- ADB命令
简介 Android 调试桥(adb)是多种用途的工具,该工具可以帮助你你管理设备或模拟器 的状态。 adb ( Android Debug Bridge)是一个通用命令行工具,其允许您与模拟器实例或连接的 Android 设备进行通信。它可为各种设备操作提供便利,如安装和调试…...
Cesium相机控制)
三维GIS开发cesium智慧地铁教程(5)Cesium相机控制
一、环境搭建 <script src"../cesium1.99/Build/Cesium/Cesium.js"></script> <link rel"stylesheet" href"../cesium1.99/Build/Cesium/Widgets/widgets.css"> 关键配置点: 路径验证:确保相对路径.…...

MongoDB学习和应用(高效的非关系型数据库)
一丶 MongoDB简介 对于社交类软件的功能,我们需要对它的功能特点进行分析: 数据量会随着用户数增大而增大读多写少价值较低非好友看不到其动态信息地理位置的查询… 针对以上特点进行分析各大存储工具: mysql:关系型数据库&am…...

从深圳崛起的“机器之眼”:赴港乐动机器人的万亿赛道赶考路
进入2025年以来,尽管围绕人形机器人、具身智能等机器人赛道的质疑声不断,但全球市场热度依然高涨,入局者持续增加。 以国内市场为例,天眼查专业版数据显示,截至5月底,我国现存在业、存续状态的机器人相关企…...

【快手拥抱开源】通过快手团队开源的 KwaiCoder-AutoThink-preview 解锁大语言模型的潜力
引言: 在人工智能快速发展的浪潮中,快手Kwaipilot团队推出的 KwaiCoder-AutoThink-preview 具有里程碑意义——这是首个公开的AutoThink大语言模型(LLM)。该模型代表着该领域的重大突破,通过独特方式融合思考与非思考…...

江苏艾立泰跨国资源接力:废料变黄金的绿色供应链革命
在华东塑料包装行业面临限塑令深度调整的背景下,江苏艾立泰以一场跨国资源接力的创新实践,重新定义了绿色供应链的边界。 跨国回收网络:废料变黄金的全球棋局 艾立泰在欧洲、东南亚建立再生塑料回收点,将海外废弃包装箱通过标准…...

【算法训练营Day07】字符串part1
文章目录 反转字符串反转字符串II替换数字 反转字符串 题目链接:344. 反转字符串 双指针法,两个指针的元素直接调转即可 class Solution {public void reverseString(char[] s) {int head 0;int end s.length - 1;while(head < end) {char temp …...

C++中string流知识详解和示例
一、概览与类体系 C 提供三种基于内存字符串的流,定义在 <sstream> 中: std::istringstream:输入流,从已有字符串中读取并解析。std::ostringstream:输出流,向内部缓冲区写入内容,最终取…...
