【数据结构】堆(创建,调整,插入,删除,运用)
目录
堆的概念:
堆的性质:
堆的存储方式:
堆的创建 :
堆的调整:
向下调整:
向上调整:
堆的创建:
建堆的时间复杂度:
向下调整:
向上调整:
堆的插入与删除:
堆的插入:
堆的删除:
堆的应用:
1.PriorityQueue的实现
2.堆排序:
3.Top-k问题
结语:
堆的概念:
如果有一个关键码的集合K = {k0,k1, k2,…,kn-1},把它的所有元素按完全二叉树的顺序存储方式存储 在一 个一维数组中,并满足:Ki = K2i+1 且 Ki >= K2i+2) i = 0,1,2…,则称为小堆(或大堆)。将根节点最大的堆叫做最大堆或大根堆,根节点最小的堆叫做最小堆或小根堆。
堆的性质:
(1)堆中某个节点的值总是不大于(大根堆)或不小于(小根堆)其父节点的值。
(2)堆总是一棵完全二叉树。
具体如下图。

堆的存储方式:
从堆的概念可知,堆是一棵完全二叉树,因此可以层序的规则采用顺序的方式来高效存储。
注意:对于非完全二叉树,则不适合使用顺序方式进行存储,因为为了能够还原二叉树,空间中必须要存储空节点,就会导致空间利用率比较低。
将元素存储到数组中后,可以根据二叉树章节的性质对树进行还原。假设i为节点在数组中的下标,则有:
(1)如果i为0,则i表示的节点为根节点,否则i节点的双亲节点为 (i - 1)/2.
(2)如果2 * i + 1 小于节点个数,则节点i的左孩子下标为2 * i + 1,否则没有左孩子。
(3)如果2 * i + 2 小于节点个数,则节点i的右孩子下标为2 * i + 2,否则没有右孩子。
堆的创建 :
为了使文章可读性更高下面给出测试堆类的基本代码,下面文章给出的代码均围绕这上面来。
elem:是一个类里面的数组(方便后序操作)
usedSize:是记录数组里面有多少个元素(不是数组容量)
TestHeap:构造方法为了简便把数组容量设为10,大小可以自己调整
initElem:初始化
public class TestHeap {public int[] elem;public int usedSize;public TestHeap(){elem = new int[10];}public void initElem(int[] array){for(int i = 0;i < array.length;i++){elem[i] = array[i];usedSize++;}}
}堆的调整:
堆有向上调整和向下调整两种调整方式,在创建时我们采用向下调整方式,这样的时间复杂度比较低。故下面主要讲解向下过程(以大堆为例) 步骤如下:
向下调整:
1. 让parent标记需要调整的节点,child标记parent的左孩子(注意:parent如果有孩子一定先是有左孩子)。
2. 如果parent的左孩子存在,即:child < size, 进行以下操作,直到parent的左孩子不存在。
(1)parent右孩子是否存在,存在找到左右孩子中最小的孩子,让child进行标记。
(2)将parent与较小的孩子child比较,如果:
a:parent小于较小的孩子child,调整结束。
b:否则:交换parent与较小的孩子child,交换完成之后,parent中大的元素向下移动,可能导致子 树不满足对的性质,因此需要继续向下调整,即parent = child;child = parent*2+1; 然后继续。
以数组{ 27,15,19,18,28,34,65,49,25,37 }为例调整完变成。

对应的代码如下:
如果想要转换成小堆的话把大于号小于号改一改即可,故下面不在过多描述。
private void siftDown1(int parent,int end){int child = parent*2+1;while(child < end){if(child+1 < usedSize && elem[child] < elem[child+1]){child++;}if(elem[child] > elem[parent]){swap(child,parent);parent = child;child = parent*2+1;}else{break;}}}为了使代码整洁故再实现一个swap方法。
private void swap(int i,int j){int tmp = elem[i];elem[i] = elem[j];elem[j] = tmp;}注意:在调整以parent为根的二叉树时,必须要满足parent的左子树和右子树已经是堆了才可以向下调整。 时间复杂度分析:最坏的情况即图示的情况,从根一路比较到叶子,比较的次数为完全二叉树的高度,即时间复杂度为O(logn)log下标是以2为底的。
向上调整:
具体过程如图(按照插入的80走的路径):

代码如下:
先找新结点的parent的下标再child大于0的情况下循环进行比较交换,一旦发现不满足条件的立刻跳出循环,因为在使用向上调整之前堆已经排序好了。
public void siftUp(int child){int parent = (child-1)/2;while(child > 0){if(elem[child] > elem[parent]){swap(child,parent);child = parent;parent = (child-1)/2;}else{break;}}}堆的创建:
如图所示是从最后一个结点的父亲结点开始遍历每一个结点都调用siftdown1进行向下调整,之后不断减减直到小于0(下标)。

代码如下:
public void createBigHeap(){for(int parent = (usedSize-1-1)/2;parent >= 0;parent--){siftDown1(parent,usedSize);}}运行结果:
通过观察elem的元素我们可以发现向下调整成功。💖

建堆的时间复杂度:
向下调整:
因为堆是完全二叉树,而满二叉树也是完全二叉树,此处为了简化使用满二叉树来证明(时间复杂度本来看的就是 近似值,多几个节点不影响最终结果):如图:

向上调整:
如图:

经过比较我们选择时间复杂度较低的来进行堆的创建即向下调整,至于向上调整我们用于堆的堆的插入与删除。
堆的插入与删除:
堆的插入:
堆的插入总共需要两个步骤:
(1)先将元素放入到底层空间中(注意:空间不够时需要扩容).
(2)将最后新插入的节点向上调整,直到满足堆的性质.
代码如下:
isFull用来判断是否需要扩容
public boolean isFull(){return usedSize == elem.length;}siftUp用来向上调整,先找到新参数的parent结点, 传入siftup的参数为新offer进来的参数。
public void offer(int val){//1.判断满if(isFull()){this.elem = Arrays.copyOf(elem,elem.length*2);}elem[usedSize] = val;usedSize++;siftUp(usedSize-1);}运行结果如下:
我们可以发现成功增加数据并完成排序。

堆的删除:
注意:堆的删除一定删除的是堆顶元素。具体如下:
(1) 将堆顶元素对堆中最后一个元素交换。
(2) 将堆中有效数据个数减少一个。
(3)对堆顶元素进行向下调整 。
代码如下:
其实就是把最后一个元素的空间腾出来。
public int poll(){int tmp = elem[0];swap(0,usedSize-1);usedSize--;siftDown1(0,usedSize);return tmp;}运行结果如下:
可以看到65被成功删除并且数组的序列没有改变

堆的应用:
1.PriorityQueue的实现
可以使用堆来实现优先队列,由于java语言有自带的优先队列故这里不在实现给出它的常用方法直接调用即可。
| 函数名 | 功能介绍 |
| boolean offer(E e) | 插入元素e,插入成功返回true,如果e对象为空,抛出NullPointerException异常,注意:空间不够时候会进行扩容 |
| E peek() | 获取优先级最高的元素,如果优先级队列为空,返回null |
| E poll() | 移除优先级最高的元素并返回,如果优先级队列为空,返回null |
| int size() | 获取有效元素的个数 |
| void clear() | 清空 |
| boolean isEmpty() | 检测优先级队列是否为空,空返回true |
2.堆排序:
堆排序即利用堆的思想来进行排序,总共分为两个步骤:
1. 建堆
升序:建大堆
降序:建小堆
2. 利用堆删除思想来进行排序
建堆和堆删除中都用到了向下调整,因此掌握了向下调整,就可以完成堆排序。
具体过程如下:
代码后序会将8大排序整理成一篇排序专项。

3.Top-k问题
TOP-K问题:即求数据集合中前K个最大的元素或者最小的元素,一般情况下数据量都比较大。
比如:专业前10名、世界500强、富豪榜、游戏中前100的活跃玩家等。 对于Top-K问题,能想到的最简单直接的方式就是排序,但是:如果数据量非常大,排序就不太可取了(可能数据都 不能一下子全部加载到内存中)。最佳的方式就是用堆来解决,基本思路如下:
1. 用数据集合中前K个元素来建堆
(1)前k个最大的元素,则建小堆.
(2)前k个最小的元素,则建大堆。
2. 用剩余的N-K个元素依次与堆顶元素来比较,不满足则替换堆顶元素
将剩余N-K个元素依次与堆顶元素比完之后,堆中剩余的K个元素就是所求的前K个最小或者最大的元素。
不要用Arrays.sort来做这道题,因为这是一道面试题,用sort就可以快速结束面试,回家等通知了。
top-k问题
使用堆的AC优化代码:
class Imp implements Comparator<Integer>{@Overridepublic int compare(Integer o1,Integer o2){return o2.compareTo(o1);}}
class Solution {public int[] smallestK(int[] arr, int k) {Imp imp = new Imp();PriorityQueue<Integer> priorityqueue = new PriorityQueue<>(imp);int[] ans = new int[k];if(k == 0){return ans;}for(int i = 0;i < k; i++){priorityqueue.offer(arr[i]);}for(int i = k;i < arr.length; i++){int tmp = priorityqueue.peek();if(arr[i] < tmp){priorityqueue.poll();priorityqueue.offer(arr[i]);}}for(int i = 0;i < k; i++){ans[i] = priorityqueue.poll();}return ans;}
}结语:
其实写博客不仅仅是为了教大家,同时这也有利于我巩固自己的知识点,和一个学习的总结,由于作者水平有限,对文章有任何问题的还请指出,接受大家的批评,让我改进,如果大家有所收获的话还请不要吝啬你们的点赞收藏和关注,这可以激励我写出更加优秀的文章。

相关文章:

【数据结构】堆(创建,调整,插入,删除,运用)
目录 堆的概念: 堆的性质: 堆的存储方式: 堆的创建 : 堆的调整: 向下调整: 向上调整: 堆的创建: 建堆的时间复杂度: 向下调整: 向上调整ÿ…...
v-if 和v-for的联合规则及示例
第073个 查看专栏目录: VUE ------ element UI 专栏目标 在vue和element UI联合技术栈的操控下,本专栏提供行之有效的源代码示例和信息点介绍,做到灵活运用。 提供vue2的一些基本操作:安装、引用,模板使用,computed&a…...

各互联网企业测绘资质调研
公司子公司产品产品介绍资质获得资质时间阿里巴巴高德高德地图作为阿里的全资子公司,中国领先的数字地图内容、导航和位置服务解决方案提供商,互联网地图行业龙头,2021年4月高德实现全月平均日活跃用户数超过1亿的重要里程碑,稳居…...
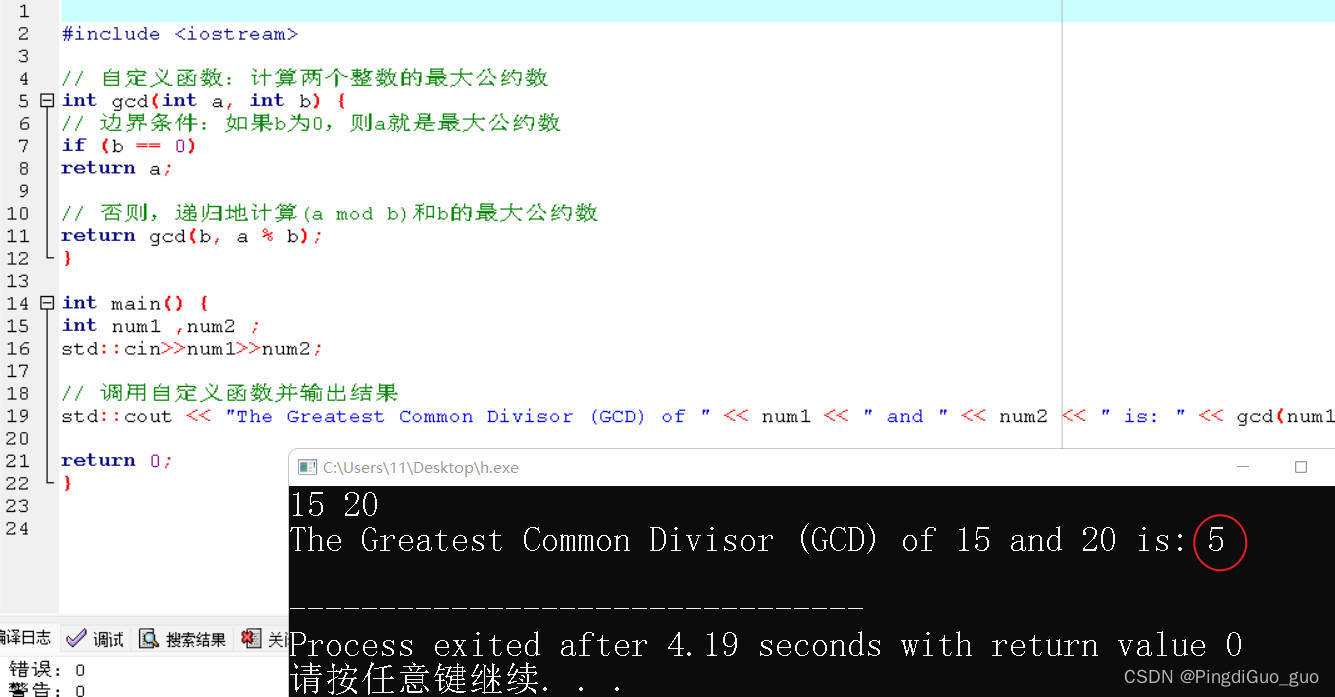
C++自定义函数详解
个人主页:PingdiGuo_guo 收录专栏:C干货专栏 铁汁们新年好呀,今天我们来了解自定义函数。 文章目录 1.数学中的函数 2.什么是自定义函数 3.自定义函数如何使用? 4.值传递和引用传递(形参和实参区分) …...
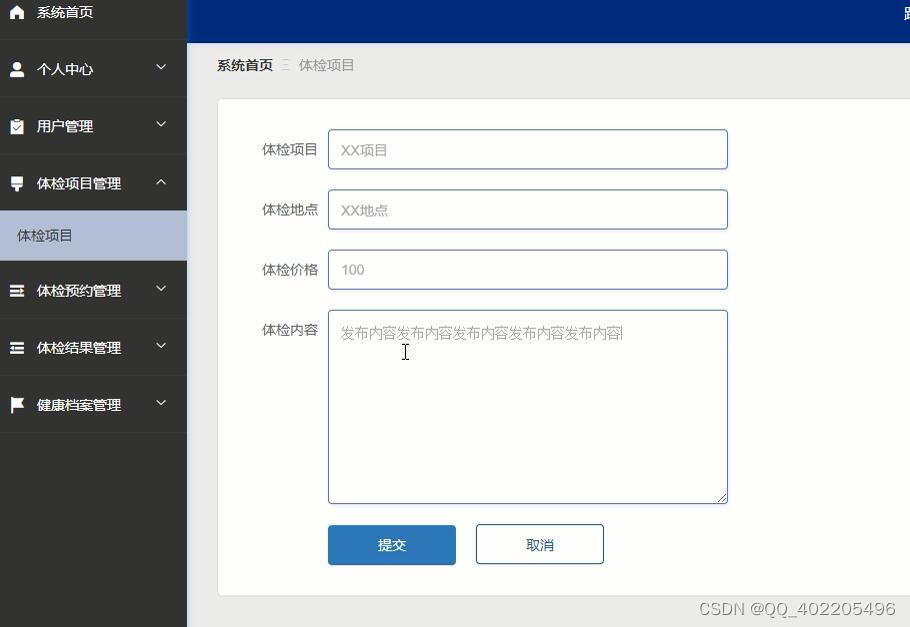
flask+vue+python跨区通勤人员健康体检预约管理系统
跨区通勤人员健康管理系统设计的目的是为用户提供体检项目等功能。 与其它应用程序相比,跨区通勤人员健康的设计主要面向于跨区通勤人员,旨在为管理员和用户提供一个跨区通勤人员健康管理系统。用户可以通过系统及时查看体检预约等。 跨区通勤人员健康管…...

Spring Boot动态加载Jar包与动态配置技术探究
Spring Boot动态加载Jar包与动态配置技术探究 1. 引言 在当今快节奏的软件开发领域,高效的开发框架是保持竞争力的关键。Spring Boot作为一款快速开发框架,以其简化配置、内嵌Web服务器、强大的开发工具等特性,成为众多开发者的首选。其背后…...

Lua metatable metamethod
示例代码 《programming in lua》里有一个案例很详细,就是写一个集合类的table,其负责筛选出table中不重复的元素并组合成一个新的table。本人按照自己的方式默写了一次,结果发现大差不差,代码如下: Set {} --集合--…...
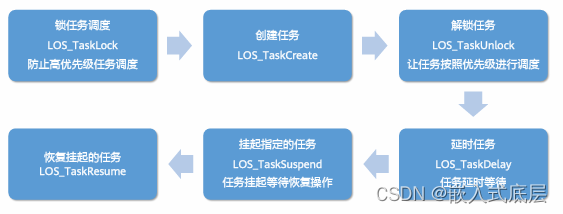
HCIA-HarmonyOS设备开发认证V2.0-3.2.轻量系统内核基础-任务管理
目录 一、任务管理1.1、任务状态1.2、任务基本概念1.3、任务管理使用说明1.4、任务开发流程1.5、任务管理接口 一、任务管理 从系统角度看,任务是竞争系统资源的最小运行单元。任务可以使用或等待CPU、使用内存空间等系统资源,并独立于其它任务运行。 O…...

中小型网络系统总体规划与设计方法
目录 1.基于网络的信息系统基本结构 2.网络需求调研与系统设计原则 3.网络用户调查 4.网络节点地理位置分布情况 5.网络需求详细分析 6.应用概要分析 7.网络工程设计总体目标与设计原则 8.网络结构与拓扑构型设计方法 9.核心层网络结构设计 10.接入核心路由器 11.汇聚…...
以管理员权限删除某文件夹
到开始菜单中找到—命令提示符—右击以管理员运行 使用:del /f /s /q “文件夹位置” 例:del /f /s /q "C:\Program Files (x86)\my_code\.git"...
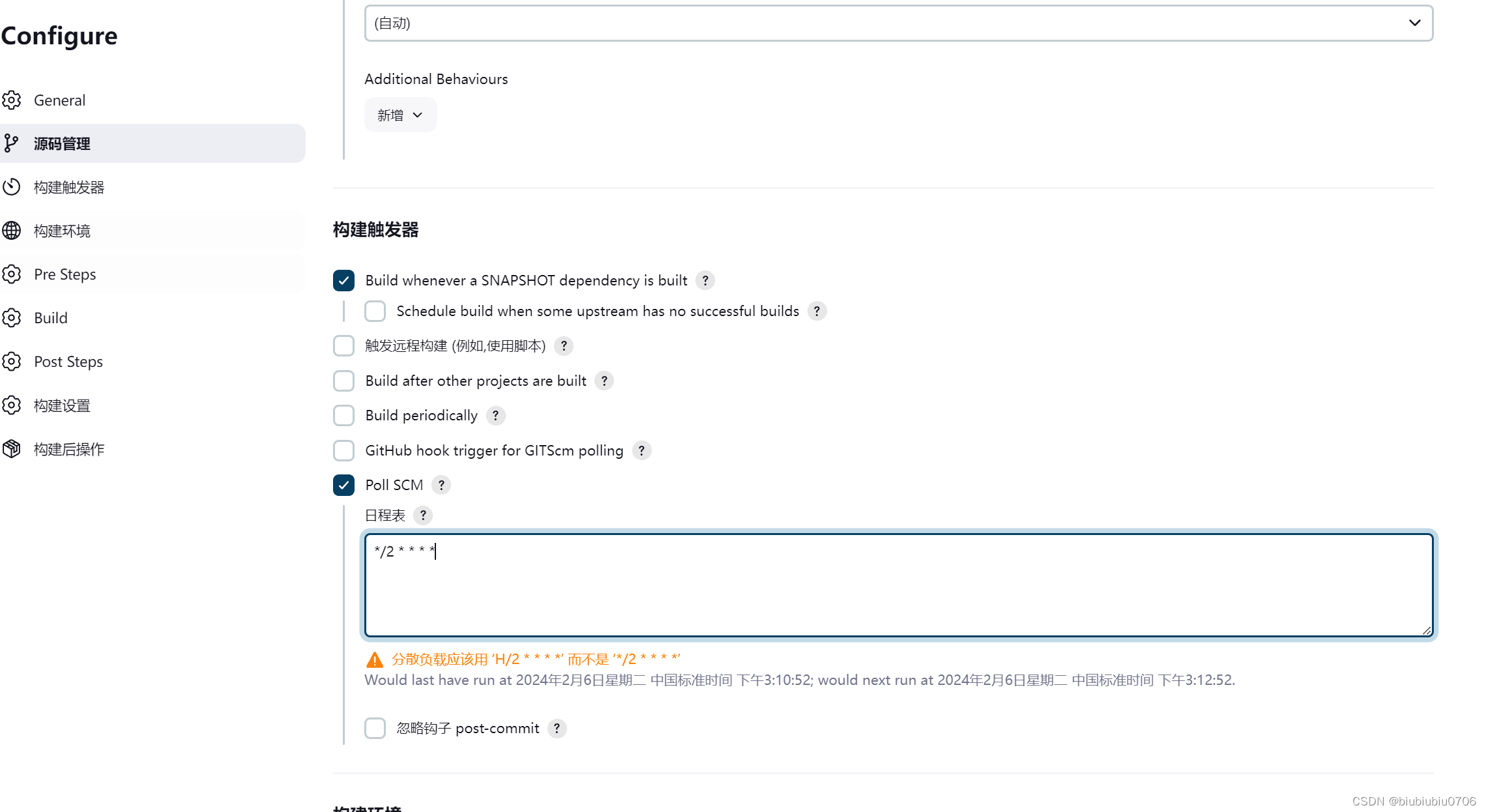
JenkinsGitLab完成自动化构建部署
关于GitLab安装:GitLab安装-CSDN博客 Docker中安装GitLab:Docker下安装GitLab-CSDN博客 安装JenKins Jenkins官网:Jenkins 中文版:Jenkins 安装时候中文页面的war包下不来 在英文页面 记得装JDK8以上 JenKins使用java写的 运行JenKins需要JDK环境 我这里已经装好了 将下…...

JVM 性能调优 - 参数基础(2)
查看 JDK 版本 $ java -version java version "1.8.0_151" Java(TM) SE Runtime Environment (build 1.8.0_151-b12) Java HotSpot(TM) 64-Bit Server VM (build 25.151-b12, mixed mode) 查看 Java 帮助文档 $ java -help 用法: java [-options] class [args...] …...
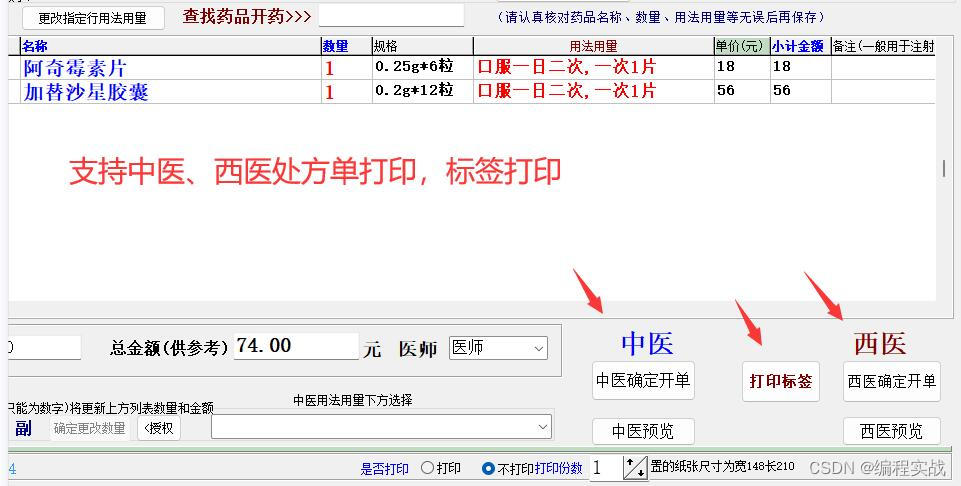
大型软件编程实例分享,诊所门诊处方笺管理系统多台电脑同时使用的软件教程
大型软件编程实例分享,诊所门诊处方笺管理系统多台电脑同时使用的软件教程 一、前言 以下教程以 佳易王诊所门诊电子处方管理系统V17.2 为例说明 软件资源可以点击最下方官网卡片了解详情 软件左侧为导航栏 1、系统参数设置:可以设置打印等参数 2、…...
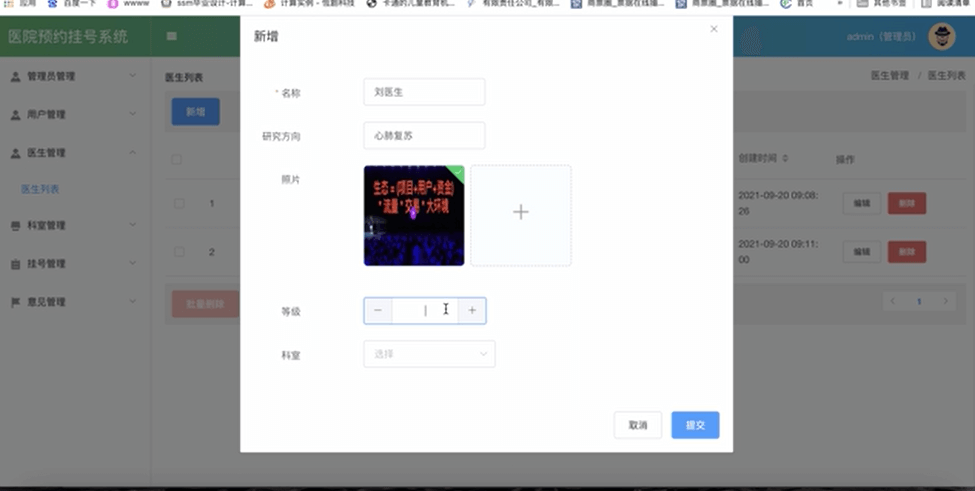
Java基于微信小程序的医院挂号系统
文章目录 1 简介2 技术栈3 系统目标3.2 系统功能需求分析3.2.1 功能需求分析 4 系统模块设计4.1 数据库模块设计 5 系统的实现5.1 微信小程序个人中心5.2 科**室内容查看的实现**5.3 预约挂号的实现5.4 后台管理界面实现5.5 医生预约管理5.6 医生信息管理 参考文献7 推荐阅读8 …...

你是在独立思考,还是在被洗脑?
你有过这样的经历吗? 老板走过来,急匆匆丢给你一句:帮我整理一下那个客户的资料,下午给我。你抬头,应道「好好好」。老板扬长而去。你转念一想: 等等,哪个客户?什么资料?…...
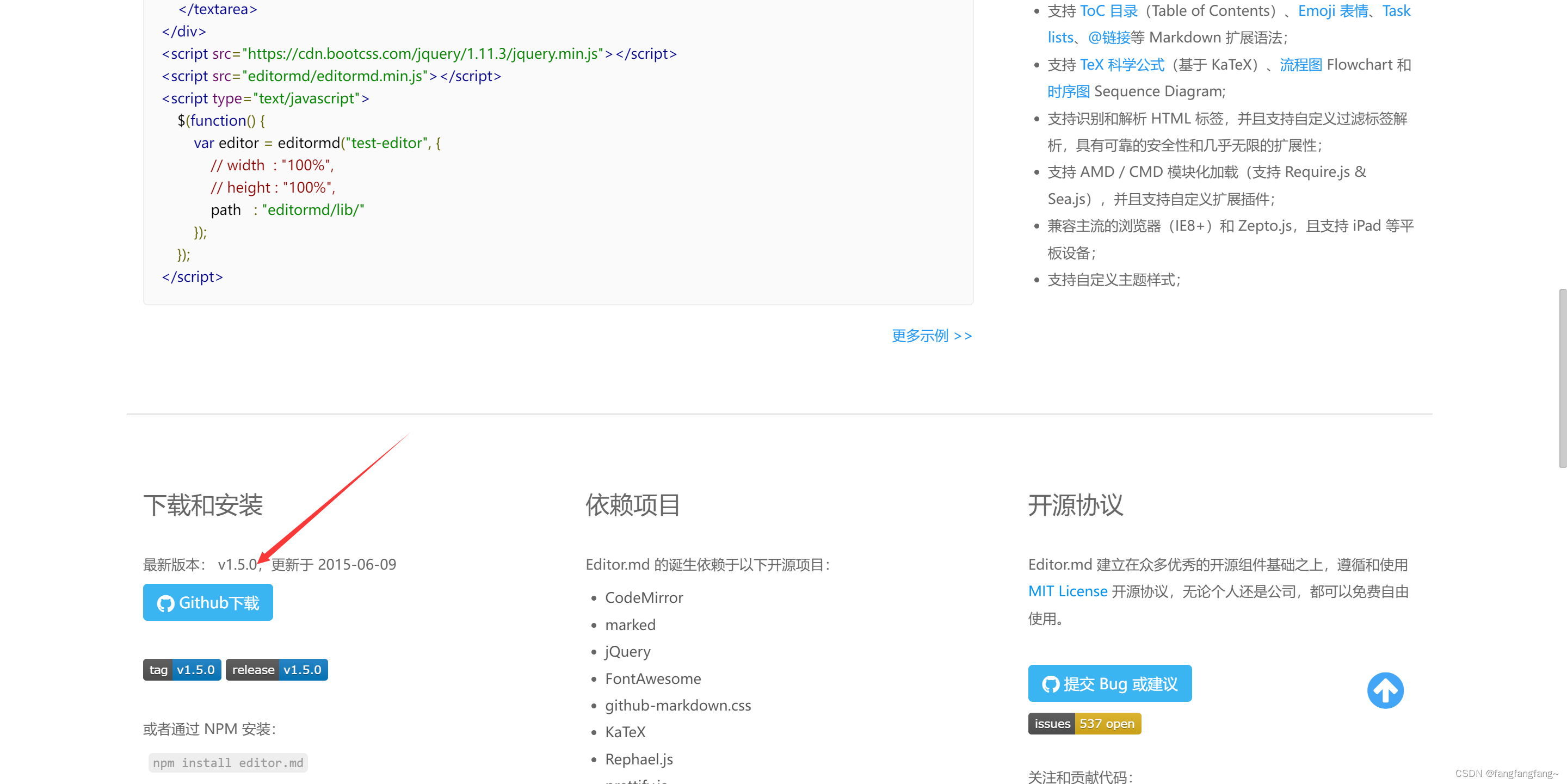
在django中集成markdown文本框
首先需要下载开源组件:http://editor.md.ipandao.com/,可能需要挂梯子。 百度网盘: 链接:https://pan.baidu.com/s/1D9o3P8EQDqSqfhAw10kYkw 提取码:eric 1.在html代码中生成一个div,ideditor <div c…...
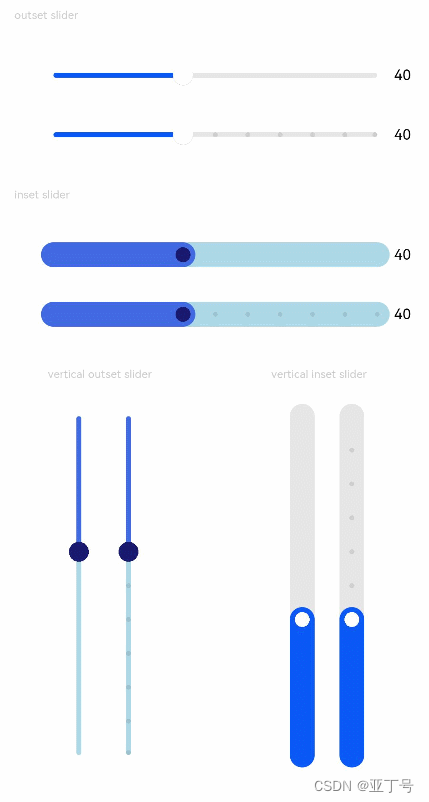
鸿蒙(HarmonyOS)项目方舟框架(ArkUI)之Slider组件
鸿蒙(HarmonyOS)项目方舟框架(ArkUI)之Slider组件 一、操作环境 操作系统: Windows 10 专业版、IDE:DevEco Studio 3.1、SDK:HarmonyOS 3.1 二、Slider组件 滑动条组件,通常用于快速调节设置值,如音量调…...
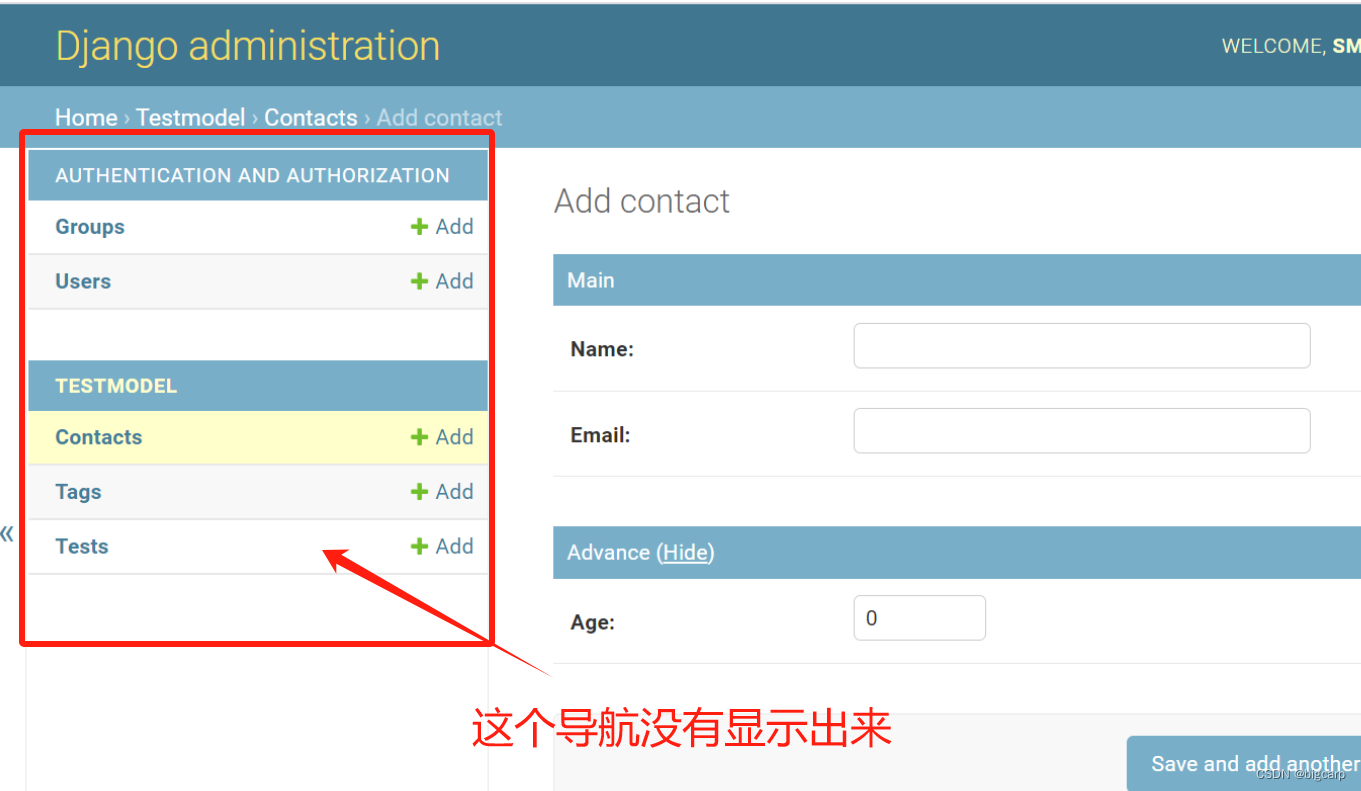
django admin 自定义界面时丢失左侧导航 nav_sidebar
只显示了自定义模板的内容,左侧导航没有显示出来。 原因:context 漏掉了,要补上。 # 错误写法(左侧导航不显示)def changelist_view(self, request, extra_contextNone):form CsvImportForm()payload {"form&qu…...

JSP原理简述
JSP动态网页技术,可以定义html,css,js等静态内容,还可以定义java代码等动态内容。 注意导入坐标时,JSP的scope标签是provided,和servlet一样,否则会报错。 JSP本质上就是一个Servlet,…...

C/C++ - 异常处理
目录 错误处理 异常处理 异常传播 异常规划 标准异常 自定异常 错误处理 在C语言中,错误通常通过函数的返回值来表示。 错误返回值 对于能返回特殊值(如NULL或负值)的函数,在调用时检查这些值来处理错误。 #include <st…...

LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器的上位机配置操作说明
LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器专为工业环境精心打造,完美适配AGV和无人叉车。同时,集成以太网与语音合成技术,为各类高级系统(如MES、调度系统、库位管理、立库等)提供高效便捷的语音交互体验。 L…...

【WiFi帧结构】
文章目录 帧结构MAC头部管理帧 帧结构 Wi-Fi的帧分为三部分组成:MAC头部frame bodyFCS,其中MAC是固定格式的,frame body是可变长度。 MAC头部有frame control,duration,address1,address2,addre…...

边缘计算医疗风险自查APP开发方案
核心目标:在便携设备(智能手表/家用检测仪)部署轻量化疾病预测模型,实现低延迟、隐私安全的实时健康风险评估。 一、技术架构设计 #mermaid-svg-iuNaeeLK2YoFKfao {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg…...

Mybatis逆向工程,动态创建实体类、条件扩展类、Mapper接口、Mapper.xml映射文件
今天呢,博主的学习进度也是步入了Java Mybatis 框架,目前正在逐步杨帆旗航。 那么接下来就给大家出一期有关 Mybatis 逆向工程的教学,希望能对大家有所帮助,也特别欢迎大家指点不足之处,小生很乐意接受正确的建议&…...

关于nvm与node.js
1 安装nvm 安装过程中手动修改 nvm的安装路径, 以及修改 通过nvm安装node后正在使用的node的存放目录【这句话可能难以理解,但接着往下看你就了然了】 2 修改nvm中settings.txt文件配置 nvm安装成功后,通常在该文件中会出现以下配置&…...

pam_env.so模块配置解析
在PAM(Pluggable Authentication Modules)配置中, /etc/pam.d/su 文件相关配置含义如下: 配置解析 auth required pam_env.so1. 字段分解 字段值说明模块类型auth认证类模块,负责验证用户身份&am…...

将对透视变换后的图像使用Otsu进行阈值化,来分离黑色和白色像素。这句话中的Otsu是什么意思?
Otsu 是一种自动阈值化方法,用于将图像分割为前景和背景。它通过最小化图像的类内方差或等价地最大化类间方差来选择最佳阈值。这种方法特别适用于图像的二值化处理,能够自动确定一个阈值,将图像中的像素分为黑色和白色两类。 Otsu 方法的原…...

现代密码学 | 椭圆曲线密码学—附py代码
Elliptic Curve Cryptography 椭圆曲线密码学(ECC)是一种基于有限域上椭圆曲线数学特性的公钥加密技术。其核心原理涉及椭圆曲线的代数性质、离散对数问题以及有限域上的运算。 椭圆曲线密码学是多种数字签名算法的基础,例如椭圆曲线数字签…...

什么?连接服务器也能可视化显示界面?:基于X11 Forwarding + CentOS + MobaXterm实战指南
文章目录 什么是X11?环境准备实战步骤1️⃣ 服务器端配置(CentOS)2️⃣ 客户端配置(MobaXterm)3️⃣ 验证X11 Forwarding4️⃣ 运行自定义GUI程序(Python示例)5️⃣ 成功效果
Python基于历史模拟方法实现投资组合风险管理的VaR与ES模型项目实战
说明:这是一个机器学习实战项目(附带数据代码文档),如需数据代码文档可以直接到文章最后关注获取。 1.项目背景 在金融市场日益复杂和波动加剧的背景下,风险管理成为金融机构和个人投资者关注的核心议题之一。VaR&…...
