Android 车载应用开发之车载操作系统
一、前言
到 2030 年,全球电动汽车的销量将超过 7000 万辆,保有量将达到 3.8 亿辆,全球年度新车渗透率有望触及 60% 。这一数据来自国际能源署(IEA)发布的《全球电动汽车展望2023》。
市场趋势和政策努力的双加持下,新能源汽车来势凶猛,燃油车保有量逐年递减。此番景象让死去的记忆又浮现在你我面前——不久的十年前,智能机以浩浩荡荡之势取代了功能机。相信大家也看到了,为了在此竞争中占有一席之地,传统车厂及近年来如雨后春笋般诞生的”新势力”们把新能源汽车行业卷到了一个新高度。
随着汽车电动化、智能化、网联化的发展,汽车操作系统已经成为车辆中最重要的组成部分之一,车辆的电子化程度决定了车辆的智能化水平、整体性能、安全性与舒适程度。在此背景下又兴起了软件定义汽车的概念,整车企业出于构建软件生态的需要,不断推出新的汽车软件平台,汽车操作系统呈现出百花齐放的发展态势。例如国外电动车智能化先驱特斯拉,国内传统车厂比亚迪、吉利,新势力蔚小理,甚至包括互联网公司华为、阿里等都推出了基于 Linux 或者 Android 等的车用操作系统及配套生态应用。
可见,在这个传统燃油汽车向新能源汽车转型的大浪潮中,车用操作系统的竞争不可谓不激烈。除了传统汽车公司,互联网公司和硬件科技公司也都投入了极大的精力和成本以跻身新能源汽车的赛道。毕竟谁都不想成为浪潮退去过后那个躺在沙滩上的 NOKIA。
在此浪潮中,作为 Android 应用开发者当然也有属于我们自己的小舞台。相比于 2023 年颓势尽显的互联网环境,踏入智能座舱开发领域也未尝不可呢。
二、车载操作系统概述
在智能网联汽车产业大变革趋势下,汽车逐步由传统的交通工具向同时具有交通、娱乐、办公、通信等多种功能的新一代智能移动空间和应用终端迁移。实现能网联功能的驾驶辅助系统
相关文章:

Android 车载应用开发之车载操作系统
一、前言 到 2030 年,全球电动汽车的销量将超过 7000 万辆,保有量将达到 3.8 亿辆,全球年度新车渗透率有望触及 60% 。这一数据来自国际能源署(IEA)发布的《全球电动汽车展望2023》。 市场趋势和政策努力的双加持下,新能源汽车来势凶猛,燃油车保有量逐年递减。此番景象…...
)
Qt PCL学习(文章链接汇总)
Qt PCL学习(一):环境搭建 Qt PCL学习(二):点云读取与保存 Qt PCL学习(三):点云滤波 Qt PCL学习(四):点云关键点 持续更新中…...
安卓动态链接库文件体积优化探索实践
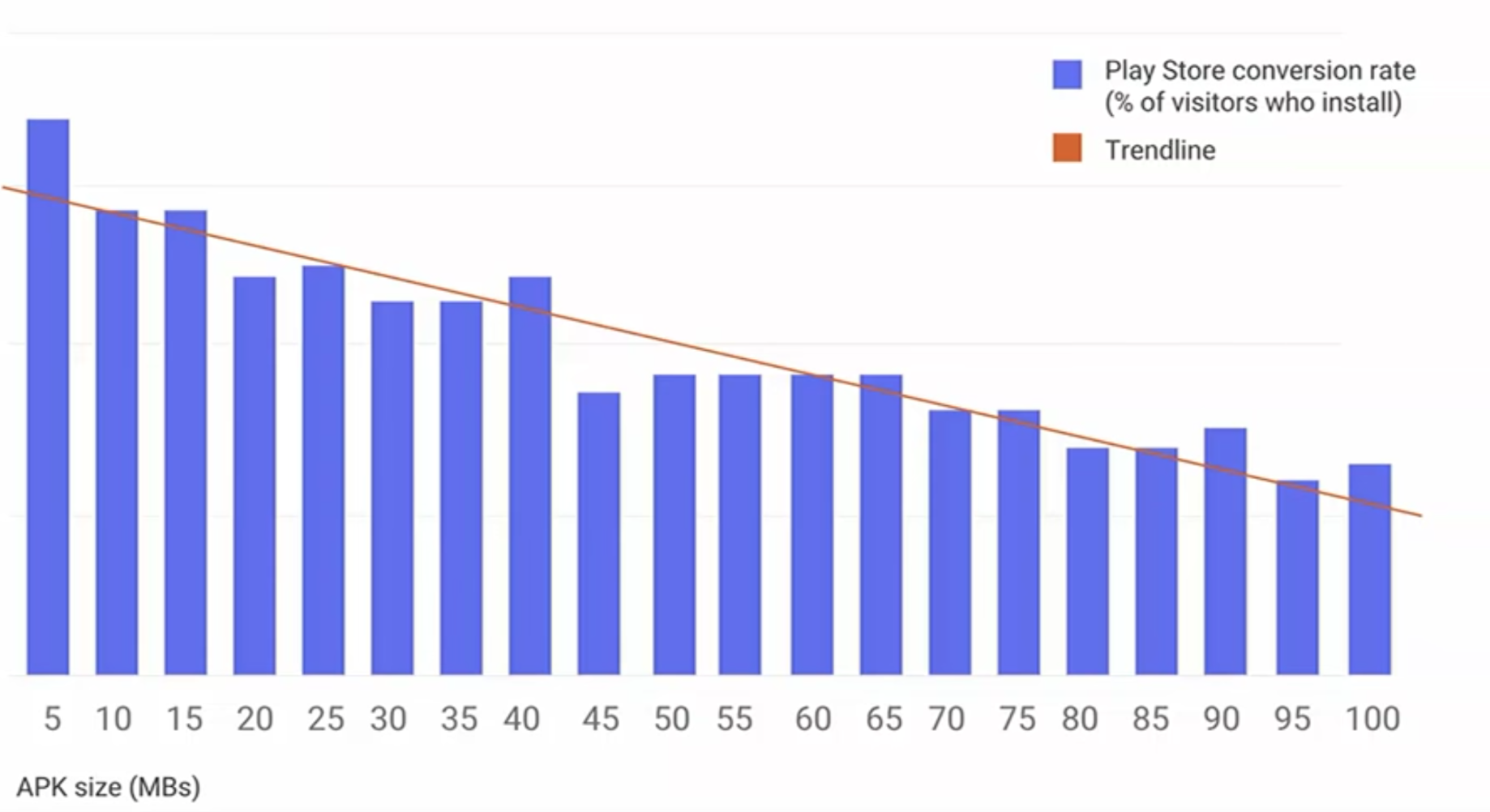
背景介绍 应用安装包的体积影响着用户下载量、安装时长、用户磁盘占用量等多个方面,据Google Play统计,应用体积每增加6MB,安装的转化率将下降1%。 安装包的体积受诸多方面影响,针对dex、资源文件、so文件都有不同的优化策略&…...

[Java][算法 哈希]Day 01---LeetCode 热题 100---01~03
LeetCode 热题 100---01~03 ------->哈希 第一题 两数之和 思路 最直接的理解就是 找出两个数的和等于目标数 这两个数可以相同 但是不能是同一个数字(从数组上理解就是内存上不是同一位置) 解法一:暴力法 暴力解万物 按照需求 …...

【每日一题】LeetCode——链表的中间结点
📚博客主页:爱敲代码的小杨. ✨专栏:《Java SE语法》 | 《数据结构与算法》 | 《C生万物》 ❤️感谢大家点赞👍🏻收藏⭐评论✍🏻,您的三连就是我持续更新的动力❤️ 🙏小杨水平有…...

k8s 部署java应用 基于ingress+jar包
k8 集群ingress的访问模式 先部署一个namespace 命名空间 vim namespace.yaml kind: Namespace apiVersion: v1 metadata:name: ingress-testlabels:env: ingress-test 在部署deployment deployment是pod层一层封装。可以实现多节点部署 资源分配 回滚部署等方式。 部署的…...
深度学习技巧应用36-深度学习模型训练中的超参数调优指南大全,总结相关问题与答案
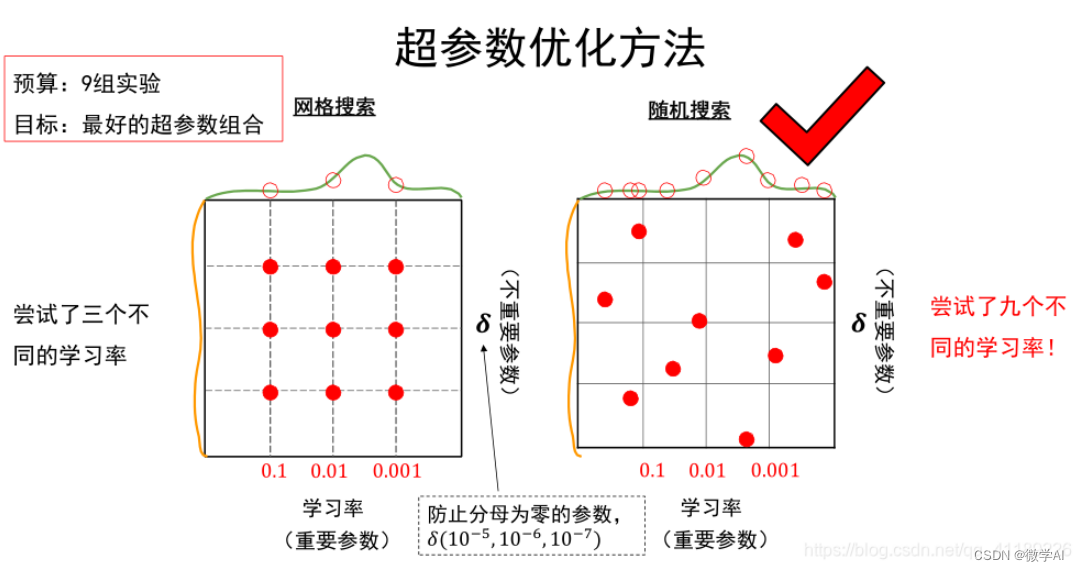
大家好,我是微学AI,今天给大家介绍一下深度学习技巧应用36-深度学习模型训练中的超参数调优指南大全,总结相关问题与答案。深度学习模型训练中的调优指南大全概括了数据预处理、模型架构设计、超参数优化、正则化策略和训练技巧等多个关键方面,以提升模型性能和泛化能力。 …...

“探索AJAX:前端与后端数据交互的利器“
前言 在现代Web开发中,前端与后端之间的数据交互是一个至关重要的环节。为了实现无需刷新页面的动态更新,AJAX(Asynchronous JavaScript and XML)作为一种强大的技术被广泛应用。 AJAX的原理 AJAX通过JavaScript和XMLHttpReque…...

【5G NR】移动通讯中使用的信道编解码技术
目录 一、引言 二、信道编解码技术概述 三、移动通讯中常用的信道编解码技术 四、优缺点分析与比较 五、未来发展趋势 六、结论 本文主要介绍了移动通讯中采用的信道编解码技术,由于在5G NR终端中,通常要兼容4G LTE通讯技术,所以4G LTE…...

用Python Tkinter打造的精彩连连看小游戏【附源码】
文章目录 连连看小游戏:用Python Tkinter打造的精彩游戏体验游戏简介技术背景MainWindow类:职责:方法:Point类: 主执行部分:完整代码:总结: 连连看小游戏:用Python Tkinter打造的精彩游戏体验 在丰富多彩的游戏世界中,…...
nvm安装node后,npm无效
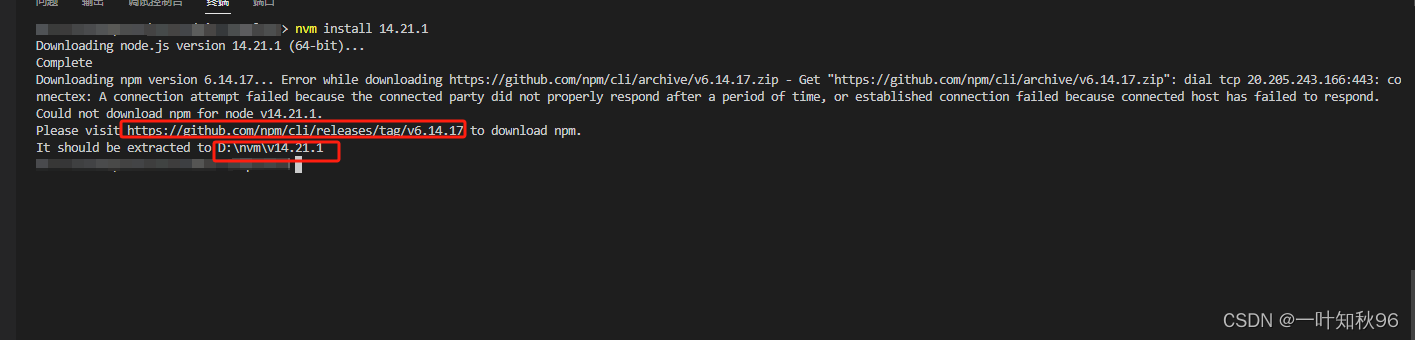
类似报这种问题,是因为去github下载npm时下载失败, Please visit https://github.com/npm/cli/releases/tag/v6.14.17 to download npm. 第一种方法:需要复制这里面的地址爬梯子去下载(github有时不用梯子能直接下载,有…...
spring boot(2.4.x 开始)和spring cloud项目中配置文件application和bootstrap加载顺序
在前面的文章基础上 https://blog.csdn.net/zlpzlpzyd/article/details/136060312 spring boot 2.4.x 版本之前通过 ConfigFileApplicationListener 加载配置 https://github.com/spring-projects/spring-boot/blob/v2.3.12.RELEASE/spring-boot-project/spring-boot/src/mai…...

5-2、S曲线计算【51单片机+L298N步进电机系列教程】
↑↑↑点击上方【目录】,查看本系列全部文章 摘要:本节介绍S曲线的基本变换,将基本形式的S曲线变换成为任意过两点的S曲线,为后续步进电机S曲线运动提供理论支撑 一.计算目标 ①计算经过任意不同两点的S曲线方程 ②可调节曲线平…...

SQL 注入 - http头注入之UA头注入探测
环境准备:构建完善的安全渗透测试环境:推荐工具、资源和下载链接_渗透测试靶机下载-CSDN博客 一、http头注入介绍 HTTP头注入是一种网络安全攻击手段,它利用了Web应用程序对HTTP头的处理不当或缺乏充分的验证和过滤。在这种攻击中,攻击者通过修改HTTP请求头中的某些字段,…...

学习数据结构和算法的第5天
空间复杂度及其常见案例 空间复杂度 空间复杂度也是一个数学函数表达式,是对一个算法在运行过程中临时占用存储空间大小的量度。 空间复杂度不是程序占用了多少bytes的空间,因为这个也没太大意义,所以空间复杂度算的是变量的个数。空间复杂度…...
 root方式)
Android 11 访问 Android/data/或者getExternalCacheDir() root方式
前言: 需求要求安装三方应用ExternalCacheDir()下载下来的apk文件。 getExternalCacheDir() : /storage/emulated/0/Android/data/com../cache/ 获取访问权限 如果手机安卓版本为Android10的时候,可以在AndroidManifest.xml中添加下列代码 android:requestLegacyExt…...
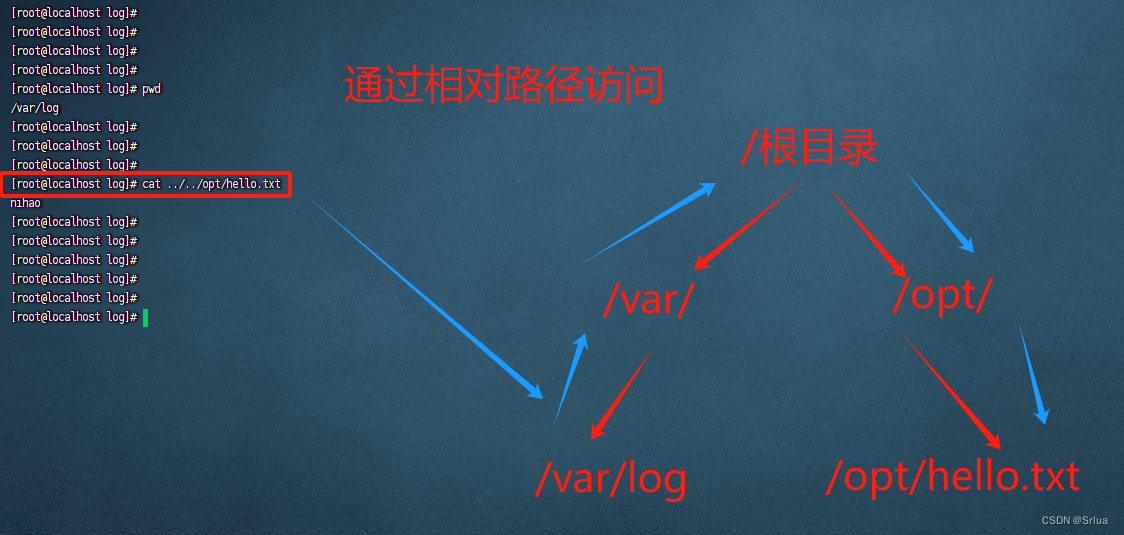
Linux探秘之旅:透彻理解路径、命令与系统概念
目录 如何远程连接 远程登录简明指南 linux区别 1.严格区分大小写 2.linux的命令返回结果判断 3.如何查看网络信息 4.关于后缀名(Linux不关心文件后缀) 4.1 需要记忆的后缀 5.echo命令 6.linux一切皆文件 6.1比如磁盘的文件 6.2可执行文件 …...

哈希算法 c语言
#include <stdio.h> #include <stdlib.h> #include <string.h> // 哈希函数 unsigned int hash_function(const char *str) { unsigned int hash 0; while (*str) { hash (hash * 31 *str) % 1000; str; } return hash;…...

新版MQL语言程序设计:组合模式的原理、应用及代码实现
文章目录 一、什么组合模式二、为什么需要组合模式三、组合模式的实现原理四、组合模式的应用场景五、组合模式的代码实现 一、什么组合模式 组合模式是一种结构型设计模式,它允许将对象组合成树形结构以表示“部分-整体”的层次结构。组合模式使得用户对单个对象和…...
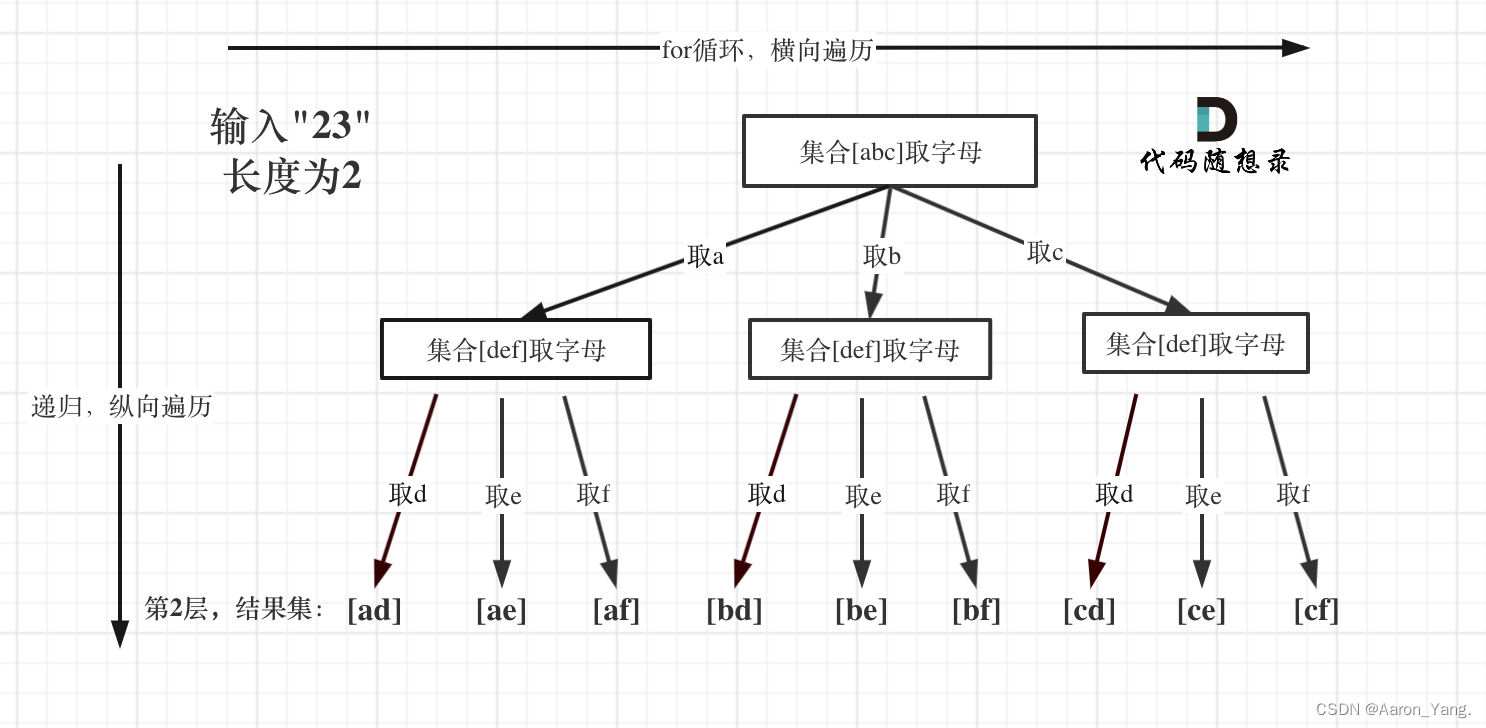
代码随想录算法训练营第25天 | 216.组合总和III ,17.电话号码的字母组合
回溯章节理论基础: https://programmercarl.com/%E5%9B%9E%E6%BA%AF%E7%AE%97%E6%B3%95%E7%90%86%E8%AE%BA%E5%9F%BA%E7%A1%80.html 216.组合总和III 题目链接:https://leetcode.cn/problems/combination-sum-iii/ 思路: 本题就是在[1,2,3,4,5,6,7,…...

conda相比python好处
Conda 作为 Python 的环境和包管理工具,相比原生 Python 生态(如 pip 虚拟环境)有许多独特优势,尤其在多项目管理、依赖处理和跨平台兼容性等方面表现更优。以下是 Conda 的核心好处: 一、一站式环境管理:…...

MFC内存泄露
1、泄露代码示例 void X::SetApplicationBtn() {CMFCRibbonApplicationButton* pBtn GetApplicationButton();// 获取 Ribbon Bar 指针// 创建自定义按钮CCustomRibbonAppButton* pCustomButton new CCustomRibbonAppButton();pCustomButton->SetImage(IDB_BITMAP_Jdp26)…...

unix/linux,sudo,其发展历程详细时间线、由来、历史背景
sudo 的诞生和演化,本身就是一部 Unix/Linux 系统管理哲学变迁的微缩史。来,让我们拨开时间的迷雾,一同探寻 sudo 那波澜壮阔(也颇为实用主义)的发展历程。 历史背景:su的时代与困境 ( 20 世纪 70 年代 - 80 年代初) 在 sudo 出现之前,Unix 系统管理员和需要特权操作的…...

Unit 1 深度强化学习简介
Deep RL Course ——Unit 1 Introduction 从理论和实践层面深入学习深度强化学习。学会使用知名的深度强化学习库,例如 Stable Baselines3、RL Baselines3 Zoo、Sample Factory 和 CleanRL。在独特的环境中训练智能体,比如 SnowballFight、Huggy the Do…...

代理篇12|深入理解 Vite中的Proxy接口代理配置
在前端开发中,常常会遇到 跨域请求接口 的情况。为了解决这个问题,Vite 和 Webpack 都提供了 proxy 代理功能,用于将本地开发请求转发到后端服务器。 什么是代理(proxy)? 代理是在开发过程中,前端项目通过开发服务器,将指定的请求“转发”到真实的后端服务器,从而绕…...

ABAP设计模式之---“简单设计原则(Simple Design)”
“Simple Design”(简单设计)是软件开发中的一个重要理念,倡导以最简单的方式实现软件功能,以确保代码清晰易懂、易维护,并在项目需求变化时能够快速适应。 其核心目标是避免复杂和过度设计,遵循“让事情保…...

AGain DB和倍数增益的关系
我在设置一款索尼CMOS芯片时,Again增益0db变化为6DB,画面的变化只有2倍DN的增益,比如10变为20。 这与dB和线性增益的关系以及传感器处理流程有关。以下是具体原因分析: 1. dB与线性增益的换算关系 6dB对应的理论线性增益应为&…...

STM32标准库-ADC数模转换器
文章目录 一、ADC1.1简介1. 2逐次逼近型ADC1.3ADC框图1.4ADC基本结构1.4.1 信号 “上车点”:输入模块(GPIO、温度、V_REFINT)1.4.2 信号 “调度站”:多路开关1.4.3 信号 “加工厂”:ADC 转换器(规则组 注入…...

Ray框架:分布式AI训练与调参实践
Ray框架:分布式AI训练与调参实践 系统化学习人工智能网站(收藏):https://www.captainbed.cn/flu 文章目录 Ray框架:分布式AI训练与调参实践摘要引言框架架构解析1. 核心组件设计2. 关键技术实现2.1 动态资源调度2.2 …...

Go 并发编程基础:select 多路复用
select 是 Go 并发编程中非常强大的语法结构,它允许程序同时等待多个通道操作的完成,从而实现多路复用机制,是协程调度、超时控制、通道竞争等场景的核心工具。 一、什么是 select select 类似于 switch 语句,但它用于监听多个通…...
