极值图论基础
目录
一,普通子图禁图
二,Turan问题
三,Turan定理、Turan图
1,Turan定理
2,Turan图
四,以完全二部图为禁图的Turan问题
1,最大边数的上界
2,最大边数的下界
五,以偶圈为禁图的Turan问题
六,Ramsey问题
1,Ramsey定理
2,Ramsey问题
一,普通子图禁图
参考普通子图
普通子图禁图指的是,给出一些具体的图,描述某个图不以这些具体的图作为普通子图。
二,Turan问题
给出一个图集F,求以F为普通子图禁图的图的最大边数,以及取到最大值的图是什么?
即,一个图最多能有多少条边,使得不以F中的任意图为普通子图。
PS:我们只关心简单图,否则如果2个点之间连无穷条多重边,那就没意义了。
PS:取到最大值的图称为极图,如果有唯一的极图,我们就说满足条件的极图是什么,不需要赘述边数了。
三,Turan定理、Turan图
1,Turan定理
以完全图K(r+1)为禁图的极图是平衡完全r部图,且没有其他极图。
2,Turan图
n个点的平衡完全r部图也叫图兰图Tr,n,即把n个点平均分成r份得到的完全r部图。
所以也可以说以完全图K(r+1)为禁图的n个点的图,唯一的极图是图兰图Tr,n。
比如,以完全图K4为禁图的8个点的图,唯一的极图是T3,8:
实际上,图兰图Tr,n的边数就是,其中p=n/r
比如T3,8,n=8,r=3,p=2,
四,以完全二部图为禁图的Turan问题
1,最大边数的上界
定理:对于任意s>=t>=2,存在常数C,对于任意n,以完全二部图Ks,t为禁图的图的边数不超过
猜想:对于任意s>=t>=2,以完全二部图Ks,t为禁图的图的最大边数为
其中,θ是渐进相等的符号。
2,最大边数的下界
存在常数C,对于任意t>=2,任意s>C^t,以完全二部图Ks,t为禁图的图的最大边数为
已经很接近上面的猜想了,但还没完全解决。
五,以偶圈为禁图的Turan问题
定理:对于任意k>=2,以2k个点构成的偶圈为禁图的图的边数不超过
猜想:对于任意k>=2,以2k个点构成的偶圈为禁图的图的边数为
六,Ramsey问题
1,Ramsey定理
对于任意的s>1,t>1,一定存在一个整数N,对于任意N个点的图,要么存在s个点两两相连,要么存在t个点两两不相连。
我们把满足条件的最小N记做R(s,t)
2,Ramsey问题
Ramsey问题就是R(s,t)的大小和性质。
相关文章:
极值图论基础
目录 一,普通子图禁图 二,Turan问题 三,Turan定理、Turan图 1,Turan定理 2,Turan图 四,以完全二部图为禁图的Turan问题 1,最大边数的上界 2,最大边数的下界 五,…...

word导出链接
java 使用 POI 操作 XWPFDocumen 创建和读取 Office Word 文档基础篇 https://www.cnblogs.com/mh-study/p/9747945.html word标签解析文档 http://www.datypic.com/sc/ooxml/e-w_tbl-1.html...
 Object Pascal 学习笔记---第4章第2.5节(重载和模糊调用))
(delphi11最新学习资料) Object Pascal 学习笔记---第4章第2.5节(重载和模糊调用)
4.2.5 重载和模糊调用 当调用一个重载的函数时,编译器通常会找到匹配的版本并正确工作,或者如果没有任何重载版本具有正确匹配的参数(正如我们刚刚看到的),则会报出错误。 但还有第三种情况:假设编…...
ElementUI Data:Table 表格
ElementUI安装与使用指南 Table 表格 点击下载learnelementuispringboot项目源码 效果图 el-table.vue(Table表格)页面效果图 项目里el-table.vue代码 <script> export default {name: el_table,data() {return {tableData: …...

11.2 OpenGL可编程顶点处理:细分着色器
细分 Tessellation Tessellation(细分)是计算机图形学中的一种技术,用于在渲染过程中提高模型表面的几何细节。它通过在原始图元(如三角形、四边形或补丁)之间插入新的顶点和边,对图元进行细化分割&#x…...

微软正在偷走你的浏览记录,Edge浏览器偷疯了
虽然现在 Edge 浏览器相当强大,甚至在某种程度上更符合中国用户的使用体验;但最近新的Edge浏览器推出后一直在使用的用户应该有感受到,原本的冰清玉洁的转校生慢慢小鸡脚藏不住了,广告越来越多,越来越流氓了。 电脑之前…...
)
什么是数据库软删除,什么场景下要用软删除?(go GORM硬删除)
文章目录 什么是数据库软删除,什么场景下要用软删除?go GORM硬删除什么是数据库软删除什么场景下要用软删除 什么是数据库软删除,什么场景下要用软删除? go GORM硬删除 使用的是 GORM,默认启用了软删除功能ÿ…...
计算机设计大赛 深度学习+python+opencv实现动物识别 - 图像识别
文章目录 0 前言1 课题背景2 实现效果3 卷积神经网络3.1卷积层3.2 池化层3.3 激活函数:3.4 全连接层3.5 使用tensorflow中keras模块实现卷积神经网络 4 inception_v3网络5 最后 0 前言 🔥 优质竞赛项目系列,今天要分享的是 🚩 *…...

我主编的电子技术实验手册(02)——仪表与电源
本专栏是笔者主编教材(图0所示)的电子版,依托简易的元器件和仪表安排了30多个实验,主要面向经费不太充足的中高职院校。每个实验都安排了必不可少的【预习知识】,精心设计的【实验步骤】,全面丰富的【思考习…...

C语言----内存函数
内存函数主要用于动态分配和管理内存,它直接从指针的方位上进行操作,可以实现字节单位的操作。 其包含的头文件都是:string.h memcpy copy block of memory的缩写----拷贝内存块 格式: void *memcpy(void *dest, const void …...

【力扣】快乐数,哈希集合 + 快慢指针 + 数学
快乐数原题地址 方法一:哈希集合 定义函数 getNext(n) ,返回 n 的所有位的平方和。一直执行 ngetNext(n) ,最终只有 2 种可能: n 停留在 1 。无限循环且不为 1 。 证明:情况 1 是存在的,如力扣的示例一…...

c实现顺序表
目录 c语言实现顺序表 完整代码实现 c语言实现顺序表 顺序表的结构定义: typedef struct vector {int size; // 顺序表的容量int count; // 顺序表现在存储了多少个数据int *data; // 指针指向连续的整型存储空间 } vector;顺序表的结构操作: 1、初始…...

微软为新闻编辑行业推出 AI 辅助项目,记者参加免费课程
2 月 6 日消息,微软当地时间 5 日发布新闻稿宣布与多家新闻机构展开多项基于生成式 AI 的合作。微软表示,其使命是确保新闻编辑室在今年和未来拥有创新。 目前建议企业通过微软官方合作伙伴获取服务,可以合规、稳定地提供企业用户使用ChatGP…...
openssl3.2 - exp - buffer to BIO
文章目录 openssl3.2 - exp - buffer to BIO概述笔记END openssl3.2 - exp - buffer to BIO 概述 openssl的资料看的差不多了, 准备将工程中用到的知识点整理一下. openssl中很多API是以操作文件作为输入的, 也有很多API是以BIO作为输入的. 不管文件是不是受保护的, 如果有可…...

Android 13.0 系统framework修改低电量关机值为3%
1、讲在最前面 系统rom定制开发中,其中在低电量时,系统会自动关机,这个和不同的平台和底层驱动和硬件都有关系,需要结合这些来实际调整这个值,我们可以通过分析源码中电池服务的代码,然后进行修改如何实现…...
【EAI 013】BC-Z: Zero-Shot Task Generalization with Robotic Imitation Learning
论文标题:BC-Z: Zero-Shot Task Generalization with Robotic Imitation Learning 论文作者:Eric Jang, Alex Irpan, Mohi Khansari, Daniel Kappler, Frederik Ebert, Corey Lynch, Sergey Levine, Chelsea Finn 论文原文:https://arxiv.org…...

一文讲透ast.literal_eval() eval() json.loads()
文章目录 一文讲透ast.literal_eval() eval() json.loads()1. ast.literal_eval()2. eval()3. json.loads()4. 总结 一文讲透ast.literal_eval() eval() json.loads() 在Python库中,我们经常会遇到需要将字符串转换为相应对象或数据结构的情况。在这种情况下&#…...

微软.NET6开发的C#特性——类、结构体和联合体
我是荔园微风,作为一名在IT界整整25年的老兵,看到不少初学者在学习编程语言的过程中如此的痛苦,我决定做点什么,下面我就重点讲讲微软.NET6开发人员需要知道的C#特性,然后比较其他各种语言进行认识。 C#经历了多年发展…...
naiveui 上传图片遇到的坑 Upload
我在开发图片上传功能, 需要手动触发上传 但是我调用它内部自定义submit方法, 结果接口一直在报错400 我反反复复的测试了好就, 确定了就是我前端的问题,因为之前一直在做后端的错误排查, 以为是编译问题(因为之前也出现过这个问题) 好 , 我把其中一个参数类型改为String类型, …...
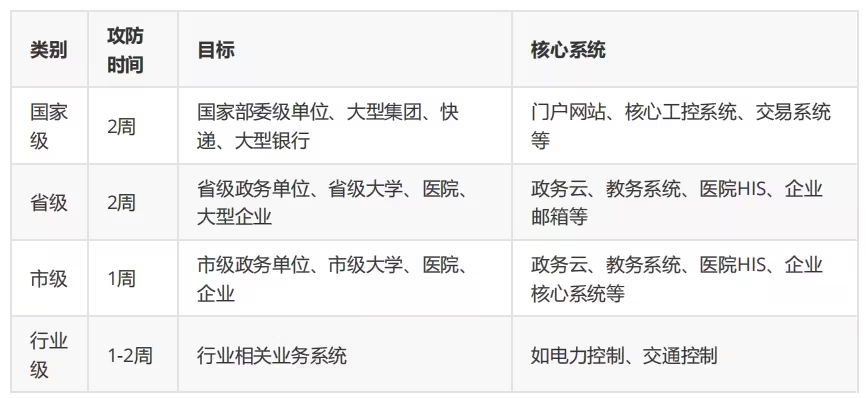
安全之护网(HVV)、红蓝对抗
文章目录 红蓝对抗什么是护网行动?护网分类护网的时间 什么是红蓝对抗红蓝对抗演练的目的什么是企业红蓝对抗红蓝对抗价值参考 红蓝对抗 什么是护网行动? 护网的定义是以国家组织组织事业单位、国企单位、名企单位等开展攻防两方的网络安全演习。进攻方…...

渲染学进阶内容——模型
最近在写模组的时候发现渲染器里面离不开模型的定义,在渲染的第二篇文章中简单的讲解了一下关于模型部分的内容,其实不管是方块还是方块实体,都离不开模型的内容 🧱 一、CubeListBuilder 功能解析 CubeListBuilder 是 Minecraft Java 版模型系统的核心构建器,用于动态创…...

linux arm系统烧录
1、打开瑞芯微程序 2、按住linux arm 的 recover按键 插入电源 3、当瑞芯微检测到有设备 4、松开recover按键 5、选择升级固件 6、点击固件选择本地刷机的linux arm 镜像 7、点击升级 (忘了有没有这步了 估计有) 刷机程序 和 镜像 就不提供了。要刷的时…...

解决本地部署 SmolVLM2 大语言模型运行 flash-attn 报错
出现的问题 安装 flash-attn 会一直卡在 build 那一步或者运行报错 解决办法 是因为你安装的 flash-attn 版本没有对应上,所以报错,到 https://github.com/Dao-AILab/flash-attention/releases 下载对应版本,cu、torch、cp 的版本一定要对…...

CRMEB 框架中 PHP 上传扩展开发:涵盖本地上传及阿里云 OSS、腾讯云 COS、七牛云
目前已有本地上传、阿里云OSS上传、腾讯云COS上传、七牛云上传扩展 扩展入口文件 文件目录 crmeb\services\upload\Upload.php namespace crmeb\services\upload;use crmeb\basic\BaseManager; use think\facade\Config;/*** Class Upload* package crmeb\services\upload* …...

Springboot社区养老保险系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,社区养老保险系统小程序被用户普遍使用,为方…...

云原生安全实战:API网关Kong的鉴权与限流详解
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 一、基础概念 1. API网关(API Gateway) API网关是微服务架构中的核心组件,负责统一管理所有API的流量入口。它像一座…...

搭建DNS域名解析服务器(正向解析资源文件)
正向解析资源文件 1)准备工作 服务端及客户端都关闭安全软件 [rootlocalhost ~]# systemctl stop firewalld [rootlocalhost ~]# setenforce 0 2)服务端安装软件:bind 1.配置yum源 [rootlocalhost ~]# cat /etc/yum.repos.d/base.repo [Base…...

scikit-learn机器学习
# 同时添加如下代码, 这样每次环境(kernel)启动的时候只要运行下方代码即可: # Also add the following code, # so that every time the environment (kernel) starts, # just run the following code: import sys sys.path.append(/home/aistudio/external-libraries)机…...

多模态图像修复系统:基于深度学习的图片修复实现
多模态图像修复系统:基于深度学习的图片修复实现 1. 系统概述 本系统使用多模态大模型(Stable Diffusion Inpainting)实现图像修复功能,结合文本描述和图片输入,对指定区域进行内容修复。系统包含完整的数据处理、模型训练、推理部署流程。 import torch import numpy …...

逻辑回归暴力训练预测金融欺诈
简述 「使用逻辑回归暴力预测金融欺诈,并不断增加特征维度持续测试」的做法,体现了一种逐步建模与迭代验证的实验思路,在金融欺诈检测中非常有价值,本文作为一篇回顾性记录了早年间公司给某行做反欺诈预测用到的技术和思路。百度…...
