【动态规划】【中位数】【C++算法】1478. 安排邮筒
# 作者推荐
【深度优先搜索】【树】【图论】2973. 树中每个节点放置的金币数目
本文涉及知识点
动态规划汇总
LeetCode1478. 安排邮筒
给你一个房屋数组houses 和一个整数 k ,其中 houses[i] 是第 i 栋房子在一条街上的位置,现需要在这条街上安排 k 个邮筒。
请你返回每栋房子与离它最近的邮筒之间的距离的 最小 总和。
答案保证在 32 位有符号整数范围以内。
示例 1:
输入:houses = [1,4,8,10,20], k = 3
输出:5
解释:将邮筒分别安放在位置 3, 9 和 20 处。
每个房子到最近邮筒的距离和为 |3-1| + |4-3| + |9-8| + |10-9| + |20-20| = 5 。
示例 2:
输入:houses = [2,3,5,12,18], k = 2
输出:9
解释:将邮筒分别安放在位置 3 和 14 处。
每个房子到最近邮筒距离和为 |2-3| + |3-3| + |5-3| + |12-14| + |18-14| = 9 。
示例 3:
输入:houses = [7,4,6,1], k = 1
输出:8
示例 4:
输入:houses = [3,6,14,10], k = 4
输出:0
提示:
n == houses.length
1 <= n <= 100
1 <= houses[i] <= 104
1 <= k <= n
数组 houses 中的整数互不相同。
动态规划
原理
houser[i,j]之间安装邮筒,安装到正中间的房子是最优解。
a,假定房子数是奇数,假定共有2n+1个房子。假定左边有i1个房子,右边有i2个房子。如果i1 < i2,则右移可以缩短距离;i1 > i2,则左移可以缩短距离。如果邮筒不在屋子上,则i1永远不会等于i2。i1==i2,则必定在最中间的屋子。i+(j-i)/2。
b,屋子为偶数,在中间的两坐房子之间,才会让i1和i2。其实中间两间房子的任何一间房子都可以。
可以统一为:i+(j-i)/2
确切的说: { 左边及本身的房子数小于右边的房子数,右移动。 右边及本身的房子数小于左边的房子数,左移动。 \begin{cases} 左边及本身的房子数小于右边的房子数,右移动。\\ 右边及本身的房子数小于左边的房子数,左移动。\\ \end{cases} {左边及本身的房子数小于右边的房子数,右移动。右边及本身的房子数小于左边的房子数,左移动。 → \rightarrow → 稳定状态下,必须
{ i 1 > = i 2 , i 1 < = i 2 → i 1 = = i 2 邮筒不在房子上 i 1 + 1 > = i 2 , i 2 + 1 > = i 1 → a b s ( i 1 − i 2 ) < = 1 邮筒在房子上 → \begin{cases} i1 >=i2,i1 <=i2 \rightarrow i1==i2 & 邮筒不在房子上 \\ i1+1>=i2,i2+1 >= i1 \rightarrow abs(i1-i2)<=1 & 邮筒在房子上\\ \end{cases} \rightarrow {i1>=i2,i1<=i2→i1==i2i1+1>=i2,i2+1>=i1→abs(i1−i2)<=1邮筒不在房子上邮筒在房子上→
如果房子数量是奇数
{ 邮筒不在房子上 i 1 = = i 2 → ( i 1 + i 2 ) 是偶数 → 房子总数是奇数矛盾 邮筒在房子上且 i 1 等于 i 2 正中间的房子 邮筒在房子上且 i 1 和 i 2 相差 1 假定 11 + 1 = i 2 → i 1 + i 2 + 1 是偶数,和总数是奇数矛盾 → \begin{cases} 邮筒不在房子上& i1==i2 \rightarrow (i1+i2)是偶数 \rightarrow 房子总数是奇数矛盾 \\ 邮筒在房子上且i1等于i2 & 正中间的房子 \\ 邮筒在房子上且i1和i2相差1 & 假定11+1=i2 \rightarrow i1+i2+1是偶数,和总数是奇数矛盾 \\ \end{cases} \rightarrow ⎩ ⎨ ⎧邮筒不在房子上邮筒在房子上且i1等于i2邮筒在房子上且i1和i2相差1i1==i2→(i1+i2)是偶数→房子总数是奇数矛盾正中间的房子假定11+1=i2→i1+i2+1是偶数,和总数是奇数矛盾→ 如果房子的数量是奇数则只能安装在最中间。
如果房子数量是偶数
{ 邮筒不在房子上 i 1 = = i 2 → 中间两间房子的空地 邮筒在房子上且 i 1 等于 i 2 i 1 + i 2 + 1 是奇数,与假设矛盾 邮筒在房子上且 i 1 和 i 2 相差 1 中间任意两间房子 → \begin{cases} 邮筒不在房子上& i1==i2 \rightarrow 中间两间房子的空地 \\ 邮筒在房子上且i1等于i2 & i1+i2+1是奇数,与假设矛盾 \\ 邮筒在房子上且i1和i2相差1 & 中间任意两间房子 \\ \end{cases} \rightarrow ⎩ ⎨ ⎧邮筒不在房子上邮筒在房子上且i1等于i2邮筒在房子上且i1和i2相差1i1==i2→中间两间房子的空地i1+i2+1是奇数,与假设矛盾中间任意两间房子→
如果房间数是偶数,则中间的两间房子及之间的空地都是最优解。
预处理
vDis[i][j] ,记录一个邮筒到house[i,j]的距离之和。houses要先排序。
动态规划的状态表示
dp[i][j] 表示 j个邮筒支持前i栋房最小距离。
动态规划的状态方程
通过前者状态更新后置状态。
k = 1 i + k < = h o u s e s . l e n g t h \Large_{k=1}^{i+k <= houses.length} k=1i+k<=houses.length pre[i+k][j+1] = min( ⋯ \cdots ⋯,pre[i][j]+vDis[ ⋯ \cdots ⋯])
动态规划的初始值
dp[0][0]=0 ,其它INT_MAX,表示非法值。
动态规划的填表顺序
i从小到大,j从小到大。
动态规划的返回值
dp.back()[k]
代码
核心代码
class Solution {
public:int minDistance(vector<int>& houses, int K) {m_c = houses.size();sort(houses.begin(), houses.end());vector<vector<int>> vDis(m_c, vector<int>(m_c));for (int center = 0; center < m_c; center++){{int iDis = 0;for (int i = center, j = center; (i >= 0) && (j < m_c); i--, j++){iDis += houses[j] - houses[i];vDis[i][j] = iDis;}}{int iDis = 0;for (int i = center, j = center + 1; (i >= 0) && (j < m_c); i--, j++){iDis += houses[j] - houses[i];vDis[i][j] = iDis;}}}vector<vector<int>> dp(m_c + 1, vector<int>(K + 1, INT_MAX));dp[0][0] = 0;for (int i = 0; i <= m_c; i++){for (int j = 0; j < K; j++){if (INT_MAX == dp[i][j]){continue;}for (int m = 1; m + i <= m_c; m++){dp[m + i][j + 1] = min(dp[m + i][j + 1],dp[i][j]+vDis[i][i+m-1]);}}}return dp.back().back();}int m_c;
};
测试用例
template<class T>
void Assert(const T& t1, const T& t2)
{assert(t1 == t2);
}template<class T>
void Assert(const vector<T>& v1, const vector<T>& v2)
{if (v1.size() != v2.size()){assert(false);return;}for (int i = 0; i < v1.size(); i++){Assert(v1[i], v2[i]);}}int main()
{ vector<int> houses;int k;{Solution sln;houses = { 7,4,6,1 };k = 1;auto res = sln.minDistance(houses, k);Assert(8, res);}{Solution sln;houses = { 1, 4, 8, 10, 20 };k = 3;auto res = sln.minDistance(houses, k);Assert(5, res);}{Solution sln;houses = { 2,3,5,12,18 };k = 2;auto res = sln.minDistance(houses, k);Assert(9, res);}{Solution sln;houses = { 3,6,14,10 };k = 4;auto res = sln.minDistance(houses, k);Assert(0, res);}
}
2023年2月版
class Solution {
public:
int minDistance(vector& houses, int k) {
const int iNotMay = 1000 * 1000 * 10;
std::sort(houses.begin(), houses.end());
m_c = houses.size();
vector pre(m_c);
for (int i = 0; i < m_c; i++)
{
pre[i] = Cost(houses, 0, i + 1);
}
for (int iK = 2; iK <= k; iK++)
{
vector dp(m_c, iNotMay);
for (int iHouse = 0; iHouse < houses.size(); iHouse++)
{
for (int pr = 0; pr < iHouse; pr++)
{
if (iNotMay == pre[pr])
{
continue;
}
dp[iHouse] = min(dp[iHouse], pre[pr] + Cost(houses, pr+1, iHouse + 1));
}
}
pre.swap(dp);
}
return pre.back();
}
int Cost(const vector& houses,int left, int r)
{
int iCost = 0;
int iMean = houses[left + (r - left) / 2];
for (int i = left; i < r; i++)
{
iCost += abs(houses[i] - iMean);
}
return iCost;
}
int m_c;
};
2023年7月版
class Solution {
public:
int minDistance(vector& houses, int k) {
m_c = houses.size();
sort(houses.begin(), houses.end());
vector<vector> vCost(m_c, vector(m_c));
for(int i= 0 ;i < m_c; i++ )
for (int j = i+1; j < m_c; j++)
{
int iMidValue = houses[i] + (houses[j] - houses[i]) / 2;
int cost = 0;
int k = i+1;
for (; houses[k] <= iMidValue; k++)
{
cost += houses[k] - houses[i];
}
for (; k < j; k++)
{
cost += houses[j] - houses[k];
}
vCost[i][j] = cost;
}
const int iNotMay = 1000 * 1000 * 10;
vector<vector> dp(m_c + 1, vector(k + 1, iNotMay));
dp[0][0] = 0;
dp[0][1] = 0;
vector vBegin(m_c);
{
int iSum = 0;
for (int i = 1; i < m_c; i++)
{
iSum += (houses[i] - houses[i - 1]) * i;
vBegin[i] = iSum;
}
}
for (int i = 1; i < m_c; i++)
{
for (int prePos = 0; prePos < i; prePos++)
{
for (int preK = 0; preK < k; preK++)
{
if (iNotMay == dp[prePos][preK])
{
continue;
}
if (0 == preK)
{
dp[i][preK + 1] = vBegin[i];
continue;
}
dp[i][preK + 1] = min(dp[i][preK + 1],dp[prePos][preK] + vCost[prePos][i]);
}
}
}
vector vEnd(m_c);
{
int iSum = 0;
for (int i = m_c - 2; i >= 0; i–)
{
iSum += (houses[i + 1] - houses[i]) * (m_c - 1 - i);
vEnd[i] = iSum;
}
}
int iRet = iNotMay;
for (int i = k-1; i < m_c; i++)
{
iRet = min(iRet, dp[i][k] +vEnd[i]);
}
return iRet;
}
int m_c;
};

扩展阅读
视频课程
有效学习:明确的目标 及时的反馈 拉伸区(难度合适),可以先学简单的课程,请移步CSDN学院,听白银讲师(也就是鄙人)的讲解。
https://edu.csdn.net/course/detail/38771
如何你想快
速形成战斗了,为老板分忧,请学习C#入职培训、C++入职培训等课程
https://edu.csdn.net/lecturer/6176
相关下载
想高屋建瓴的学习算法,请下载《喜缺全书算法册》doc版
https://download.csdn.net/download/he_zhidan/88348653
| 我想对大家说的话 |
|---|
| 闻缺陷则喜是一个美好的愿望,早发现问题,早修改问题,给老板节约钱。 |
| 子墨子言之:事无终始,无务多业。也就是我们常说的专业的人做专业的事。 |
| 如果程序是一条龙,那算法就是他的是睛 |
测试环境
操作系统:win7 开发环境: VS2019 C++17
或者 操作系统:win10 开发环境: VS2022 C++17
如无特殊说明,本算法用**C++**实现。

相关文章:

【动态规划】【中位数】【C++算法】1478. 安排邮筒
# 作者推荐 【深度优先搜索】【树】【图论】2973. 树中每个节点放置的金币数目 本文涉及知识点 动态规划汇总 LeetCode1478. 安排邮筒 给你一个房屋数组houses 和一个整数 k ,其中 houses[i] 是第 i 栋房子在一条街上的位置,现需要在这条街上安排 k…...
)
C#系列-数据结构+递归算法+排序算法(3)
C#数据结构 在C#中,数据结构是用于组织和管理数据的方式,以便更有效地进行数据的存储、访问和操作。数据结构对于算法的性能和设计至关重要,因为它们决定了数据如何在内存中布局以及如何与算法进行交互。C#提供了许多内置的数据结构…...

Redis实现秒杀
前期准备 缓存选择考虑 Redis和Redis Cluster(分布式版本),是一个分布式缓存系统。其支持多种数据结构,也支持MQ。Redis在性能上做了大量优化。因此使用Redis或者Redis Cluster就可以轻松实现一个强大的秒杀系统。 用Redis的这…...

4 scala集合-Map
和 Java 一样,Scala 也有表示键值对(Key-Value)集合的 Map 数据结构。同样,Map 也分不可变和可变,不可变需要使用类 scala.collection.mutable.Map。 1 不可变 Map 可以使用以下语法定义不可变 Map 对象 val/var ma…...

QT 对象树模型
QObject是Qt里边绝大部分类的根类 QObject对象之间是以对象树的形式组织起来的。 当两个QObject(或子类)的对象建立了父子关系的时候。子对象就会加入到父对象的一个成员变量叫children(孩子)的list(列表)…...

ubuntu快速安装miniconda
ubuntu快速安装miniconda 环境 ubuntu.22.04 显卡 RTX 3050 关于选择Miniconda还是Anaconda的问题,Anaconda安装包比较大,耗时比较长,如果你是绝对的初学者,选择Anaconda会比较稳妥一些;否则建议你还是选择Miniconda安…...

阿里云游戏服务器多少钱一年?
阿里云游戏服务器租用价格表:4核16G服务器26元1个月、146元半年,游戏专业服务器8核32G配置90元一个月、271元3个月,阿里云服务器网aliyunfuwuqi.com分享阿里云游戏专用服务器详细配置和精准报价: 阿里云游戏服务器租用价格表 阿…...
小游戏和GUI编程(7) | SimpleNN 界面源码解析
小游戏和GUI编程(7) | SimpleNN 界面源码解析 0. 简介 SimpleNN 是 AdamYuan 在高中一年级时用 1 天时间写出来的简易 CNN, 使用 SFML 做 UI, 用于交互式输入手写数字,这个数字被训练好的 CNN 网络执行推理得到识别结果, 它的运行效果如下: 这一篇我们…...
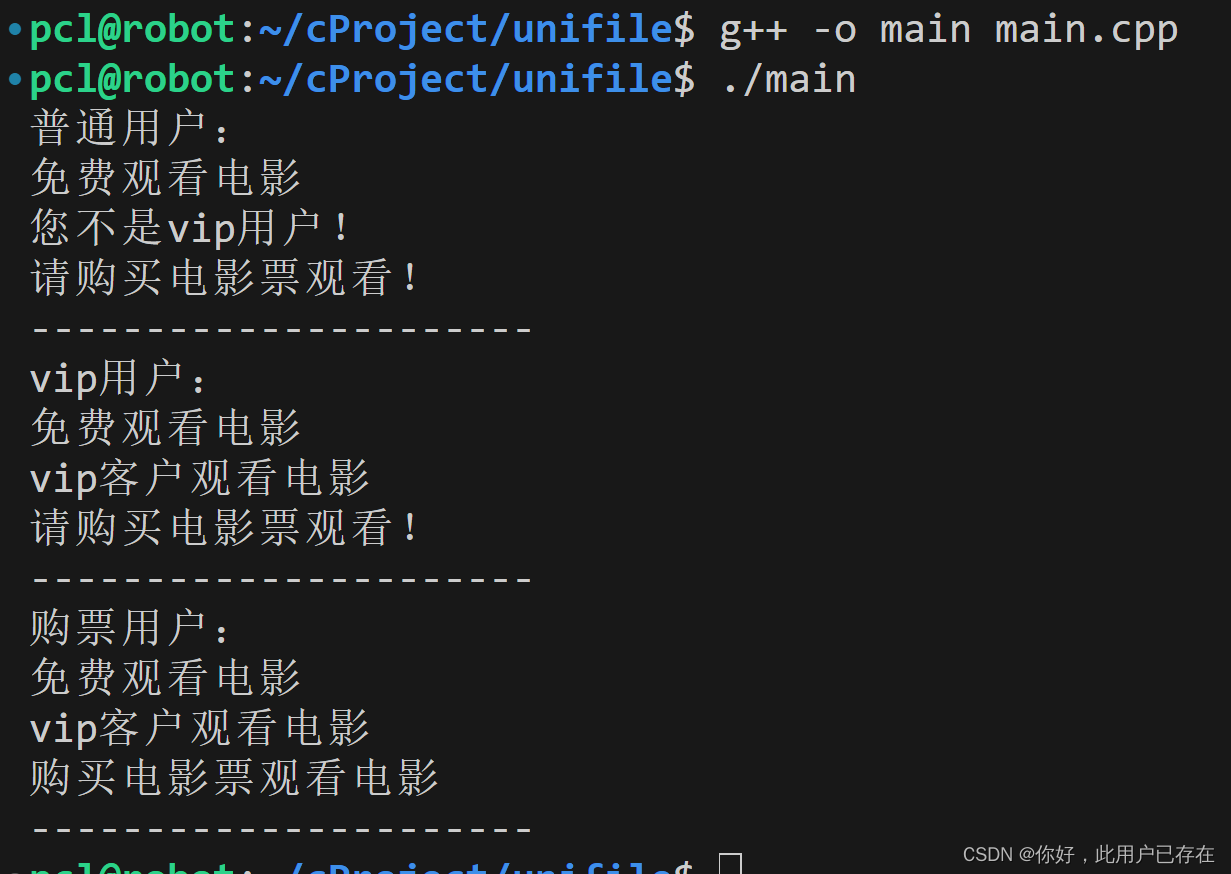
c++设计模式之代理模式
作用 代理模式主要用于,通过代理类,来控制实际对象的访问权限 案例 class VideoSite { public:virtual void freeVideo()0;virtual void vipVideo()0;virtual void trickVideo()0; };class FixBugVideoSite:public VideoSite { public:void freeVideo()…...
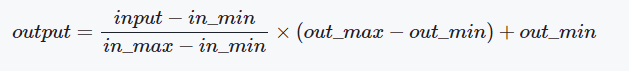
第5个-模糊加载
Day 5 - Blurry Loading 1. 项目展示 2. 分析思路 变化过程 数字从 0 不断增长到 100;中间的百分比数字逐渐消失,即透明度 opacity 从 1 到 0;背景图片从模糊变为清晰,滤镜 filter.blur()的参数设置为从 30px 到 0px。 小 tips…...

rtt设备io框架面向对象学习-adc设备
目录 1.adc设备基类2.adc设备基类的子类3.初始化/构造流程3.1设备驱动层3.2 设备驱动框架层3.3 设备io管理层 4.总结5.使用 1.adc设备基类 此层处于设备驱动框架层。也是抽象类。 在/ components / drivers / include / drivers 下的adc.h定义了如下adc设备基类 struct rt_ad…...

面试官:介绍一下Exception和Error之间的区别
前言 大家好,我是chowley,在我之前的面试中,遇到过这样一个问题:Exception和Error之间有什么区别?今天我就来好好地总结一下! 主体 在Java编程中,Exception和Error都是Java中的可抛出对象&am…...
【RabbitMQ(一)】:基本介绍 | 配置安装与快速入门
应该是新年前最后一篇博客了,明天浅浅休息一下,提前祝大家新年快乐捏!😊😊😊 01. 基础理解 1.1 同步调用和异步调用 👉 同步调用 的时候调用者会 阻塞 等待被调用函数或方法执行完成ÿ…...

ElasticSearch之search API
写在前面 本文看下查询相关内容,这也是我们在实际工作中接触的最多的,所以有必要好好学习下! 1:查询的分类 主要分为如下2类: 1:基于get查询参数的URI search 2:基于post body的request body search&am…...
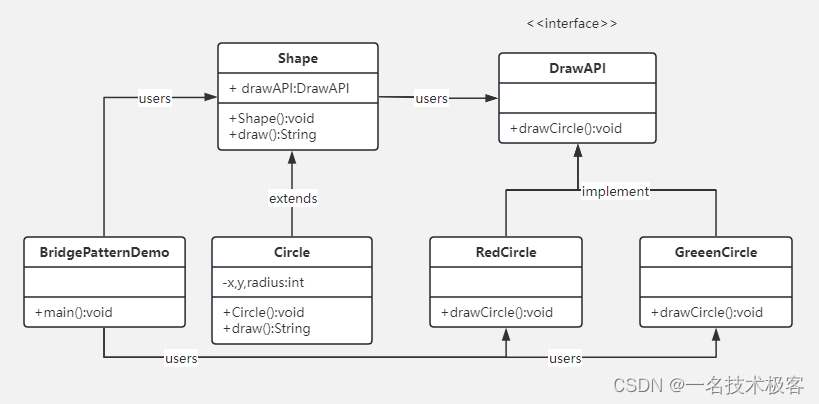
07-Java桥接模式 ( Bridge Pattern )
Java桥接模式 摘要实现范例 桥接模式(Bridge Pattern)是用于把抽象化与实现化解耦,使得二者可以独立变化 桥接模式涉及到一个作为桥接的接口,使得实体类的功能独立于接口实现类,这两种类型的类可被结构化改变而互不影…...
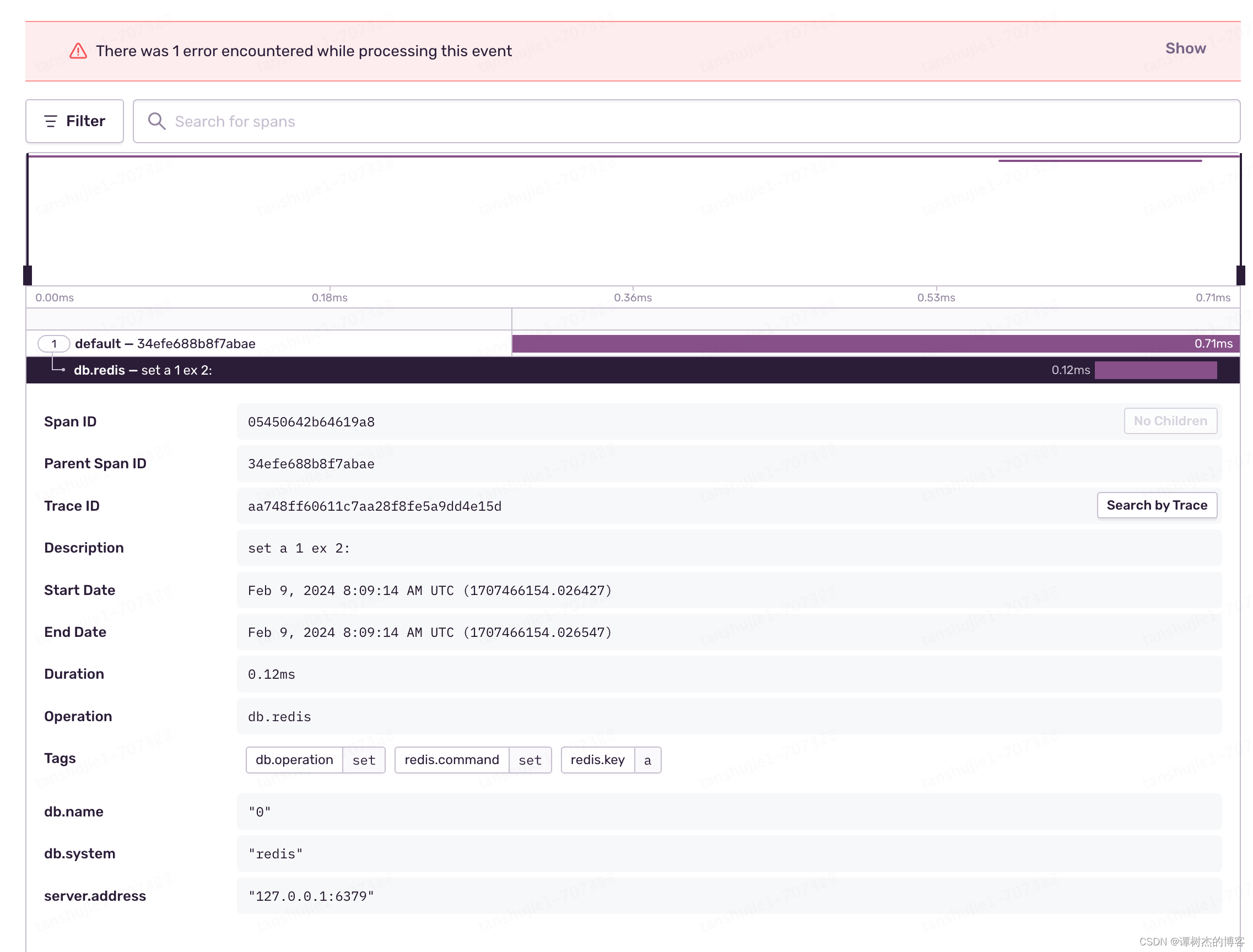
golang集成sentry: go-redis
网上没有找到go-redis集成sentry的库, 所以我简单实现了一个 代码: https://github.com/Shujie-Tan/go-redis-sentry 使用方法: import (redis_sentry "github.com/Shujie-Tan/go-redis-sentry" ) rdb : redis.NewClient(&re…...
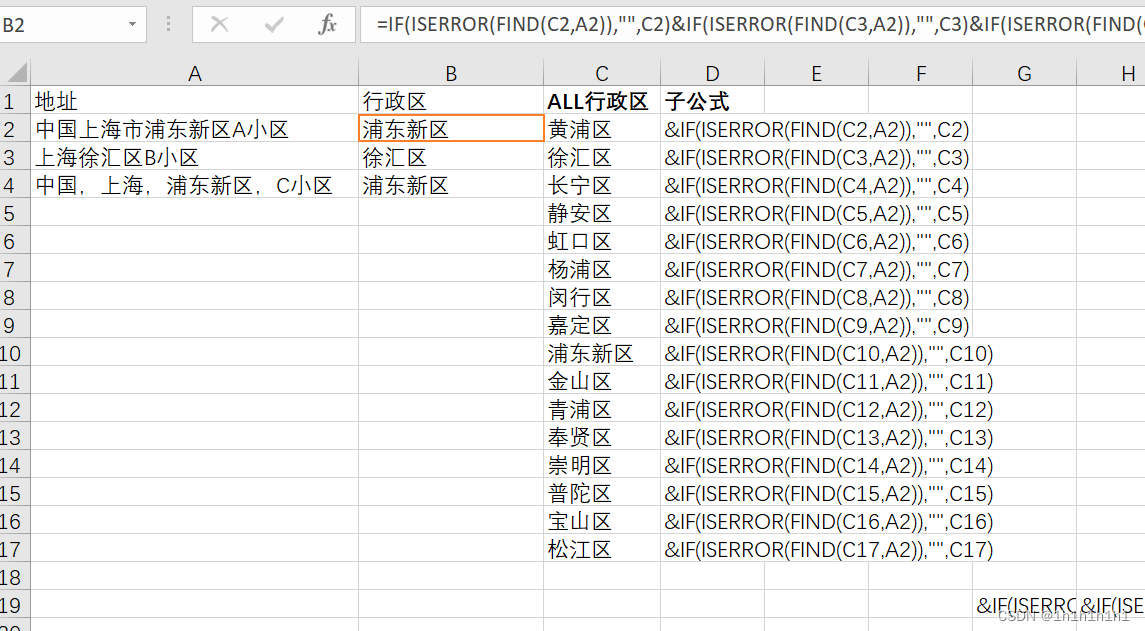
用EXCEL从地址(上海)中提取各区(浦东新区等区)信息
背景: 朋友工作需要经常用EXCEL把各上海用户收货地址中的区提取出来,之前一直手动处理,希望我帮忙用EXCEL公式直接提取处理。 数据样式: 中国上海市浦东新区A小区 上海徐汇区B小区 中国,上海,浦东新区&a…...
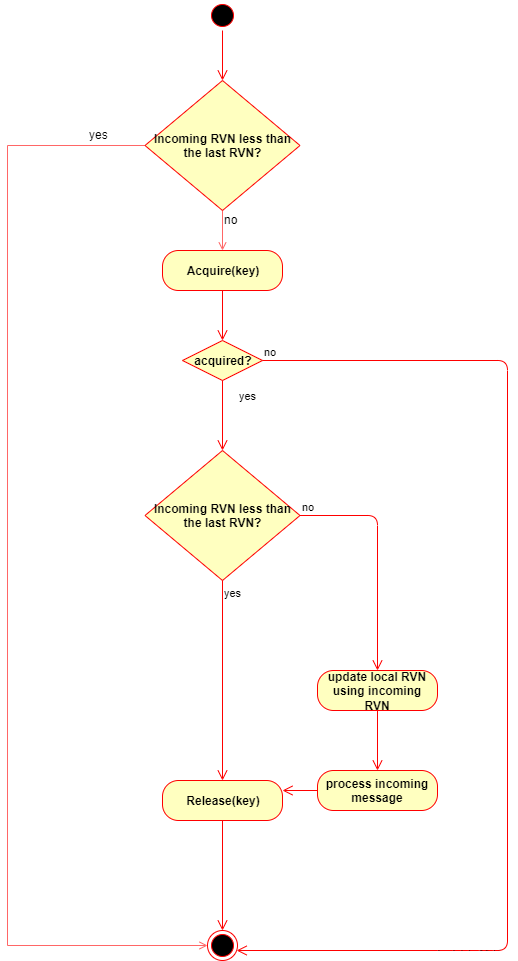
关于在分布式环境中RVN和使用场景的介绍3
简介 在《关于在分布式环境中RVN和使用场景的介绍2》和《关于在分布式环境中RVN和使用场景的介绍1》中我们介绍了RVN的概念和在一些具体用例中的使用。在本文中我们讨论一下在分布式环境中使用RVN需要注意的问题。 问题 我们在收到一条待处理的事件时,需要检查该…...

计算最小公倍数math.lcm()
【小白从小学Python、C、Java】 【计算机等考500强证书考研】 【Python-数据分析】 计算最小公倍数 math.lcm() 请问以下代码输出的结果是? import math print("【执行】math.lcm(2, 4)") print(math.lcm(2, 4)) print("【执行】math.lcm(1, 2, 3…...

VUE SEO 几种方案经典面试题
1、SSR服务器渲染 Vue.js 是构建客户端应用程序的框架。默认情况下,可以再浏览器中输出Vue组件,进行生成DOM和操作DOM。然而,也可以将同一个组件渲染未服务器端的HTML字符串,将它们直接发送到浏览器,最后将这些静态标…...

练习(含atoi的模拟实现,自定义类型等练习)
一、结构体大小的计算及位段 (结构体大小计算及位段 详解请看:自定义类型:结构体进阶-CSDN博客) 1.在32位系统环境,编译选项为4字节对齐,那么sizeof(A)和sizeof(B)是多少? #pragma pack(4)st…...

Qt Widget类解析与代码注释
#include "widget.h" #include "ui_widget.h"Widget::Widget(QWidget *parent): QWidget(parent), ui(new Ui::Widget) {ui->setupUi(this); }Widget::~Widget() {delete ui; }//解释这串代码,写上注释 当然可以!这段代码是 Qt …...

家政维修平台实战20:权限设计
目录 1 获取工人信息2 搭建工人入口3 权限判断总结 目前我们已经搭建好了基础的用户体系,主要是分成几个表,用户表我们是记录用户的基础信息,包括手机、昵称、头像。而工人和员工各有各的表。那么就有一个问题,不同的角色…...

Qt Http Server模块功能及架构
Qt Http Server 是 Qt 6.0 中引入的一个新模块,它提供了一个轻量级的 HTTP 服务器实现,主要用于构建基于 HTTP 的应用程序和服务。 功能介绍: 主要功能 HTTP服务器功能: 支持 HTTP/1.1 协议 简单的请求/响应处理模型 支持 GET…...

04-初识css
一、css样式引入 1.1.内部样式 <div style"width: 100px;"></div>1.2.外部样式 1.2.1.外部样式1 <style>.aa {width: 100px;} </style> <div class"aa"></div>1.2.2.外部样式2 <!-- rel内表面引入的是style样…...

智能分布式爬虫的数据处理流水线优化:基于深度强化学习的数据质量控制
在数字化浪潮席卷全球的今天,数据已成为企业和研究机构的核心资产。智能分布式爬虫作为高效的数据采集工具,在大规模数据获取中发挥着关键作用。然而,传统的数据处理流水线在面对复杂多变的网络环境和海量异构数据时,常出现数据质…...

基于TurtleBot3在Gazebo地图实现机器人远程控制
1. TurtleBot3环境配置 # 下载TurtleBot3核心包 mkdir -p ~/catkin_ws/src cd ~/catkin_ws/src git clone -b noetic-devel https://github.com/ROBOTIS-GIT/turtlebot3.git git clone -b noetic https://github.com/ROBOTIS-GIT/turtlebot3_msgs.git git clone -b noetic-dev…...

浪潮交换机配置track检测实现高速公路收费网络主备切换NQA
浪潮交换机track配置 项目背景高速网络拓扑网络情况分析通信线路收费网络路由 收费汇聚交换机相应配置收费汇聚track配置 项目背景 在实施省内一条高速公路时遇到的需求,本次涉及的主要是收费汇聚交换机的配置,浪潮网络设备在高速项目很少,通…...

Redis:现代应用开发的高效内存数据存储利器
一、Redis的起源与发展 Redis最初由意大利程序员Salvatore Sanfilippo在2009年开发,其初衷是为了满足他自己的一个项目需求,即需要一个高性能的键值存储系统来解决传统数据库在高并发场景下的性能瓶颈。随着项目的开源,Redis凭借其简单易用、…...

pikachu靶场通关笔记19 SQL注入02-字符型注入(GET)
目录 一、SQL注入 二、字符型SQL注入 三、字符型注入与数字型注入 四、源码分析 五、渗透实战 1、渗透准备 2、SQL注入探测 (1)输入单引号 (2)万能注入语句 3、获取回显列orderby 4、获取数据库名database 5、获取表名…...
