蓝桥杯每日一题----唯一分解定理
唯一分解定理
1.内容
任何一个大于1的整数n都可以分解成若干个质数的连乘积,如果不计各个质数的顺序,那么这种分解是惟一的,即若n>1,则有
n = ∏ p i j n=\prod{p^j_i} n=∏pij
这里的 p i p_i pi是质数。可以进行简单证明,假设 p i p_i pi是合数,那么它可以接着分解为两个数相乘的形式,所以最后 p i p_i pi一定是质数。
2.唯一分解定理模板代码
模板代码其实也是唯一分解定理的直接应用,给一个整数n,问有多少个质数是n的约数。这里就需要进行分解,也就是用到了唯一分解定理,我们直接上代码,然后逐一解释难懂的地方。
import java.util.Scanner;public class Main {
public static void main(String[] args) {Scanner scanner = new Scanner(System.in);long n = scanner.nextLong();int ans = 0;for (int i = 2; i <= Math.sqrt(n); i++) {if(n%i==0) ans++;while(n%i == 0) {n = n / i;}}if(n > 1) {ans++;}System.out.println(ans);
}
}
-
一般n可能给的很大,注意最好用long类型
-
我们如果要求一个数的因数,会从1开始遍历进行试除,那么应该遍历到哪里呢?是n吗?其实遍历到 n \sqrt{n} n就可以了。因为如果找到了一个因子为a,那么大于 n \sqrt{n} n的另一个因子就是n/a
-
很明显这个for循环我们是在采用试除法来求n的因子,但是我们如何保证求到的因子是质因子呢?这就是里面的while循环的作用了。给大家举个例子,n=36,6是它的因子,但是不是质因子,那么我们会不会遍历到它呢?i=2时,在while循环里就把36里的所有2都除没了,此时n=9。i=3时,在while循环里就把36里的所有3都除没了,此时n=1。那么此时的n里面已经不包含6了,因为6是由2和3构成的,在遍历到6之前,n里的所有的2和3都没有了,自然也就没有6了。这就是while循环的作用,他保证了我们找到的因子一定是质数。
抽象一点证明,假设q是合数且是n的因子,因为q是合数所有可以被表示成 q = p 1 ∗ p 2 q=p_1*p_2 q=p1∗p2,而 p 1 p_1 p1和 p 2 p_2 p2一定比q小,那么他们一定会在while里面被除去,因此遍历到q时不再包含它们,自然也不会有q。
-
最后一个地方,为什么在代码的最后要加一个if判断呢?还是给大家举一个例子,比如n=396,i=2时,n=99。n=3时,n=11。当i=4时i> n \sqrt{n} n,所以for循环退出了。但是你也可以发现,11也是n的一个质因子,所以我们在最后要判断一下,防止把这种情况漏了。
练习题目
3.应用
(1)求正整数n的正因子个数
假设n的分解公式如下,
n = p 0 j 0 ∗ p 1 j 1 ∗ p 2 j 2 . . . ∗ p k j k n=p^{j_0}_0*p^{j_1}_1*p^{j_2}_2...*p^{j_k}_k n=p0j0∗p1j1∗p2j2...∗pkjk
则n的因子个数为 ( j 0 + 1 ) ∗ ( j 1 + 1 ) ∗ ( j 2 + 1 ) . . . ∗ ( j k + 1 ) (j_0+1)*(j_1+1)*(j_2+1)...*(j_k+1) (j0+1)∗(j1+1)∗(j2+1)...∗(jk+1)个。
简单理解一下,对于 2 3 ∗ 3 2 ∗ 5 3 2^{3}*3^{2}*5^{3} 23∗32∗53来说,可以选择一个2,其余质因子不选,则2是其因子,也可以选择两个2和一个3,则12是其因子,总的来说,假设n包含m个质因子p,则对于p我有m+1中选择,即[0,m]。
做个类比,我有红球3个,绿球5个,他们共有多少种不同的组合,肯定是46吧,那么n的因子个数为 ( j 0 + 1 ) ∗ ( j 1 + 1 ) ∗ ( j 2 + 1 ) . . . ∗ ( j k + 1 ) (j_0+1)*(j_1+1)*(j_2+1)...*(j_k+1) (j0+1)∗(j1+1)∗(j2+1)...∗(jk+1)同理。
模板代码如下,
import java.util.Scanner;public class 约数个数 {
public static void main(String[] args) {Scanner scanner = new Scanner(System.in);long n = 1200000;int ans = 1;for (int i = 2; i <= Math.sqrt(n); i++) {int cnt = 0;while(n%i == 0) {n = n / i;cnt++;}ans *=(cnt+1);}if(n > 1) {ans *= 2;}System.out.println(ans);
}
}练习题目
(2)求正整数n的所有正因子之和
假设n的分解公式如下,
n = p 0 j 0 ∗ p 1 j 1 ∗ p 2 j 2 . . . ∗ p k j k n=p^{j_0}_0*p^{j_1}_1*p^{j_2}_2...*p^{j_k}_k n=p0j0∗p1j1∗p2j2...∗pkjk
则n的所有正因子之和为 s u m = ( p 0 0 + p 0 1 + . . . + p 0 j 0 ) ∗ ( p 1 0 + p 1 1 + . . . + p 1 j 1 ) ∗ . . . ∗ ( p k 0 + p k 1 + . . . + p k j k ) sum=(p_0^0+p_0^1+...+p_0^{j_0})*(p_1^0+p_1^1+...+p_1^{j_1})*...*(p_k^0+p_k^1+...+p_k^{j_k}) sum=(p00+p01+...+p0j0)∗(p10+p11+...+p1j1)∗...∗(pk0+pk1+...+pkjk)个。
这里如果正向推导的话不是很简单,其实对于 p 0 0 p_0^0 p00而言,能够和它相乘成为n的因子的数为 p 1 p_1 p1的幂次里选一个幂次, p 2 p_2 p2的幂次里选一个幂次… p k p_k pk的幂次里选一个幂次,当然对于 p i p_i pi的幂次都会被选择,只是不是同时被选择,既然不是同时,就把他们写成加法,式子 p 0 0 ∗ ( p 1 0 + p 1 1 + . . . + p 1 j 1 ) p_0^0*(p_1^0+p_1^1+...+p_1^{j_1}) p00∗(p10+p11+...+p1j1)表示的是从 p 1 p_1 p1的所有幂次里进行选择与 p 0 0 p_0^0 p00组成一个因子,扩展到其它质数就是 p 0 0 ∗ ( p 1 0 + p 1 1 + . . . + p 1 j 1 ) ∗ . . . ∗ ( p k 0 + p k 1 + . . . + p k j k ) p_0^0*(p_1^0+p_1^1+...+p_1^{j_1})*...*(p_k^0+p_k^1+...+p_k^{j_k}) p00∗(p10+p11+...+p1j1)∗...∗(pk0+pk1+...+pkjk),然后再找对于 p 0 1 p_0^1 p01能够和它相乘成为n的因子的数,可以表示为 p 0 1 ∗ ( p 1 0 + p 1 1 + . . . + p 1 j 1 ) ∗ . . . ∗ ( p k 0 + p k 1 + . . . + p k j k ) p_0^1*(p_1^0+p_1^1+...+p_1^{j_1})*...*(p_k^0+p_k^1+...+p_k^{j_k}) p01∗(p10+p11+...+p1j1)∗...∗(pk0+pk1+...+pkjk),把 p 0 p_0 p0的所有幂次都考虑到就是 ( p 0 0 + p 0 1 + . . . + p 0 j 0 ) ∗ ( p 1 0 + p 1 1 + . . . + p 1 j 1 ) ∗ . . . ∗ ( p k 0 + p k 1 + . . . + p k j k ) (p_0^0+p_0^1+...+p_0^{j_0})*(p_1^0+p_1^1+...+p_1^{j_1})*...*(p_k^0+p_k^1+...+p_k^{j_k}) (p00+p01+...+p0j0)∗(p10+p11+...+p1j1)∗...∗(pk0+pk1+...+pkjk)
4.进阶题目
阶乘约数
问题描述
定义阶乘 n! = 1 × 2 × 3 × ··· × n。
请问 100! (100 的阶乘)有多少个约数。
答案提交
这是一道结果填空的题,你只需要算出结果后提交即可。
本题的结果为一个整数,在提交答案时只填写这个整数,填写多余的内容将无法得分。
题目分析
这是蓝桥杯国赛的一道原题。求一个数的约数个数可以用唯一分解定理在 O ( n ) O(\sqrt{n}) O(n)的时间复杂度内求解。但是100的阶乘确实有点大了,你要是把100的阶乘求出来再去求会超时,并且这个数的存储也是一个问题,当然用java的大整数是可以存的。
这里只能舍弃掉求100的阶乘再求它的约数个数的思路,那应该怎么求呢?回顾一下利用唯一分解定理求解约数个数的过程,先对数字n进行质因数分解,得到式子 n = p 0 j 0 ∗ p 1 j 1 ∗ p 2 j 2 . . . ∗ p k j k n=p^{j_0}_0*p^{j_1}_1*p^{j_2}_2...*p^{j_k}_k n=p0j0∗p1j1∗p2j2...∗pkjk,然后可以求得n的因子个数为 ( j 0 + 1 ) ∗ ( j 1 + 1 ) ∗ ( j 2 + 1 ) . . . ∗ ( j k + 1 ) (j_0+1)*(j_1+1)*(j_2+1)...*(j_k+1) (j0+1)∗(j1+1)∗(j2+1)...∗(jk+1)。其实我们只需要知道数字n里面包含几个 p i p_i pi即可。对于 100 ! = 1 ∗ 2 ∗ 3 ∗ 4... ∗ 100 100!=1*2*3*4...*100 100!=1∗2∗3∗4...∗100,我们可以计算出2里面包含数字2的个数为 a 1 a_1 a1,3里面包含数字2的个数为 a 2 a_2 a2,4里面包含数字2的个数为 a 3 a_3 a3,5里面包含数字2的个数为 a 4 a_4 a4,以此类推直到求到100,那么100!里面包含数字2的个数就是 a 1 + a 2 + a 3 . . . a 99 a_1+a_2+a_3...a_{99} a1+a2+a3...a99。综上我们可以依次对1到100里面的每一个数进行质因数分解,得到的值累加就可以了,最终就可以求出来100进行质因子分解的结果。然后再按照求因子个数的方法进行求解就可以了。
题目代码
public class Main {
public static void main(String[] args) {int p[] = new int[105];for(int i = 2;i <= 100;i++) {int n = i;for(int j = 2;j * j <= n;j++) {while(n%j==0) {p[j]++;n/=j;}}if(n > 0) p[n]++;}long ans = 1;for(int i = 2;i <= 100;i++) {ans *= (p[i]+1);}System.out.println(ans);
}
}
序列求和
问题描述
学习了约数后,小明对于约数很好奇,他发现,给定一个正整数 t,总是可
以找到含有 t 个约数的整数。小明对于含有 t 个约数的最小数非常感兴趣,并
把它定义为 S t S_t St 。
例如 S 1 S_1 S1 = 1, S 2 S_2 S2 = 2, S 3 S_3 S3 = 4, S 4 S_4 S4 = 6,···。
现在小明想知道,前 60 个 S i S_i Si 的和是多少?即 S 1 + S 2 + ⋅ ⋅ ⋅ + S 60 S_1 + S_2 + ··· + S_{60} S1+S2+⋅⋅⋅+S60 是多少?
答案提交
这是一道结果填空的题,你只需要算出结果后提交即可。本题的结果为一
个整数,在提交答案时只填写这个整数,填写多余的内容将无法得分。
题目分析1
这也是蓝桥杯国赛的一道真题。参考题解
考虑一下i=12时怎么求解 S i S_i Si,
12 = 6 ∗ 2 12=6*2 12=6∗2 S i = 2 5 ∗ 3 1 S_i=2^5*3^1 Si=25∗31
12 = 3 ∗ 2 ∗ 2 12=3*2*2 12=3∗2∗2 S i = 2 3 ∗ 3 1 ∗ 5 1 S_i=2^3*3^1*5^1 Si=23∗31∗51
12 = 4 ∗ 3 12=4*3 12=4∗3 S i = 2 3 ∗ 3 2 S_i=2^3*3^2 Si=23∗32
12 = 2 ∗ 2 ∗ 3 12=2*2*3 12=2∗2∗3 S i = 2 1 ∗ 3 1 ∗ 5 2 S_i=2^1*3^1*5^2 Si=21∗31∗52
假设数字n的因数个数有12个,那么根据12的分解结果,可以推出来 S i S_i Si的值(每个乘数间1就是要求的数分解后的质数的幂次),但是这个值并不是唯一的,不同的分解结果有不同的值,同一个分解结果不同的幂次分配方式也对应不同的值。比如 12 = 2 ∗ 2 ∗ 3 12=2*2*3 12=2∗2∗3这种分解结果,如果想要n的值比较小,那么就把这几个数字分配到前3小的质数上,即 S i = 2 1 ∗ 3 1 ∗ 5 2 S_i=2^1*3^1*5^2 Si=21∗31∗52。但是这不是最理想的分配方式。我们将3,2,2降序排序,再减一为2,1,1,那么显然 S i = 2 2 ∗ 3 1 ∗ 5 1 S_i=2^2*3^1*5^1 Si=22∗31∗51要比之前求的 S i = 2 1 ∗ 3 1 ∗ 5 2 S_i=2^1*3^1*5^2 Si=21∗31∗52更小。
总结一下这道题的解题步骤,对于 S i S_i Si,我们dfs搜出i所有的分解情况,然后按照刚刚的办法即对分解降序后求出 S i S_i Si。这样一种分解对应一个值,所有的分解对应的值里面求最小值就是 S i S_i Si。
另外,特判因子数为质数,比如因子数是13,减一是12,这个幂次全部分配给2就是我们要找的最小数。
题目代码1
import java.math.BigInteger;
public class Main {static int n=10000;static int prime[]=new int[n];static int index=0;static BigInteger endBigInteger=new BigInteger("99999999999999999999999999999999999");public static void main(String[] args) {int vis[]=new int[n];for (int i = 2; i <n; i++) {if (vis[i]==0) {prime[index]=i;index++;for (int j = i*i; j <n; j+=i) {vis[j]=1;}}}BigInteger sumBigInteger=new BigInteger("0");for (int i = 1; i <=60; i++) {int vis1[]=new int[i+1];dfs(i,i,0,vis1);sumBigInteger=sumBigInteger.add(endBigInteger);endBigInteger=new BigInteger("99999999999999999999999999999999999");}System.out.println(sumBigInteger);}static void dfs(int Snum,int mid,int start,int vis[]) {if (mid==1) {if (endBigInteger.compareTo(loop(Snum, vis))==1) {endBigInteger=loop(Snum, vis);}return;}for (int i = 2; i <=mid; i++) {if (mid%i==0) {vis[i]++;dfs(Snum,mid/i, start, vis);dfs(Snum,mid/i, start+1, vis);vis[i]--;}}}static BigInteger loop(int num,int vis[]) {int vis2[]=new int[vis.length];for (int i = 0; i < vis.length; i++) {vis2[i]=vis[i];}int index2=0;BigInteger sumBigInteger=new BigInteger("1");for (int i =vis2.length-1; i>0; i--) {if (vis2[i]>0) {sumBigInteger=sumBigInteger.multiply(new BigInteger(prime[index2++]+"").pow(i-1));vis2[i]--;i=i+1;}}return sumBigInteger;}
}
题目分析2
刚刚的分析是比较正规但是也比较麻烦的思路,这道题还有另外一种讨巧的思路。 S i S_i Si最多由4个质数构成,要使值最小那么这4个质数必然是2,3,5,7。我只需要枚举2,3,5,7对应的幂次就可以了。在枚举的过程中记录当前有t个约数的值,和之前记录的值取一个最小。最后求和输出就行。
题目代码2
import java.util.*;
public class Main {static int testCount=60;static int ii=100;static long result[]=new long[61];public static void main(String[] args) {for (int a4 = 0; a4 <= ii; a4++) {for (int a3 = 0; a3 <= ii; a3++) {for (int a2 = 0; a2 <= ii; a2++) {for (int a1 = 0; a1 <= ii; a1++) {int t=(a1+1)*(a2+1)*(a3+1)*(a4+1);if(t<=60) {long single=(long) (Math.pow(2, a1)*Math.pow(3, a2)*Math.pow(5, a3)*Math.pow(7, a4));if(single<result[t] || result[t]==0) {result[t]=single;}}}}}}long sum=0;for (int i = 1; i <= testCount; i++) {sum+=result[i];}System.out.println(sum);}
}
相关文章:

蓝桥杯每日一题----唯一分解定理
唯一分解定理 1.内容 任何一个大于1的整数n都可以分解成若干个质数的连乘积,如果不计各个质数的顺序,那么这种分解是惟一的,即若n>1,则有 n ∏ p i j n\prod{p^j_i} n∏pij 这里的 p i p_i pi是质数。可以进行简单证明…...

openssl3.2 - osslsigncode工程的学习
文章目录 openssl3.2 - osslsigncode工程的学习概述笔记工程库地址工程的编译osslsigncodeM工程文件列表osslsigncodeM工程搭建细节原始工程实现的改动自己封装的包含openssl和curl的实现osslsigncodeM工程命令行的用法备注 - VS2019调试环境备注 - 如果要单步openssl的API学学…...
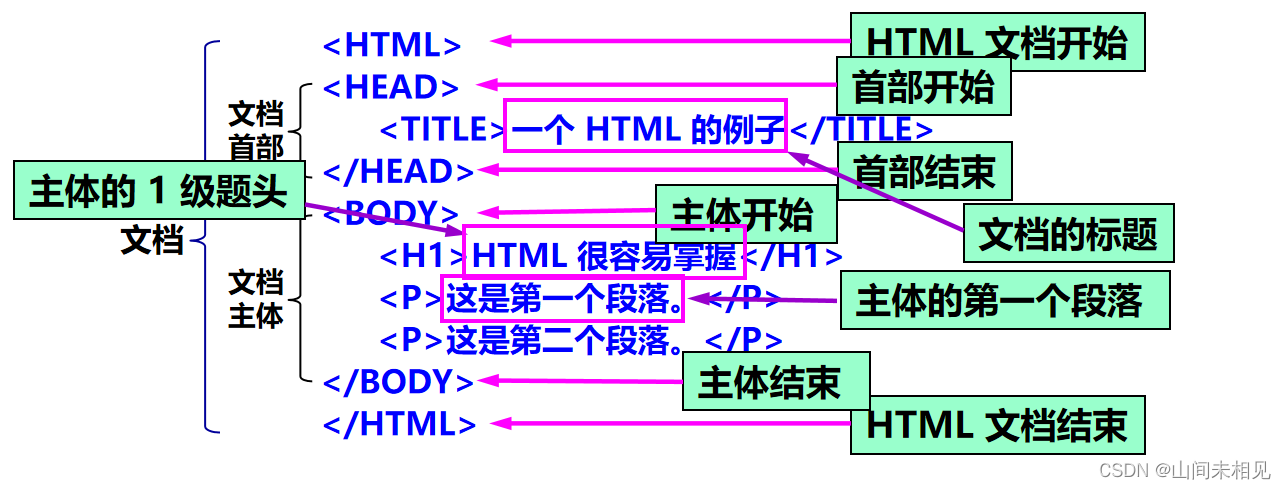
HTML 超文本标记语言
超文本标记语言 HTML 在一个客户程序主窗口上显示出的万维网文档称为页面 (page)。 页面制作的标准语言:HTML。 超文本标记语言 HTML (HyperText Markup Language) 是一种制作万维网页面的标准语言,它消除了不同计算机之间信息交流的障碍,…...

sklearn:机器学习 分类特征编码category_encoders
文章目录 category_encoders简介OrdinalEncoder 序列编码OneHotEncoder 独热编码TargetEncoder 目标编码Binary Encoder 二进制编码BaseNEncoder 贝叶斯编码LeaveOneOutEncoder 留一法HashingEncoder 哈希编码CatBoostEncoder catboost目标编码CountEncoder 频率编码WOEEncoder…...
‘ is ambiguous)
C++错误[错误] call of overloaded ‘min(int, int)‘ is ambiguous
错误代码: #include<iostream> using namespace std;template <class T> T min(T x,T y){if(x<y){return x;}else return y; }int main(){int n12,n210;double d11.5,d25.6;cout<<min(n1,n2)<<endl;cout<<min(d1,d2)<<endl…...

2024全栈元年-thinkphp-数据操作
thinkphp 数据相关操作 1.单数据查询 1、单数据查询 ,Db::table(‘tp_stu’) 必须加前缀 2、如果只是查询符合条件的使用where find,如果没有符合条件的返回null 3、使用 findOrFail 没有数据会抛出异常 4、使用 findOrEmpty 没有数据会返回【】 5、得到最近一个原生SQL …...

HTML世界之第二重天
目录 一、HTML 格式化 1.HTML 文本格式化标签 2.HTML "计算机输出" 标签 3.HTML 引文, 引用, 及标签定义 二、HTML 链接 1.HTML 链接 2.HTML 超链接 3.HTML 链接语法 4.文本链接 5.图像链接 6.锚点链接 7.下载链接 8.Target 属性 9.Id 属性 三、HTML …...

社区经营的好处与优势:为何越来越多的人选择社区店?
社区店,这个曾经被视为小型、局限的商业模式,如今正逐渐崭露头角,成为众多创业者和消费者的首选。 特别是在鲜奶吧这样的细分市场中,社区店更是展现出了其独特的魅力和优势。作为一名拥有五年鲜奶吧经营经验的创业者,…...

C语言系列1——详解C语言:变量、常量与数据类型
目录 写在开始1. 变量与常量的概念1.1. 变量1.2. 常量1.3. 变量与常量的比较1.4. 选择变量还是常量 2. C语言中的基本数据类型2.1. 整型(Integer Types)2.2. 浮点型(Floating-Point Types)2.3. 字符型(Character Type&…...
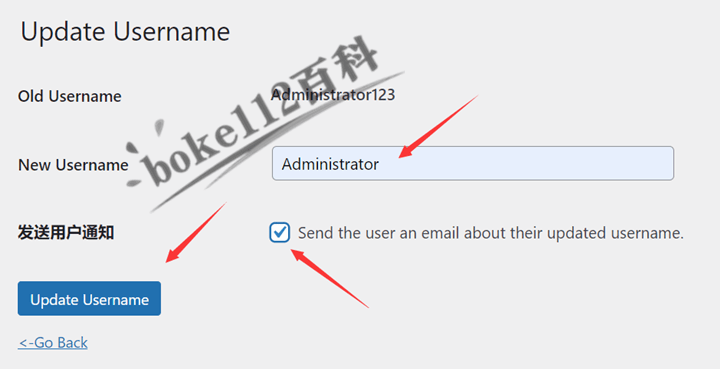
WordPress修改所有用户名并发送邮件通知的插件Easy Username Updater
前面跟大家介绍了『如何修改WordPress后台管理员用户名?推荐2种简单方法』一文,但是对于有很多用户的站长来说,操作有点复杂,而且无法发邮件通知对方,所以今天boke112百科向大家推荐一款可以直接在WordPress后台修改所…...
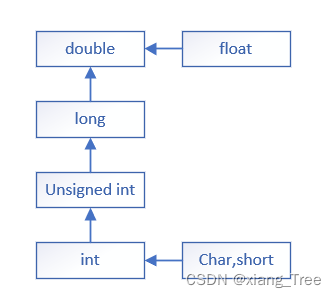
C语言中的数据类型-强转
强制类型转换 概念:将某种类型的数据转化我们需要的数据类型,注意强制类型转化是临时强转,不会改变本身的数据类型。 强转又分为显式强转和隐式转化 显示强转是按照我们的要求进行转化 格式:(需要转化数据类型)变量名 #inclu…...
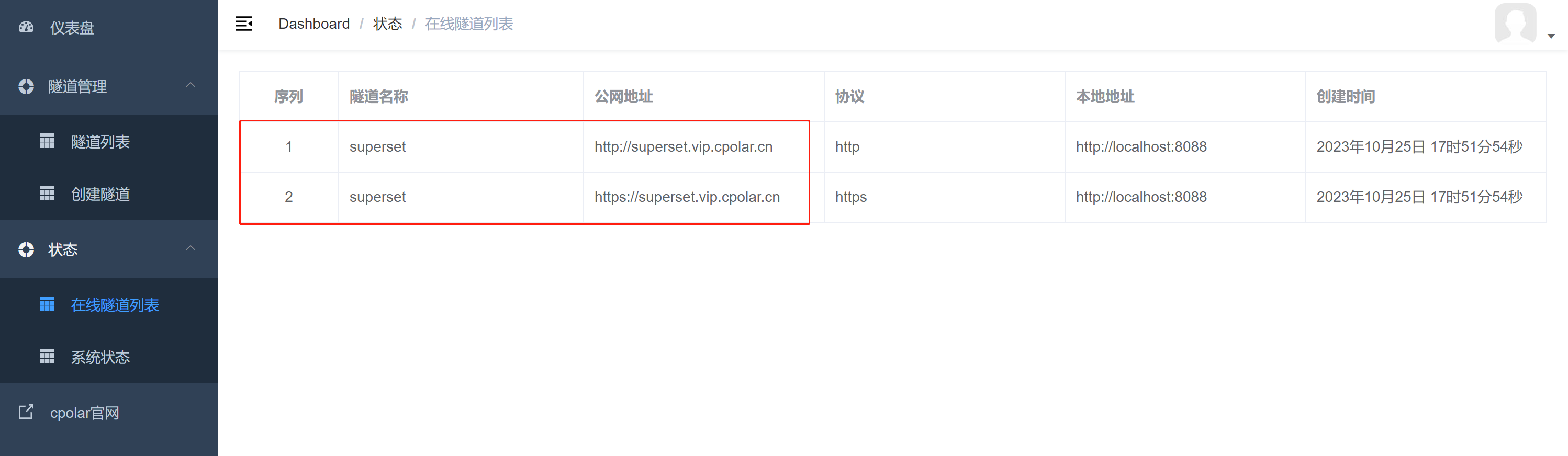
大数据可视化BI分析工具Apache Superset结合内网穿透实现远程访问
文章目录 前言1. 使用Docker部署Apache Superset1.1 第一步安装docker 、docker compose1.2 克隆superset代码到本地并使用docker compose启动 2. 安装cpolar内网穿透,实现公网访问3. 设置固定连接公网地址 前言 Superset是一款由中国知名科技公司开源的“现代化的…...

C# 线程与线程池的使用方法、注意事项
在C#中,线程和线程池是两种用于实现多线程编程的方式。线程用于执行并发任务,而线程池提供了一种更有效率的方式来管理和复用线程资源。 C# 线程(System.Threading.Thread) 创建和启动线程: Thread thread new Thre…...
)
2024年华为OD机试真题-按身高和体重排队-Python-OD统一考试(C卷)
题目描述: :某学校举行运动会,学生们按编号(1、2、3…n)进行标识,现需要按照身高由低到高排列,对身高相同的人,按体重由轻到重排列;对于身高体重都相同的人,维持原有的编号顺序关系。请输出排列后的学生编号。 输入描述:两个序列,每个序列由n个正整数组成(0 < n …...

openGauss学习笔记-218 openGauss性能调优-确定性能调优范围-硬件瓶颈点分析-I/O
文章目录 openGauss学习笔记-218 openGauss性能调优-确定性能调优范围-硬件瓶颈点分析-I/O218.1 查看I/O状况218.2 性能参数分析 openGauss学习笔记-218 openGauss性能调优-确定性能调优范围-硬件瓶颈点分析-I/O 获取openGauss节点的CPU、内存、I/O和网络资源使用情况…...
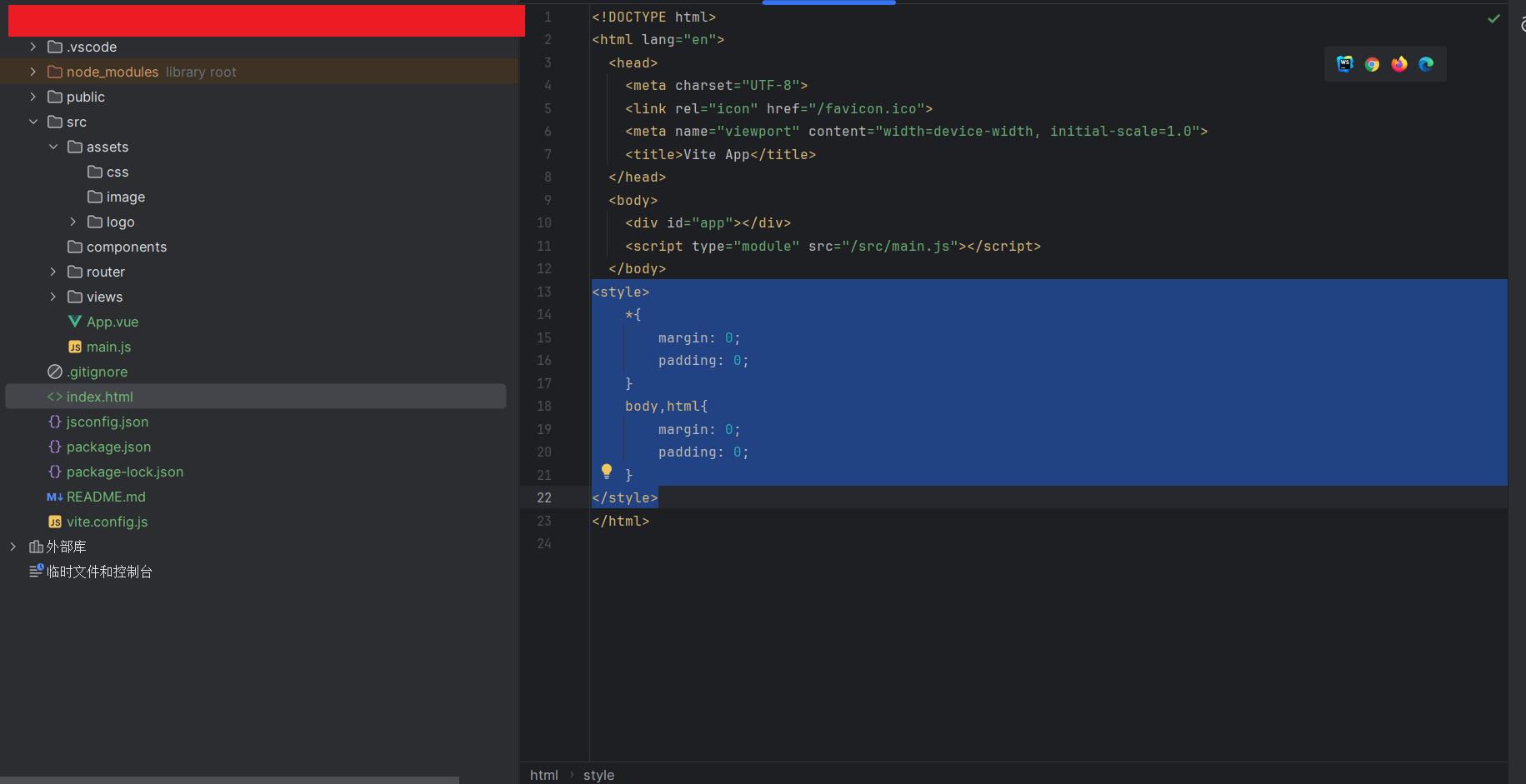
去除vue自带的边距
使用vue时发现总有去不掉的外边距,在index.vue里面怎样设置样式都不管用 查阅资料后发现要在vue项目自带的index.html文件内添加下面的样式代码才行 <style>*{margin: 0;padding: 0;}body,html{margin: 0;padding: 0;} </style>...
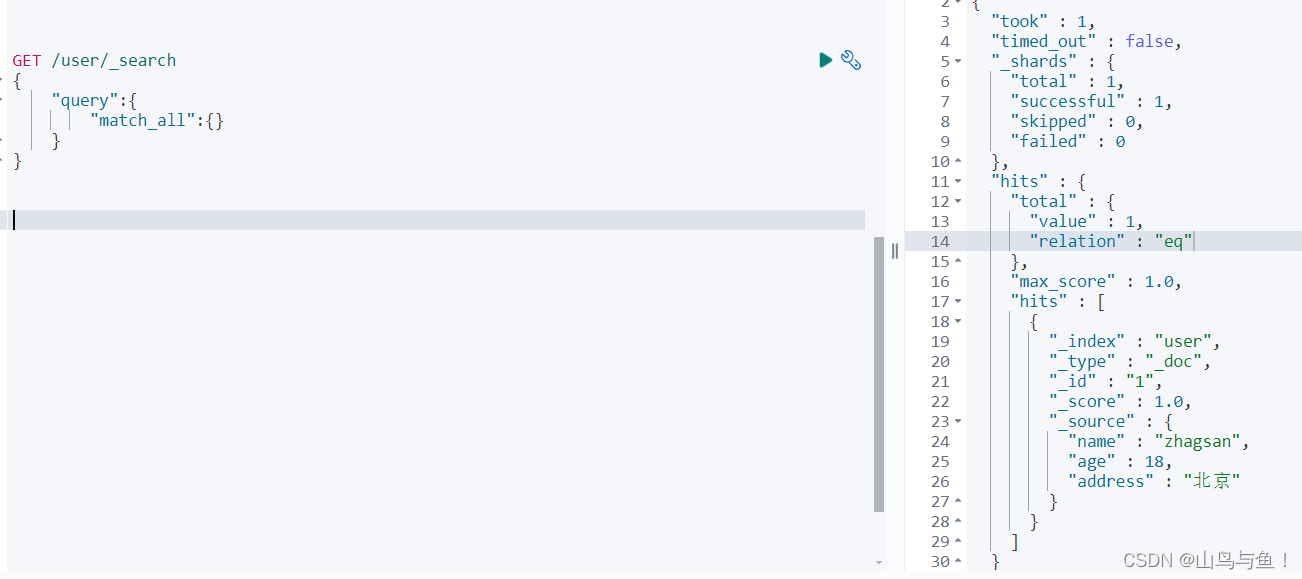
ElasticSearch级查询Query DSL上
目录 ES高级查询Query DSL match_all 返回源数据_source 返回指定条数size 分页查询from&size 指定字段排序sort 术语级别查询 Term query术语查询 Terms Query多术语查询 exists query ids query range query范围查询 prefix query前缀查询 wildcard query通…...

120.乐理基础-五线谱-五线谱的多声部与指法问题
内容参考于:三分钟音乐社 上一个内容:119.乐理基础-五线谱-五线谱的标记-CSDN博客 五线谱多声部与简谱的多声部一样:简谱的多声部 五线谱多声部例子:钢琴谱 另一个例子:在纵向上有多个音符 然后放大之后,…...

YOLOv5独家改进:上采样算子 | 超轻量高效动态上采样DySample,效果秒杀CAFFE,助力小目标检测
💡💡💡本文独家改进:一种超轻量高效动态上采样DySample, 具有更少的参数、FLOPs,效果秒杀CAFFE和YOLOv5网络中的nn.Upsample 💡💡💡在多个数据集下验证能够涨点,尤其在小目标检测领域涨点显著。 收录 YOLOv5原创自研 https://blog.csdn.net/m0_63774211/cate…...
)
洛谷 P1102 A-B 数对 (Java)
洛谷 P1102 A-B 数对 (Java) 传送门:P1102 A-B 数对 题目: A-B 数对 题目背景 出题是一件痛苦的事情! 相同的题目看多了也会有审美疲劳,于是我舍弃了大家所熟悉的 AB Problem,改用 A-B 了哈哈! 题目描…...

【大模型RAG】拍照搜题技术架构速览:三层管道、两级检索、兜底大模型
摘要 拍照搜题系统采用“三层管道(多模态 OCR → 语义检索 → 答案渲染)、两级检索(倒排 BM25 向量 HNSW)并以大语言模型兜底”的整体框架: 多模态 OCR 层 将题目图片经过超分、去噪、倾斜校正后,分别用…...

超短脉冲激光自聚焦效应
前言与目录 强激光引起自聚焦效应机理 超短脉冲激光在脆性材料内部加工时引起的自聚焦效应,这是一种非线性光学现象,主要涉及光学克尔效应和材料的非线性光学特性。 自聚焦效应可以产生局部的强光场,对材料产生非线性响应,可能…...

在HarmonyOS ArkTS ArkUI-X 5.0及以上版本中,手势开发全攻略:
在 HarmonyOS 应用开发中,手势交互是连接用户与设备的核心纽带。ArkTS 框架提供了丰富的手势处理能力,既支持点击、长按、拖拽等基础单一手势的精细控制,也能通过多种绑定策略解决父子组件的手势竞争问题。本文将结合官方开发文档,…...

线程与协程
1. 线程与协程 1.1. “函数调用级别”的切换、上下文切换 1. 函数调用级别的切换 “函数调用级别的切换”是指:像函数调用/返回一样轻量地完成任务切换。 举例说明: 当你在程序中写一个函数调用: funcA() 然后 funcA 执行完后返回&…...

连锁超市冷库节能解决方案:如何实现超市降本增效
在连锁超市冷库运营中,高能耗、设备损耗快、人工管理低效等问题长期困扰企业。御控冷库节能解决方案通过智能控制化霜、按需化霜、实时监控、故障诊断、自动预警、远程控制开关六大核心技术,实现年省电费15%-60%,且不改动原有装备、安装快捷、…...

【Web 进阶篇】优雅的接口设计:统一响应、全局异常处理与参数校验
系列回顾: 在上一篇中,我们成功地为应用集成了数据库,并使用 Spring Data JPA 实现了基本的 CRUD API。我们的应用现在能“记忆”数据了!但是,如果你仔细审视那些 API,会发现它们还很“粗糙”:有…...

什么是Ansible Jinja2
理解 Ansible Jinja2 模板 Ansible 是一款功能强大的开源自动化工具,可让您无缝地管理和配置系统。Ansible 的一大亮点是它使用 Jinja2 模板,允许您根据变量数据动态生成文件、配置设置和脚本。本文将向您介绍 Ansible 中的 Jinja2 模板,并通…...

项目部署到Linux上时遇到的错误(Redis,MySQL,无法正确连接,地址占用问题)
Redis无法正确连接 在运行jar包时出现了这样的错误 查询得知问题核心在于Redis连接失败,具体原因是客户端发送了密码认证请求,但Redis服务器未设置密码 1.为Redis设置密码(匹配客户端配置) 步骤: 1).修…...

PAN/FPN
import torch import torch.nn as nn import torch.nn.functional as F import mathclass LowResQueryHighResKVAttention(nn.Module):"""方案 1: 低分辨率特征 (Query) 查询高分辨率特征 (Key, Value).输出分辨率与低分辨率输入相同。"""def __…...

Bean 作用域有哪些?如何答出技术深度?
导语: Spring 面试绕不开 Bean 的作用域问题,这是面试官考察候选人对 Spring 框架理解深度的常见方式。本文将围绕“Spring 中的 Bean 作用域”展开,结合典型面试题及实战场景,帮你厘清重点,打破模板式回答,…...
