Python数学建模之回归分析
1.基本概念及应用场景
回归分析是一种预测性的建模技术,数学建模中常用回归分析技术寻找存在相关关系的变量间的数学表达式,并进行统计推断。例如,司机的鲁莽驾驶与交通事故的数量之间的关系就可以用回归分析研究。回归分析根据变量的数目分为一元回归和多元回归,根据自变量和因变量的表现形式分为线性和非线性。
回归模型:描述因变量y如何依赖于自变量x和误差项e的方程。
回归方程:描述因变量y如何依赖于自变量x的方程。
2.回归分析的一般步骤
- 确定回归方程中的解释变量和被解释变量
- 确定回归模型,建立回归方程
- 对回归方程进行各种检验
- 用回归方程进行预测
3.一元线性回归分析
1.概念
例子:
- 人均收入是否显著影响人均食品消费支出
- 贷款余额是否影响到不良贷款
- 航班正点率是否对顾客投诉次数有显著影响
回归模型:
:截距
:斜率
:误差项,反映随机因数对y的影响,是不可避免的
回归方程:
若回归方程中的未知参数已知,则对于给定的x值,可计算出y的期望值。
用样本统计量代替未知参数,就得到估计的回归方程,称回归直线。
2.最小二乘法求参数
常用最小二乘法,即使残差(因变量的观察值与估计值的离差)平方和达到最小求参数:
展开:
求偏导并整理:
代入数据即可得到及
3.点估计
将x的值代入回归方程即可得对应的点估计值。
4.区间估计
估计标准误差:
估计标准误差越小,则数据点围绕回归直线的分散程度越小,回归方程的代表性越大,可靠性越高。
置信区间:
预测区间:
:显著性水平
:置信水平
:即
,n-k为残差自由度(样本容量-回归系数的数量),一元线性回归方程中k=2
模型建立和求解的Python代码:
import numpy as np
import statsmodels.api as sm
import scipy.stats as stats
import matplotlib.pyplot as plt
plt.rc('font', family='SimHei') # 用来正常显示中文标签
plt.rc('axes', unicode_minus=False) # 用来正常显示负号# 输入数据
x = np.array([143, 145, 146, 147, 149, 150, 153, 154, 155, 156, 157, 158, 159, 160, 162, 164])
y = np.array([88, 85, 88, 91, 92, 93, 93, 95, 96, 98, 97, 96, 98, 99, 100, 102])# 添加截距项
X = sm.add_constant(x)# 求参数值
model = sm.OLS(y, X).fit()
beta = model.params
print("参数值:")
print("beta0 =", beta[0])
print("beta1 =", beta[1])# 点估计
x0 = float(input("x="))
y_pred = beta[0] + beta[1] * x0
print("点估计预测值:", y_pred)# 计算标准误差
se = np.sqrt(model.mse_resid)# 自由度
n = len(x)
df = n - model.df_model - 1# 置信水平和 t 分位数
alpha = 0.05
t = np.abs(stats.t.ppf(alpha/2, df))# 计算置信区间和预测区间
x_mean = np.mean(x)
x_var = np.sum((x - x_mean)**2)
conf_interval = t * se * np.sqrt(1/n + (x - x_mean)**2 / x_var)
pred_interval = t * se * np.sqrt(1 + 1/n + (x - x_mean)**2 / x_var)# 绘制原始数据和回归直线
plt.scatter(x, y, color='blue', marker='*', label='原始数据')
plt.plot(x, model.fittedvalues, color='red', label='回归直线')
plt.xlabel('x')
plt.ylabel('y')# 绘制置信区间和预测区间
plt.fill_between(x, model.fittedvalues - conf_interval, model.fittedvalues + conf_interval, color='gray', alpha=0.3, label='置信区间')
plt.fill_between(x, model.fittedvalues - pred_interval, model.fittedvalues + pred_interval, color='yellow', alpha=0.3, label='预测区间')plt.legend()
plt.show()
5.模型检验
1.回归直线的拟合优度
回归直线与各观测点的接近程度称为回归直线对数据的拟合优度。
评价拟合优度的指标:
- 总平方和(TSS):反映因变量的n个观测值与其均值的总离差
- 回归平方和(ESS):反映了y的总变差中,由于x与y之间的线性关系引起的y的变化部分
- 残差平方和(RSS):反映了其他因素对y变差的作用,是不能由回归直线来解释的y的变差部分
99
相关文章:
Python数学建模之回归分析
1.基本概念及应用场景 回归分析是一种预测性的建模技术,数学建模中常用回归分析技术寻找存在相关关系的变量间的数学表达式,并进行统计推断。例如,司机的鲁莽驾驶与交通事故的数量之间的关系就可以用回归分析研究。回归分析根据变量的…...
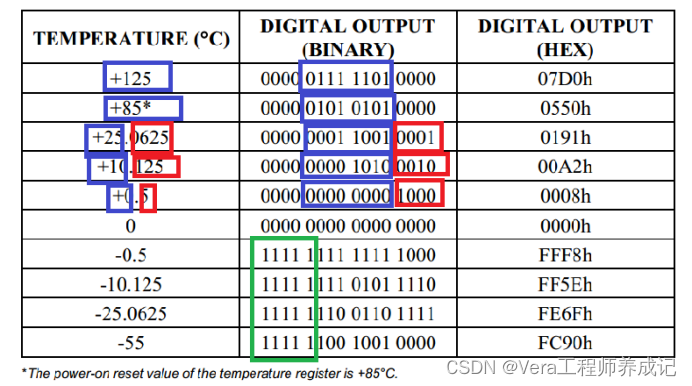
单片机学习笔记---DS18B20温度传感器
目录 DS18B20介绍 模拟温度传感器的基本结构 数字温度传感器的应用 引脚及应用电路 DS18B20的原理图 DS18B20内部结构框图 暂存器内部 单总线介绍 单总线电路规范 单总线时序结构 初始化 发送一位 发送一个字节 接收一位 接收一个字节 DS18B20操作流程 指令介…...
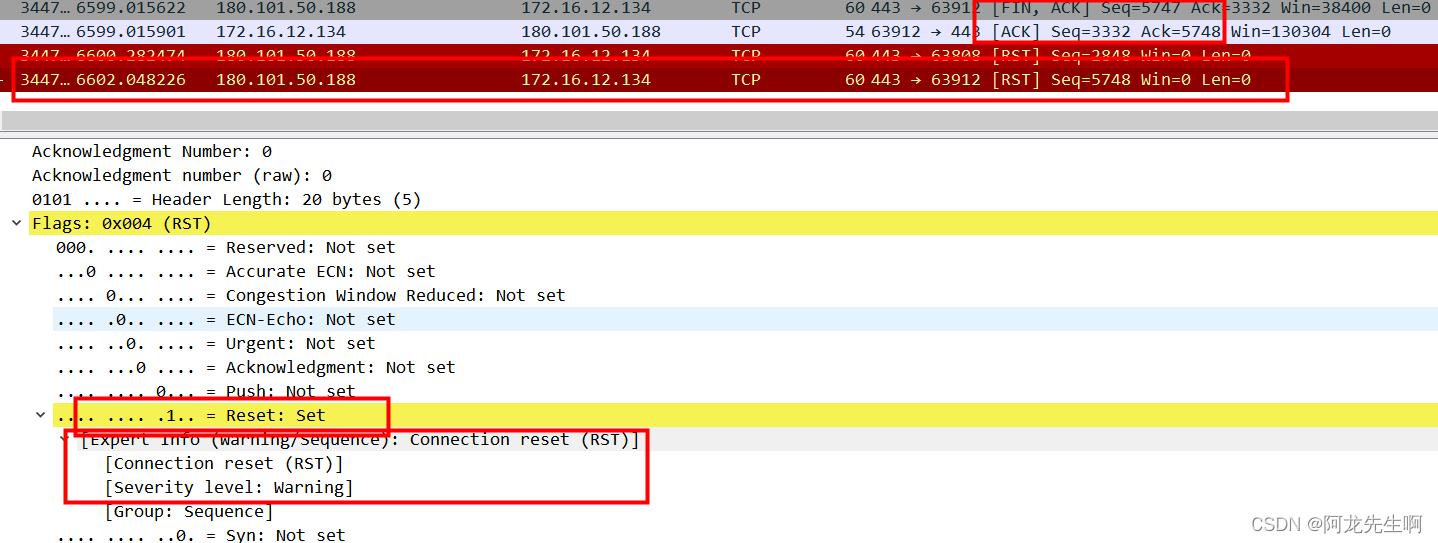
【网络】WireShark过滤 | WireShark实现TCP三次握手和四次挥手
目录 一、开启WireShark的大门 1.1 WireShark简介 1.2 常用的Wireshark过滤方式 二、如何抓包搜索关键字 2.1 协议过滤 2.2 IP过滤 编辑 2.3 过滤端口 2.4 过滤MAC地址 2.5 过滤包长度 2.6 HTTP模式过滤 三、ARP协议分析 四、WireShark之ICMP协议 五、TCP三次握…...
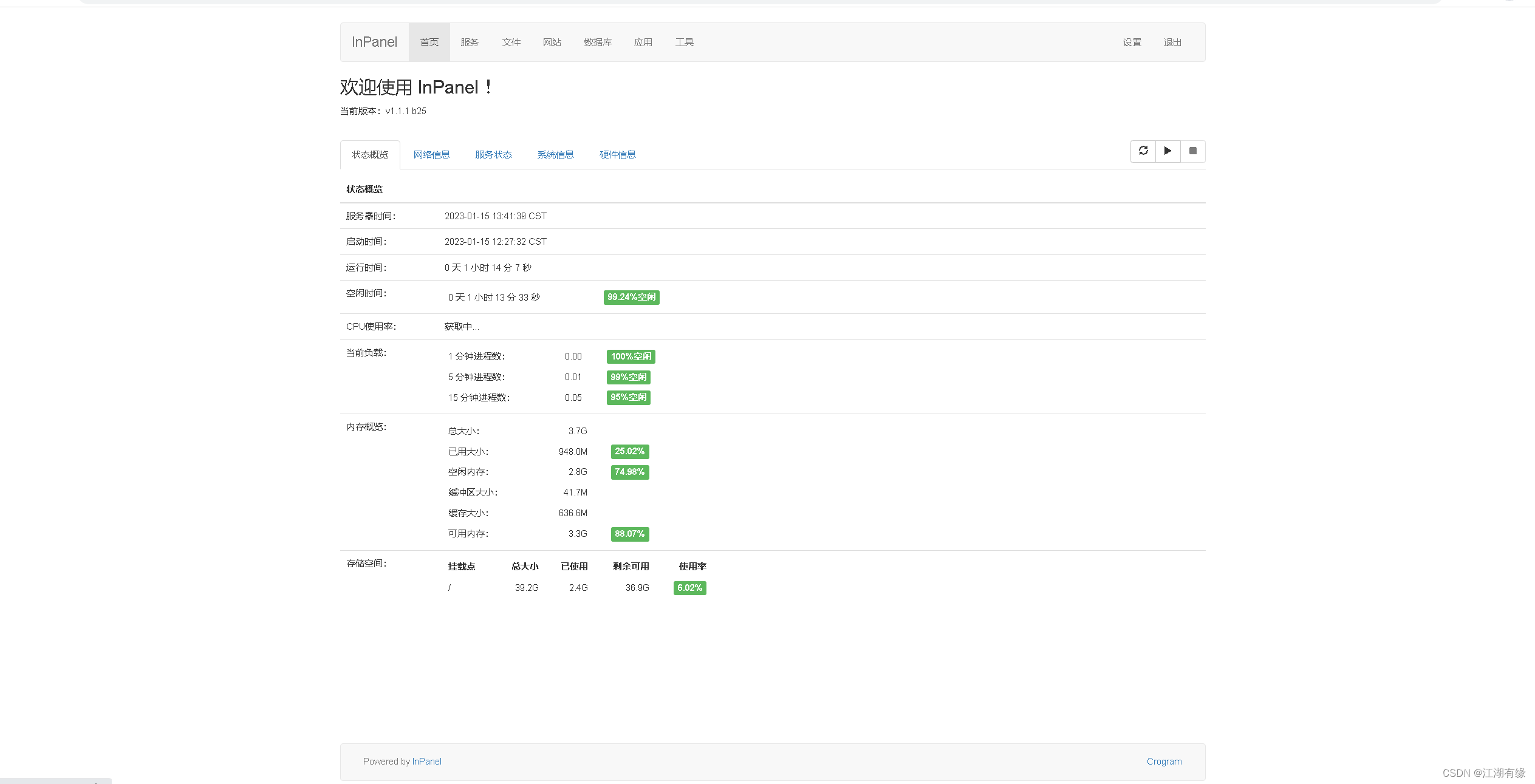
开源免费的Linux服务器管理面板分享
开源免费的Linux服务器管理面板分享 一、1Panel1.1 1Panel 简介1.2 1Panel特点1.3 1Panel面板首页1.4 1Panel使用体验 二、webmin2.1 webmin简介2.2 webmin特点2.3 webmin首页2.4 webmin使用体验 三、Cockpit3.1 Cockpit简介3.2 Cockpit特点3.3 Cockpit首页3.4 Cockpit使用体验…...

leetcode算法-位运算
位运算,直接在二进制上进行的按位操作,位运算的种类如下: 1.按位异或^:异或的含义是操作的两位不同,则结果为1,相同则结果为0,所以两个相同的数异或,结果应该是0,3^3的结果是0,3^4的…...

「MySQL」约束
概述 分类 约束描述关键字非空约束限制该字段的数据不能为 nullNOT NULL唯一约束保证该字段的所有数据都是唯一、不重复的UNIQUE主键约束主键是一行数据的唯一标识,要求非空且唯一PRIMARY KEY默认约束保存数据时,如果未指定该字段的值,则采…...
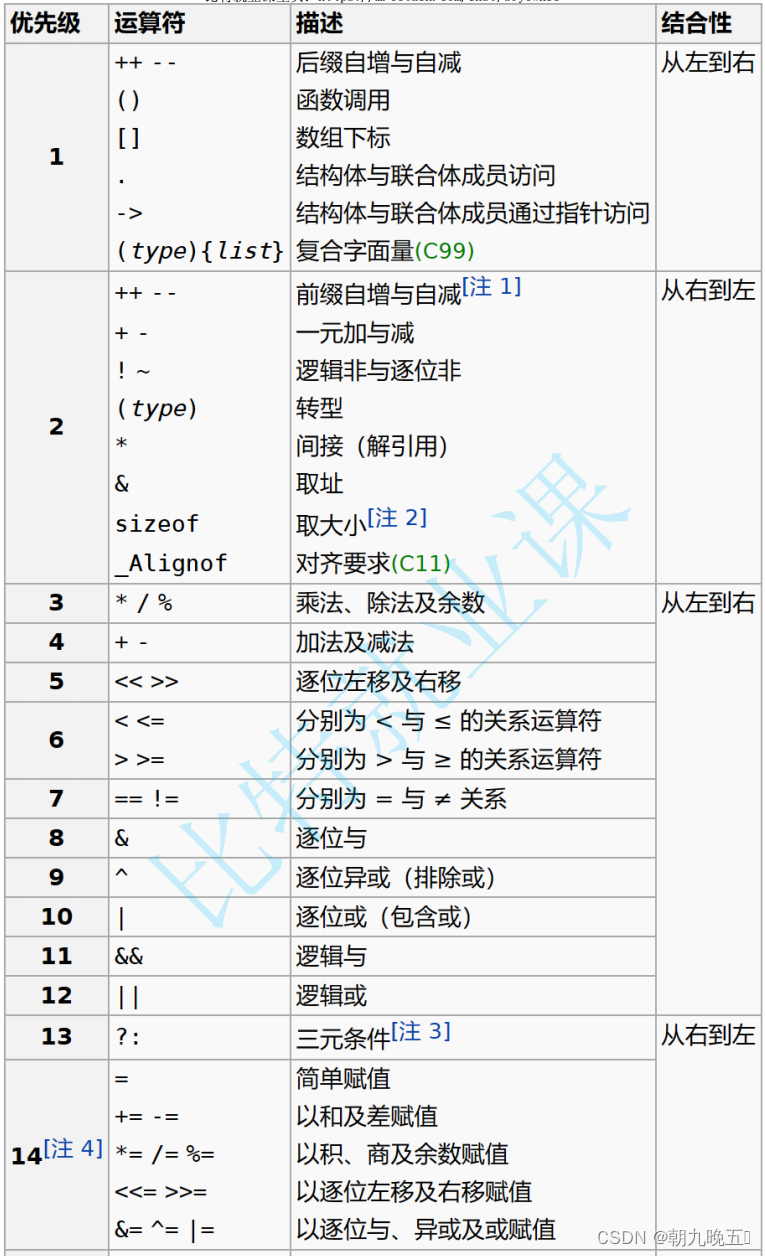
C语言:详解操作符(下)
上一篇链接:C语言:详解操作符(上)摘要: 在上篇文章中,我们已经讲过位操作符等涉及二进制的操作符,这些有助于帮助我们后期理解数据如何在计算机中运算并存储,接下来本篇将更多的讲述…...

Vue3.0(六):VueX 4.x详解
Vuex4状态管理 什么是状态管理 在开发中,我们的应用程序需要处理各种各样的数据,这些数据需要保存在应用程序的某一个位置,对于这些数据的管理,就是 状态管理目前前端项目越来越复杂,多组件共享同一数据的状态很常见…...
))
突破编程_C++_面试(基础知识(13))
面试题45:C中的字符串如何存储 在C中,字符串可以通过多种方式存储,但最常见和推荐使用的方式是通过 std::string 类,该类位于 <string> 头文件中。std::string 是一个类模板的实例,通常用于存储字符数组&#x…...

掌握C语言文件操作:从入门到精通的完整指南!
✨✨ 欢迎大家来到贝蒂大讲堂✨✨ 🎈🎈养成好习惯,先赞后看哦~🎈🎈 所属专栏:C语言学习 贝蒂的主页:Betty‘s blog 1. 什么是文件 文件其实是指一组相关数据的有序集合。这个数据集有一个名称&a…...

JavaEE作业-实验二
目录 1 实验内容 2 实验要求 3 思路 4 核心代码 5 实验结果 1 实验内容 实现两个整数求和的WEB程序 2 实验要求 ①采用SpringMVC框架实现 ②数据传送到WEB界面采用JSON方式 3 思路 ①创建一个SpringMVC项目,配置好相关的依赖和配置文件。 ②创建一个Con…...

2月8号作业
Sqlite3系统命令 .quit 退出数据库 .exit 退出数据库 .help 显示帮助信息,获取所有系统命令 .table 查看当前数据库下的所有表格 .schema 查看表的结构 Sqlite3语句 创建表格: create table 表名 (字段名 数据类型, 字段名 数据类型); create table if…...

08:K8S资源对象管理|服务与负载均衡|Ingress
K8S资源对象管理|服务与负载均衡|Ingress DaemonSet控制器污点策略容忍容忍污点 其他资源对象Job资源对象 有限生命周期CronJob资源对象 集群服务服务自动发现headless服务 实现服务定位与查找 服务类型 Ingress插件 发布服务的方式 DaemonSet控制器 Da…...

HarmonyOS 横屏调试与真机横屏运行
我们有些程序 需要横屏才能执行出效果 我们在预览器上 点击如下图指向出 就进入一个横屏调试了 但 我们真机运行 依旧是竖着的 我们如下图 找到 module.json5 在 abilities 下面 第一个对象 最下面 加上 "orientation": "landscape"然后 我们再真机运…...
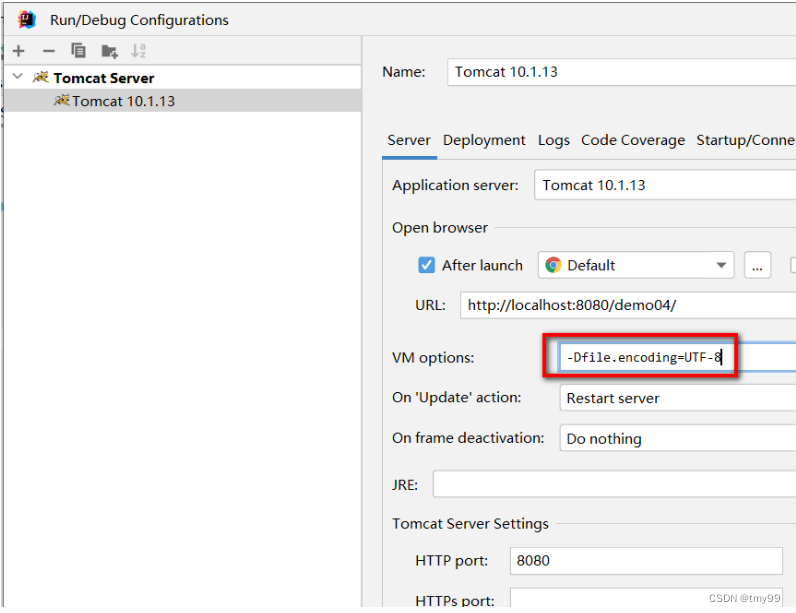
Javaweb基础-tomcat,servlet
一.配置文件基础: properties配置文件: 由键值对组成 键和值之间的符号是等号 每一行都必须顶格写,前面不能有空格之类的其他符号 xml配置文件:(xml语法HTML语法HTML约束)xml约束-DTD / Schema DOM4…...

HCIA-HarmonyOS设备开发认证V2.0-3.2.轻量系统内核基础-中断管理
目录 一、中断基础概念二、中断管理使用说明三、中断管理模块接口四、代码分析(待续...)坚持就有收获 一、中断基础概念 在程序运行过程中,出现需要由 CPU 立即处理的事务时,CPU 暂时中止当前程序的执行转而处理这个事务…...

【开源】JAVA+Vue+SpringBoot实现就医保险管理系统
目录 一、摘要1.1 项目介绍1.2 项目录屏 二、功能模块2.1 科室档案模块2.2 医生档案模块2.3 预约挂号模块2.4 我的挂号模块 三、系统展示四、核心代码4.1 用户查询全部医生4.2 新增医生4.3 查询科室4.4 新增号源4.5 预约号源 五、免责说明 一、摘要 1.1 项目介绍 基于JAVAVue…...

Stable Diffusion 模型下载:DreamShaper XL(梦想塑造者 XL)
本文收录于《AI绘画从入门到精通》专栏,专栏总目录:点这里。 文章目录 模型介绍生成案例案例一案例二案例三案例四案例五案例六案例七案例八案例九案例十 下载地址 模型介绍 DreamShaper 是一个分格多样的大模型,可以生成写实、原画、2.5D 等…...

【机器学习】数据清洗之处理异常点
🎈个人主页:甜美的江 🎉欢迎 👍点赞✍评论⭐收藏 🤗收录专栏:机器学习 🤝希望本文对您有所裨益,如有不足之处,欢迎在评论区提出指正,让我们共同学习、交流进步…...

JavaScript学习之旅10------掌握jQuery:实用应用案例深度解析
目录 写在开头1. jQuery基础知识回顾1.1. 选择器1.2. 事件1.3. 效果1.4. DOM操作1.5. AJAX 2. 实用应用案例分析2.1. 动态内容加载2.2. 表单验证2.3. 图像滑动门效果2.4. 创建动态导航菜单 3. 高级技巧与最佳实践3.1. 优化jQuery代码的性能3.2. jQuery插件的使用和自定义3.3. j…...

生成xcframework
打包 XCFramework 的方法 XCFramework 是苹果推出的一种多平台二进制分发格式,可以包含多个架构和平台的代码。打包 XCFramework 通常用于分发库或框架。 使用 Xcode 命令行工具打包 通过 xcodebuild 命令可以打包 XCFramework。确保项目已经配置好需要支持的平台…...

基于ASP.NET+ SQL Server实现(Web)医院信息管理系统
医院信息管理系统 1. 课程设计内容 在 visual studio 2017 平台上,开发一个“医院信息管理系统”Web 程序。 2. 课程设计目的 综合运用 c#.net 知识,在 vs 2017 平台上,进行 ASP.NET 应用程序和简易网站的开发;初步熟悉开发一…...

MongoDB学习和应用(高效的非关系型数据库)
一丶 MongoDB简介 对于社交类软件的功能,我们需要对它的功能特点进行分析: 数据量会随着用户数增大而增大读多写少价值较低非好友看不到其动态信息地理位置的查询… 针对以上特点进行分析各大存储工具: mysql:关系型数据库&am…...

在HarmonyOS ArkTS ArkUI-X 5.0及以上版本中,手势开发全攻略:
在 HarmonyOS 应用开发中,手势交互是连接用户与设备的核心纽带。ArkTS 框架提供了丰富的手势处理能力,既支持点击、长按、拖拽等基础单一手势的精细控制,也能通过多种绑定策略解决父子组件的手势竞争问题。本文将结合官方开发文档,…...

新能源汽车智慧充电桩管理方案:新能源充电桩散热问题及消防安全监管方案
随着新能源汽车的快速普及,充电桩作为核心配套设施,其安全性与可靠性备受关注。然而,在高温、高负荷运行环境下,充电桩的散热问题与消防安全隐患日益凸显,成为制约行业发展的关键瓶颈。 如何通过智慧化管理手段优化散…...

HBuilderX安装(uni-app和小程序开发)
下载HBuilderX 访问官方网站:https://www.dcloud.io/hbuilderx.html 根据您的操作系统选择合适版本: Windows版(推荐下载标准版) Windows系统安装步骤 运行安装程序: 双击下载的.exe安装文件 如果出现安全提示&…...

大模型多显卡多服务器并行计算方法与实践指南
一、分布式训练概述 大规模语言模型的训练通常需要分布式计算技术,以解决单机资源不足的问题。分布式训练主要分为两种模式: 数据并行:将数据分片到不同设备,每个设备拥有完整的模型副本 模型并行:将模型分割到不同设备,每个设备处理部分模型计算 现代大模型训练通常结合…...

HarmonyOS运动开发:如何用mpchart绘制运动配速图表
##鸿蒙核心技术##运动开发##Sensor Service Kit(传感器服务)# 前言 在运动类应用中,运动数据的可视化是提升用户体验的重要环节。通过直观的图表展示运动过程中的关键数据,如配速、距离、卡路里消耗等,用户可以更清晰…...

【Nginx】使用 Nginx+Lua 实现基于 IP 的访问频率限制
使用 NginxLua 实现基于 IP 的访问频率限制 在高并发场景下,限制某个 IP 的访问频率是非常重要的,可以有效防止恶意攻击或错误配置导致的服务宕机。以下是一个详细的实现方案,使用 Nginx 和 Lua 脚本结合 Redis 来实现基于 IP 的访问频率限制…...

【MATLAB代码】基于最大相关熵准则(MCC)的三维鲁棒卡尔曼滤波算法(MCC-KF),附源代码|订阅专栏后可直接查看
文章所述的代码实现了基于最大相关熵准则(MCC)的三维鲁棒卡尔曼滤波算法(MCC-KF),针对传感器观测数据中存在的脉冲型异常噪声问题,通过非线性加权机制提升滤波器的抗干扰能力。代码通过对比传统KF与MCC-KF在含异常值场景下的表现,验证了后者在状态估计鲁棒性方面的显著优…...
