2023-2-11 刷题情况
最短路计数
题目描述
给出一个 NNN 个顶点 MMM 条边的无向无权图,顶点编号为 1∼N1\sim N1∼N。问从顶点 111 开始,到其他每个点的最短路有几条。
输入格式
第一行包含 222 个正整数 N,MN,MN,M,为图的顶点数与边数。
接下来 MMM 行,每行 222 个正整数 x,yx,yx,y,表示有一条由顶点 xxx 连向顶点 yyy 的边,请注意可能有自环与重边。
输出格式
共 NNN 行,每行一个非负整数,第 iii 行输出从顶点 111 到顶点 iii 有多少条不同的最短路,由于答案有可能会很大,你只需要输出 $ ans \bmod 100003$ 后的结果即可。如果无法到达顶点 iii 则输出 000。
样例
样例输入
5 7
1 2
1 3
2 4
3 4
2 3
4 5
4 5
样例输出
1
1
1
2
4
提示
111 到 555 的最短路有 444 条,分别为 222 条 1→2→4→51\to 2\to 4\to 51→2→4→5 和 222 条 1→3→4→51\to 3\to 4\to 51→3→4→5(由于 4→54\to 54→5 的边有 222 条)。
- 对于 20%20\%20% 的数据,1≤N≤1001\le N \le 1001≤N≤100;
- 对于 60%60\%60% 的数据,1≤N≤1031\le N \le 10^31≤N≤103;
- 对于 100%100\%100% 的数据,1≤N≤1061\le N\le10^61≤N≤106,1≤M≤2×1061\le M\le 2\times 10^61≤M≤2×106。
思路
无向无权图。可使用bfs遍历,因为路径的权重都为1。
当前图中存在自环,但自环并不影响bfs遍历的最短路。
然后就是重边会对结果造成影响,需要我们考虑。
代码实现
import java.util.*;public class Main{static int MOD = (int)1e5 + 3;public static void main(String[] args){Scanner sc = new Scanner(System.in);int n = sc.nextInt(), len = sc.nextInt();List<Integer> list[] = new ArrayList[n+1];// 去环,已经进入过队列的结点,将不再进入队列boolean[] vis = new boolean[n+1];int[] depth = new int[n+1];// 结果。int[] ans = new int[n+1];for(int i = 1; i <= n; i++) list[i] = new ArrayList<>();int x, y;for (int i = 0; i < len; i++) {x = sc.nextInt();y = sc.nextInt();list[x].add(y);list[y].add(x);}Queue<Integer> queue = new ArrayDeque<>();depth[1] = 0;vis[1] = true;ans[1] = 1;queue.offer(1);while(!queue.isEmpty()){int cur = queue.poll();for(int next : list[cur]){if(!vis[next]){vis[next] = true;depth[next] = depth[cur] + 1;queue.offer(next);}// next结点,只有深度为 depth[next]的时候才会更新。// 换句话说就是只有第一次与第一次相同时间到达next时,才会更新值。if(depth[next] == depth[cur] + 1) ans[next] = (ans[next] + ans[cur]) % MOD;}}for(int i = 1; i <= n; i++) System.out.println(ans[i]);sc.close();}
}
中位数
题目描述
给出 1,2,...,n1,2,...,n1,2,...,n 的一个排列,统计该排列有多少个长度为奇数的连续子序列的中位数是 bbb。中位数是指把所有元素从小到大排列后,位于中间的数。
输入格式
第一行为两个正整数 nnn 和 bbb,第二行为 1,2,...,n1,2,...,n1,2,...,n 的排列。
输出格式
输出一个整数,即中位数为 bbb 的连续子序列个数。
样例
样例输入
7 4
5 7 2 4 3 1 6
样例输出
4
提示
数据规模与约定
-
对于 30%30\%30% 的数据中,满足 n≤100n \le 100n≤100;
-
对于 60%60\%60% 的数据中,满足 n≤1000n \le 1000n≤1000;
-
对于 100%100\%100% 的数据中,满足 n≤100000,1≤b≤nn \le 100000,1 \le b \le nn≤100000,1≤b≤n。
思路
因为满足需要的区间一定包含b, 所以我们可以先把b在数组中的位置找到。再到基础上拓展区间。
需要b成为区间的中位数,即是需要区间内大于b的数的数量等于区间内小于b的数的数量,我们可以把大于b的数记作1, 小于b的数记为-1。然后只需要左边区间加+右边区间 = 0即为找到一个区间。(还需要特别注意区间长度为奇数也是条件之一)
代码实现
import java.util.*;public class Main{public static void main(String[] args){Scanner sc = new Scanner(System.in);int n = sc.nextInt(), b = sc.nextInt();int[] arr = new int[n+1];for(int i = 1; i <= n; i++) arr[i] = sc.nextInt();int index = query(arr, b);HashMap<Integer, Integer> one = new HashMap<>();HashMap<Integer, Integer> two = new HashMap<>();two.put(0, 1);int val = 0;for(int i = index - 1; i > 0; i--){val += (arr[i] > b ? 1 : -1);if((index - i) % 2 == 1) one.put(val, one.getOrDefault(val, 0) + 1);else two.put(val, two.getOrDefault(val, 0) + 1);}val = 0;long ans = 0;for(int i = index; i <= n; i++){val += (arr[i] == b ? 0 : (arr[i] > b ? 1 : -1));if((i-index) % 2 == 1) ans += one.getOrDefault(-val, 0);else ans += two.getOrDefault(-val, 0);}System.out.println(ans);sc.close();}static int query(int[] arr, int b){for(int i = 1; i < arr.length; i++){if(arr[i] == b) return i; }return -1;}
}
相关文章:

2023-2-11 刷题情况
最短路计数 题目描述 给出一个 NNN 个顶点 MMM 条边的无向无权图,顶点编号为 1∼N1\sim N1∼N。问从顶点 111 开始,到其他每个点的最短路有几条。 输入格式 第一行包含 222 个正整数 N,MN,MN,M,为图的顶点数与边数。 接下来 MMM 行&…...

2019_41 考研408
2019年(单链表)41.(13分)设线性表采用带头结点的单链表保存,链表中的结点定义如下:typedef struct node {int data;struct node* next;}NODE;请设计一个空间复杂度为O(1)且时间上尽可能高效的算法,重新排列L中的各结点,得到线性表L(q,a,,a,an…...

Linux账号与用户组
目录 用户标识符:UID与GID 用户账号 /etc/passwd文件结构 1、账号名称 2、密码 3、UID 4、GID 5、用户信息说明栏 6、家目录 7、shell /etc/shadow文件结构 1、账号名称 2、密码 3、最近修改密码的日期 4、密码不可被修改的天数(与第三字…...
有趣的Hack-A-Sat黑掉卫星挑战赛——定位卫星Jackson
国家太空安全是国家安全在空间领域的表现。随着太空技术在政治、经济、军事、文化等各个领域的应用不断增加,太空已经成为国家赖以生存与发展的命脉之一,凝聚着巨大的国家利益,太空安全的重要性日益凸显[1]。而在信息化时代,太空安…...

JAVA集合专题3 —— vector + LinkedList + Set
目录vector的特点LinkedList底层结构模拟双向链表比较ArrayList和LinkedListSet接口基本介绍Set接口的遍历方式Set接口实现类对象的特点Set接口实现类HashSet模拟HashSet/HashMap的底层结构vector的特点 Vector底层是一个对象数组Vector是线程同步的,即线程安全的&…...

Scout:一款功能强大的轻量级URL模糊测试与爬取工具
关于Scout Scout是一款功能强大的轻量级URL模糊测试与爬取工具,可以帮助广大研究人员进行URL模糊测试,并爬取目标Web服务器中难以扫描发现的VHSOT、文件和目录等资源。 项目中包含了一个完整的字典文件,并尽可能地提供了更多的便携性&#…...

leaflet 解决marker呈现灰色边框的问题
第052个 点击查看专栏目录 本示例的目的是介绍演示如何在vue+leaflet示例中处理marker外面有灰色边框的问题,请看未处理会后的图片。 处理后的结果非常满意,不再显示灰色边框。处理方法参考源代码。 直接复制下面的 vue+openlayers源代码,操作2分钟即可运行实现效果; 注意…...

MySQL JSON类型字段的查找与更新
MySQL 提供了丰富的函数用于 JSON 类型字段的查找与更新,详见官方文档。 创建一个表 t1,basic_info 字段为JSON类型: CREATE TABLE t1 (id int(11) NOT NULL AUTO_INCREMENT,basic_info json DEFAULT NULL,PRIMARY KEY (id) ) ENGINEInnoDB DEFAULT CH…...

element Ui树状图控件 spring boot Vue 实现角色授权功能
目录 前言: 二. element ui 2.1官网提供的核心代码 三.表结构 编辑 四.后端 4.1功能分析 4.2实体类 4.3 查询全部权限显示的结果 4.2修改角色权限的后台方法 五.vue 5.0代码总览 5.1树形图 5.2所需要的绑定数据 5.3所需方法 前言: 先上图…...

已解决sc delete MongoDB卸载MongoDB拒绝访问。
已解决sc delete MongoDB卸载MongoDB拒绝访问。 文章目录报错问题报错翻译报错原因解决方法联系博主免费帮忙解决报错报错问题 粉丝群里面的一个小伙伴遇到问题跑来私信我,想卸载MongoDB数据库,但是发生了报错(当时他心里瞬间凉了一大截&…...

python的opencv操作记录11——阈值分割
文章目录传统图像处理分割阈值分割一个应用场景opencv库中的阈值分割固定阈值THRESH_OTSU 大津法阈值自适应阈值传统图像处理分割 现在提到图像分割,很多人会直接想到当前火爆的深度学习的各种分割网络,比如实例分割,语义分割等。其实在传统…...
Python-项目实战--飞机大战-英雄登场(7)
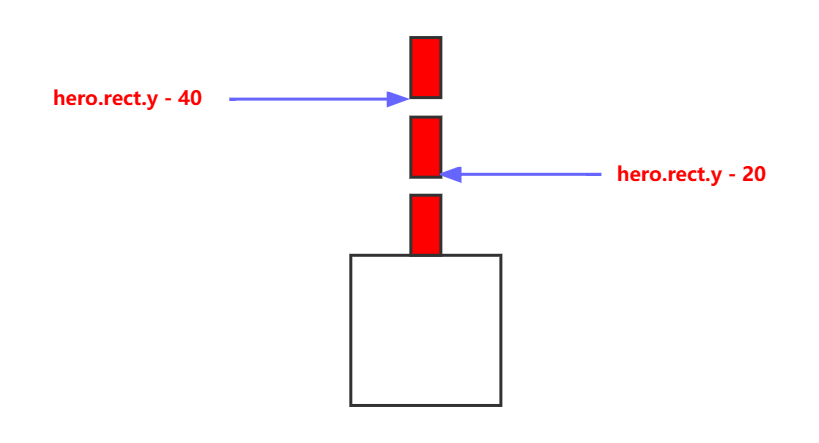
目标设计英雄和子弹类使用pygame.key.get_pressed()移动英雄发射子弹1.设计英雄和子弹类1.1英雄需求游戏启动后,英雄出现在屏幕的水平中间位置,距离屏幕底部120像素英雄每隔0.5秒发射一次子弹,每次连发三枚子弹英雄默认不会移动,需…...
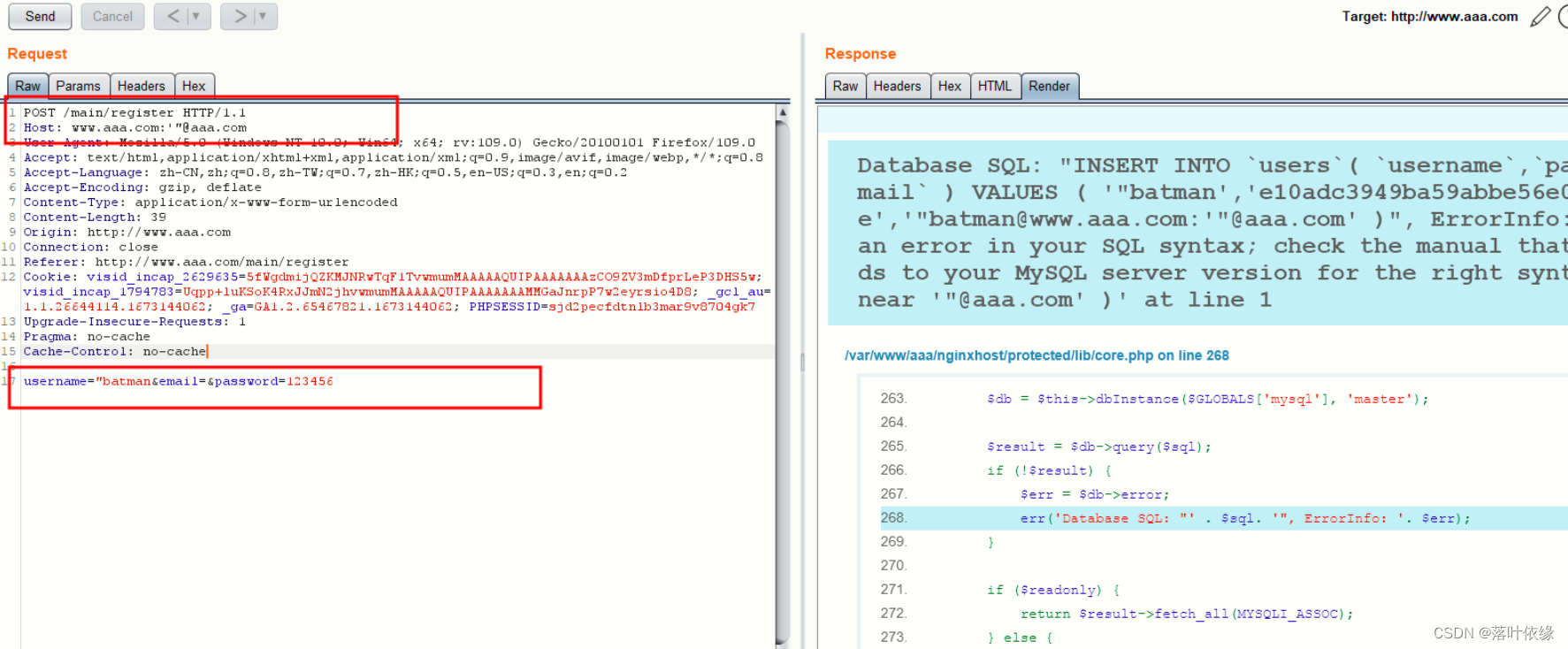
寒假安全作业nginx-host绕过实例复现
1.测试环境搭建 LNMP架构的话,肯定就是linux、nginx、mysql、php四大组件。在后面的复现中我们还会用到https的一部分知识,故这里的nginx就需要使用虚拟主机并且配置https证书,且具有php解析功能。 1.1 基础nginx配置 #1.创建web目录 mkdir …...
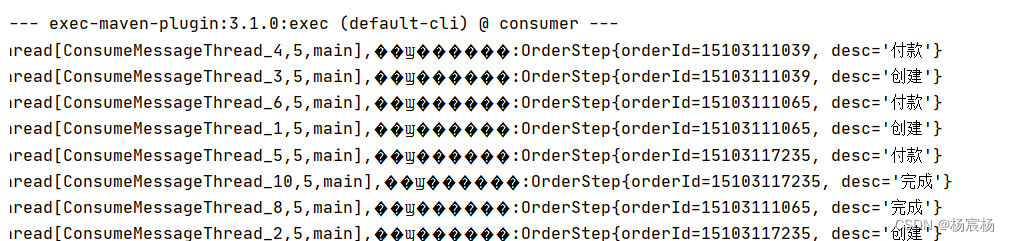
RocketMQ-消息消费模式 顺序消费
RocketMQ-消息消费模式 顺序消费RocketMQ-消息消费模式集群模式集群模式的演示(本身就默认)Rocketmq存储队列广播模式顺序消费如何改实现顺序消费RocketMQ-消息消费模式 集群模式 在消费模式为集群的情况下,如果机器是集群的,消息只会给集群中的其中一台机器消费到 集群模…...
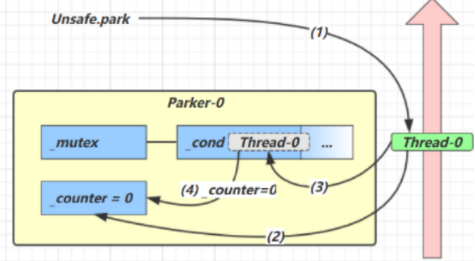
一、Java并发编程之线程、synchronized
黑马课程 文章目录1. Java线程1.1 创建和运行线程方法一:Thread方法二:Runnable(推荐)lambda精简Thread和runnable原理方法三:FutureTask配合Thread1.2 查看进程和线程的方法1.3 线程运行原理栈与栈帧线程上下文切换1.…...
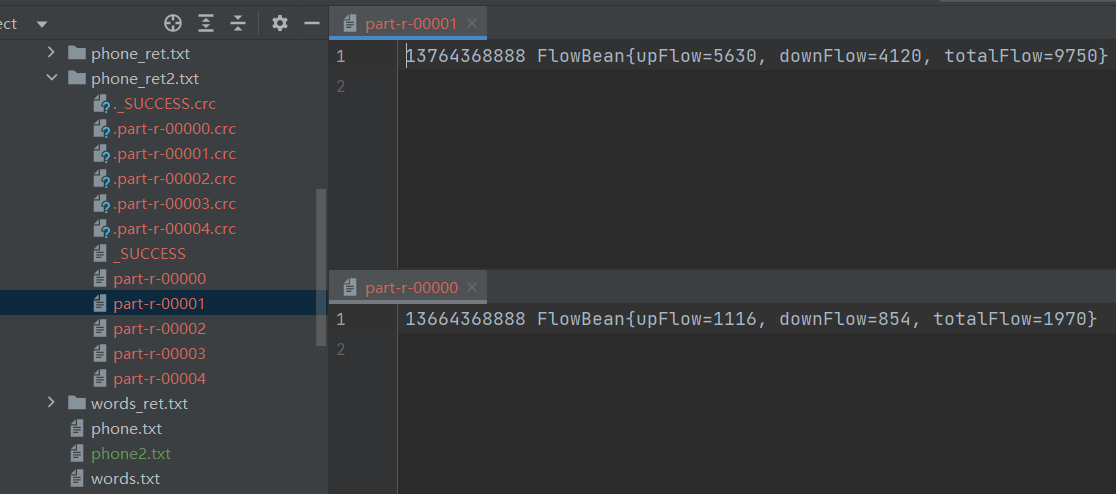
12.hadoop系列之MapReduce分区实践
本文我们学习MapReduce默认分区以及自定义分区实践 当我们要求将统计结果按照条件输出到不同文件(分区),比如按照统计结果将手机归属地不同省份输出到不同文件中(分区) 1.默认Partitioner分区 public class HashPartitioner<K, V> extends Partitioner<…...
有了独自开,一个人就是一个团队
文章目录 简单介绍优点 优秀案例平台福利总结 简单介绍 独自开是一个基于商品与服务交易全流程的PaaS开发平台。对于开发者,独自开可以协助开发者一个人独自开发一套系统。 优点 独自开有独创的分层标准化平台架构,可以满足系统的任何个性化需求。 …...

web期末复习 2023.02.11
文章目录Web 的概念Web 组成用户通过浏览器请求资源的过程:HTML 超文本标记语言CSS插入样式表的方法有三种:对象,类,实例一个完整的 JavaScript 实现是由以下 3 个不同部分组成的:JavaScript 用法什么是 Java Server Pages?JSP 注释JSP 的 J…...

第44章 用户密码实体及其约束规则的定义实现
1 说明: 由当前程序需要兼容实现多种用户密码的加密操作,所以必须把“CustomerPassword”定义为实体类,该类用于用于把加密方式、密钥及其加密后的密码持久化到“CustomerPassword”表中,以便用为用户登录操作提供验证支撑。 如果…...

聊聊并发与锁
持续坚持原创输出,点击蓝字关注我吧1.并发与并行并发可以充分地利用 CPU 资源,一般都会使用多线程实现。多线程的作用是提高任务的平均执行速度,但是会导致程序可理解性变差,编程难度加大。关于对并发与并行的概念,大家…...

FFmpeg 低延迟同屏方案
引言 在实时互动需求激增的当下,无论是在线教育中的师生同屏演示、远程办公的屏幕共享协作,还是游戏直播的画面实时传输,低延迟同屏已成为保障用户体验的核心指标。FFmpeg 作为一款功能强大的多媒体框架,凭借其灵活的编解码、数据…...

遍历 Map 类型集合的方法汇总
1 方法一 先用方法 keySet() 获取集合中的所有键。再通过 gey(key) 方法用对应键获取值 import java.util.HashMap; import java.util.Set;public class Test {public static void main(String[] args) {HashMap hashMap new HashMap();hashMap.put("语文",99);has…...

Ascend NPU上适配Step-Audio模型
1 概述 1.1 简述 Step-Audio 是业界首个集语音理解与生成控制一体化的产品级开源实时语音对话系统,支持多语言对话(如 中文,英文,日语),语音情感(如 开心,悲伤)&#x…...

爬虫基础学习day2
# 爬虫设计领域 工商:企查查、天眼查短视频:抖音、快手、西瓜 ---> 飞瓜电商:京东、淘宝、聚美优品、亚马逊 ---> 分析店铺经营决策标题、排名航空:抓取所有航空公司价格 ---> 去哪儿自媒体:采集自媒体数据进…...

【JVM】Java虚拟机(二)——垃圾回收
目录 一、如何判断对象可以回收 (一)引用计数法 (二)可达性分析算法 二、垃圾回收算法 (一)标记清除 (二)标记整理 (三)复制 (四ÿ…...

负载均衡器》》LVS、Nginx、HAproxy 区别
虚拟主机 先4,后7...

__VUE_PROD_HYDRATION_MISMATCH_DETAILS__ is not explicitly defined.
这个警告表明您在使用Vue的esm-bundler构建版本时,未明确定义编译时特性标志。以下是详细解释和解决方案: 问题原因: 该标志是Vue 3.4引入的编译时特性标志,用于控制生产环境下SSR水合不匹配错误的详细报告1使用esm-bundler…...

Ray框架:分布式AI训练与调参实践
Ray框架:分布式AI训练与调参实践 系统化学习人工智能网站(收藏):https://www.captainbed.cn/flu 文章目录 Ray框架:分布式AI训练与调参实践摘要引言框架架构解析1. 核心组件设计2. 关键技术实现2.1 动态资源调度2.2 …...

可下载旧版app屏蔽更新的app市场
软件介绍 手机用久了,app越来越臃肿,老手机卡顿成常态。这里给大家推荐个改善老手机使用体验的方法,还能帮我们卸载不需要的app。 手机现状 如今的app不断更新,看似在优化,实则内存占用越来越大,对手机性…...

Linux——TCP和UDP
一、TCP协议 1.特点 TCP提供的是面向连接、可靠的、字节流服务。 2.编程流程 (1)服务器端的编程流程 ①socket() 方法创建套接字 ②bind()方法指定套接字使用的IP地址和端口。 ③listen()方法用来创建监听队列。 ④accept()方法处理客户端的连接…...
