飞行路线(分层图+dijstra+堆优化)(加上题目选数复习)
飞行路线
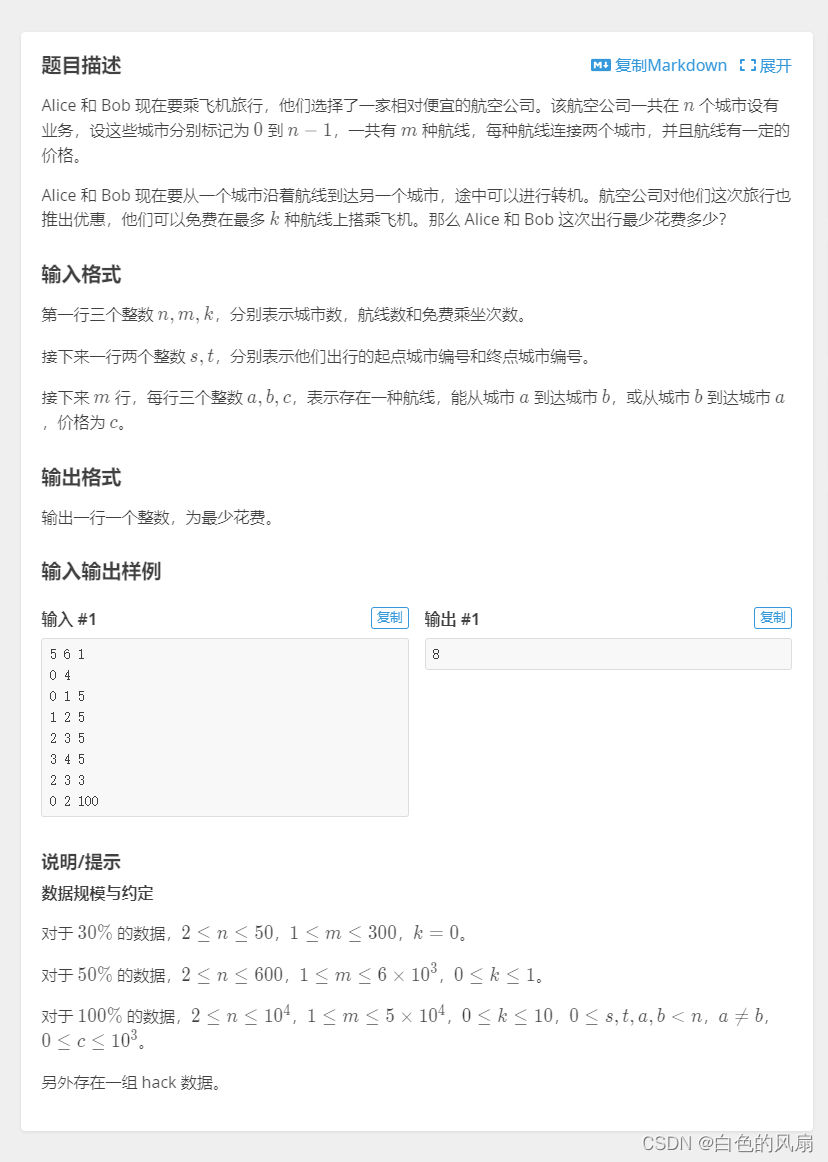
这一题除了堆优化和dijstra算法和链式前向星除外还多考了一个考点就是,分层图,啥叫分层图呢?简而言之就是一个三维的图,按照其题意来说有几个可以免费的点就有几层,而且这个分层的权值为0(这样就相当于免费了), 怎么来理解这个意思呢?就是相当于这个dijstra算法它遍历的不再是一个一维图而是一个三维图,本质还是一样的,由于我们储存的边信息用的是链式前向星,所有所有的边都是按照顺序结构存放在一个一个顺序表中,所以我们不用担心空间复杂度的问题,只需要担心时间复杂度,但是由于我们用到了对堆优化。这一题就是相当于将前面的堆优化就上dijstra算法加上链式前向星重新复习一遍。
代码如下
#include<iostream>
#include<queue>
#include<string.h>
using namespace std;
const int M = 2e5;
const int N = 5e6;
int ans[N], cnt = 0, head[N], s, t, n, m, k;
bool vis[N];
//优先队列的结构体
struct node {int id;int dis;bool operator< (const node& x) const {return x.dis < dis;}
};
//优先队列
priority_queue<node> q;
//边的结构体
struct EDGE
{int next;int w;int to;
}e[N];
//键边函数
void add(int u, int v, int w)
{e[++cnt].w = w;e[cnt].to = v;e[cnt].next = head[u];head[u] = cnt;
}
//dijstra函数
void dijstra()
{ans[s] = 0;q.push(node{ s,0 });while (!q.empty()){node tmp = q.top();q.pop();int k = tmp.id;if (vis[k])continue;vis[k] = true;for (int i = head[k]; i != 0; i = e[i].next){int to = e[i].to;if (!vis[to] && ans[to] > ans[k] + e[i].w){ans[to] = ans[k] + e[i].w;q.push(node{ to,ans[to] });}}}
}int main()
{cin >> n >> m >> k;cin >> s >> t;s++;t++;memset(ans, 0x3f, sizeof(ans));for (int i = 1; i <= m; i++){int u, v, w;cin >> u >> v >> w;++u;++v;add(u, v, w);add(v, u, w);for (int j = 1; j <= k; j++) {add(u + (j - 1) * n, v + j * n, 0);add(v + (j - 1) * n, u + j * n, 0);add(v + j * n, u + j * n, w);add(u + j * n, v + j * n, w);}}dijstra();int anss = 0x7fffffff;for (int i = 0; i <= k; i++){if (anss > ans[t + i * n]){anss = ans[t + i * n];}}cout << anss << endl;return 0;
}选数
为什么要重新写一下这一题,因为我在这题错过两遍了,为了防止错三遍 ,再写一遍,结果终于是在没有外力靠住下写出来了
主要思路还是深搜:在dfs函数中需要定义三个变量,第一是就是一记录有多少个答案,第二就是就是for循环的下标,第三就是sum用于记录这个和。
代码如下(我竟然真的靠自己完全写出来的)
#include<iostream>
#include<queue>
#include<algorithm>
#include<cmath>
using namespace std;
int n,m;
int a[100000];
bool ispear(int x)
{if(x==1)return false;if(x==2)return true;if(x>3){for(int i=2;i<=sqrt(x);i++){if(x%i==0)return false;}}return true;
}
int ans=0;
void dfs(int sum,int step,int cnt)
{if(cnt>=m){if(ispear(sum)){ans++;}return ;}for(int i=step+1;i<=n;i++){dfs(sum+a[i],i,cnt+1);}
}
int main()
{cin>>n>>m;for(int i=1;i<=n;i++)cin>>a[i];dfs(0,0,0);cout<<ans<<endl;return 0;
}相关文章:

飞行路线(分层图+dijstra+堆优化)(加上题目选数复习)
飞行路线 这一题除了堆优化和dijstra算法和链式前向星除外还多考了一个考点就是,分层图,啥叫分层图呢?简而言之就是一个三维的图,按照其题意来说有几个可以免费的点就有几层,而且这个分层的权值为0(这样就相…...
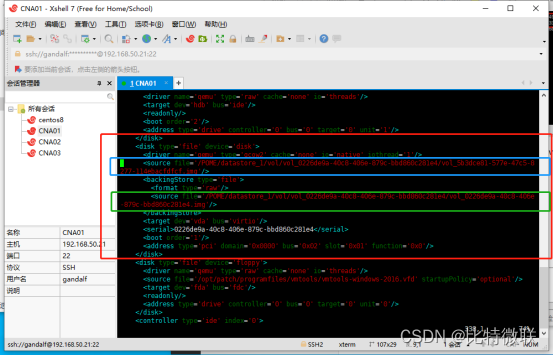
云计算基础-快照与克隆
快照及克隆 什么是快照 快照是数据存储的某一时刻的状态记录,也就是把虚拟机当前的状态保存下来(快照不是备份,快照保存的是状态,备份保存的是副本) 快照优点 速度快,占用空间小 快照工作原理 在了解快照原理前,…...

使用 RAG 创建 LLM 应用程序
如果您考虑为您的文件或网站制作一个能够回应您的个性化机器人,那么您来对地方了。我可以帮助您使用Langchain和RAG策略来创建这样一个机器人。 了解ChatGPT的局限性和LLMs ChatGPT和其他大型语言模型(LLMs)经过广泛训练,以理解…...
第13章 网络 Page744~746 asio核心类 ip::tcp::endPoint
2. ip::tcp::endpoint ip::tcp::socket用于连接TCP服务端的 async_connect()方法的第一个入参是const endpoint_type& peer_endpoint. 此处的类型 endpoint_type 是 ip::tcp::endpoint 在 在 ip::tcp::socket 类内部的一个别名。 libucurl 库采用字符串URL表达目标的地…...

面试浏览器框架八股文十问十答第一期
面试浏览器框架八股文十问十答第一期 作者:程序员小白条,个人博客 相信看了本文后,对你的面试是有一定帮助的!关注专栏后就能收到持续更新! ⭐点赞⭐收藏⭐不迷路!⭐ 1)什么是 XSS 攻击&#…...
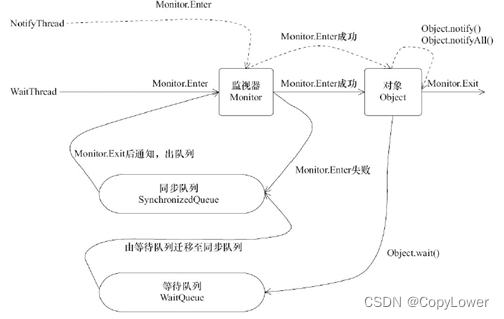
多线程的基本原理学习
由一个问题引发的思考 线程的合理使用能够提升程序的处理性能,主要有两个方面,第一个是能够利用多核cpu以及超线程技术来实现线程的并行执行;第二个是线程的异步化执行相比于同步执行来说,异步执行能够很好的优化程序的处理性能提…...

C/C++进制转换
十进制转化为二进制 进制转化#include <iostream> using namespace std;void change(int); int main() {int num;cout << "请输入一个十进制数: ";cin >> num;cout << "转化后的二进制数为: ";change(num);return 0; } void chan…...
使用 Coze 搭建 TiDB 助手
导读 本文介绍了使用 Coze 平台搭建 TiDB 文档助手的过程。通过比较不同 AI Bot 平台,突出了 Coze 在插件能力和易用性方面的优势。文章深入讨论了实现原理,包括知识库、function call、embedding 模型等关键概念,最后成功演示了如何在 Coze…...

Arduino程序简单入门
文章目录 一、结构1.1 setup()1.2 loop() 二、结构控制2.1 if2.2 if...else2.3 switch case2.4 for2.5 while2.6 do...while2.7 break2.8 continue2.9 return2.10 goto 三、扩展语法3.1 ;(分号)3.2 {}(花括号)3.3 //(单…...
)
QT+OSG/osgEarth编译之八十三:osgdb_ogr+Qt编译(一套代码、一套框架,跨平台编译,版本:OSG-3.6.5插件库osgdb_ogr)
文章目录 一、osgdb_ogr介绍二、文件分析三、pro文件四、编译实践一、osgdb_ogr介绍 osgDB是OpenSceneGraph(OSG)库中的一个模块,用于加载和保存3D场景数据。osgDB_ogr是osgDB模块中的一个插件,它提供了对OGR(开放地理空间联盟)库的支持。 OGR是一个开源的地理空间数据…...

开年炸裂-Sora/Gemini
最新人工智能消息 谷歌的新 Gemini 模型 支持多达 1M的Token,可以分析长达一小时的视频 1M Token可能意味着分析700,000 个单词、 30,000 行代码或11 小时的音频、总结、改写和引用内容。 Comment:google公司有夸大的传统,所以真实效果需要上…...
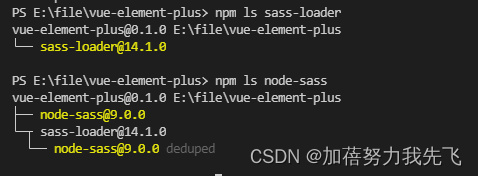
vue前端系统启动报错Module not found: Error: Can‘t resolve ‘sass-loader‘
1、确认项目中是否已安装 node-sass 包。sass-loader 是依赖于 node-sass 包的,如果没有安装 node-sass 包,也会导致无法找到 sass-loader 包。 npm ls node-sass安装 node-sass 包: npm install --save-dev node-sass2、确认项目中是否已安…...

HTML | DOM | 网页前端 | 常见HTML标签总结
文章目录 1.前端开发简单分类2.前端开发环境配置3.HTML的简单介绍4.常用的HTML标签介绍 1.前端开发简单分类 前端开发,这里是一个广义的概念,不单指网页开发,它的常见分类 网页开发:前端开发的主要领域,使用HTML、CS…...

乡政府|乡政府管理系统|基于Springboot的乡政府管理系统设计与实现(源码+数据库+文档)
乡政府管理系统目录 目录 基于Springboot的乡政府管理系统设计与实现 一、前言 二、系统功能设计 三、系统实现 1、用户信息管理 2、活动信息管理 3、新闻类型管理 4、新闻动态管理 四、数据库设计 1、实体ER图 五、核心代码 六、论文参考 七、最新计算机毕设选题推…...

存储系统如何规避数据静默错误SDC?
存储系统规避数据静默错误(Silent Data Corruption, SDC)是一项复杂且关键的任务,涉及多个层次的技术和策略。数据静默错误是指在存储或传输过程中发生的错误,这些错误未被检测出来,因此无法立即纠正,可能导…...

《Linux 简易速速上手小册》第8章: 安全性与加固(2024 最新版)
文章目录 8.1 防火墙与安全策略8.1.1 重点基础知识8.1.2 重点案例:配置 iptables 以保护 Web 服务器8.1.3 拓展案例 1:使用 firewalld 配置动态防御区域8.1.4 拓展案例 2:配置 ufw 以简化管理 8.2 SSH 安全最佳实践8.2.1 重点基础知识8.2.2 重…...
Ubuntu Desktop 显示文件路径
Ubuntu Desktop 显示文件路径 1. GUI hot key2. CLIReferences 1. GUI hot key Ctrl L: 显示文件路径 2. CLI right click -> Open in Terminal -> pwd strongforeverstrong:~/Desktop$ pwd /home/strong/DesktopReferences [1] Yongqiang Cheng, https://yongqiang…...
【Java程序设计】【C00270】基于Springboot的moba类游戏攻略分享平台(有论文)
基于Springboot的moba类游戏攻略分享平台(有论文) 项目简介项目获取开发环境项目技术运行截图 项目简介 这是一个基于Springboot的游戏攻略分享平台 本系统分为系统功能模块、管理员功能模块、以及用户后台功能模块。 系统功能模块:在平台首…...

【旧文更新】【优秀毕设】人脸识别打卡/签到/考勤管理系统(OpenCV+最简基本库开发、可移植树莓派 扩展网络图像推流控制 验证码及Excel邮件发送等功能)
【旧文更新】【优秀毕设】人脸识别打卡/签到/考勤管理系统(OpenCV最简基本库开发、可移植树莓派 扩展网络图像推流控制 验证码及Excel邮件发送等功能) 文章目录 关于旧文新发毕设结构主页面验证码识别效果管理页面人脸信息采集管理实时数据更新签到结果…...
模型 4i(趣味、利益、互动、个性)理论
系列文章 分享 模型,了解更多👉 模型_总纲目录。重在提升认知。以用户为中心营销。 1 模型 4i(趣味、利益、互动、个性)理论的应用 1.1 4i理论在电子商务中的应用 小米公司在其电子商务平台上运用了 4i理论,取得了较好的效果。具体表现如下…...

RocketMQ延迟消息机制
两种延迟消息 RocketMQ中提供了两种延迟消息机制 指定固定的延迟级别 通过在Message中设定一个MessageDelayLevel参数,对应18个预设的延迟级别指定时间点的延迟级别 通过在Message中设定一个DeliverTimeMS指定一个Long类型表示的具体时间点。到了时间点后…...

C++:std::is_convertible
C++标志库中提供is_convertible,可以测试一种类型是否可以转换为另一只类型: template <class From, class To> struct is_convertible; 使用举例: #include <iostream> #include <string>using namespace std;struct A { }; struct B : A { };int main…...

Linux相关概念和易错知识点(42)(TCP的连接管理、可靠性、面临复杂网络的处理)
目录 1.TCP的连接管理机制(1)三次握手①握手过程②对握手过程的理解 (2)四次挥手(3)握手和挥手的触发(4)状态切换①挥手过程中状态的切换②握手过程中状态的切换 2.TCP的可靠性&…...

大数据零基础学习day1之环境准备和大数据初步理解
学习大数据会使用到多台Linux服务器。 一、环境准备 1、VMware 基于VMware构建Linux虚拟机 是大数据从业者或者IT从业者的必备技能之一也是成本低廉的方案 所以VMware虚拟机方案是必须要学习的。 (1)设置网关 打开VMware虚拟机,点击编辑…...

vue3 字体颜色设置的多种方式
在Vue 3中设置字体颜色可以通过多种方式实现,这取决于你是想在组件内部直接设置,还是在CSS/SCSS/LESS等样式文件中定义。以下是几种常见的方法: 1. 内联样式 你可以直接在模板中使用style绑定来设置字体颜色。 <template><div :s…...

基础测试工具使用经验
背景 vtune,perf, nsight system等基础测试工具,都是用过的,但是没有记录,都逐渐忘了。所以写这篇博客总结记录一下,只要以后发现新的用法,就记得来编辑补充一下 perf 比较基础的用法: 先改这…...

Mac软件卸载指南,简单易懂!
刚和Adobe分手,它却总在Library里给你写"回忆录"?卸载的Final Cut Pro像电子幽灵般阴魂不散?总是会有残留文件,别慌!这份Mac软件卸载指南,将用最硬核的方式教你"数字分手术"࿰…...

反射获取方法和属性
Java反射获取方法 在Java中,反射(Reflection)是一种强大的机制,允许程序在运行时访问和操作类的内部属性和方法。通过反射,可以动态地创建对象、调用方法、改变属性值,这在很多Java框架中如Spring和Hiberna…...
基础光照(Basic Lighting))
C++.OpenGL (10/64)基础光照(Basic Lighting)
基础光照(Basic Lighting) 冯氏光照模型(Phong Lighting Model) #mermaid-svg-GLdskXwWINxNGHso {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-GLdskXwWINxNGHso .error-icon{fill:#552222;}#mermaid-svg-GLd…...

大学生职业发展与就业创业指导教学评价
这里是引用 作为软工2203/2204班的学生,我们非常感谢您在《大学生职业发展与就业创业指导》课程中的悉心教导。这门课程对我们即将面临实习和就业的工科学生来说至关重要,而您认真负责的教学态度,让课程的每一部分都充满了实用价值。 尤其让我…...
