代码随想录算法训练营第50天(动态规划07 ● 70. 爬楼梯 (进阶) ● 322. 零钱兑换 ● 279.完全平方数
动态规划part07
- 70. 爬楼梯 (进阶)
- 解题思路
- 总结
- 322. 零钱兑换
- 解题思路
- 总结
- 279.完全平方数
- 解题思路
70. 爬楼梯 (进阶)
这道题目 爬楼梯之前我们做过,这次再用完全背包的思路来分析一遍
文章讲解: 70. 爬楼梯 (进阶)
解题思路
我们之前做的 爬楼梯 是只能至多爬两个台阶。
这次改为:一步一个台阶,两个台阶,三个台阶,…,直到 m个台阶。问有多少种不同的方法可以爬到楼顶呢?
这又有难度了,这其实是一个完全背包问题。
1阶,2阶,.... m阶就是物品,楼顶就是背包。
每一阶可以重复使用,例如跳了1阶,还可以继续跳1阶。
问跳到楼顶有几种方法其实就是问装满背包有几种方法。
此时大家应该发现这就是一个完全背包问题了!
和题目动态规划:377. 组合总和 Ⅳ基本就是一道题了。
import java.util.Scanner;
class climbStairs{public static void main(String [] args){Scanner sc = new Scanner(System.in);int m, n;while (sc.hasNextInt()) {// 从键盘输入参数,中间用空格隔开n = sc.nextInt();m = sc.nextInt();// 求排列问题,先遍历背包再遍历物品int[] dp = new int[n + 1];dp[0] = 1;for (int j = 1; j <= n; j++) {for (int i = 1; i <= m; i++) {if (j - i >= 0) dp[j] += dp[j - i];}}System.out.println(dp[n]);}}
}
总结
本题看起来是一道简单题目,稍稍进阶一下其实就是一个完全背包!
如果我来面试的话,我就会先给候选人出一个 本题原题,看其表现,如果顺利写出来,进而在要求每次可以爬[1 - m]个台阶应该怎么写。
顺便再考察一下两个for循环的嵌套顺序,为什么target放外面,nums放里面。
这就能考察对背包问题本质的掌握程度,候选人是不是刷题背公式,一眼就看出来了。
这么一连套下来,如果候选人都能答出来,相信任何一位面试官都是非常满意的。
本题代码不长,题目也很普通,但稍稍一进阶就可以考察完全背包,而且题目进阶的内容在leetcode上并没有原题,一定程度上就可以排除掉刷题党了,简直是面试题目的绝佳选择!
322. 零钱兑换
如果求组合数就是外层for循环遍历物品,内层for遍历背包。
如果求排列数就是外层for遍历背包,内层for循环遍历物品。
这句话结合本题 大家要好好理解。
题目链接: 322. 零钱兑换
视频讲解: 322. 零钱兑换
文章讲解: 322. 零钱兑换
解题思路
题目中说每种硬币的数量是无限的,可以看出是典型的完全背包问题
动规五部曲分析如下:
- 确定dp数组以及下标的含义
dp[j]:凑足总额为j所需钱币的最少个数为dp[j] - 确定递推公式
递推公式:dp[j] = min(dp[j - coins[i]] + 1, dp[j]); - dp数组如何初始化
首先凑足总金额为0所需钱币的个数一定是0,那么dp[0] = 0;
考虑到递推公式的特性,dp[j]必须初始化为一个最大的数,否则就会在min(dp[j - coins[i]] + 1, dp[j])比较的过程中被初始值覆盖。
所以下标非0的元素都是应该是最大值。 - 确定遍历顺序
本题求钱币最小个数,那么钱币有顺序和没有顺序都可以,都不影响钱币的最小个数。
所以本题并不强调集合是组合还是排列。 - 举例推导dp数组
总结
动态规划:518.零钱兑换II 中求的是组合数,动态规划:377. 组合总和 Ⅳ 中求的是排列数。
而本题是要求最少硬币数量,硬币是组合数还是排列数都无所谓!所以两个for循环先后顺序怎样都可以!
// 动态规划 完全背包
class Solution {public int coinChange(int[] coins, int amount) {int max = Integer.MAX_VALUE;int[] dp = new int[amount + 1];//初始化dp数组为最大值for(int j = 0; j < dp.length; j++){dp[j] = max;}// 当金额为0时需要的硬币数目为0dp[0] = 0;for(int i = 0; i < coins.length; i++){//正序遍历:完全背包每个硬币可以选择多次for(int j = coins[i]; j <= amount; j++){if(dp[j - coins[i]] != max){// 选择硬币数目最小的情况dp[j] = Math.min(dp[j], dp[j - coins[i]] + 1);}}}return dp[amount] == max ? -1 : dp[amount];}
}
279.完全平方数
本题 和 322. 零钱兑换 基本是一样的,大家先自己尝试做一做
题目链接: 279.完全平方数
视频讲解: 279.完全平方数
文章讲解: 279.完全平方数
解题思路
和昨天的题目动态规划:322. 零钱兑换 是一样一样的!
class Solution {// 版本一,先遍历物品, 再遍历背包public int numSquares(int n) {int max = Integer.MAX_VALUE;int[] dp = new int[n + 1];//初始化for (int j = 0; j <= n; j++) {dp[j] = max;}//如果不想要寫for-loop填充數組的話,也可以用JAVA內建的Arrays.fill()函數。//Arrays.fill(dp, Integer.MAX_VALUE);//当和为0时,组合的个数为0dp[0] = 0;// 遍历物品for (int i = 1; i * i <= n; i++) {// 遍历背包for (int j = i * i; j <= n; j++) {//if (dp[j - i * i] != max) {dp[j] = Math.min(dp[j], dp[j - i * i] + 1);//}//不需要這個if statement,因爲在完全平方數這一題不會有"湊不成"的狀況發生( 一定可以用"1"來組成任何一個n),故comment掉這個if statement。}}return dp[n];}
}
相关文章:
 ● 322. 零钱兑换 ● 279.完全平方数)
代码随想录算法训练营第50天(动态规划07 ● 70. 爬楼梯 (进阶) ● 322. 零钱兑换 ● 279.完全平方数
动态规划part07 70. 爬楼梯 (进阶)解题思路总结 322. 零钱兑换解题思路总结 279.完全平方数解题思路 70. 爬楼梯 (进阶) 这道题目 爬楼梯之前我们做过,这次再用完全背包的思路来分析一遍 文章讲解: 70. 爬…...
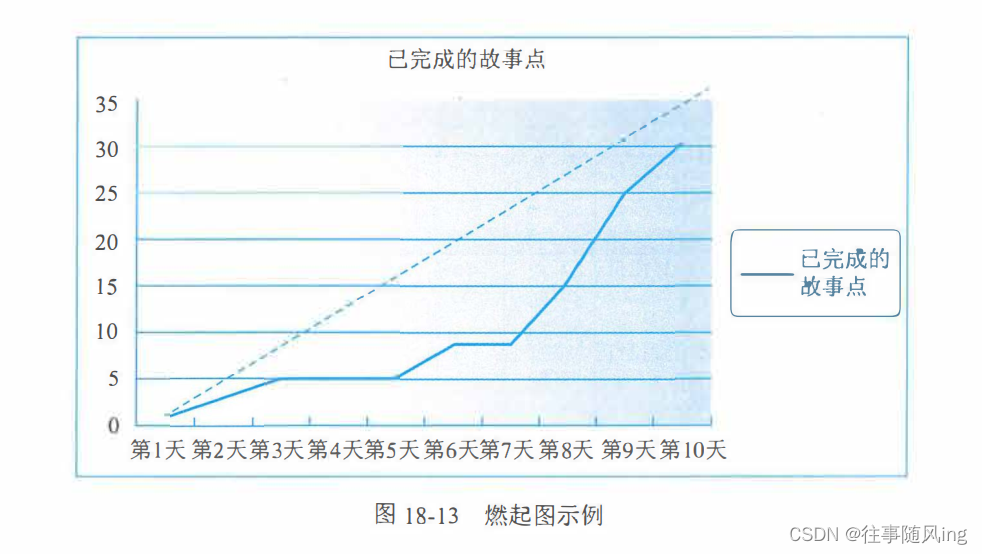
【软考问题】-- 13 - 知识精讲 - 项目绩效域管理
一、基本问题 问题1:干系人绩效域的预期目标主要包含什么? ①与干系人建立高效的工作关系;②干系人认同项目目标;③支持项目的干系人提高了满意度,并从中收益;④反对项目的干系人没有对项目产生负面影响。问…...
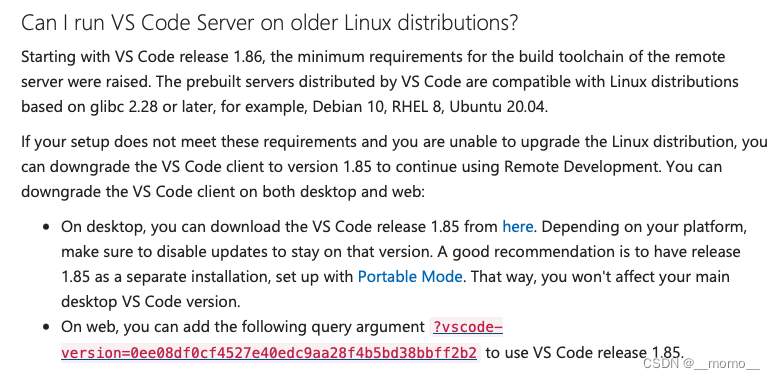
VSCode无法连接远程服务器的两种解决方法
文章目录 VSCode Terminal 报错解决方式1解决方式2you are connected to an OS version that is unsupported by Visual Studio Code解决方法 VSCode Terminal 报错 直接在terminal或cmd中使用ssh命令可以连接服务器,但是在vscode中存在报错,最后一行为…...
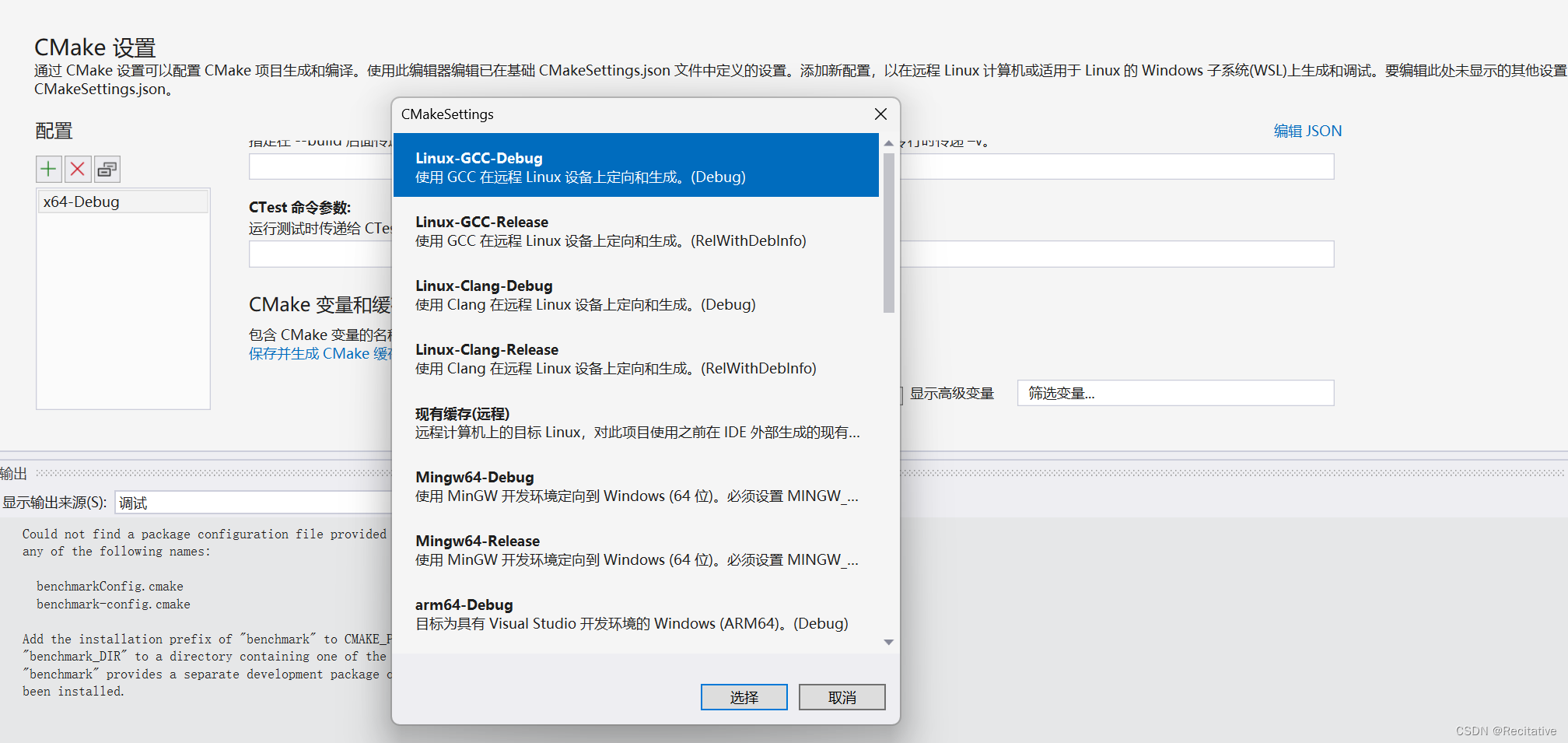
【Kuiperinfer】笔记01 项目预览与环境配置
学习目标 实现一个深度学习推理框架设计、编写一个计算图实现常见的算子,例如卷积、池化、全连接学会如何进行算子的优化加速使用自己的推理框架推理常见模型,检查结果是否能够和torch对齐 什么是推理框架? 推理框架用于对已经训练完成的模…...
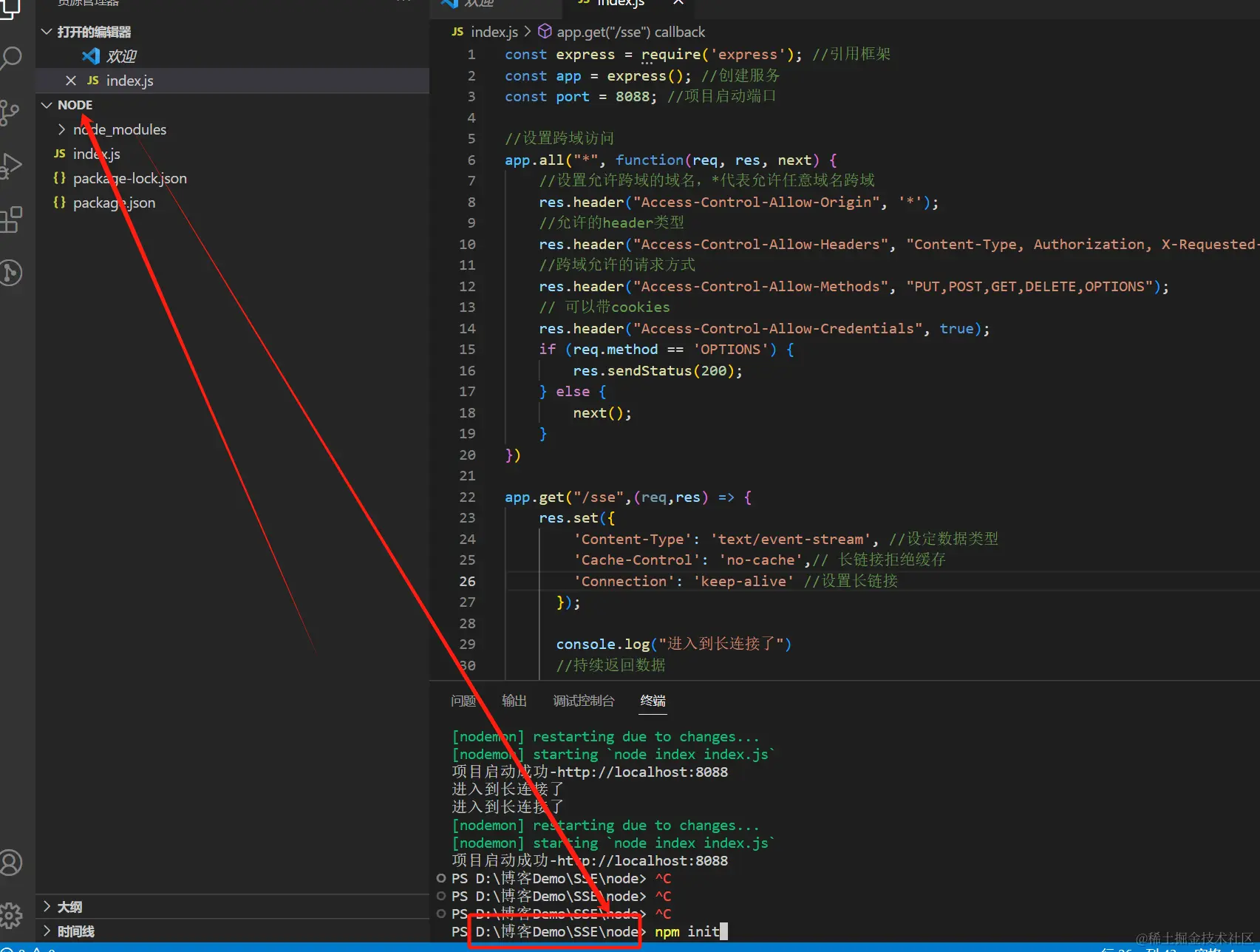
都2024了,你还在使用websocket实现实时消息推送吗?
前言 在日常的开发中,我们经常能碰见服务端需要主动推送给客户端数据的业务场景,比如数据大屏的实时数据,比如消息中心的未读消息,比如聊天功能等等。 本文主要介绍SSE的使用场景和如何使用SSE。 服务端向客户端推送数据的实现…...

javaScript实现客户端直连华为云OBS实现文件上传、断点续传、断网重传
写在前面:在做这个调研时我遇到的需求是前端直接对接华为云平台实现文件上传功能。上传视频文件通常十几个G、客户工作环境网络较差KB/s,且保证上传是稳定的,支持网络异常断点重试、文件断开支持二次拖入自动重传等。综合考虑使用的华为云的分…...
微信小程序:实现微信小程序应用首页开发 (本地生活首页)
文章目录 小程序应用页面开发1、创建项目并配置项目目录结构配置导航栏效果三、配置 tabBar 效果四、轮播图实现4.1 创建轮播图数据容器4.2 定义一个请求轮播图数据的接口4.3 页面加载调用 数据请求接口 五、九宫格实现5.1 获取九宫格数据5.2 结构和样式的完善六、图片布局实现…...

【JavaScript】原型链和继承
文章目录 1. 原型链的概念原型原型链 2. 构建原型链构造函数与原型实例与原型链 3. 继承的实现原型链继承原型链的问题 4. 继承的最佳实践构造函数继承(经典继承)组合继承 5. ES6中的类和继承6. 总结 在 JavaScript 中,原型链和继承是构建对象…...
(二)【Jmeter】专栏实战项目靶场drupal部署
该专栏后续实战示例,都以该篇部署的项目展开操作。 前置条件 参考“(一)【Jmeter】JDK及Jmeter的安装部署及简单配置” 安装部署Jmeter,从文章最后下载“Postman、Rancher.ova、VirtualBox-7.0.12-159484-Win.exe、Xshell-7.0.01…...

使用 ChatGPT系统学习一门知识的技巧
如何使用 ChatGPT 高效学习一门知识?我探索到一种比较高效的方式:首先让 ChatGPT 给你一个学习提纲,然后以此把提纲内容逐个发给 ChatGPT,进行详情学习。 下面以“学习八木天线”工作原理为例说明。 以八木天线为切入点࿰…...
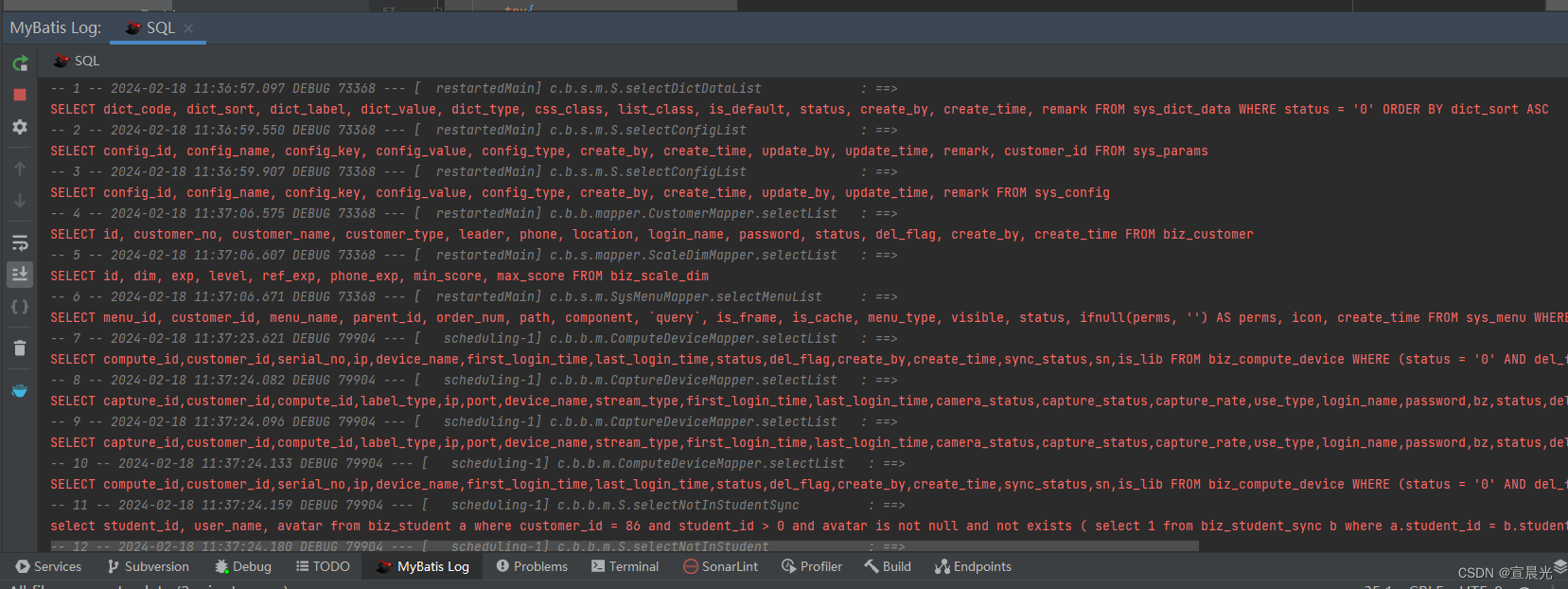
IDEA-常用插件
1、Mybatis Log Free 当我们使用mybatis log在控制台输出sql 内容,输出内容将语句与参数分开打印,还需要手动将参数替换到指定位置。 使用对应插件后,自动将输出内容组装成完整的可直接执行的SQL 在插件市场 查看对应名称,并安装。…...

揭秘:一行代码搞定.Net API高并发的烦恼
高并发下的接口请求重复提交问题 在.Net开发中,我们经常遇到用户疯狂点击同一按钮,或者服务响应慢时重复发送请求,导致数据重复添加或混乱。这不仅浪费资源,更会得到错误的业务结果。如何高效解决这一普遍问题呢? 常规…...

SpringBoot的 8 个优点
目录 1、简化配置 2、快速开发 3、微服务支持 4、内嵌服务器 5、健康监测 6、热部署 7、自动化管理 8、社区支持和生态系统 SpringBoot 是一个基于 Spring 框架的快速开发框架,它通过提供一系列的自动配置、约定优于配置、快速集成等功能,简化了…...

Spark中多分区写文件前可以不排序么
背景 Spark 3.5.0 目前 Spark中的实现中,对于多分区的写入默认会先排序,这是没必要的。可以设置spark.sql.maxConcurrentOutputFileWriters 为大于0来避免排序。 分析 这部分主要分为三个部分: 一个是V1Writes规则的重改; 另一个是FileFormatWriter中…...
)
突破编程_C++_面试(变量与常量)
面试题 1 : C 中的变量存储类别有哪些,并简要描述它们的特点? 在C中,变量的存储类别决定了变量的生命周期和可见性。以下是C中的几种变量存储类别及其特点: 自动存储期 也称为局部存储类别。这类变量在函数或代码块…...
)
k8s的一些关键信息(归类摘抄,非提炼)
零:举例说明 当用户提交一个 Deployment 对象到 Kubernetes 集群时,控制平面的 API Server 接收到该请求,并将其转发给 Controller Manager。Controller Manager 中的 Deployment Controller 监听到该请求,并根据用户定义的配置信…...

海外媒体发稿:8个提升影响力的日韩地区媒体发稿推广策略-华媒舍
在今天的数字化时代,媒体发稿推广成为企业和个人增加影响力的重要方式。特别是在日韩地区,这个拥有庞大媒体市场和活跃社交媒体用户的地区,正确的推广策略将对影响力的提升起到关键作用。我们将介绍8个提升影响力的日韩地区媒体发稿推广策略。…...

面试官:能不能给 Promise 增加取消功能和进度通知功能... 我:???
扯皮 这段时间闲着没事就去翻翻红宝书,已经看到 Promise 篇了,今天又让我翻到两个陌生的知识点。 因为 Promise 业务场景太多了自我感觉掌握的也比较透彻,之前也跟着 Promise A 的规范手写过完整的 Promise,所以这部分内容基本上…...

详解MySQL增删查改
众所周知,MySQL是非常重要的数据库语言,下面我们来回顾一下mysql的增删查改吧 MySQL创建数据库: CREATE DATABASE 数据库名;MySQL删除数据库: DROP DATABASE <database_name>; --直接删除,不检查是否存在 DROP…...

Mysql开启bin-log日志
目录 一、安装配置 二、mysqlbinlog命令 一、安装配置 yum -y install mariadb mariadb-server#安装mysql数据库#默认配置文件/etc/my.cnfvim /etc/my.cnflog-binmariadb-bin #开启二进制日志 systemctl restart mariadb#会在/car/lib/mysql/产生二进制日志文件࿰…...

【网络】每天掌握一个Linux命令 - iftop
在Linux系统中,iftop是网络管理的得力助手,能实时监控网络流量、连接情况等,帮助排查网络异常。接下来从多方面详细介绍它。 目录 【网络】每天掌握一个Linux命令 - iftop工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景…...

突破不可导策略的训练难题:零阶优化与强化学习的深度嵌合
强化学习(Reinforcement Learning, RL)是工业领域智能控制的重要方法。它的基本原理是将最优控制问题建模为马尔可夫决策过程,然后使用强化学习的Actor-Critic机制(中文译作“知行互动”机制),逐步迭代求解…...

VB.net复制Ntag213卡写入UID
本示例使用的发卡器:https://item.taobao.com/item.htm?ftt&id615391857885 一、读取旧Ntag卡的UID和数据 Private Sub Button15_Click(sender As Object, e As EventArgs) Handles Button15.Click轻松读卡技术支持:网站:Dim i, j As IntegerDim cardidhex, …...

工业安全零事故的智能守护者:一体化AI智能安防平台
前言: 通过AI视觉技术,为船厂提供全面的安全监控解决方案,涵盖交通违规检测、起重机轨道安全、非法入侵检测、盗窃防范、安全规范执行监控等多个方面,能够实现对应负责人反馈机制,并最终实现数据的统计报表。提升船厂…...

DockerHub与私有镜像仓库在容器化中的应用与管理
哈喽,大家好,我是左手python! Docker Hub的应用与管理 Docker Hub的基本概念与使用方法 Docker Hub是Docker官方提供的一个公共镜像仓库,用户可以在其中找到各种操作系统、软件和应用的镜像。开发者可以通过Docker Hub轻松获取所…...

centos 7 部署awstats 网站访问检测
一、基础环境准备(两种安装方式都要做) bash # 安装必要依赖 yum install -y httpd perl mod_perl perl-Time-HiRes perl-DateTime systemctl enable httpd # 设置 Apache 开机自启 systemctl start httpd # 启动 Apache二、安装 AWStats࿰…...

生成 Git SSH 证书
🔑 1. 生成 SSH 密钥对 在终端(Windows 使用 Git Bash,Mac/Linux 使用 Terminal)执行命令: ssh-keygen -t rsa -b 4096 -C "your_emailexample.com" 参数说明: -t rsa&#x…...

12.找到字符串中所有字母异位词
🧠 题目解析 题目描述: 给定两个字符串 s 和 p,找出 s 中所有 p 的字母异位词的起始索引。 返回的答案以数组形式表示。 字母异位词定义: 若两个字符串包含的字符种类和出现次数完全相同,顺序无所谓,则互为…...

工业自动化时代的精准装配革新:迁移科技3D视觉系统如何重塑机器人定位装配
AI3D视觉的工业赋能者 迁移科技成立于2017年,作为行业领先的3D工业相机及视觉系统供应商,累计完成数亿元融资。其核心技术覆盖硬件设计、算法优化及软件集成,通过稳定、易用、高回报的AI3D视觉系统,为汽车、新能源、金属制造等行…...

企业如何增强终端安全?
在数字化转型加速的今天,企业的业务运行越来越依赖于终端设备。从员工的笔记本电脑、智能手机,到工厂里的物联网设备、智能传感器,这些终端构成了企业与外部世界连接的 “神经末梢”。然而,随着远程办公的常态化和设备接入的爆炸式…...
