网络工程师学习笔记——IPV6
20世纪80年代,IETF(Internet Engineering Task Force,因特网工程任务组)发布RFC791,即IPv4协议,标志IPv4正式标准化。在此后的几十年间,IPv4协议成为最主流的协议之一。无数人在IPv4的基础上开发出了各种应用,并且对这个协议做了各种补充和增强,支撑起了今天繁荣的互联网。
然而,随着互联网的规模越来越大,以及5G、物联网等新兴技术的发展,IPv4面临的挑战越来越多。IPv6取代IPv4势在必行。
一、为什么需要IPV6?

总而言之,ipv4已经无法满足应用且问题越来越多。相比ipv4,ipv6运用更灵活。
IPv6的优势:

二、IPv6报头
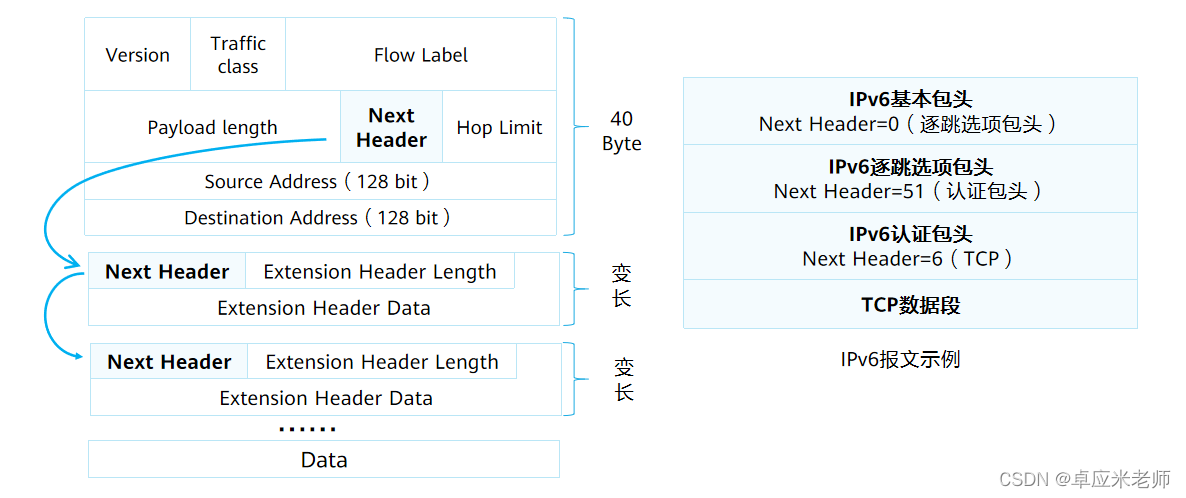
ipv6报头由ipv6基本包头和扩展报头组成。
2.1 ipv6基本报头
version:版本
traffic class:流类别(用于服务质量)
Flow Label:流标签
Payload Length:载荷长度=总长度
Next Header:下一个头部=协议号(识别上层协议)
Hop limit:跳数限制=TTL
Source Address (128bits):源IP
Destination Address (128bits):目的IP
ipv6比ipv4报文少,转发速度快,效率高

ipv6扩展报头:
IPv6扩展报头是跟在IPv6基本报头后面的可选报头,可以有一个或多个,扩展报头是分片扩展报头。
Extension Header Length:扩展包头长度,长度为8 bit。表示扩展包头的长度(不包含Next Header字段)。
Extension Header Data:扩展包头数据,长度可变。扩展包头的内容,为一系列选项字段和填充字段的组合。
| 更多计算机网络相关学习资料领取
|
三、IPv6地址
ipv6是冒分十六进制数表示方式,IPv6地址长度为128比特,每16比特划分为一段,每段由4个十六进制数表示
一个十六进数等于四个比特,一个八组共三十二比特。
ipv6由两部分组成:网络前缀和接口标识。
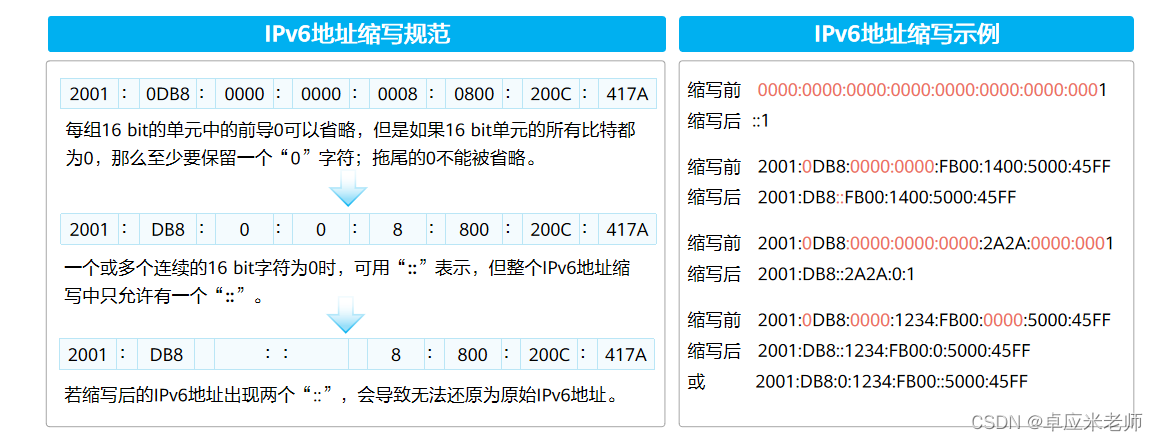
IPv6地址通常写作xxxx:xxxx:xxxx:xxxx:xxxx:xxxx:xxxx:xxxx,每一组中的前导0可以省略,多个0可以用一个0表示,连续全为0的组,可以用双冒号“::”来代替,在一个IPv6地址中只能使用一次双冒号“::”。
 为了书写方便,IPv6可采用以下规则进行缩写。
为了书写方便,IPv6可采用以下规则进行缩写。
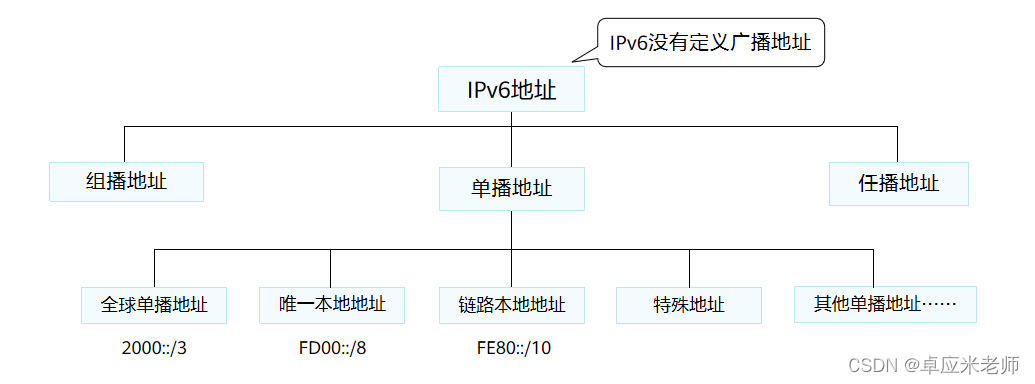
四、ipv6地址分类
根据IPv6地址前缀,可将IPv6地址分为为单播地址、组播地址和任播地址。
4.1 单播
200 0::/3:前三个比特相同
2=0010,前三比特=001的为单播地址

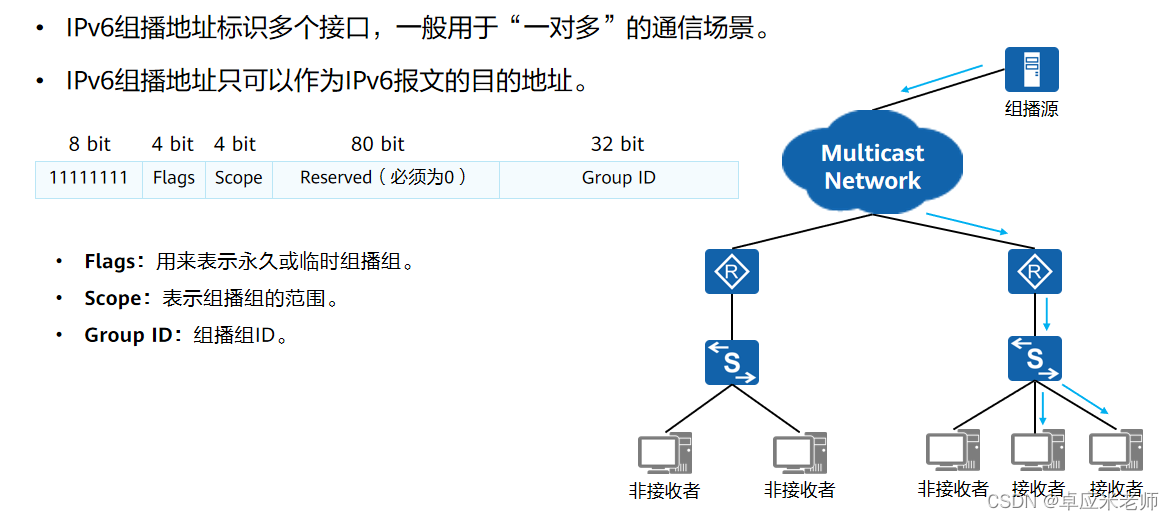
4.2 组播
FF00::/8前8个比特为1
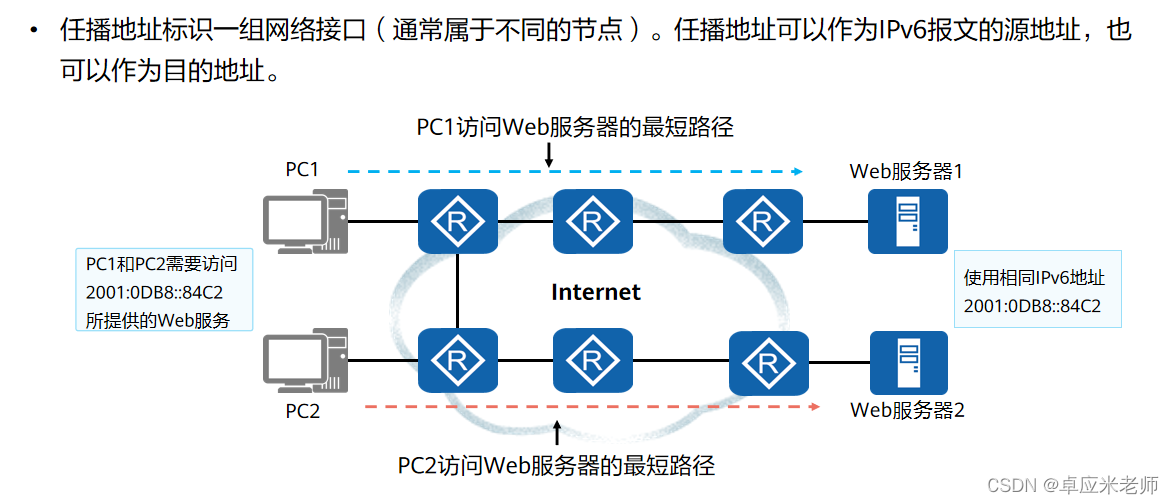
4.3 任播
一到最近
| 更多计算机网络相关学习资料领取
|
| ↓ 关注+点赞后 ↓,文章底部联系我领取 |
相关文章:
网络工程师学习笔记——IPV6
20世纪80年代,IETF(Internet Engineering Task Force,因特网工程任务组)发布RFC791,即IPv4协议,标志IPv4正式标准化。在此后的几十年间,IPv4协议成为最主流的协议之一。无数人在IPv4的基础上开发…...
)
【零基础学习CAPL】——CAN报文的发送(LiveCounter——生命信号)
🙋♂️【零基础学习CAPL】系列💁♂️点击跳转 文章目录 1.概述2.面板创建3.系统变量创建4.CAPL实现5.效果5.1.0~15循环发送5.2.固定值发送6.全量脚本1.概述 本章主要介绍带有生命信号LiveCounter的报文发送脚本 一般报文可使用CANoe的IG模块直接发送,但存在循环冗余…...

git提交代码冲突
用idea2023中的git提交代码,出现 error: Your local changes to the following files would be overwritten by merge: ****/****/****/init.lua Please commit your changes or stash them before you merge. Aborting 出现这个错误可能是因为你的本地修改与远…...

树莓派:使用mdadm为重要数据做RAID 1保护
树莓派作为个人服务器可玩性还是有点的。说到服务器,在企业的生成环境中为了保护数据,基本上都会用到RAID技术。比如,服务器两块小容量但高性能的盘做个RAID-1按装操作系统,余下的大容量中性能磁盘做个RAID-5或者RAID-6存放数据。…...

HTML板块左右排列布局——左侧 DIV 固定宽度,右侧 DIV 自适应宽度,填充满剩余页面
我们可以借助CSS中的 float 属性来实现。 实例: 布局需求: 左侧 DIV 固定宽度,右侧 DIV 自适应宽度,填充满剩余页面。 <!DOCTYPE html> <html><head><meta charset"UTF-8"><meta http-e…...

红旗linux安装32bit依赖库
红旗linux安装32bit依赖库 红旗linux安装32bit依赖库 lib下载 红旗-7.3-lib-32.tar.gz 解压压缩包,根据如下进行操作 1.回退glibc(1)查看当前glibc版本[root192 ~]# rpm -qa | grep glibcglibc-common-2.17-157.axs7.1.x86_64glibc-headers-2.17-260.axs7.5.x86_…...
Stable Diffusion教程——使用TensorRT GPU加速提升Stable Diffusion出图速度
概述 Diffusion 模型在生成图像时最大的瓶颈是速度过慢的问题。为了解决这个问题,Stable Diffusion 采用了多种方式来加速图像生成,使得实时图像生成成为可能。最核心的加速是Stable Diffusion 使用了编码器将图像从原始的 3512512 大小转换为更小的 46…...
NFTScan | 02.12~02.18 NFT 市场热点汇总
欢迎来到由 NFT 基础设施 NFTScan 出品的 NFT 生态热点事件每周汇总。 周期:2024.02.12~ 2024.02.18 NFT Hot News 01/ CryptoPunks 推出「Punk in Residence」孵化器计划 2 月 12 日,NFT 项目 CryptoPunks 宣布推出「Punk in Residence」孵化器计划&a…...
使用 apt 源安装 ROCm 6.0.x 在Ubuntu 22.04.01
从源码编译 rocSolver 本人只操作过单个rocm版本的情景,20240218 ubuntu 22.04.01 1,卸载原先的rocm https://docs.amd.com/en/docs-5.1.3/deploy/linux/os-native/uninstall.html # Uninstall single-version ROCm packages sudo apt autoremove ro…...

python函数的定义和调用
1. 函数的基本概念 在编程中,函数就像是一台机器,接受一些输入(参数),进行一些操作,然后产生输出(结果)。这让我们的代码更加模块化和易于理解。 函数是一段封装了一系列语句的代码…...

【JVM篇】什么是类加载器,有哪些常见的类加载器
文章目录 🍔什么是类加载器🛸有哪些常见的类加载器 🍔什么是类加载器 负责在类加载过程中,将字节码信息以流的方式获取并加载到内存当中 🛸有哪些常见的类加载器 启动类加载器 启动类加载器是有Hotspot虚拟机通过的类…...

STM32—DHT11温湿度传感器
文章目录 一.温湿度原理1.1 时序图 二.代码 一.温湿度原理 1.1 时序图 (1).下图一是DHT11总的时序图。 (2).图二对应图一的左边黑色部分,图三对应图一的绿色部分,图四的左部分图对应图一的红色部分,图四的右部分对应图一的黄色部分。 (3)…...

相机图像质量研究(31)常见问题总结:图像处理对成像的影响--图像差
系列文章目录 相机图像质量研究(1)Camera成像流程介绍 相机图像质量研究(2)ISP专用平台调优介绍 相机图像质量研究(3)图像质量测试介绍 相机图像质量研究(4)常见问题总结:光学结构对成像的影响--焦距 相机图像质量研究(5)常见问题总结:光学结构对成…...
MySQL之select查询
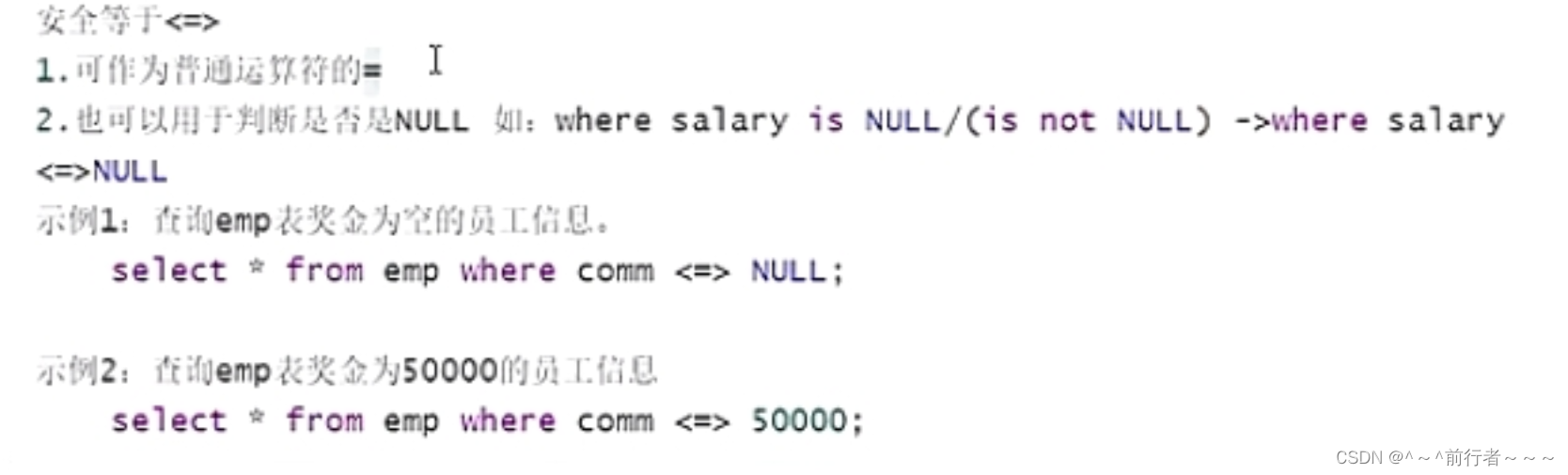
华子目录 SQL简介SQL语句分类SQL语句的书写规范SQL注释单行注释多行注释 select语句简单的select语句select的算数运算select 要查询的信息 from 表名;查询表字段查询常量查询表达式查询函数 查询定义别名as安全等于<>去重distinct连接字段concat 模糊查询运算符比较运算…...
Android MMKV 接入+ 替换原生 SP + 原生 SP 数据迁移
背景:项目中一直使用的是原生 SP,众所周知,使用原生 SP 存在卡顿性能问题。公司的性能监控平台抓到不少原生 SP 导致的 ANR 问题: java.io.FileDescriptor.sync (FileDescriptor.java) android.os.FileUtils.sync (FileUtils.java:256) android.app.SharedPreferencesImpl.…...

C#上位机与三菱PLC的通信07--使用第3方通讯库读写数据
1、通讯库介绍 mcprotocol 是一个基于 Node.js 的三菱 PLC MC 协议通信库,具有以下特点: 支持多种三菱 PLC MC 协议的设备,如 FX3U、Q03UDECPU、QJ71E71 等。 支持多种功能码和数据类型,如读取线圈(M)、…...
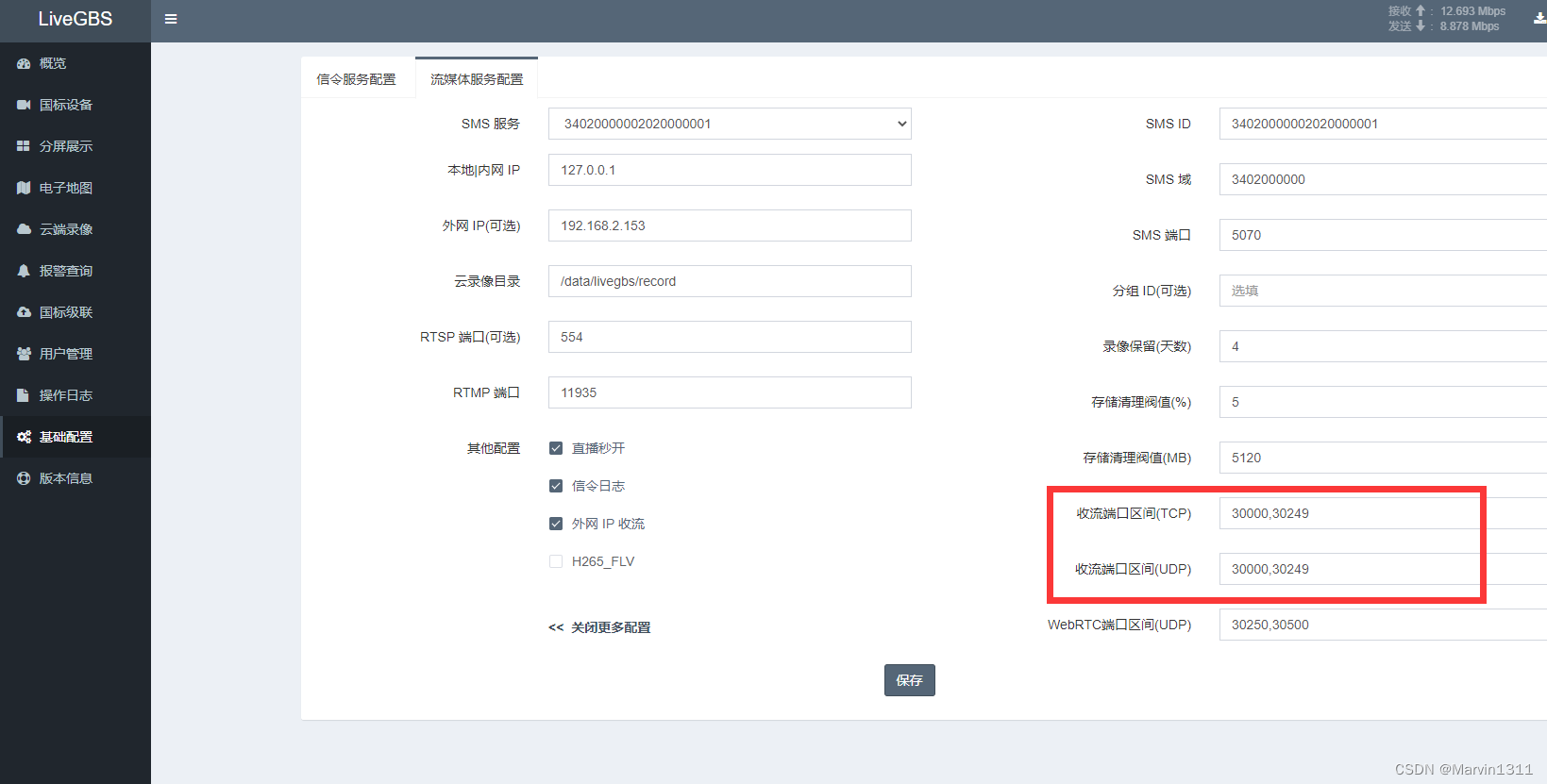
LiveGBS流媒体平台GB/T28181常见问题-基础配置流媒体服务配置中本地|内网IP外网IP(可选)外网IP收流如何配置
LiveGBS常见问题基础配置流媒体服务配置中本地|内网IP外网IP外网IP收流如何配置? 1、流媒体服务配置2、播放提示none rtp data receive3、多网卡服务器4、收流端口配置5、端口区间可以如何配置6、搭建GB28181视频直播平台 1、流媒体服务配置 LiveGBS中基础配置-》流…...

微服务- 熔断、降级和限流
基本介绍 在微服务架构中,由于服务之间的相互依赖性,任何一个服务的故障或性能问题都可能导致整个系统的不稳定。因此,熔断、降级和限流是三种常见的技术手段,用于提高系统的可用性和稳定性。 熔断 (Circuit Breaker) 熔断机制…...
电路设计(20)——数字电子钟的multism仿真
1.设计要求 使用数字芯片,设计一个电子钟,用数码管显示,可以显示星期,时、分、秒,可以有按键校准时间。有整点报警功能。 2.设计电路 设计好的multism电路图如下所示 3.芯片介绍 时基脉冲使用555芯片产生。在仿真里面…...

【论文阅读笔记】Contrastive Learning with Stronger Augmentations
Contrastive Learning with Stronger Augmentations 摘要 基于提供的摘要,该论文的核心焦点是在对比学习领域提出的一个新框架——利用强数据增强的对比学习(Contrastive Learning with Stronger Augmentations,简称CLSA)。以下…...

vscode里如何用git
打开vs终端执行如下: 1 初始化 Git 仓库(如果尚未初始化) git init 2 添加文件到 Git 仓库 git add . 3 使用 git commit 命令来提交你的更改。确保在提交时加上一个有用的消息。 git commit -m "备注信息" 4 …...

STM32+rt-thread判断是否联网
一、根据NETDEV_FLAG_INTERNET_UP位判断 static bool is_conncected(void) {struct netdev *dev RT_NULL;dev netdev_get_first_by_flags(NETDEV_FLAG_INTERNET_UP);if (dev RT_NULL){printf("wait netdev internet up...");return false;}else{printf("loc…...

STM32标准库-DMA直接存储器存取
文章目录 一、DMA1.1简介1.2存储器映像1.3DMA框图1.4DMA基本结构1.5DMA请求1.6数据宽度与对齐1.7数据转运DMA1.8ADC扫描模式DMA 二、数据转运DMA2.1接线图2.2代码2.3相关API 一、DMA 1.1简介 DMA(Direct Memory Access)直接存储器存取 DMA可以提供外设…...

微信小程序 - 手机震动
一、界面 <button type"primary" bindtap"shortVibrate">短震动</button> <button type"primary" bindtap"longVibrate">长震动</button> 二、js逻辑代码 注:文档 https://developers.weixin.qq…...

Qwen3-Embedding-0.6B深度解析:多语言语义检索的轻量级利器
第一章 引言:语义表示的新时代挑战与Qwen3的破局之路 1.1 文本嵌入的核心价值与技术演进 在人工智能领域,文本嵌入技术如同连接自然语言与机器理解的“神经突触”——它将人类语言转化为计算机可计算的语义向量,支撑着搜索引擎、推荐系统、…...

linux 下常用变更-8
1、删除普通用户 查询用户初始UID和GIDls -l /home/ ###家目录中查看UID cat /etc/group ###此文件查看GID删除用户1.编辑文件 /etc/passwd 找到对应的行,YW343:x:0:0::/home/YW343:/bin/bash 2.将标红的位置修改为用户对应初始UID和GID: YW3…...

高防服务器能够抵御哪些网络攻击呢?
高防服务器作为一种有着高度防御能力的服务器,可以帮助网站应对分布式拒绝服务攻击,有效识别和清理一些恶意的网络流量,为用户提供安全且稳定的网络环境,那么,高防服务器一般都可以抵御哪些网络攻击呢?下面…...

【论文阅读28】-CNN-BiLSTM-Attention-(2024)
本文把滑坡位移序列拆开、筛优质因子,再用 CNN-BiLSTM-Attention 来动态预测每个子序列,最后重构出总位移,预测效果超越传统模型。 文章目录 1 引言2 方法2.1 位移时间序列加性模型2.2 变分模态分解 (VMD) 具体步骤2.3.1 样本熵(S…...

A2A JS SDK 完整教程:快速入门指南
目录 什么是 A2A JS SDK?A2A JS 安装与设置A2A JS 核心概念创建你的第一个 A2A JS 代理A2A JS 服务端开发A2A JS 客户端使用A2A JS 高级特性A2A JS 最佳实践A2A JS 故障排除 什么是 A2A JS SDK? A2A JS SDK 是一个专为 JavaScript/TypeScript 开发者设计的强大库ÿ…...

在Mathematica中实现Newton-Raphson迭代的收敛时间算法(一般三次多项式)
考察一般的三次多项式,以r为参数: p[z_, r_] : z^3 (r - 1) z - r; roots[r_] : z /. Solve[p[z, r] 0, z]; 此多项式的根为: 尽管看起来这个多项式是特殊的,其实一般的三次多项式都是可以通过线性变换化为这个形式…...