趣学贝叶斯统计:概率密度分布(probability density function)
目录
- 1. 分布:PDF与PMF
- PMF
- 2. 将概率密度函数应用于我们的问题
- 用积分量化连续分布
- 积分
- 度量变化率:导数
- 3. R语言实践
- 4. 小结
1. 分布:PDF与PMF
PDF定义在连续值上。在连续型随机变量的情况下,具体取某个数值的概率是0,因此PDF并不直接给出某个点的概率,而是给出了在某个区间内随机变量出现的概率密度。在数学上,PDF就是定义在连续值上的概率密度函数。
概率密度函数(probability density function,PDF): β \beta β 分布
B e t a ( p ; a , b ) = p a − 1 ⋅ ( 1 − p ) b − 1 B ( a , b ) Beta(p;a,b) = \frac{p^{a-1} \cdot (1-p)^{b-1}}{B(a, b)} Beta(p;a,b)=B(a,b)pa−1⋅(1−p)b−1
其中, 0 ≤ x ≤ 1 0\leq x \leq 1 0≤x≤1, a > b > 0 a \gt b \gt 0 a>b>0。
p: 事件概率。黑盒子吐出两枚硬币可能概率的不同假设。
a:观察到的时间次数。黑盒子吐出两枚硬币。
b:事件不发生的次数。黑盒子吞掉硬币的次数。
实验总次数:a+b。
PMF
PMF实验总次数是n, k是感兴趣的发生次数。
注意:分子不一样。
f ( k ∣ n , p ) = ( n k ) p k ( 1 − p ) n − k f(k|n,p) = \binom{n}{k} p^k (1-p)^{n-k} f(k∣n,p)=(kn)pk(1−p)n−k
PMF分子是 p k ( 1 − p ) n − k p^k (1-p)^{n-k} pk(1−p)n−k
PDF分子是 p a − 1 ⋅ ( 1 − p ) b − 1 p^{a-1} \cdot (1-p)^{b-1} pa−1⋅(1−p)b−1,指数项需要分别减1。我们从指数项中减去1,并使用beta函数归一化所得的值——这可以确保分布之和为1。
我们最后得到了这样一个函数:它描述的是每个可能假设的概率,这些假设是我们相信从盒子里得到两枚硬币的概率,前提是给定我们已经观察到一种结果出现a次、另一种结果出现b次。
β \beta β 分布代表了所有可能的二项分布对观察结果的最高描述程度。
2. 将概率密度函数应用于我们的问题
a=14; b=27

import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import beta# 定义参数
a = 14
b = 27# 生成 x 值的范围
x = np.linspace(0, 1, 1000)# 计算 Beta 分布的概率密度函数(PDF)
pdf = beta.pdf(x, a, b)# 绘制图形
plt.plot(x, pdf, 'r-', lw=2, label='PDF of Beta Distribution')
plt.title('Probability Density Function (PDF) of Beta Distribution (a=14, b=27)')
plt.xlabel('x')
plt.ylabel('Probability Density')
plt.legend()
plt.grid(True)
plt.show()通过这个黑盒子赔钱的概率要比赢钱的概率大。虽然通过图5-3可以看出信念的分布,但我们还是希望能够准确地量化自己相信“黑盒子返回两枚硬币的概率小于0.5”的程度。要做到这一点,我们只需要懂一点微积分(和R语言)。
用积分量化连续分布
计算曲线下面积:积分
作者之前是不熟悉积分的,所以我们会从最基本的概念开始理解。依旧a=14; b=27, 我们想知道:吐出两枚硬币的可能性是 1 2 \frac {1}{2} 21 的概率是多少?
我们知道概率的基本规则是,所有概率的和必然等于1。但在连续分布里,每个单独的值都无穷小,这就意味着任何特定值的概率实际上都是0。
二项分布:想象一下,你把一块1千克重的巧克力(相当大!)平均分成了两份,那么每份就有 1 2 \frac {1}{2} 21 千克重。
连续分布:如果你把它平均分成了10份,那么每份将重 1 10 \frac {1}{10} 101千克。随着你将巧克力分成的份数越来越多,每一份就会变得越来越小,小到你甚至看不见它。当分成的份数无穷大时,每一份就会小得看不见,就好像消失了!
即使单独的每一份都消失了,我们仍然可以讨论一定范围内的情况。例如,即使将一块1千克重的巧克力分成了无限多块,我们仍然可以将其中一半块数的重量加起来。同样,当讨论连续分布中的概率时,我们也可以将某个范围内的值相加。但如果每个具体的值都接近于0,那么它们的和是不是仍然等于0呢?
积分
这就是微积分要解决的问题。在微积分中,有一种求无穷小值和的特殊方法,叫作积分(integral)。如果想知道黑盒子返回硬币的概率是否小于0.5(也就是值在0和0.5之间),那么我们可以这样求和:
∫ 0 0.5 f ( x ) d x \int_{0}^{0.5} f(x) \, dx ∫00.5f(x)dx
这里的∫只是一个拉伸后的S,意思是f(x)中所有矩形的面积之和。dx符号则提醒我们所谈论的是变量x很小的变化;d是表示这些矩形的一种数学方法。当然,在这个符号中只有一个变量x,所以我们不会混淆。而且,在本书中通常会删除dx(或变量中所使用的相应值),因为即使在示例中不写,我们也可以明白。
d i s t ( T ) = ∫ 0 T f ( t ) d t dist(T)= \int_{0}^{T} f(t) \, dt dist(T)=∫0Tf(t)dt
积分可以帮助我们把“某一时间的速度”,转化为函数即“某一段时间的跑步距离”。
度量变化率:导数
这里使用了类似于前面解释积分的方法:积分时把曲线下的区域分成越来越细的矩形,直到包含无数个细矩形,然后将它们的面积相加;只不过这里是把曲线分成无数个小线段。最终,我们得到了一个新的函数而不是单一的斜率m,来表示原始函数中每个点的变化率。这被称为导数(derivative).
d d x F ( x ) = f ( x ) \frac{d}{dx}F(x)=f(x) dxdF(x)=f(x)
F为f的原函数。
现在假设对函数f,我们想在10和50之间对其积分,也就是要计算:
∫ 10 50 f ( x ) d x = F ( 50 ) − F ( 10 ) \int_{10}^{50} f(x) \, dx=F(50)-F(10) ∫1050f(x)dx=F(50)−F(10)
积分和导数之间的关系被称为微积分基本定理(fundamental theorem of calculus)。这是一个相当神奇的工具,因为它允许用数学方法来解决积分问题,这往往要比求导数困难得多。
3. R语言实践
R语言中有一个名为dbeta()的函数,它就是beta分布的PDF。将它和integrate()函数一起使用就可以自动计算积分。
计算0-0.5之间的概率密度:
> integrate(function(p) dbeta(p,14,27),0,0.5)
结果:
0.9807613 with absolute error < 5.9e-06
之所以出现绝对误差(absolute error),是因为计算机不能完美地计算积分,而总会有一些误差。不过通常情况下误差很小,我们不用担心。R语言计算出的这个结果告诉我们,根据目前观察到的数据,从黑盒子中得到两枚硬币的真实概率小于0.5的概率高达0.98。这意味着往黑盒子里放更多的硬币不是好主意,因为你很有可能会输钱。
我们可以用收集到的数据去计算抽牌/抽奖时,是否应该去碰运气。
4. 小结
在本章中,我们学习了Beta分布,它与二项分布密切相关,其起作用的方式却大不相同。我们通过观察大量可能的二项分布对数据的解释程度建立了Beta分布。由于假设的数量无穷多,因此我们需要一个连续的概率分布来描述所有的假设。Beta分布让我们能够表示自己对所有可能结果的出现概率有多大信心。这使得我们能够对观察到的数据进行统计推理,其方式是通过确定将哪些概率分配给一个事件以及确定自己相信每个概率的程度,这就是表示概率范围的概率。
Beta分布与二项分布的主要区别在于,Beta分布是一个连续的概率分布。由于在分布中有无限多的值,因此我们不能像在离散概率分布中那样对结果进行求和,而是需要使用微积分对一定范围内的数值进行求和。幸运的是,我们可以使用R语言代替手动求解复杂的积分。
相关文章:

趣学贝叶斯统计:概率密度分布(probability density function)
目录 1. 分布:PDF与PMFPDFPMF 2. 将概率密度函数应用于我们的问题用积分量化连续分布积分度量变化率:导数 3. R语言实践4. 小结 1. 分布:PDF与PMF PDF PDF定义在连续值上。在连续型随机变量的情况下,具体取某个数值的概率是0,因此PDF并不直…...

伦敦金行情分析需要学习吗?
对于伦敦金交易来说,目前大致分成两派,一派是实干派,认为做伦敦金交易重要的是实战,不需要学习太多东西,否则容易被理论知识所局限。另一派则是强调学习,没有理论知识,投资者很难做好伦敦金交易…...

Java实现停车场收费系统 JAVA+Vue+SpringBoot+MySQL
目录 一、摘要1.1 项目介绍1.2 项目录屏 二、功能模块2.1 停车位模块2.2 车辆模块2.3 停车收费模块2.4 IC卡模块2.5 IC卡挂失模块 三、系统设计3.1 用例设计3.2 数据库设计3.2.1 停车场表3.2.2 车辆表3.2.3 停车收费表3.2.4 IC 卡表3.2.5 IC 卡挂失表 四、系统实现五、核心代码…...
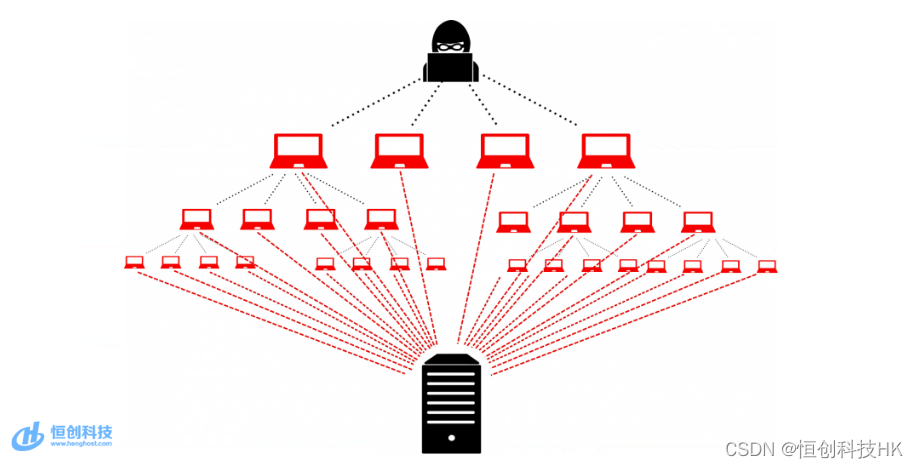
服务器遭受 DDoS 攻击的常见迹象有哪些?
服务器遭受 DDoS 攻击的现象很常见,并且有时不容易预防,有部分原因是它们的形式多种多样,而且黑客手段越来越隐蔽。如果您怀疑自己可能遭受 DDoS 攻击,可以寻找多种迹象。以下是 DDoS 攻击的5个常见迹象: 1.网络流量无…...

【机器学习笔记】 15 机器学习项目流程
机器学习的一般步骤 数据清洗 数据清洗是指发现并纠正数据文件中可识别的错误的最后一道程序,包括检查数据一致性,处理无效值和缺失值等。与问卷审核不同,录入后的数据清理一般是由计算机而不是人工完成。 探索性数据分析(EDA 探索性数据…...
【C语言】位操作符与移位操作符练习
目录 前言: 1.一道变态的面试题 2.输入一个整数 n ,输出该数32位二进制表示中1的个数。其中负数用补码表示。 方法一: 方法二: 方法三: 3.打印整数二进制的奇数位和偶数位 前言: 前篇我们学习过C语言…...

第十四届“中关村青联杯”全国研究生数学建模竞赛-A题:无人机在抢险救灾中的优化运用
目录 摘 要: 1 问题重述 1.1 问题背景 1.2 待解决的问题 2 模型假设及符号说明...

Android 9.0 Launcher3桌面显示多个相同app图标的解决办法
1.前言 在9.0的系统ROM定制化开发中,在Launcher3的系统原生桌面中,在显示桌面的时候,在禁用和启用app的功能测试的时候,会发现有多个相同app的图标显示在桌面 这对Launcher3的体验效果不是很好,所以为了优化产品,需要解决这个bug,然后让产品更完善 2.桌面显示多个相同…...
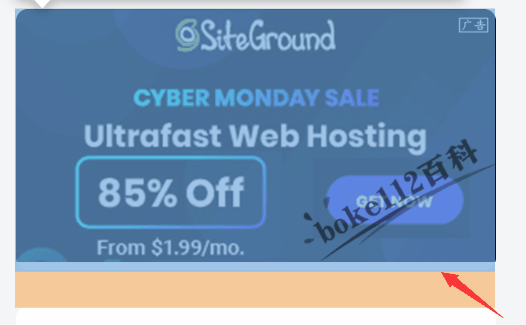
WordPress主题YIA在广告位添加图片广告时下方有空白怎么办?
YIA主题设置中默认有4个广告位,而侧边栏的广告位由站长自行添加。boke112百科在这些广告位添加图片广告后发现图片下方有空白,导致下方的两个角没有变圆角,看起来也有点不好看。具体如下图所示: 其实,这个问题就是典型…...

5.15 BCC工具之kvm_hypercall.py解读
一,工具简介 在该示例中,我们可以了解到如何使用eBPF(扩展BPF,Berkeley Packet Filter的扩展)和bcc(BPF Compiler Collection)来分析KVM(Kernel-based Virtual Machine)中的超级调用(hypercall)。 即当exit_reason为VMCALL时,有状态的kvm_entry和kvm_exit记录以及…...

git 解除本地分支与其它分支(远程分支)的关联
开发中,我在同事的分支开一条分支,并将同事的分支作为关联分支,前两天还好,我一个人在干活,然而第3天,同事回来了,他在他那条分支也开发,这时就会出现2种情况, 1. 同时修…...

conda 所有的命令及其讲解
Conda 是一个开源的包管理器和环境管理器,可以用于安装、运行和升级跨平台的软件包和环境。Conda 很流行于数据科学、机器学习、科学计算等领域,因为它能够快速地安装、管理和部署软件包和环境。以下是 Conda 的一些主要命令及其简要说明: 环…...

mysql 数据库主从复制搭建
MySQL 主从复制主要用于实现高可用性和备份。在主从复制中,一个 MySQL 实例(称为主节点)将其数据更改复制到至少一个其他 MySQL 实例(称为从节点)上。主要借助于数据库二进制日志binlog进行数据的复制。 主从数据库对应…...

小白水平理解面试经典题目LeetCode 1025 Divisor Game【动态规划】
1025 除数游戏 小艾 和 小鲍 轮流玩游戏,小艾首先开始。 最初,黑板上有一个数字 n 。在每个玩家的回合中,该玩家做出的动作包括: 选择任意 x,使 0 < x < n 和 n % x 0 。将黑板上的数字 n 替换为 n - x 。 此…...

基于单片机的智能宠物喂食器设计
摘要:阐述智能宠物喂食器的实现方式,以STC89C52单片机为核心芯片,控制LCD的显示、语音芯片的启动和步进电机的运行。通过按键设置预设时间,当时间到达预设时间时,语音电路发出提示,步进电机工作,提供食物。此系统解决了主人由于各种原因不在家,使得宠物不能按时吃饭的问…...

探索单片机应用领域:从智能家居到工业自动化
单片机作为一种微型计算机芯片,在智能家居和工业自动化领域有着广泛的应用。以下将从智能家居和工业自动化两个方面分点论述单片机的应用。 智能家居领域: 1. 智能灯光控制: 单片机可以用于控制智能灯光系统,实现灯光的远程控制…...

Nginx介绍和使用
Nginx是一个高性能的HTTP和反向代理web服务器,其使用方法包括安装、配置以及与其他软件的配合使用。 Nginx被广泛认为是一个轻量级、占用资源少、并发处理能力强大的web服务器软件。它不仅可以作为HTTP服务器提供静态内容服务,还可以作为反向代理服务器…...

异步编程——CompletableFuture用法详解
文章目录 前言1. Future 线程池2. 什么是CompletableFuture 前言 我们异步执行一个任务时,需要用线程池Executor去创建,有两种方式: 如果不需要有返回值, 任务继承Thread类或实现Runnable接口;如果需要有返回值&…...
)
Linux常用命令(不断更新)
cd 切换目录 cd .. 返回上一级目录 cd ../.. 返回上两级目录 pwd 显示工作路径 ls -l 显示文件和目录的详细信息 ls -a 列出全部文件 ls -R 连同子目录的内容一起列出 ls -lh 显示权限 cp 复制 mv 移动 rm 删除 cat 查看文件内容 find 文件搜索 文件权限 …...
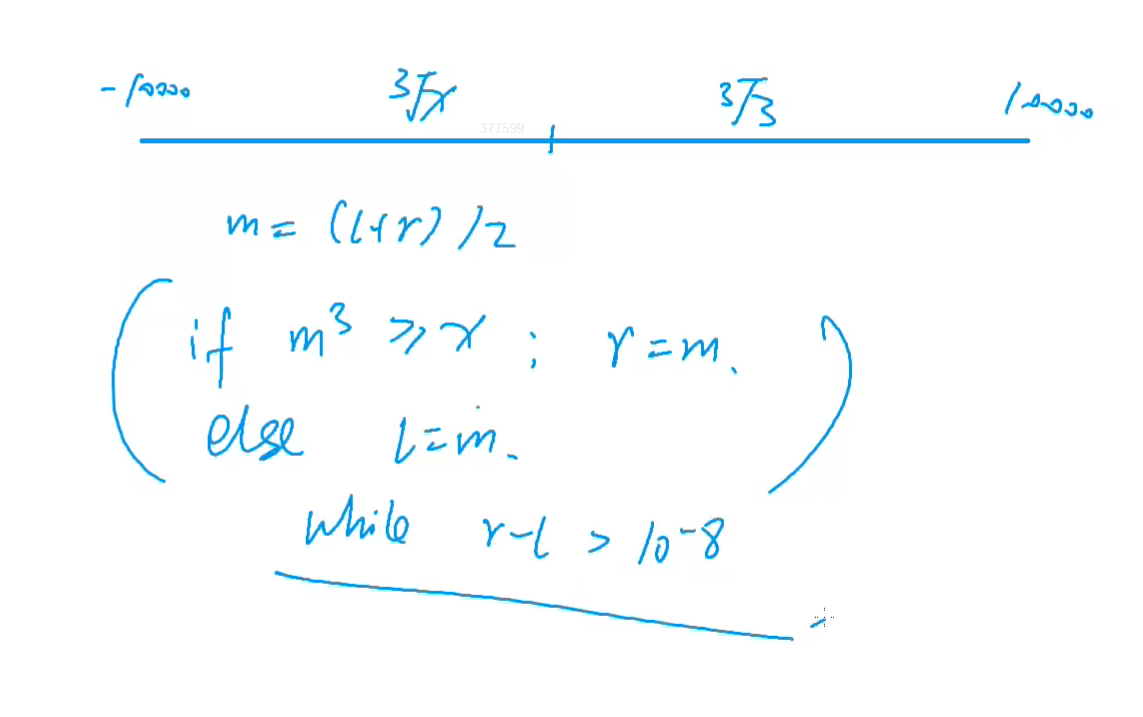
C++ 浮点数二分 数的三次方根
给定一个浮点数 n ,求它的三次方根。 输入格式 共一行,包含一个浮点数 n 。 输出格式 共一行,包含一个浮点数,表示问题的解。 注意,结果保留 6 位小数。 数据范围 −10000≤n≤10000 输入样例: 1000.00…...

Vim 调用外部命令学习笔记
Vim 外部命令集成完全指南 文章目录 Vim 外部命令集成完全指南核心概念理解命令语法解析语法对比 常用外部命令详解文本排序与去重文本筛选与搜索高级 grep 搜索技巧文本替换与编辑字符处理高级文本处理编程语言处理其他实用命令 范围操作示例指定行范围处理复合命令示例 实用技…...

未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?
编辑:陈萍萍的公主一点人工一点智能 未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?RWM通过双自回归机制有效解决了复合误差、部分可观测性和随机动力学等关键挑战,在不依赖领域特定归纳偏见的条件下实现了卓越的预测准…...

Java如何权衡是使用无序的数组还是有序的数组
在 Java 中,选择有序数组还是无序数组取决于具体场景的性能需求与操作特点。以下是关键权衡因素及决策指南: ⚖️ 核心权衡维度 维度有序数组无序数组查询性能二分查找 O(log n) ✅线性扫描 O(n) ❌插入/删除需移位维护顺序 O(n) ❌直接操作尾部 O(1) ✅内存开销与无序数组相…...

【大模型RAG】Docker 一键部署 Milvus 完整攻略
本文概要 Milvus 2.5 Stand-alone 版可通过 Docker 在几分钟内完成安装;只需暴露 19530(gRPC)与 9091(HTTP/WebUI)两个端口,即可让本地电脑通过 PyMilvus 或浏览器访问远程 Linux 服务器上的 Milvus。下面…...

江苏艾立泰跨国资源接力:废料变黄金的绿色供应链革命
在华东塑料包装行业面临限塑令深度调整的背景下,江苏艾立泰以一场跨国资源接力的创新实践,重新定义了绿色供应链的边界。 跨国回收网络:废料变黄金的全球棋局 艾立泰在欧洲、东南亚建立再生塑料回收点,将海外废弃包装箱通过标准…...

WordPress插件:AI多语言写作与智能配图、免费AI模型、SEO文章生成
厌倦手动写WordPress文章?AI自动生成,效率提升10倍! 支持多语言、自动配图、定时发布,让内容创作更轻松! AI内容生成 → 不想每天写文章?AI一键生成高质量内容!多语言支持 → 跨境电商必备&am…...

Go 语言并发编程基础:无缓冲与有缓冲通道
在上一章节中,我们了解了 Channel 的基本用法。本章将重点分析 Go 中通道的两种类型 —— 无缓冲通道与有缓冲通道,它们在并发编程中各具特点和应用场景。 一、通道的基本分类 类型定义形式特点无缓冲通道make(chan T)发送和接收都必须准备好࿰…...

MySQL 知识小结(一)
一、my.cnf配置详解 我们知道安装MySQL有两种方式来安装咱们的MySQL数据库,分别是二进制安装编译数据库或者使用三方yum来进行安装,第三方yum的安装相对于二进制压缩包的安装更快捷,但是文件存放起来数据比较冗余,用二进制能够更好管理咱们M…...

vulnyx Blogger writeup
信息收集 arp-scan nmap 获取userFlag 上web看看 一个默认的页面,gobuster扫一下目录 可以看到扫出的目录中得到了一个有价值的目录/wordpress,说明目标所使用的cms是wordpress,访问http://192.168.43.213/wordpress/然后查看源码能看到 这…...

腾讯云V3签名
想要接入腾讯云的Api,必然先按其文档计算出所要求的签名。 之前也调用过腾讯云的接口,但总是卡在签名这一步,最后放弃选择SDK,这次终于自己代码实现。 可能腾讯云翻新了接口文档,现在阅读起来,清晰了很多&…...
