830. 单调栈
Problem: 830. 单调栈
文章目录
- 思路
- 解题方法
- 复杂度
- Code
思路
这是一个单调栈的问题。单调栈是一种特殊的栈结构,它的特点是栈中的元素保持单调性。在这个问题中,我们需要找到每个元素左边第一个比它小的元素,这就需要使用到单调递增栈。
我们从左到右遍历数组,对于每个元素,如果栈为空或者当前元素大于栈顶元素,就将当前元素入栈;否则,就将栈顶元素出栈,直到栈为空或者找到一个栈顶元素小于当前元素,然后将当前元素入栈。这样,栈中的元素就始终保持了单调递增的性质。
在这个过程中,每当我们要将一个元素出栈时,就找到了这个元素左边第一个比它小的元素(就是当前的栈顶元素)。我们可以在这个时候记录下这个信息。
解题方法
我们使用一个栈和一个二维数组。栈用来存储元素的索引,二维数组用来存储每个元素左边第一个比它小的元素的索引和右边第一个比它小的元素的索引。
在遍历数组的过程中,我们使用一个指针r来表示栈顶。每当我们要将一个元素i入栈时,如果栈不为空并且栈顶元素大于等于当前元素,就将栈顶元素出栈,并记录下这个元素左边第一个比它小的元素的索引(就是当前的栈顶元素)和右边第一个比它小的元素的索引(就是当前的元素i)。然后将元素i入栈。
在遍历完数组后,栈中可能还有元素。这些元素右边没有比它小的元素,所以我们将这些元素出栈,并记录下这个元素左边第一个比它小的元素的索引(就是当前的栈顶元素)。
最后,我们需要修正一下结果。因为可能存在连续的相同的元素,这些元素右边第一个比它小的元素应该是相同的。所以我们从右到左遍历数组,如果一个元素和它右边的元素相同,就将它的右边第一个比它小的元素的索引更新为它右边的元素的右边第一个比它小的元素的索引。
复杂度
时间复杂度:
O ( n ) O(n) O(n),我们只遍历了一次数组。
空间复杂度:
O ( n ) O(n) O(n),我们使用了一个栈和一个二维数组来存储信息。
Code
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.io.OutputStreamWriter;
import java.io.PrintWriter;
import java.io.StreamTokenizer;public class Main {static BufferedReader in = new BufferedReader(new InputStreamReader(System.in));static PrintWriter out = new PrintWriter(new OutputStreamWriter(System.out));static StreamTokenizer sr = new StreamTokenizer(in);static int MAXN = (int) (1e5 + 10);static int n, r;static int[] arr = new int[MAXN];static int[][] ans = new int[MAXN][2];static int[] stack = new int[MAXN];public static void main(String[] args) throws IOException {n = nextInt();for (int i = 0; i < n; i++) {arr[i] = nextInt();}// 找出左边第一个比自己小的元素deal();for (int i = 0; i < n; i++) {if (ans[i][0] != -1) {out.print(arr[ans[i][0]] + " ");} else {out.print(-1 + " ");}}out.flush();}private static void deal() {// TODO Auto-generated method stubint cur;r = 0;// 计算阶段for (int i = 0; i < n; i++) {while (r > 0 && arr[stack[r - 1]] >= arr[i]) {cur = stack[--r];ans[cur][0] = r > 0 ? stack[r - 1] : -1;ans[cur][1] = i;}stack[r++] = i;}// 清算阶段while (r > 0) {cur = stack[--r];ans[cur][0] = r > 0 ? stack[r - 1] : -1;ans[cur][1] = -1;}// 修正阶段for (int i = n - 2; i >= 0; i--) {if (ans[i][1] != -1 && arr[ans[i][1]] == arr[i]) {ans[i][1] = ans[ans[i][1]][1];}}}static int nextInt() throws IOException {sr.nextToken();return (int) sr.nval;}}相关文章:

830. 单调栈
Problem: 830. 单调栈 文章目录 思路解题方法复杂度Code 思路 这是一个单调栈的问题。单调栈是一种特殊的栈结构,它的特点是栈中的元素保持单调性。在这个问题中,我们需要找到每个元素左边第一个比它小的元素,这就需要使用到单调递增栈。 我们…...

H5 个人引导页官网型源码
H5 个人引导页官网型源码 源码介绍:源码无后台、无数据库,H5自检测适应、无加密,直接修改可用。 源码含有多选项,多功能。可展示自己站点、团队站点。手机电脑双端。 下载地址: https://www.changyouzuhao.cn/1434.…...
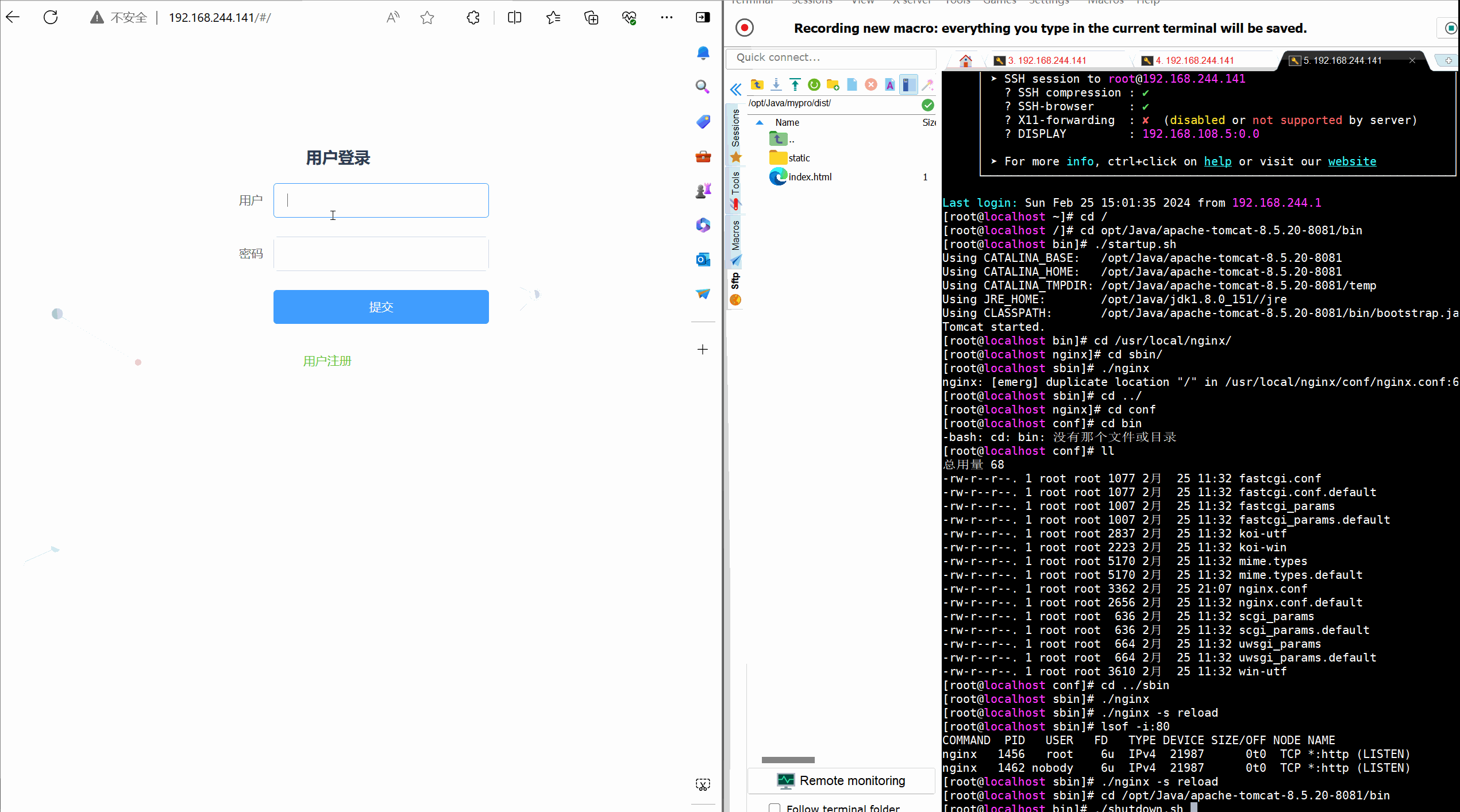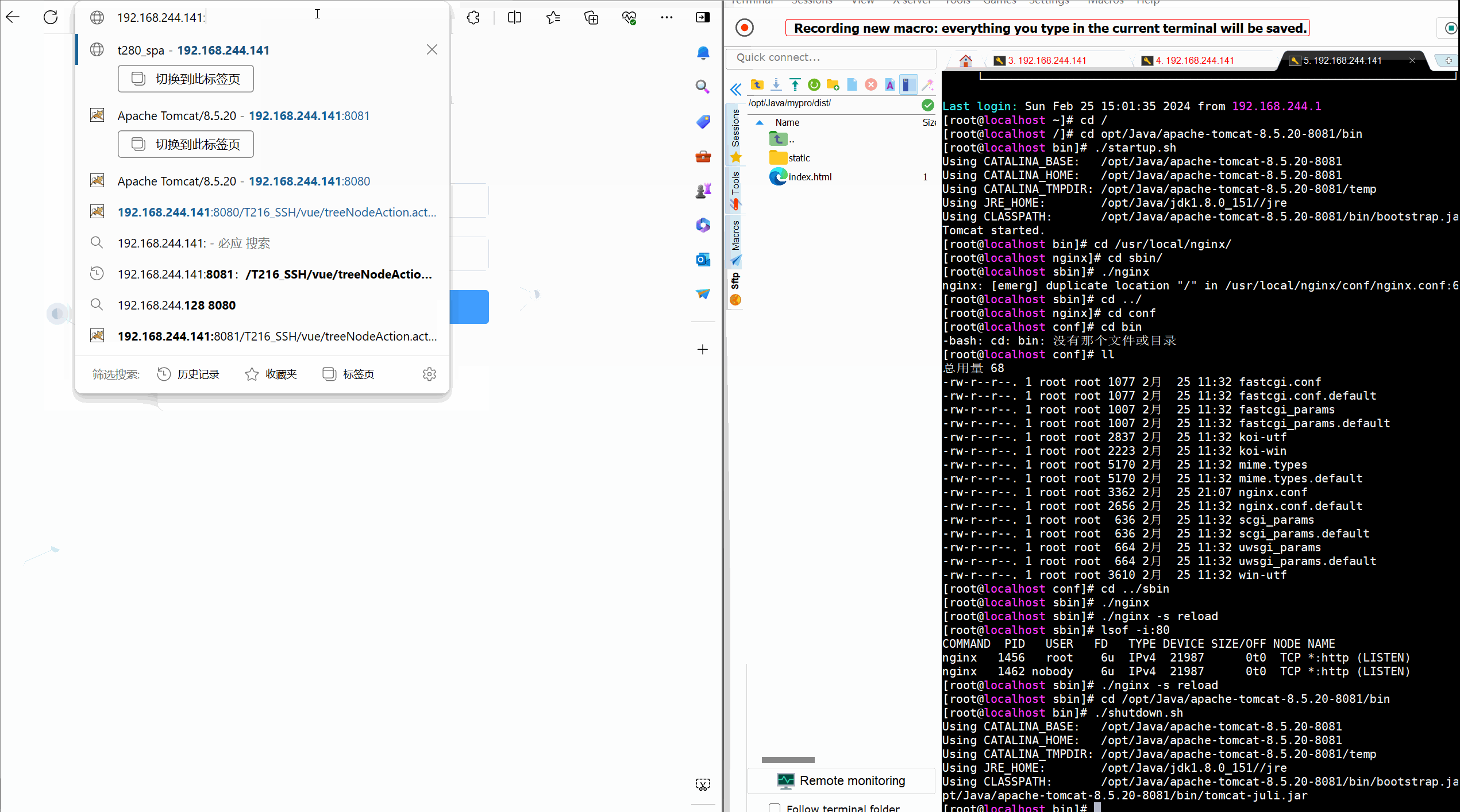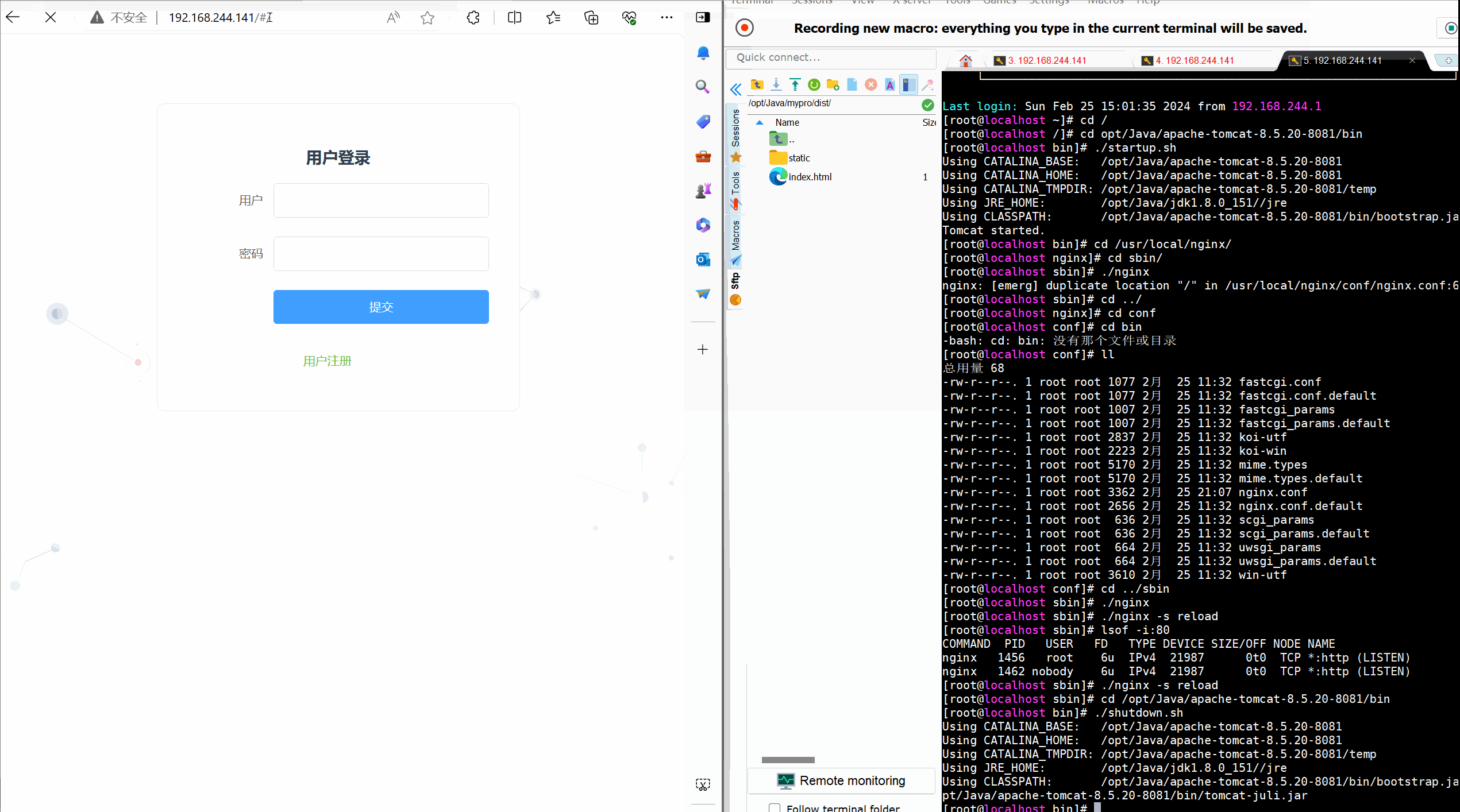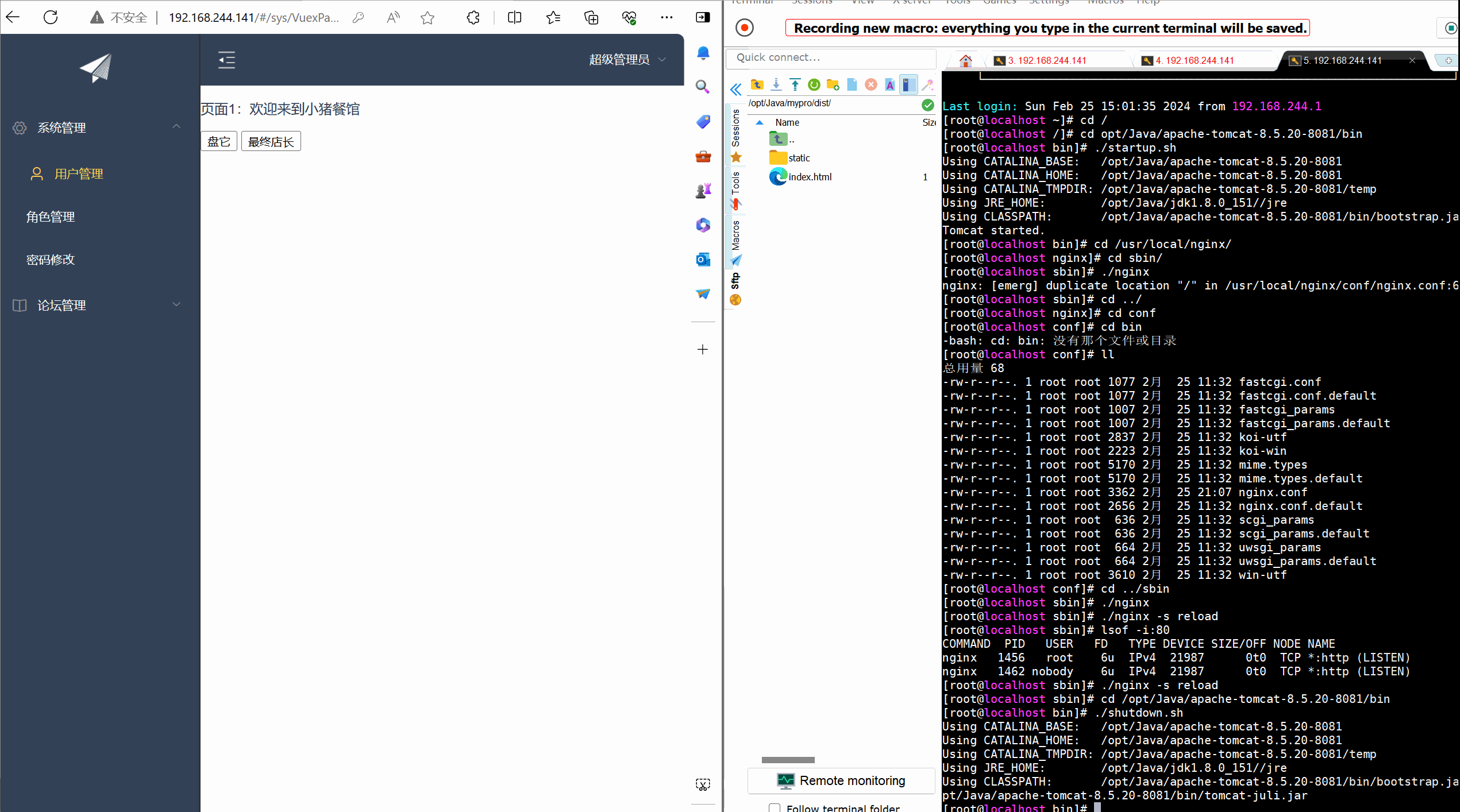
【Linux】部署前后端分离项目---(Nginx自启,负载均衡)
目录 前言 一 Nginx(自启动) 2.1 Nginx的安装 2.2 设置自启动Nginx 二 Nginx负载均衡tomcat 2.1 准备两个tomcat 2.1.1 复制tomcat 2.1.2 修改server.xml文件 2.1.3 开放端口 2.2 Nginx配置 2.2.1 修改nginx.conf文件 2.2.2 重启Nginx服务 2…...
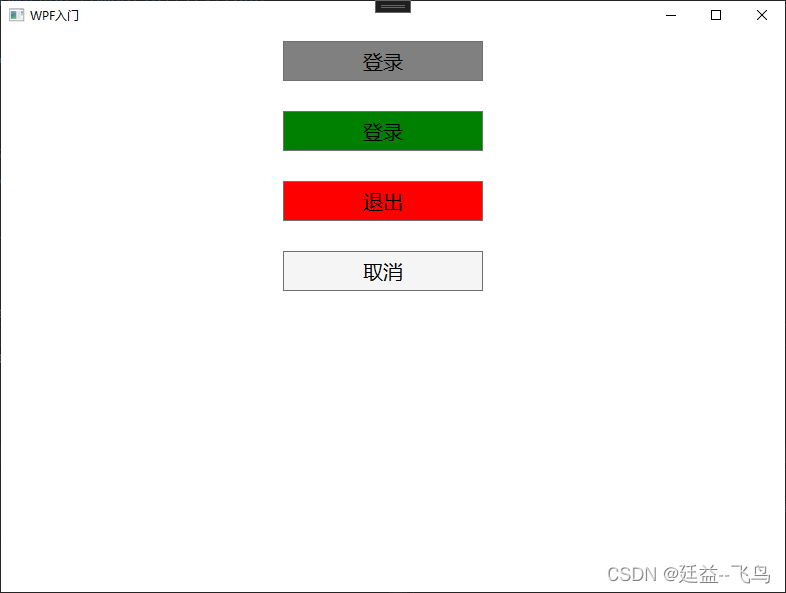
WPF Style样式设置
1.本window设置样式 <Window x:Class"WPF_Study.MainWindow"xmlns"http://schemas.microsoft.com/winfx/2006/xaml/presentation"xmlns:x"http://schemas.microsoft.com/winfx/2006/xaml"xmlns:d"http://schemas.microsoft.com/expressi…...

【STM32】软件SPI读写W25Q64芯片
目录 W25Q64模块 W25Q64芯片简介 硬件电路 W25Q64框图 Flash操作注意事项 状态寄存器 编辑 指令集 INSTRUCTIONS编辑 编辑 SPI读写W25Q64代码 硬件接线图 MySPI.c MySPI.h W25Q64 W25Q64.c W25Q64.h W25Q64_Ins.h main.c 测试 SPI通信(W25…...

普通中小学校管理信息系统V1.1
普通中小学校管理信息系统 Ordinary Primary and Secondary Schools Management Information System 普通中小学校管理信息系统 Ordinary Primary and Secondary Schools Management Information System...

中国水果采摘机器人行业市场研究及发展趋势分析报告
全版价格:壹捌零零 报告版本:下单后会更新至最新版本 交货时间:1-2天 第一章 2016-2026年中国水果采摘机器人行业总概 1.1 中国水果采摘机器人行业发展概述 机器人技术的发展是一个国家高科技水平和工业自动化程度的重要标志和体现。机器…...

Linux多进程与信号
在多进程的服务程序中,如果子进程收到退出信号,子进程自行退出。如果父进程收到退出信号,应该先向全部的子进程发送退出信号,然后自己再退出。 演示demo程序 #include <iostream> // 包含输入输出流库,用于输…...

Self-attention与Word2Vec
Self-attention(自注意力)和 Word2Vec 是两种不同的词嵌入技术,用于将单词映射到低维向量空间。它们之间的区别: Word2Vec: Word2Vec 是一种传统的词嵌入(word embedding)方法,旨在为…...
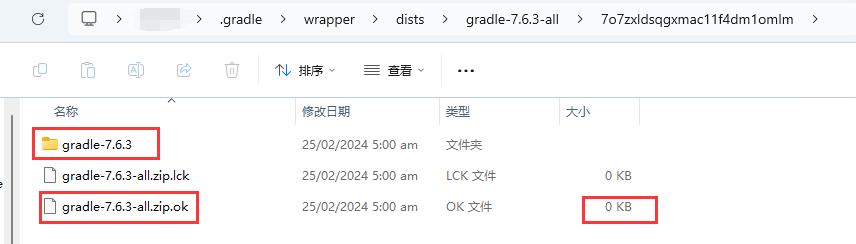
【Flutter/Android】运行到安卓手机上一直卡在 Running Gradle task ‘assembleDebug‘... 的终极解决办法
方法步骤简要 查看你的Flutter项目需要什么版本的 Gradle 插件: 下载这个插件: 方法一:浏览器输入:https://services.gradle.org/distributions/gradle-7.6.3-all.zip 方法二:去Gradle官网找对应的版本:h…...

医疗实施-客户需求分析
在我的日常系统实施过程中,总会遇到不同角色的客户提出不同类别的需求。有的需求,客户目的想提高操作便携,但会对系统稳定性存在风险,应该拒掉。有些需求紧急而且影响重大,应该紧急处理。有些需求可以做,但…...
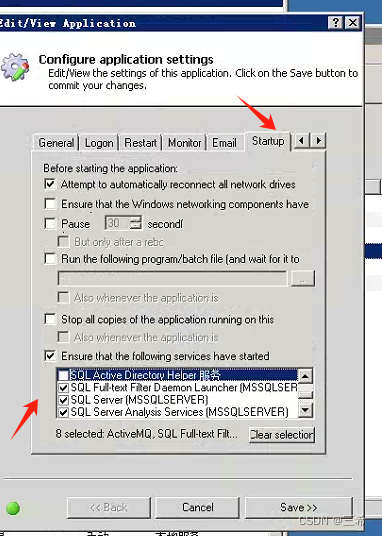
调度服务看门狗配置
查看当前服务器相关的sqlserver服务 在任务栏右键,选择点击启动任务管理器 依次点击,打开服务 找到sqlserver 相关的服务, 确认这些服务是启动状态 将相关服务在看门狗中进行配置 选择调度服务,双击打开 根据上面找的服务进行勾…...

AI时代 编程高手的秘密武器:世界顶级大学推荐的计算机教材
文章目录 01 《深入理解计算机系统》02 《算法导论》03 《计算机程序的构造和解释》04 《数据库系统概念》05 《计算机组成与设计:硬件/软件接口》06 《离散数学及其应用》07 《组合数学》08《斯坦福算法博弈论二十讲》 清华、北大、MIT、CMU、斯坦福的学霸们在新学…...

【数据结构和算法初阶(c语言)】数据结构前言,初识数据结构(给你一个选择学习数据结构和算法的理由)
1.何为数据结构 数据结构(Data Structure)是计算机存储、组织数据的方式,指相互之间存在一种或多种特定关系的 数据元素的集合。本质来讲就是在内存中去管理数据方式比如我们的增删查改。在内存中管理数据的方式有很多种(比如数组结构、链式结构、树型结…...
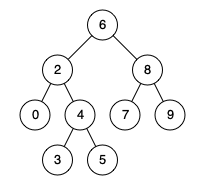
LeetCode 0235.二叉搜索树的最近公共祖先:用搜索树性质(不遍历全部节点)
【LetMeFly】235.二叉搜索树的最近公共祖先:用搜索树性质(不遍历全部节点) 力扣题目链接:https://leetcode.cn/problems/lowest-common-ancestor-of-a-binary-search-tree/ 给定一个二叉搜索树, 找到该树中两个指定节点的最近公…...

【Prometheus】概念和工作原理介绍
目录 一、概述 1.1 prometheus简介 1.2 prometheus特点 1.3 prometheus架构图 1.4 prometheus组件介绍 1、Prometheus Server 2、Client Library 3、pushgateway 4、Exporters 5、Service Discovery 6、Alertmanager 7、grafana 1.5 Prometheus 数据流向 1.6 Pro…...

四川易点慧电子商务有限公司抖音小店:可靠之选,购物新体验
在当今这个网络购物日益盛行的时代,选择一家可靠的电商平台成为了消费者最为关心的问题之一。四川易点慧电子商务有限公司抖音小店作为新兴的电商力量,凭借其独特的魅力和优势,正逐渐成为众多消费者心中的可靠之选。 易点慧电子商务有限公司在…...
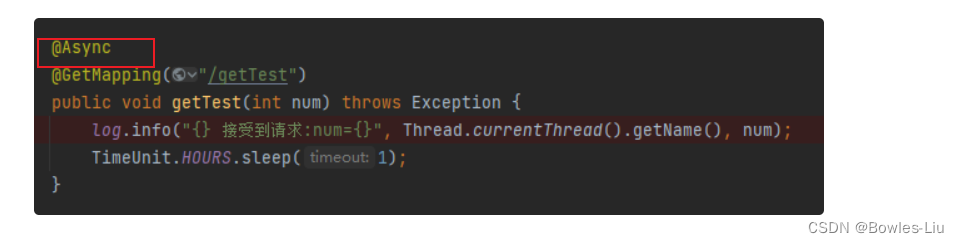
SpringBoot自带的tomcat的最大连接数和最大的并发数
先说结果:springboot自带的tomcat的最大并发数是200, 最大连接数是:max-connectionsaccept-count的值 再说一下和连接数相关的几个配置: 以下都是默认值: server.tomcat.threads.min-spare10 server.tomcat.threa…...

TLS1.2抓包解析
1.TLS1.2记录层消息解析 Transport Layer SecurityTLSv1.2 Record Layer: Handshake Protocol: Client HelloContent Type: Handshake (22)Version: TLS 1.0 (0x0301)Length: 253Content Type:消息类型,1个字节。 i 0Version:协议版本&…...
使用两个队列实现栈
在计算机科学中,栈是一种数据结构,它遵循后进先出(LIFO)的原则。这意味着最后一个被添加到栈的元素将是第一个被移除的元素。然而,Java的标准库并没有提供栈的实现,但我们可以使用两个队列来模拟一个栈的行…...
)
Spring Boot 实现流式响应(兼容 2.7.x)
在实际开发中,我们可能会遇到一些流式数据处理的场景,比如接收来自上游接口的 Server-Sent Events(SSE) 或 流式 JSON 内容,并将其原样中转给前端页面或客户端。这种情况下,传统的 RestTemplate 缓存机制会…...

【网络安全产品大调研系列】2. 体验漏洞扫描
前言 2023 年漏洞扫描服务市场规模预计为 3.06(十亿美元)。漏洞扫描服务市场行业预计将从 2024 年的 3.48(十亿美元)增长到 2032 年的 9.54(十亿美元)。预测期内漏洞扫描服务市场 CAGR(增长率&…...

蓝桥杯 2024 15届国赛 A组 儿童节快乐
P10576 [蓝桥杯 2024 国 A] 儿童节快乐 题目描述 五彩斑斓的气球在蓝天下悠然飘荡,轻快的音乐在耳边持续回荡,小朋友们手牵着手一同畅快欢笑。在这样一片安乐祥和的氛围下,六一来了。 今天是六一儿童节,小蓝老师为了让大家在节…...

C++中string流知识详解和示例
一、概览与类体系 C 提供三种基于内存字符串的流,定义在 <sstream> 中: std::istringstream:输入流,从已有字符串中读取并解析。std::ostringstream:输出流,向内部缓冲区写入内容,最终取…...

LLM基础1_语言模型如何处理文本
基于GitHub项目:https://github.com/datawhalechina/llms-from-scratch-cn 工具介绍 tiktoken:OpenAI开发的专业"分词器" torch:Facebook开发的强力计算引擎,相当于超级计算器 理解词嵌入:给词语画"…...

AI书签管理工具开发全记录(十九):嵌入资源处理
1.前言 📝 在上一篇文章中,我们完成了书签的导入导出功能。本篇文章我们研究如何处理嵌入资源,方便后续将资源打包到一个可执行文件中。 2.embed介绍 🎯 Go 1.16 引入了革命性的 embed 包,彻底改变了静态资源管理的…...

Netty从入门到进阶(二)
二、Netty入门 1. 概述 1.1 Netty是什么 Netty is an asynchronous event-driven network application framework for rapid development of maintainable high performance protocol servers & clients. Netty是一个异步的、基于事件驱动的网络应用框架,用于…...

pycharm 设置环境出错
pycharm 设置环境出错 pycharm 新建项目,设置虚拟环境,出错 pycharm 出错 Cannot open Local Failed to start [powershell.exe, -NoExit, -ExecutionPolicy, Bypass, -File, C:\Program Files\JetBrains\PyCharm 2024.1.3\plugins\terminal\shell-int…...

篇章二 论坛系统——系统设计
目录 2.系统设计 2.1 技术选型 2.2 设计数据库结构 2.2.1 数据库实体 1. 数据库设计 1.1 数据库名: forum db 1.2 表的设计 1.3 编写SQL 2.系统设计 2.1 技术选型 2.2 设计数据库结构 2.2.1 数据库实体 通过需求分析获得概念类并结合业务实现过程中的技术需要&#x…...

Java数组Arrays操作全攻略
Arrays类的概述 Java中的Arrays类位于java.util包中,提供了一系列静态方法用于操作数组(如排序、搜索、填充、比较等)。这些方法适用于基本类型数组和对象数组。 常用成员方法及代码示例 排序(sort) 对数组进行升序…...
