【数位】【数论】【分类讨论】2999. 统计强大整数的数目
作者推荐
动态规划的时间复杂度优化
本文涉及知识点
数位 数论
LeetCode2999. 统计强大整数的数目
给你三个整数 start ,finish 和 limit 。同时给你一个下标从 0 开始的字符串 s ,表示一个 正 整数。
如果一个 正 整数 x 末尾部分是 s (换句话说,s 是 x 的 后缀),且 x 中的每个数位至多是 limit ,那么我们称 x 是 强大的 。
请你返回区间 [start…finish] 内强大整数的 总数目 。
如果一个字符串 x 是 y 中某个下标开始(包括 0 ),到下标为 y.length - 1 结束的子字符串,那么我们称 x 是 y 的一个后缀。比方说,25 是 5125 的一个后缀,但不是 512 的后缀。
示例 1:
输入:start = 1, finish = 6000, limit = 4, s = “124”
输出:5
解释:区间 [1…6000] 内的强大数字为 124 ,1124 ,2124 ,3124 和 4124 。这些整数的各个数位都 <= 4 且 “124” 是它们的后缀。注意 5124 不是强大整数,因为第一个数位 5 大于 4 。
这个区间内总共只有这 5 个强大整数。
示例 2:
输入:start = 15, finish = 215, limit = 6, s = “10”
输出:2
解释:区间 [15…215] 内的强大整数为 110 和 210 。这些整数的各个数位都 <= 6 且 “10” 是它们的后缀。
这个区间总共只有这 2 个强大整数。
示例 3:
输入:start = 1000, finish = 2000, limit = 4, s = “3000”
输出:0
解释:区间 [1000…2000] 内的整数都小于 3000 ,所以 “3000” 不可能是这个区间内任何整数的后缀。
提示:
1 <= start <= finish <= 1015
1 <= limit <= 9
1 <= s.length <= floor(log10(finish)) + 1
s 数位中每个数字都小于等于 limit 。
s 不包含任何前导 0 。
数论
len1 = s.length s1 = 下届.right(len1) s2 = 上届.right(len1)
枚举合法数字的长度len2。
我们当前数字假定除掉作为后缀的s,余下的部分为x,x的len = len2- len1。统计x的可能数量。难点:上下界可能包括limit以外的数字。
分类讨论:
一,x就是下界的前缀。
二,x就是上界的前缀。
三,x同时是上下界的前缀,做特殊处理,此时情况四不会存在。return (s1<=s)&&(s <= s2);
四,x 在上下界前缀之间。
处理余下的三种情况:
一,下界的前缀不包括limit及以上数字且s1 <= s,数量+1。
二,上界的前缀不包括limit及以上数字且s <= s2,数量+1。
三,小于上界前缀的数量-小于下界前缀的数量-等于下届前缀的数量。加上s后,一定在上下界之间。
等于下届前缀的数量:如果下届前缀不包括limit及以上数字,为1;否则为0。
小于下界(上界)前缀t的数量:
小于t的数量必定有j位前缀相同,j ∈ [ 0 , l e n ) \in[0,len) ∈[0,len) 枚举j。
bitMin = (0==j)?1:0 最高位不能是0,其它位可以为0。
∑ j : 0 l e n − 1 ( m i n ( t [ j ] , l i m i t + 1 ) − b i t M i n ) × ( l i m i t + 1 ) l e n − j − 1 \sum_{j:0}^{len-1}(min(t[j],limit+1)-bitMin)\times (limit+1)^{len-j-1} ∑j:0len−1(min(t[j],limit+1)−bitMin)×(limit+1)len−j−1
就是当前位的取值数量 乘以 后面各位的取值数量。如果s[j]>=limit,则不会存在(j+1)位及更多位前缀相等。提前退出循环。
代码
核心代码
class Solution {
public:long long numberOfPowerfulInt(long long start, long long finish, int limit, string s) {m_s = s;m_limit = limit;const string strLow = std::to_string(start);const string strUp = std::to_string(finish);const int len0 = strLow.length();const int len = strUp.length(); m_vUnit.emplace_back(1);for (int i = 1; i <= 15; i++){m_vUnit.emplace_back(m_vUnit.back() * (limit+1));}if (len0 == len){return Do(strLow, strUp);}long long llRet = 0;llRet += Do(strLow, string(len0, limit+ '0'));for (int i = len0+1; i < len; i++){llRet += Do(("1" + string(i - 1, '0')).c_str(), string(i, limit + '0').c_str());} llRet +=Do (("1" + string(len - 1, '0')).c_str(), strUp.c_str());return llRet;}long long Do(string strLow, string strUp){const int len = strLow.length() - m_s.length();if (len < 0 ){return 0;}auto [llCnt1, bVilid1] = LessEqual(len, strLow);auto [llCnt2, bVilid2] = LessEqual(len, strUp);bool b1 = (strLow.substr(len) <= m_s) && (bVilid1);bool b2 = (strUp.substr(len) >= m_s) && (bVilid2);if (strLow.substr(0,len) == strUp.substr(0,len)){return b1 && b2;}return (llCnt2 - llCnt1 - (bVilid1&&len)) + b1 + b2;}std::pair<long long, bool> LessEqual(int len,const string& s ){bool bVilid = true;long long llCnt = 0;for (int i = 0; i < len; i++){//计算小于数量const int bitMin = (0 == i) ? 1 : 0;if (bVilid){llCnt += (min(s[i] - '0', m_limit + 1) - bitMin) * m_vUnit[len - i - 1];}if (s[i] > m_limit + '0'){bVilid = false;} }return make_pair(llCnt, bVilid);}vector<long long> m_vUnit;string m_s;int m_limit;
};
测试用例
template<class T,class T2>
void Assert(const T& t1, const T2& t2)
{assert(t1 == t2);
}template<class T>
void Assert(const vector<T>& v1, const vector<T>& v2)
{if (v1.size() != v2.size()){assert(false);return;}for (int i = 0; i < v1.size(); i++){Assert(v1[i], v2[i]);}}int main()
{long long start, finish;int limit;string s;{Solution sln;start = 1, finish = 1000000000000000, limit = 5, s = "1000000000000000";auto res = sln.numberOfPowerfulInt(start, finish, limit, s);Assert(1, res);}{Solution sln;start = 1829505, finish = 1955574, limit = 7, s = "11223";auto res = sln.numberOfPowerfulInt(start, finish, limit, s);Assert(0, res);}{Solution sln;start = 5398, finish = 6415, limit = 8, s = "101";auto res = sln.numberOfPowerfulInt(start, finish, limit, s);Assert(1, res);}{Solution sln;start = 1, finish = 6000, limit = 4, s = "124";auto res = sln.numberOfPowerfulInt(start, finish, limit, s);Assert(5, res);}{Solution sln;start = 15, finish = 215, limit = 6, s = "10";auto res = sln.numberOfPowerfulInt(start, finish, limit, s);Assert(2, res);}{Solution sln;start = 10, finish = 1844, limit = 5, s = "12";auto res = sln.numberOfPowerfulInt(start, finish, limit, s);Assert(12, res);}{Solution sln;start = 1, finish = 2000, limit = 8, s = "1";auto res = sln.numberOfPowerfulInt(start, finish, limit, s);Assert(162, res);}{Solution sln;start = 1829505, finish = 1255574165, limit =7, s = "11223";auto res = sln.numberOfPowerfulInt(start, finish, limit, s);Assert(5470, res);}{Solution sln;start = 15398, finish = 1424153842, limit = 8, s = "101";auto res = sln.numberOfPowerfulInt(start, finish, limit, s);Assert(783790, res);}}
优化
n位数,可以看成包括(m-n)个前置0的m位数。
class Solution {
public:long long numberOfPowerfulInt(long long start, long long finish, int limit, string s) {m_s = s;m_limit = limit;string strLow = std::to_string(start);const string strUp = std::to_string(finish);if (strLow.length() < strUp.length()){strLow = string(strUp.length() - strLow.length(), '0')+strLow;} m_vUnit.emplace_back(1);for (int i = 1; i <= 15; i++){m_vUnit.emplace_back(m_vUnit.back() * (limit+1));}return Do(strLow, strUp);}long long Do(string strLow, string strUp){const int len = strLow.length() - m_s.length();if (len < 0 ){return 0;}auto [llCnt1, bVilid1] = LessEqual(len, strLow);auto [llCnt2, bVilid2] = LessEqual(len, strUp);bool b1 = (strLow.substr(len) <= m_s) && (bVilid1);bool b2 = (strUp.substr(len) >= m_s) && (bVilid2);if (strLow.substr(0,len) == strUp.substr(0,len)){return b1 && b2;}return (llCnt2 - llCnt1 - (bVilid1&&len)) + b1 + b2;}std::pair<long long, bool> LessEqual(int len,const string& s ){bool bVilid = true;long long llCnt = 0;for (int i = 0; i < len; i++){//计算小于数量if (bVilid){llCnt += (min(s[i] - '0', m_limit + 1) - 0) * m_vUnit[len - i - 1];}if (s[i] > m_limit + '0'){bVilid = false;} }return make_pair(llCnt, bVilid);}vector<long long> m_vUnit;string m_s;int m_limit;
};
相关文章:

【数位】【数论】【分类讨论】2999. 统计强大整数的数目
作者推荐 动态规划的时间复杂度优化 本文涉及知识点 数位 数论 LeetCode2999. 统计强大整数的数目 给你三个整数 start ,finish 和 limit 。同时给你一个下标从 0 开始的字符串 s ,表示一个 正 整数。 如果一个 正 整数 x 末尾部分是 s (…...

MongoDB聚合运算符:$atan2
$atan2用来计算反正切,返回指定表达式的反正切值,与$antan的区别主要是参数不同。 语法 { $atan2: [<expression1>, <expression1>] }<expression>为可被解析为数值的表达式$atan2返回弧度,使用$radiansToDegrees运算符可…...

敏捷开发最佳实践:价值维度实践案例之ABTest中台化
22年敏捷白皮书调研发现,仅有14%的企业部分实现价值管理闭环,8%的企业能够做到企业战略和业务目标与价值管理紧密结合。这一现象说明了大部分中国企业还不能在敏捷实践中实现需求价值的体系化及多维度价值度量,因此推广优秀的敏捷实践至关重要…...
爬虫基本库的使用(requests库的详细解析)
注:本文一共4万多字,希望读者能耐心读完!!! 前面,我们了解了urllib库的基本用法(爬虫基本库的使用(urllib库的详细解析)-CSDN博客)。其中,确实又不方便的地方。例如处理网页验证…...
QT实现串口通信
一.Qt串口通信 Qt提供了两个关于串口通信的C类,分别是QSerialPort和QSerialPortInfo。 QSerialPort类提供了操作串口的各种接口。 QSerialPortInfo是一个辅助类,可以提供计算机中可用的串口的各种信息。 QSerialPortInfo Class用于提供外部串行端口的…...
)
微信小程序 --- 通用模块封装(showToast,showModal ,本地存储)
目录 01. 为什么进行模块封装 02. 消息提示模块封装 03. 模态对话框封装 04. 封装本地存储 API 05. 拓展:封装异步存储API优化代码 01. 为什么进行模块封装 在进行项目开发的时候,我们经常的会频繁的使用到一些 API, 例如:wx.showToast…...
基于springboot+vue的音乐网站(前后端分离)
博主主页:猫头鹰源码 博主简介:Java领域优质创作者、CSDN博客专家、阿里云专家博主、公司架构师、全网粉丝5万、专注Java技术领域和毕业设计项目实战,欢迎高校老师\讲师\同行交流合作 主要内容:毕业设计(Javaweb项目|小程序|Pyt…...
pclpy 最小二乘法拟合平面
pclpy 最小二乘法拟合平面 一、算法原理二、代码三、结果1.左边原点云、右边最小二乘法拟合平面后点云投影 四、相关数据 一、算法原理 平面方程的一般表达式为: A x B y C z D 0 ( C ≠ 0 ) Ax By Cz D 0 \quad (C\neq0) AxByCzD0(C0) 即: …...

蓝桥杯备战刷题(自用)
1.被污染的支票 #include <iostream> #include <vector> #include <map> #include <algorithm> using namespace std; int main() {int n;cin>>n;vector<int>L;map<int,int>mp;bool ok0;int num;for(int i1;i<n;i){cin>>nu…...
Python习题详解
练习: 1,计算100以内奇数的和 #计算100以内所有奇数的和 sum 0 # n 1 # while n < 100: # # sum sum n # sum n # # n n 2 # n 2 # print(sum) n 99 #求偶数时n 100 while n > 0:sum n# n n - 2n - 2 print(sum)2,打印直…...
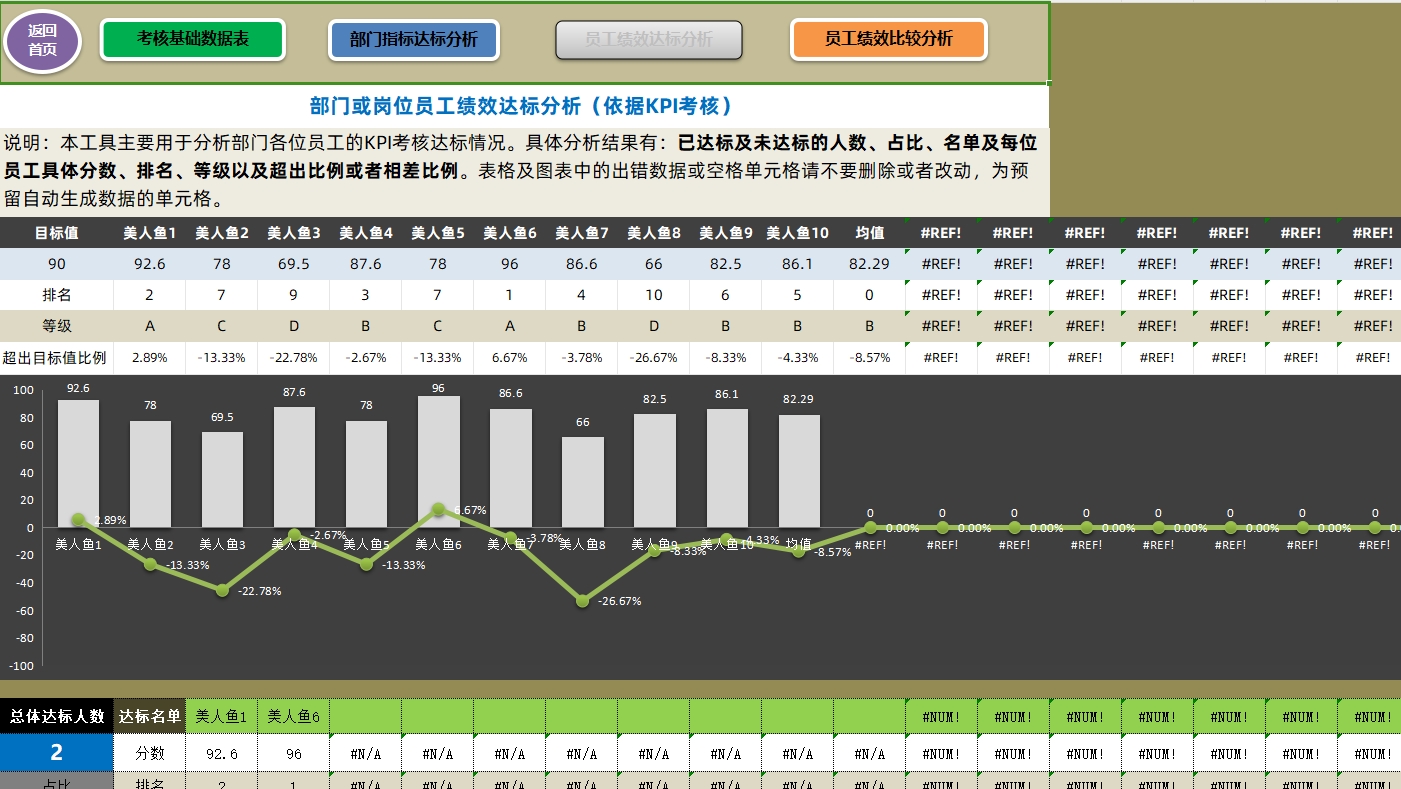
绩效考核利器:Excel报表模板,解锁企业高效员工评价新境界
一、背景与目标 在现今的企业管理中,绩效考核是一项至关重要的任务。它旨在评估员工的工作表现,激励员工积极进取,同时也是制定薪酬、晋升、培训等决策的重要依据。为了满足这一需求,我们设计了一款绩效考核Excel报表模板&#x…...

如何使用Lychee+cpolar搭建本地私人图床并实现远程访问存储图片
文章目录 1.前言2. Lychee网站搭建2.1. Lychee下载和安装2.2 Lychee网页测试2.3 cpolar的安装和注册 3.本地网页发布3.1 Cpolar云端设置3.2 Cpolar本地设置 4.公网访问测试5.结语 1.前言 图床作为图片集中存放的服务网站,可以看做是云存储的一部分,既可…...
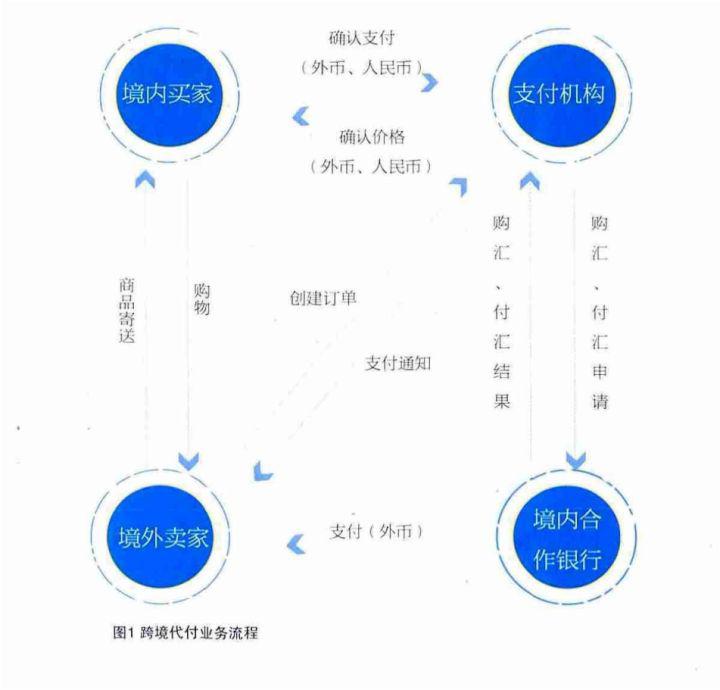
跨境支付介绍
1、跨境电商定义和分类; 2、国际贸易清结算; 3、跨境支付; 1、跨境电商定义和分类 跨境电商业务简单说就是指不同国家地域的主体通过电子商务进行交易的一种业务模式。同传统的电商不同,交易双方属于不同的国家。因此࿰…...
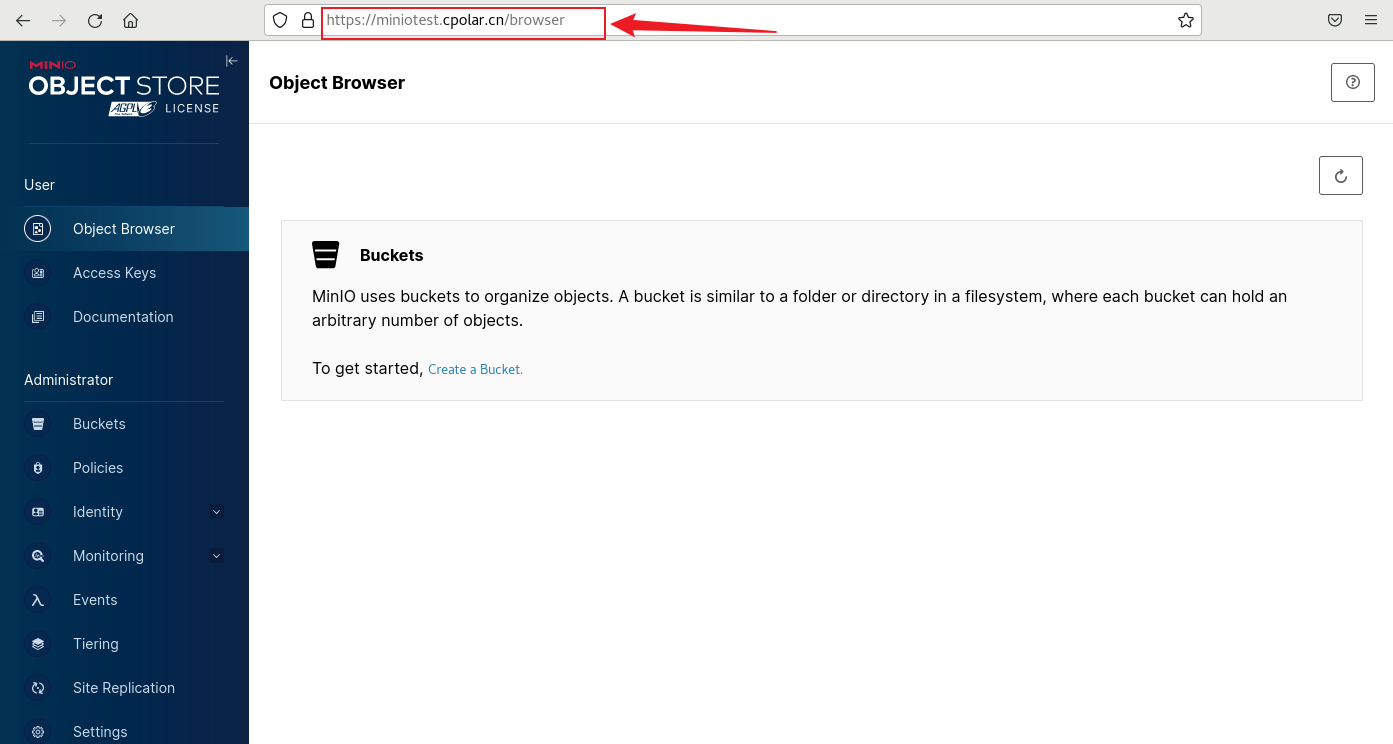
如何在Linux搭建MinIO服务并实现无公网ip远程访问内网管理界面
文章目录 前言1. Docker 部署MinIO2. 本地访问MinIO3. Linux安装Cpolar4. 配置MinIO公网地址5. 远程访问MinIO管理界面6. 固定MinIO公网地址 前言 MinIO是一个开源的对象存储服务器,可以在各种环境中运行,例如本地、Docker容器、Kubernetes集群等。它兼…...
Cortex-M可以跑Linux操作系统吗?
在开始前我有一些资料,是我根据网友给的问题精心整理了一份「Linux的资料从专业入门到高级教程」, 点个关注在评论区回复“888”之后私信回复“888”,全部无偿共享给大家!!! Cortex-M系列微控制器主要设计…...
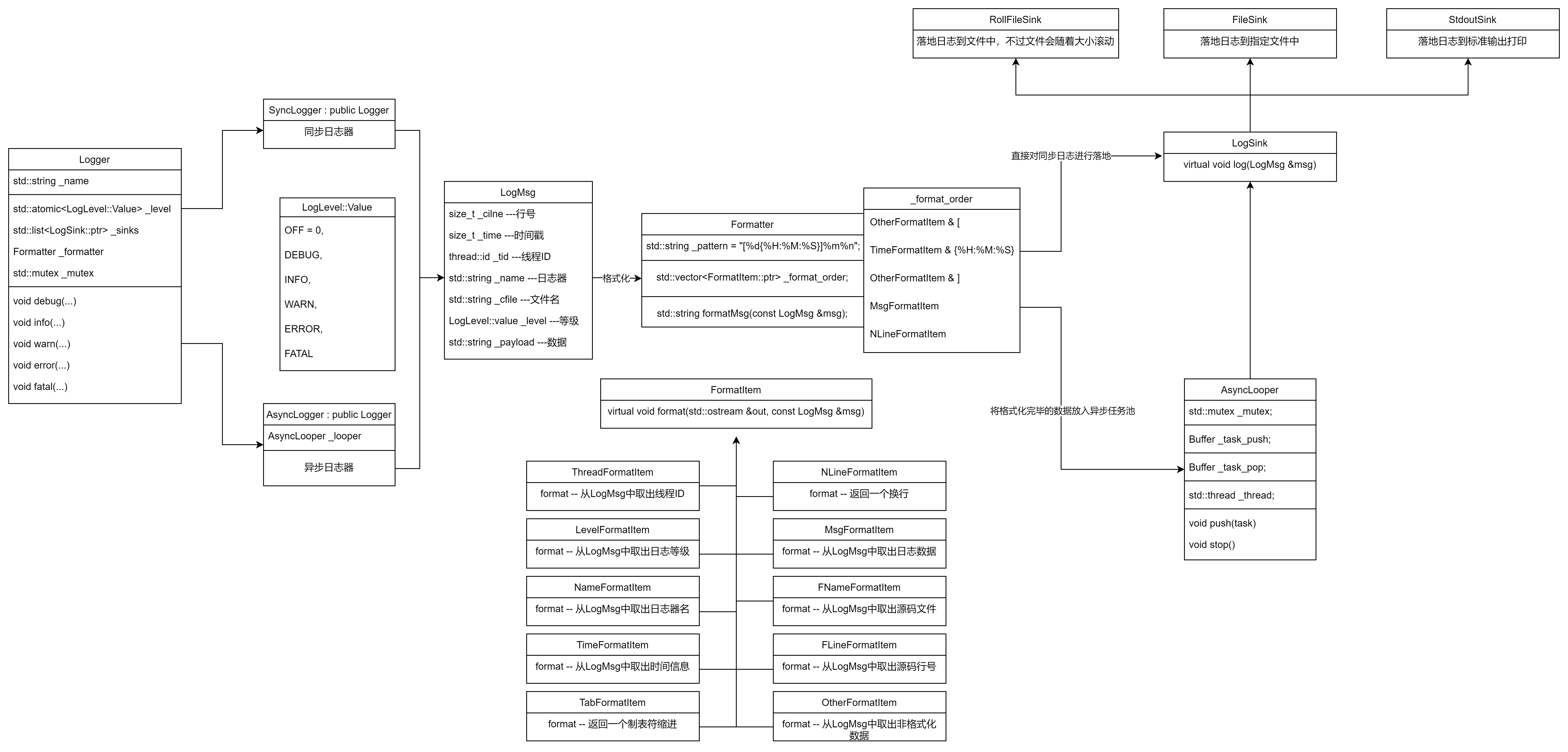
日志系统项目(2)项目实现(实用工具类、日志等级类、日志消息类、日志格式化输出类)
前面的文章中我们讲述了日志系统项目的前置知识点,再本文中我们将开始日志项目的细节实现。 日志系统框架设计 本项目实现的是一个多日志器日志系统,主要实现的功能是让程序员能够轻松的将程序运行日志信息落地到指定的位置,且支持同步与异…...

剑指offer面试题19 二叉树的镜像
考察点 树的遍历知识点 题目 分析 我们分析算法题目的思路基本上都是归纳法,即通过举一些普通的例子来推理出算法流程,而画图又是举例子的常用手段,比如针对树或者链表画画图,针对数字类的举一些数字的例子寻找规律,…...
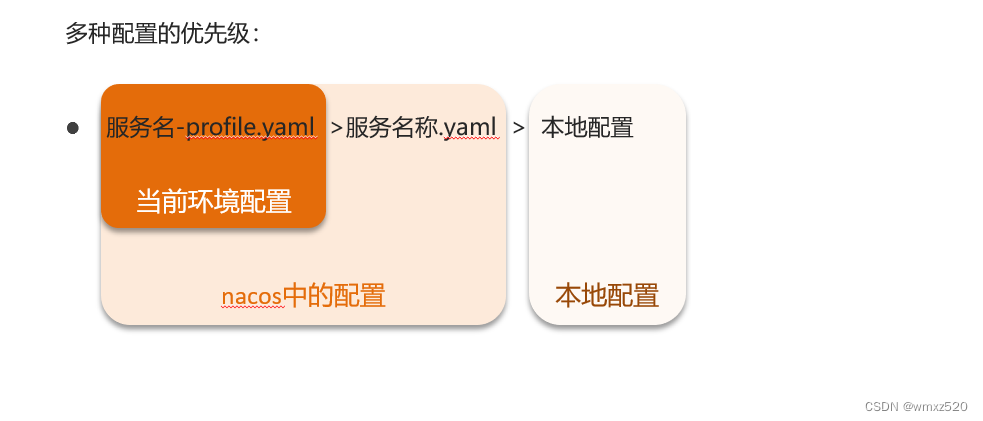
SpringCloud Alibaba 2022之Nacos学习
SpringCloud Alibaba 2022使用 SpringCloud Alibaba 2022需要Spring Boot 3.0以上的版本,同时JDK需要是17及以上的版本。具体的可以看官网的说明。 Spring Cloud Alibaba版本说明 环境搭建 这里搭建的是一个聚合项目。项目结构如下: 父项目的pom.xm…...

js之数组遍历
for 可以用来遍历数组、字符串、类数组、DOM节点,可以更改原数组,可以使用break、continue 跳出循环 return 只能在函数内部使用 for(声明循环变量;判断循环条件;更新循环变量){循环体 }forEach 参数(当前元素&#x…...

极狐GitLab 16.9 重磅发布,快来 pick 你心仪的功能吧~【五】
GitLab 是一个全球知名的一体化 DevOps 平台,很多人都通过私有化部署 GitLab 来进行源代码托管。极狐GitLab 是 GitLab 在中国的发行版,专门为中国程序员服务。可以一键式部署极狐GitLab。 沿袭我们的月度发版机制,今天我们正式发布极狐GitL…...

AI Agent与Agentic AI:原理、应用、挑战与未来展望
文章目录 一、引言二、AI Agent与Agentic AI的兴起2.1 技术契机与生态成熟2.2 Agent的定义与特征2.3 Agent的发展历程 三、AI Agent的核心技术栈解密3.1 感知模块代码示例:使用Python和OpenCV进行图像识别 3.2 认知与决策模块代码示例:使用OpenAI GPT-3进…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院查看报告小程序
一、开发环境准备 工具安装: 下载安装DevEco Studio 4.0(支持HarmonyOS 5)配置HarmonyOS SDK 5.0确保Node.js版本≥14 项目初始化: ohpm init harmony/hospital-report-app 二、核心功能模块实现 1. 报告列表…...

学习STC51单片机31(芯片为STC89C52RCRC)OLED显示屏1
每日一言 生活的美好,总是藏在那些你咬牙坚持的日子里。 硬件:OLED 以后要用到OLED的时候找到这个文件 OLED的设备地址 SSD1306"SSD" 是品牌缩写,"1306" 是产品编号。 驱动 OLED 屏幕的 IIC 总线数据传输格式 示意图 …...

EtherNet/IP转DeviceNet协议网关详解
一,设备主要功能 疆鸿智能JH-DVN-EIP本产品是自主研发的一款EtherNet/IP从站功能的通讯网关。该产品主要功能是连接DeviceNet总线和EtherNet/IP网络,本网关连接到EtherNet/IP总线中做为从站使用,连接到DeviceNet总线中做为从站使用。 在自动…...

数据库分批入库
今天在工作中,遇到一个问题,就是分批查询的时候,由于批次过大导致出现了一些问题,一下是问题描述和解决方案: 示例: // 假设已有数据列表 dataList 和 PreparedStatement pstmt int batchSize 1000; // …...

Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决
Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决 问题背景 在一个基于 Spring Cloud Gateway WebFlux 构建的微服务项目中,新增了一个本地验证码接口 /code,使用函数式路由(RouterFunction)和 Hutool 的 Circle…...

vulnyx Blogger writeup
信息收集 arp-scan nmap 获取userFlag 上web看看 一个默认的页面,gobuster扫一下目录 可以看到扫出的目录中得到了一个有价值的目录/wordpress,说明目标所使用的cms是wordpress,访问http://192.168.43.213/wordpress/然后查看源码能看到 这…...

基于Springboot+Vue的办公管理系统
角色: 管理员、员工 技术: 后端: SpringBoot, Vue2, MySQL, Mybatis-Plus 前端: Vue2, Element-UI, Axios, Echarts, Vue-Router 核心功能: 该办公管理系统是一个综合性的企业内部管理平台,旨在提升企业运营效率和员工管理水…...

Golang——6、指针和结构体
指针和结构体 1、指针1.1、指针地址和指针类型1.2、指针取值1.3、new和make 2、结构体2.1、type关键字的使用2.2、结构体的定义和初始化2.3、结构体方法和接收者2.4、给任意类型添加方法2.5、结构体的匿名字段2.6、嵌套结构体2.7、嵌套匿名结构体2.8、结构体的继承 3、结构体与…...

什么是VR全景技术
VR全景技术,全称为虚拟现实全景技术,是通过计算机图像模拟生成三维空间中的虚拟世界,使用户能够在该虚拟世界中进行全方位、无死角的观察和交互的技术。VR全景技术模拟人在真实空间中的视觉体验,结合图文、3D、音视频等多媒体元素…...
