回归预测 | Matlab实现PSO-BiLSTM-Attention粒子群算法优化双向长短期记忆神经网络融合注意力机制多变量回归预测
回归预测 | Matlab实现PSO-BiLSTM-Attention粒子群算法优化双向长短期记忆神经网络融合注意力机制多变量回归预测
目录
- 回归预测 | Matlab实现PSO-BiLSTM-Attention粒子群算法优化双向长短期记忆神经网络融合注意力机制多变量回归预测
- 预测效果
- 基本描述
- 程序设计
- 参考资料
预测效果






基本描述
1.Matlab实现PSO-BiLSTM-Attention多变量回归预测,粒子群算法优化双向长短期记忆神经网络融合注意力机制;
粒子群算法优化BiLSTM的学习率,隐藏层节点,正则化系数;
多头自注意力层 (Multihead-Self-Attention):Multihead-Self-Attention多头注意力机制是一种用于模型关注输入序列中不同位置相关性的机制。它通过计算每个位置与其他位置之间的注意力权重,进而对输入序列进行加权求和。注意力能够帮助模型在处理序列数据时,对不同位置的信息进行适当的加权,从而更好地捕捉序列中的关键信息。在时序预测任务中,注意力机制可以用于对序列中不同时间步之间的相关性进行建模。
2.运行环境为Matlab2023a及以上;
3.输入多个特征,输出单个变量,多变量回归预测;
4.data为数据集,main.m为主程序,运行即可,所有文件放在一个文件夹;
5.命令窗口输出R2、MSE、MAE、MAPE和MBE多指标评价;
程序设计
- 完整程序和数据获取方式资源出下载Matlab实现PSO-BiLSTM-Attention粒子群算法优化双向长短期记忆神经网络融合注意力机制多变量回归预测。
%% 参数设置
%% 清空环境变量
warning off % 关闭报警信息
close all % 关闭开启的图窗
clear % 清空变量
clc % 清空命令行
tic
% restoredefaultpath%% 导入数据
res =xlsread('data.xlsx','sheet1','A2:H104');%% 数据分析
num_size = 0.7; % 训练集占数据集比例
outdim = 1; % 最后一列为输出
num_samples = size(res, 1); % 样本个数
res = res(randperm(num_samples), :); % 打乱数据集(不希望打乱时,注释该行)
num_train_s = round(num_size * num_samples); % 训练集样本个数
f_ = size(res, 2) - outdim; % 输入特征维度%% 划分训练集和测试集
P_train = res(1: num_train_s, 1: f_)';
T_train = res(1: num_train_s, f_ + 1: end)';
M = size(P_train, 2);P_test = res(num_train_s + 1: end, 1: f_)';
T_test = res(num_train_s + 1: end, f_ + 1: end)';
N = size(P_test, 2);
%% 数据归一化
[P_train, ps_input] = mapminmax(P_train, 0, 1);
P_test = mapminmax('apply', P_test, ps_input);[t_train, ps_output] = mapminmax(T_train, 0, 1);
t_test = mapminmax('apply', T_test, ps_output);%% 划分训练集和测试集
M = size(P_train, 2);
N = size(P_test, 2);
%% 数据平铺
% 将数据平铺成1维数据只是一种处理方式
% 也可以平铺成2维数据,以及3维数据,需要修改对应模型结构
% 但是应该始终和输入层数据结构保持一致
P_train = double(reshape(P_train,f_, 1, 1, M));
P_test = double(reshape(P_test ,f_, 1, 1, N));t_train = t_train';
t_test = t_test' ;%% 数据格式转换
for i = 1 : Mp_train{i, 1} = P_train(:, :, 1, i);
endfor i = 1 : Np_test{i, 1} = P_test( :, :, 1, i);
end%% 优化函数
fobj = @(x)fical(x);
%% 优化算法参数设置
pop = 5; % 数量
Max_iter = 8; % 最大迭代次数
dim = 3; % 优化参数个数
lb = [1e-3, 32, 1e-3]; % 参数取值下界(学习率,批大小,正则化系数)
参考资料
[1] https://blog.csdn.net/kjm13182345320/article/details/129036772?spm=1001.2014.3001.5502
[2] https://blog.csdn.net/kjm13182345320/article/details/128690229
相关文章:

回归预测 | Matlab实现PSO-BiLSTM-Attention粒子群算法优化双向长短期记忆神经网络融合注意力机制多变量回归预测
回归预测 | Matlab实现PSO-BiLSTM-Attention粒子群算法优化双向长短期记忆神经网络融合注意力机制多变量回归预测 目录 回归预测 | Matlab实现PSO-BiLSTM-Attention粒子群算法优化双向长短期记忆神经网络融合注意力机制多变量回归预测预测效果基本描述程序设计参考资料 预测效果…...

[算法沉淀记录] 排序算法 —— 堆排序
排序算法 —— 堆排序 算法基础介绍 堆排序(Heap Sort)是一种基于比较的排序算法,它利用堆这种数据结构来实现排序。堆是一种特殊的完全二叉树,其中每个节点的值都必须大于或等于(最大堆)或小于或等于&am…...

C++ //练习 9.33 在本节最后一个例子中,如果不将insert的结果赋予begin,将会发生什么?编写程序,去掉此赋值语句,验证你的答案。
C Primer(第5版) 练习 9.33 练习 9.33 在本节最后一个例子中,如果不将insert的结果赋予begin,将会发生什么?编写程序,去掉此赋值语句,验证你的答案。 环境:Linux Ubuntu࿰…...
[corCTF 2022] CoRJail: From Null Byte Overflow To Docker Escape
前言 题目来源:竞赛官网 – 建议这里下载,文件系统/带符号的 vmlinux 给了 参考 [corCTF 2022] CoRJail: From Null Byte Overflow To Docker Escape Exploiting poll_list Objects In The Linux Kernel – 原作者文章,poll_list 利用方式…...
thinkphp6定时任务
这里主要是教没有用过定时任务没有头绪的朋友, 定时任务可以处理一些定时备份数据库等一系列操作, 具体根据自己的业务逻辑进行更改 直接上代码 首先, 是先在 tp 中的 command 方法中声明, 如果没有就自己新建一个, 代码如下 然后就是写你的业务逻辑 执行定时任务 方法写好了…...
)
支持国密ssl的curl编译和测试验证(上)
目录 1. 编译铜锁ssl库2. 编译nghttp2库3. 编译curl4. 验证4.1 查看版本信息4.2 验证国密ssl握手功能4.3 验证http2协议功能 以下以ubuntu 22.04环境为例进行编译 本次编译采用铜锁sslnghttp2curl,使得编译出来的curl可以支持国密ssl,并且可以支持http2…...

包装类详解
概述 Java提供了两个类型系统,基本类型与引用类型,使用基本类型在于效率,然而很多情况,会创建对象使用,因为对象可以做更多的功能,如果想要我们的基本类型像对象一样操作,就可以使用基本类型对…...

vue3与vue2的区别
Vue 3和Vue 2在以下几个方面有一些区别: 性能提升:Vue 3对渲染性能和内存占用进行了优化,使用了Proxy代理对象,比Vue 2的Object.defineProperty更高效。此外,Vue 3还引入了静态树提升(Static Tree Hoisting…...
SSL OV证书和DV、EV证书的区别
在网站搭建的过程中和小程序开发过程中,很难免会有需要用到SSL证书的地方,但是目前数字证书种类繁多,该选择什么类型的证书成为了一个令人纠结的问题。 目前在市场上较为常见的证书分为三种:DV域名验证型证书;OV组织验…...
一款.NET下 WPF UI框架介绍
WPF开源的UI框架有很多,如HandyControl、MahApps.Metro、Xceed Extended WPF Toolkit™、Modern UI for WPF (MUI)、Layui-WPF、MaterialDesignInXamlToolkit、等等,今天小编带大家认识一款比较常用的kaiyuanUI---WPF UI,这款ui框架美观现代化,用起来也超级方便, 界面展示…...
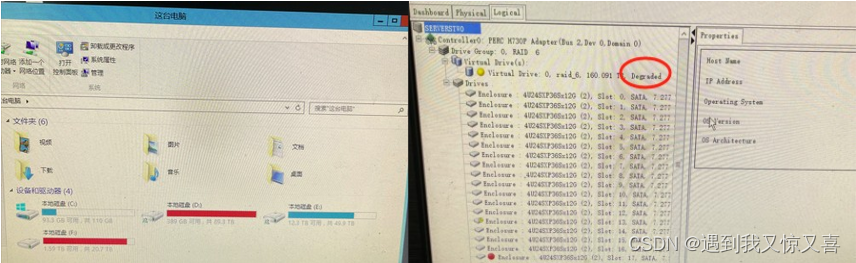
东莞IBM服务器维修之IBM x3630 M4阵列恢复
记录东莞某抖音电商公司送修一台IBM SYSTEM X3630 M4文档服务器RAID6故障导致数据丢失的恢复案例 时间:2024年02月20日, 服务器品牌:IBM System x3630 M4,阵列卡用的是DELL PERC H730P 服务器用途和用户位置:某抖音电…...
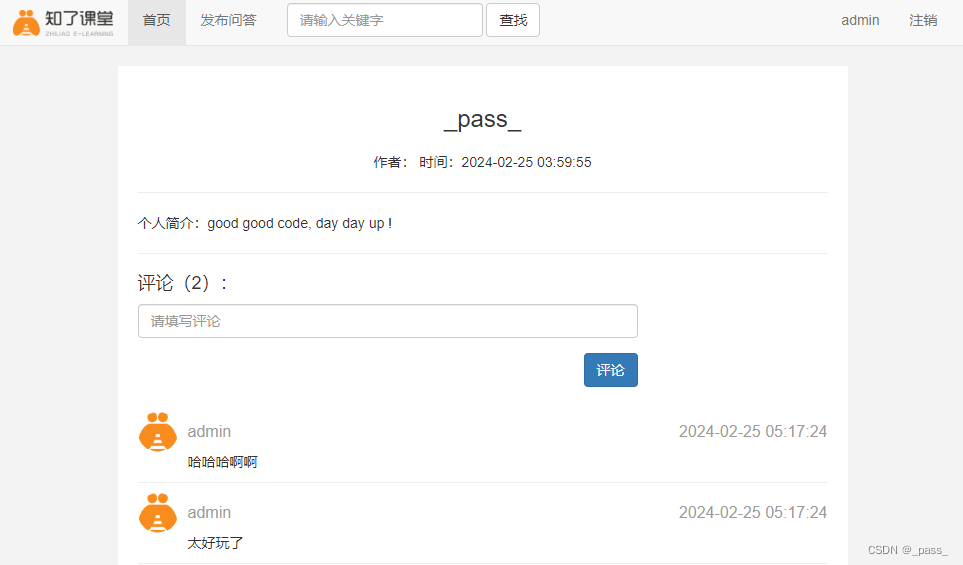
Flask基础学习4
19-【实战】问答平台项目结构搭建_剪_哔哩哔哩_bilibili 参考如上大佬的视频教程,本博客仅当学习笔记,侵权请联系删除 问答发布的web前端页面实现 register.html {% extends base.html %}{% block head %}<link rel"stylesheet" href&q…...
mac安装zookeeper
下载地址: http://archive.apache.org/dist/zookeeper/ 注意:由于Zookeeper从3.5.5版本开始,带有bin名称的包才是我们想要的下载可以直接使用的里面有编译后的二进制的包,而之前的普通的tar.gz的包里面是只是源码的包无法直接使…...

IT资讯——全速推进“AI+鸿蒙”战略布局!
文章目录 每日一句正能量前言坚持长期研发投入全速推进“AI鸿蒙”战略 人才战略新章落地持续加码核心技术生态建设 后记 每日一句正能量 人总要咽下一些委屈,然后一字不提的擦干眼泪往前走,没有人能像白纸一样没有故事,成长的代价就是失去原来…...
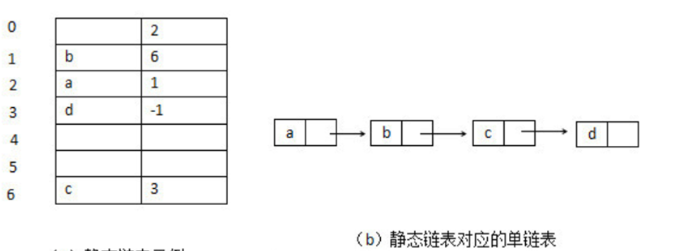
数据结构知识点总结-线性表(3)-双向链表定义、循环单链表、、循环双向链表、静态链表、顺序表与链表的比较
双向链表定义 单链表结点中只有一个指向其后继的指针,这使得单链表只能从头结点依次顺序地向后遍历。若要访问某个结点的前驱结点(插入、删除操作时),只能从头开始遍历,访问后继结点的时间复杂度为 O(1) , …...

JAVA学习-控制执行流程.for
在Java中,for循环是一种常用的控制执行流程的循环语句。它允许我们重复执行一段代码,直到满足指定的循环条件。 一、for循环的基本语法如下: for (初始化语句; 循环条件; 循环后操作) {// 循环体,要执行的代码} 其中,…...
面试总结之JVM入门
文章目录 🐒个人主页🏅JavaEE系列专栏📖前言:🎀你为什么要学习JVM?🎀JVM的作用 🎀JVM的构成(5大类)🏨1.类加载系统🐕类什么时候会被加…...
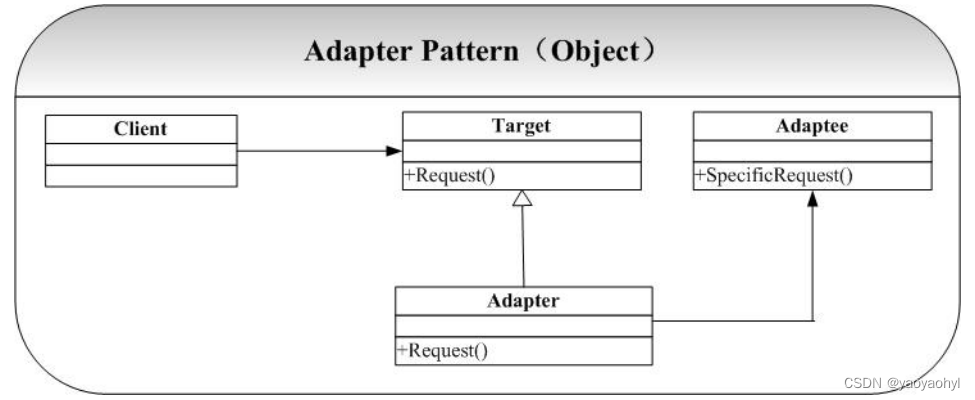
适配器模式(Adapter Pattern) C++
上一节:原型模式(Prototype Pattern) C 文章目录 0.理论1.组件2.类型3.什么时候使用 1.实践1.基础接口和类2.类适配器实现3.对象适配器实现 0.理论 适配器模式(Adapter Pattern)是一种结构型设计模式,它允…...

【程序员英语】【美语从头学】初级篇(入门)(笔记)Lesson 16 At the Shoe Store 在鞋店
《美语从头学初级入门篇》 注意:被 删除线 划掉的不一定不正确,只是不是标准答案。 文章目录 Lesson 16 At the Shoe Store 在鞋店对话A对话B笔记会话A会话B替换 Lesson 16 At the Shoe Store 在鞋店 对话A A: Do you have these shoes in size 8? B:…...

嵌入式系统在物联网中的应用与发展趋势
嵌入式系统在物联网中的应用与发展趋势 嵌入式系统在物联网中扮演着至关重要的角色,它们是连接物理世界和数字世界的桥梁,实现了物体之间的互联互通。以下是嵌入式系统在物联网中的应用与发展趋势的几个方面: 1. 应用领域 智能家居&#x…...

【算法训练营Day07】字符串part1
文章目录 反转字符串反转字符串II替换数字 反转字符串 题目链接:344. 反转字符串 双指针法,两个指针的元素直接调转即可 class Solution {public void reverseString(char[] s) {int head 0;int end s.length - 1;while(head < end) {char temp …...

CMake 从 GitHub 下载第三方库并使用
有时我们希望直接使用 GitHub 上的开源库,而不想手动下载、编译和安装。 可以利用 CMake 提供的 FetchContent 模块来实现自动下载、构建和链接第三方库。 FetchContent 命令官方文档✅ 示例代码 我们将以 fmt 这个流行的格式化库为例,演示如何: 使用 FetchContent 从 GitH…...

【OSG学习笔记】Day 16: 骨骼动画与蒙皮(osgAnimation)
骨骼动画基础 骨骼动画是 3D 计算机图形中常用的技术,它通过以下两个主要组件实现角色动画。 骨骼系统 (Skeleton):由层级结构的骨头组成,类似于人体骨骼蒙皮 (Mesh Skinning):将模型网格顶点绑定到骨骼上,使骨骼移动…...

微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据
微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据 Power Query 具有大量专门帮助您清理和准备数据以供分析的功能。 您将了解如何简化复杂模型、更改数据类型、重命名对象和透视数据。 您还将了解如何分析列,以便知晓哪些列包含有价值的数据,…...
提供了哪些便利?)
现有的 Redis 分布式锁库(如 Redisson)提供了哪些便利?
现有的 Redis 分布式锁库(如 Redisson)相比于开发者自己基于 Redis 命令(如 SETNX, EXPIRE, DEL)手动实现分布式锁,提供了巨大的便利性和健壮性。主要体现在以下几个方面: 原子性保证 (Atomicity)ÿ…...

ui框架-文件列表展示
ui框架-文件列表展示 介绍 UI框架的文件列表展示组件,可以展示文件夹,支持列表展示和图标展示模式。组件提供了丰富的功能和可配置选项,适用于文件管理、文件上传等场景。 功能特性 支持列表模式和网格模式的切换展示支持文件和文件夹的层…...

C# winform教程(二)----checkbox
一、作用 提供一个用户选择或者不选的状态,这是一个可以多选的控件。 二、属性 其实功能大差不差,除了特殊的几个外,与button基本相同,所有说几个独有的 checkbox属性 名称内容含义appearance控件外观可以变成按钮形状checkali…...

对象回调初步研究
_OBJECT_TYPE结构分析 在介绍什么是对象回调前,首先要熟悉下结构 以我们上篇线程回调介绍过的导出的PsProcessType 结构为例,用_OBJECT_TYPE这个结构来解析它,0x80处就是今天要介绍的回调链表,但是先不着急,先把目光…...

小智AI+MCP
什么是小智AI和MCP 如果还不清楚的先看往期文章 手搓小智AI聊天机器人 MCP 深度解析:AI 的USB接口 如何使用小智MCP 1.刷支持mcp的小智固件 2.下载官方MCP的示例代码 Github:https://github.com/78/mcp-calculator 安这个步骤执行 其中MCP_ENDPOI…...

游戏开发中常见的战斗数值英文缩写对照表
游戏开发中常见的战斗数值英文缩写对照表 基础属性(Basic Attributes) 缩写英文全称中文释义常见使用场景HPHit Points / Health Points生命值角色生存状态MPMana Points / Magic Points魔法值技能释放资源SPStamina Points体力值动作消耗资源APAction…...
