【算法分析与设计】最大二叉树

📝个人主页:五敷有你
🔥系列专栏:算法分析与设计
⛺️稳中求进,晒太阳

题目
给定一个不重复的整数数组
nums。 最大二叉树 可以用下面的算法从nums递归地构建:
- 创建一个根节点,其值为
nums中的最大值。- 递归地在最大值 左边 的 子数组前缀上 构建左子树。
- 递归地在最大值 右边 的 子数组后缀上 构建右子树。
返回
nums构建的 最大二叉树 。
示例
示例 1:
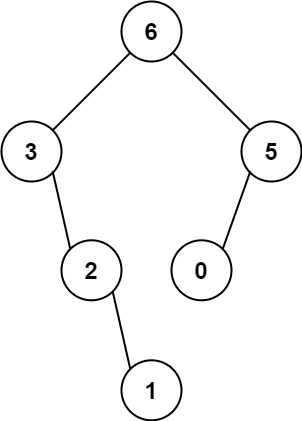
输入:nums = [3,2,1,6,0,5] 输出:[6,3,5,null,2,0,null,null,1] 解释:递归调用如下所示: - [3,2,1,6,0,5] 中的最大值是 6 ,左边部分是 [3,2,1] ,右边部分是 [0,5] 。- [3,2,1] 中的最大值是 3 ,左边部分是 [] ,右边部分是 [2,1] 。- 空数组,无子节点。- [2,1] 中的最大值是 2 ,左边部分是 [] ,右边部分是 [1] 。- 空数组,无子节点。- 只有一个元素,所以子节点是一个值为 1 的节点。- [0,5] 中的最大值是 5 ,左边部分是 [0] ,右边部分是 [] 。- 只有一个元素,所以子节点是一个值为 0 的节点。- 空数组,无子节点。
示例 2:
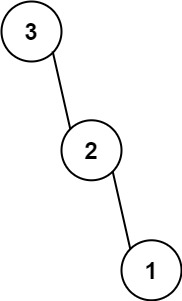
输入:nums = [3,2,1] 输出:[3,null,2,null,1]
思路
用递归实现,construct(int[] nums,int left,int right)。
表示对数组nums从nums[left]到nums[right] 的元素构建一棵树。我们首先找到这一区间中的最大值,记为nums[best].这样就确定了根节点的值。随后我们就可以进行递归:
左子树为 construct(nums,left,best−1);
右子树为 construct(nums,left,best−1)
当递归到一个无效的区间(即 left>right)时,便可以返回一棵空的树.
代码实现
/*** Definition for a binary tree node.* public class TreeNode {* int val;* TreeNode left;* TreeNode right;* TreeNode() {}* TreeNode(int val) { this.val = val; }* TreeNode(int val, TreeNode left, TreeNode right) {* this.val = val;* this.left = left;* this.right = right;* }* }*/
class Solution {public TreeNode constructMaximumBinaryTree(int[] nums) {return construct(nums,0,nums.length-1);}public TreeNode construct(int[] nums,int left,int right){if(left>right){return null;}int best=left;for(int i=left;i<=right;i++){best=nums[best]>nums[i]?best:i;}TreeNode node=new TreeNode();node.val=nums[best];node.left=func(nums,left,best-1);node.right=func(nums,best+1,right);return node;}
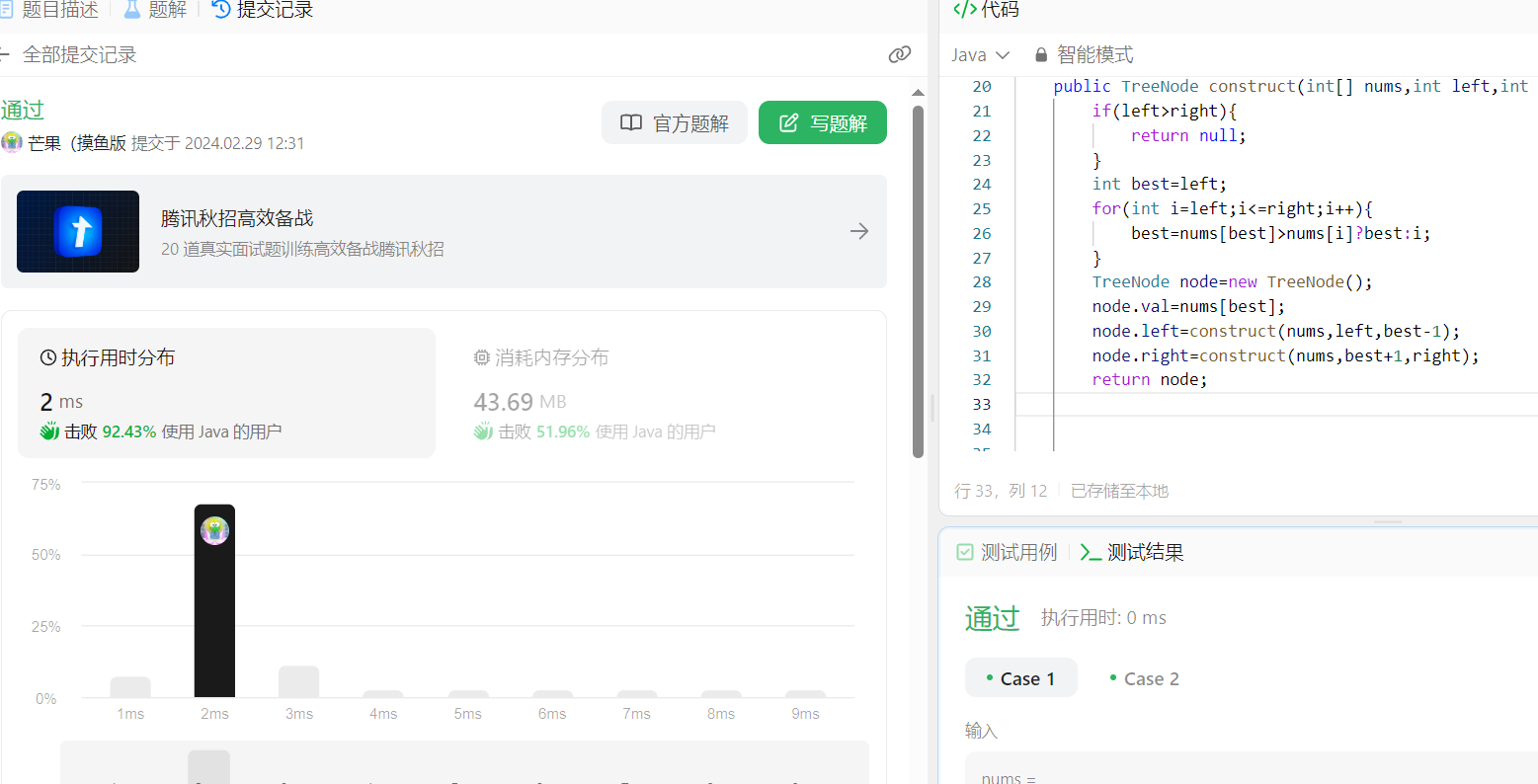
}运行结果
时间复杂度O(n^2)
空间复杂度O(n)
相关文章:

【算法分析与设计】最大二叉树
📝个人主页:五敷有你 🔥系列专栏:算法分析与设计 ⛺️稳中求进,晒太阳 题目 给定一个不重复的整数数组 nums 。 最大二叉树 可以用下面的算法从 nums 递归地构建: 创建一个根节点,其值为 nums 中的最…...
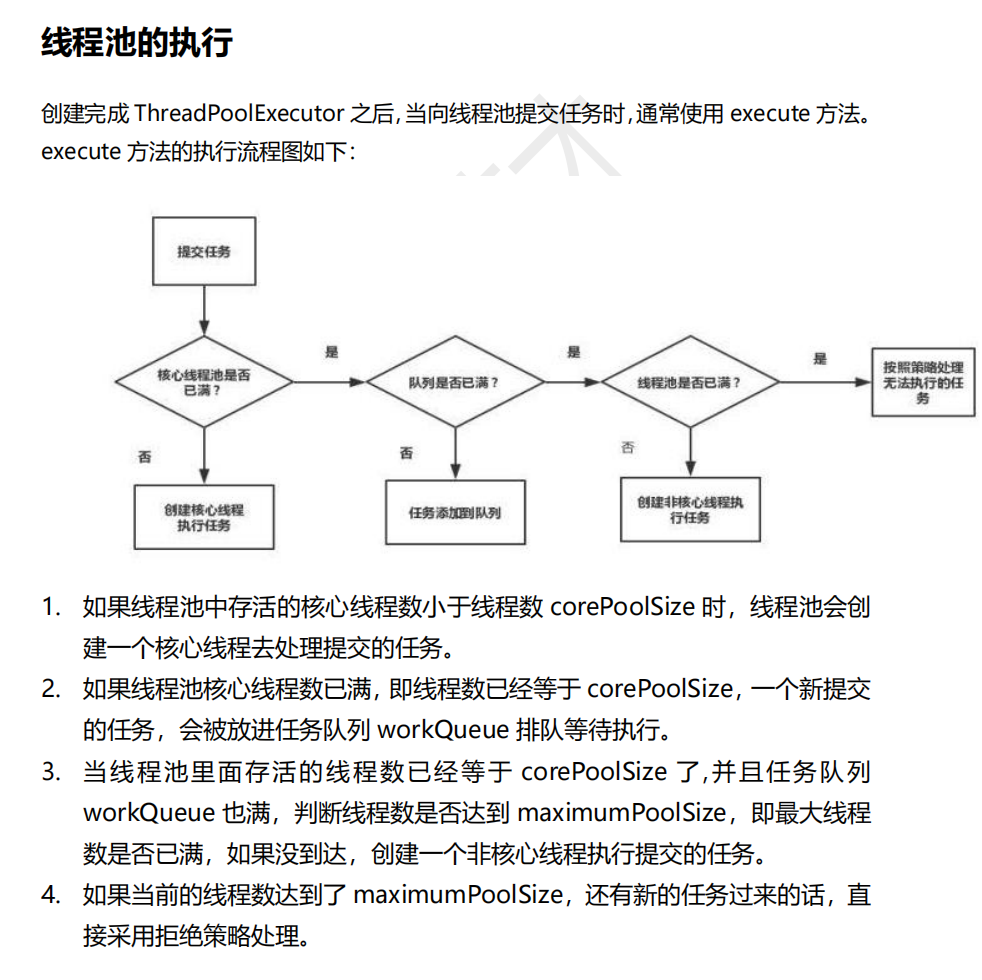
面试问答总结之并发编程
文章目录 🐒个人主页🏅JavaEE系列专栏📖前言:🎀多线程的优点、缺点🐕并发编程的核心问题 :不可见性、乱序性、非原子性🪀不可见性🪀乱序性🪀非原子性…...

红外测温仪芯片方案开发设计
红外测温仪由光学系统、光电探测器、信号放大器及信号处理、显示输出等部分组成。光学系统汇集其视场内的目标红外辐射能量,视场的大小由测温仪的光学零件以及位置决定。被测物体辐射的红外首先进入测温仪的光学系统,再由光学系统汇聚射入的红外线&#…...
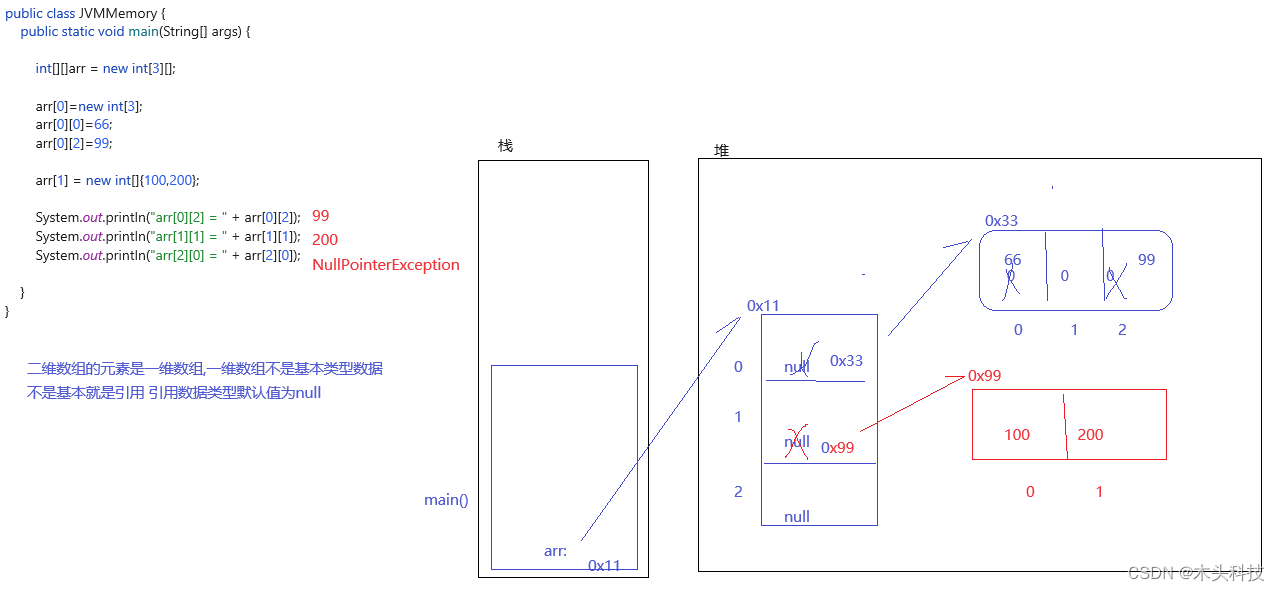
五、数组——Java基础篇
五、数组 1、数组元素的遍历 1.1数组的遍历:将数组内的元素展现出来 1、普通for遍历:根据下表获取数组内的元素 2、增强for遍历: for(数据元素类型 变量名:数组名){ 变量名:数组内的每一个值…...

如何用golang写一个自己的后端框架
如果你想要不使用任何现有的后端框架,完全从头开始创建一个后端框架,你需要实现Web服务器的基本组件,比如路由器、请求处理、中间件支持等。以下是一个简单的指南,用于创建一个基本的、不使用任何外部框架的Go后端框架。 步骤 1: 设置工作环境 确保你已经安装了Go语言环境…...

linux 如何给服务器批量做免密,如何批量挂在磁盘
前提条件 所有机器网络互通,且已做了免密登录 linux服务器批量做免密脚本如下 #!/bin/bash # 定义服务器列表文件 SERVERS_FILE"host" # 定义生成的密钥的存储目录 KEY_DIR"/root/.ssh" # 检查是否输入了文件路径 if [ $# -ne 1 ]; then …...

Android Activity的生命周期详解
在Android开发中,了解Activity的生命周期是非常重要的,它决定了Activity在不同状态下的行为和处理逻辑。Android中的Activity生命周期包括多个方法,每个方法都代表了Activity在特定状态下的行为。下面我们来逐一介绍这些方法及其对应的生命周…...

python学习笔记-内置类型
Python内置类型是Python编程语言中自带的基本数据类型,它们用于存储和处理数据。其中包括数字、序列、映射、类、实例和异常等主要类型。 在这些内置类型中,有一些是可变的,它们具有修改自身内容的能力,比如添加、移除或重排成员…...
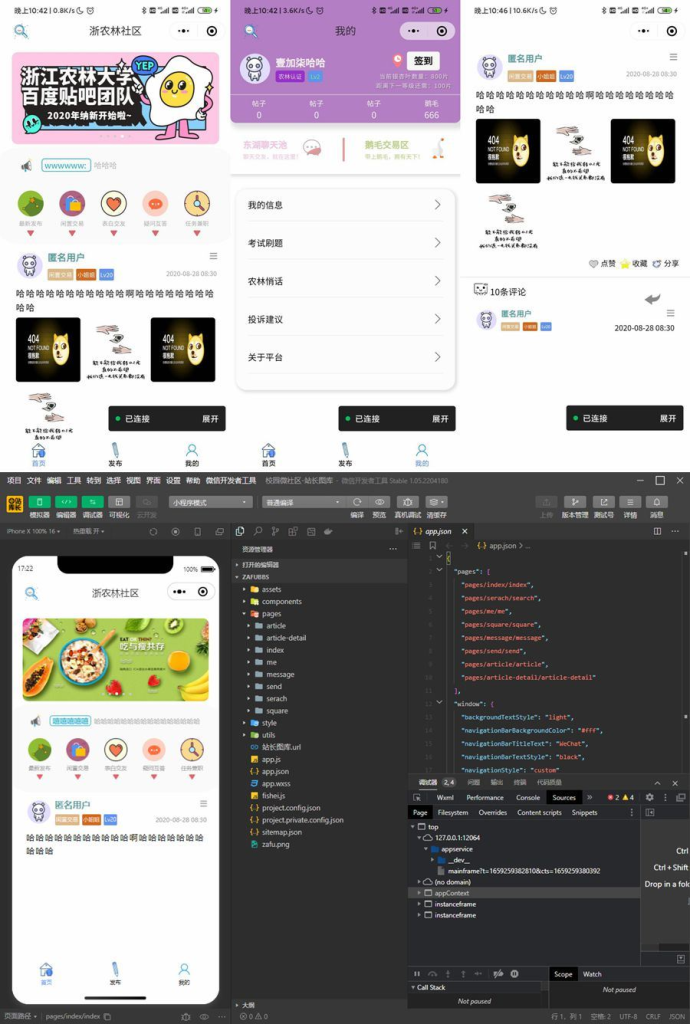
校园微社区微信小程序源码/二手交易/兼职交友微信小程序源码
云开发校园微社区微信小程序开源源码,这是一款云开发校园微社区-二手交易_兼职_交友_项目微信小程序开源源码,可以给你提供快捷方便的校园生活,有很多有趣实用的板块和功能,如:闲置交易、表白交友、疑问互答、任务兼职…...

如何在 Angular 中使用 NgTemplateOutlet 创建可重用组件
简介 单一职责原则是指应用程序的各个部分应该只有一个目的。遵循这个原则可以使您的 Angular 应用程序更容易测试和开发。 在 Angular 中,使用 NgTemplateOutlet 而不是创建特定组件,可以使组件在不修改组件本身的情况下轻松修改为各种用例。 在本文…...

改进的yolo交通标志tt100k数据集目标检测(代码+原理+毕设可用)
YOLO TT100K: 基于YOLO训练的交通标志检测模型 在原始代码基础上: 修改数据加载类,支持CoCo格式(使用cocoapi);修改数据增强;validation增加mAP计算;修改anchor; 注: 实验开启weig…...

nginx 日志,压缩,https功能介绍
一, 自定义访问日志 (一)日志位置存放 1,格式 2, 级别 level: debug, info, notice, warn, error, crit, alert, emerg 3,示例 服务机定义 错误日志存放位置 客户机错误访问 查看错误日志 4ÿ…...

代码随想录三刷day17
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 前言一、力扣144. 二叉树的前序遍历二、力扣145. 二叉树的后序遍历三、力扣94. 二叉树的中序遍历四、力扣144. 二叉树的前序遍历无、力扣145. 二叉树的后序遍历六、…...

postcss-px-to-viewport include属性
包含include配置的(github):npm i https://github.com/evrone/postcss-px-to-viewport -S 包含include配置的(npm):npm i postcss-px-to-viewport-8-with-include -S 不包含包include配置的(npm):npm i postcss-px-to-viewport 看了一下这篇文…...

C++设计模式——抽象工厂模式
文章目录 抽象工厂模式的主要组成部分抽象工厂模式的一个典型例子抽象工厂模式用于其他场景抽象工厂模式与其他设计模式结合使用 C 中的抽象工厂模式是一种创建型设计模式,它主要用于处理对象家族的创建,这些对象之间可能存在一定的关联关系或属于相同的…...
Windows安装VNC连接工具并结合cpolar实现远程内网Ubuntu系统桌面
文章目录 前言1. ubuntu安装VNC2. 设置vnc开机启动3. windows 安装VNC viewer连接工具4. 内网穿透4.1 安装cpolar【支持使用一键脚本命令安装】4.2 创建隧道映射4.3 测试公网远程访问 5. 配置固定TCP地址5.1 保留一个固定的公网TCP端口地址5.2 配置固定公网TCP端口地址5.3 测试…...

Vue3 Hooks函数使用及封装思想
一、什么是Hooks函数? 想象一下,你在做饭,有一些调料你经常会用到,比如盐、酱油和辣椒。每次做饭时,你都会从柜子里拿出这些调料。如果你每次用完都把它们随便放在厨房的某个角落,下次做饭时就可能找不到它…...

YOLOv8改进涨点,添加GSConv+Slim Neck,有效提升目标检测效果,代码改进(超详细)
目录 摘要 主要想法 GSConv GSConv代码实现 slim-neck slim-neck代码实现 yaml文件 完整代码分享 总结 摘要 目标检测是计算机视觉中重要的下游任务。对于车载边缘计算平台来说,巨大的模型很难达到实时检测的要求。而且,由大量深度可分离卷积层构…...
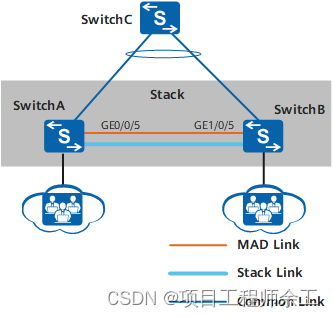
华为s5720s-28p-power-li-ac堆叠配置
叠物理约束: • 连线推荐示意图选用产品子系列中固定的一款设备做示例,与选择产品时指定型号的外观可能不同。示意图主要用于让用户了解相同子系列设备可以用作堆叠的端口的位置,以及使用不同的连线方式时如何连接设备上的端口。因此…...

c# aes加密解密私钥公钥通钥
using System.Security.Cryptography; using System.Text; namespace EncryptTest { internal class Program { static void Main(string[] args) { Console.WriteLine("Hello, World!"); string 密 EncryptAESBASE64("你…...

python打卡day49
知识点回顾: 通道注意力模块复习空间注意力模块CBAM的定义 作业:尝试对今天的模型检查参数数目,并用tensorboard查看训练过程 import torch import torch.nn as nn# 定义通道注意力 class ChannelAttention(nn.Module):def __init__(self,…...

golang循环变量捕获问题
在 Go 语言中,当在循环中启动协程(goroutine)时,如果在协程闭包中直接引用循环变量,可能会遇到一个常见的陷阱 - 循环变量捕获问题。让我详细解释一下: 问题背景 看这个代码片段: fo…...

8k长序列建模,蛋白质语言模型Prot42仅利用目标蛋白序列即可生成高亲和力结合剂
蛋白质结合剂(如抗体、抑制肽)在疾病诊断、成像分析及靶向药物递送等关键场景中发挥着不可替代的作用。传统上,高特异性蛋白质结合剂的开发高度依赖噬菌体展示、定向进化等实验技术,但这类方法普遍面临资源消耗巨大、研发周期冗长…...

ESP32 I2S音频总线学习笔记(四): INMP441采集音频并实时播放
简介 前面两期文章我们介绍了I2S的读取和写入,一个是通过INMP441麦克风模块采集音频,一个是通过PCM5102A模块播放音频,那如果我们将两者结合起来,将麦克风采集到的音频通过PCM5102A播放,是不是就可以做一个扩音器了呢…...

k8s业务程序联调工具-KtConnect
概述 原理 工具作用是建立了一个从本地到集群的单向VPN,根据VPN原理,打通两个内网必然需要借助一个公共中继节点,ktconnect工具巧妙的利用k8s原生的portforward能力,简化了建立连接的过程,apiserver间接起到了中继节…...

08. C#入门系列【类的基本概念】:开启编程世界的奇妙冒险
C#入门系列【类的基本概念】:开启编程世界的奇妙冒险 嘿,各位编程小白探险家!欢迎来到 C# 的奇幻大陆!今天咱们要深入探索这片大陆上至关重要的 “建筑”—— 类!别害怕,跟着我,保准让你轻松搞…...

【C++进阶篇】智能指针
C内存管理终极指南:智能指针从入门到源码剖析 一. 智能指针1.1 auto_ptr1.2 unique_ptr1.3 shared_ptr1.4 make_shared 二. 原理三. shared_ptr循环引用问题三. 线程安全问题四. 内存泄漏4.1 什么是内存泄漏4.2 危害4.3 避免内存泄漏 五. 最后 一. 智能指针 智能指…...

ubuntu22.04有线网络无法连接,图标也没了
今天突然无法有线网络无法连接任何设备,并且图标都没了 错误案例 往上一顿搜索,试了很多博客都不行,比如 Ubuntu22.04右上角网络图标消失 最后解决的办法 下载网卡驱动,重新安装 操作步骤 查看自己网卡的型号 lspci | gre…...
的打车小程序)
基于鸿蒙(HarmonyOS5)的打车小程序
1. 开发环境准备 安装DevEco Studio (鸿蒙官方IDE)配置HarmonyOS SDK申请开发者账号和必要的API密钥 2. 项目结构设计 ├── entry │ ├── src │ │ ├── main │ │ │ ├── ets │ │ │ │ ├── pages │ │ │ │ │ ├── H…...

基于单片机的宠物屋智能系统设计与实现(论文+源码)
本设计基于单片机的宠物屋智能系统核心是实现对宠物生活环境及状态的智能管理。系统以单片机为中枢,连接红外测温传感器,可实时精准捕捉宠物体温变化,以便及时发现健康异常;水位检测传感器时刻监测饮用水余量,防止宠物…...
