【深度优先搜索】【图论】【推荐】332. 重新安排行程
作者推荐
动态规划的时间复杂度优化
本文涉及知识点
深度优先搜索 图论
LeetCode332. 重新安排行程
给你一份航线列表 tickets ,其中 tickets[i] = [fromi, toi] 表示飞机出发和降落的机场地点。请你对该行程进行重新规划排序。
所有这些机票都属于一个从 JFK(肯尼迪国际机场)出发的先生,所以该行程必须从 JFK 开始。如果存在多种有效的行程,请你按字典排序返回最小的行程组合。
例如,行程 [“JFK”, “LGA”] 与 [“JFK”, “LGB”] 相比就更小,排序更靠前。
假定所有机票至少存在一种合理的行程。且所有的机票 必须都用一次 且 只能用一次。
示例 1:

输入:tickets = [[“MUC”,“LHR”],[“JFK”,“MUC”],[“SFO”,“SJC”],[“LHR”,“SFO”]]
输出:[“JFK”,“MUC”,“LHR”,“SFO”,“SJC”]
示例 2:

输入:tickets = [[“JFK”,“SFO”],[“JFK”,“ATL”],[“SFO”,“ATL”],[“ATL”,“JFK”],[“ATL”,“SFO”]]
输出:[“JFK”,“ATL”,“JFK”,“SFO”,“ATL”,“SFO”]
解释:另一种有效的行程是 [“JFK”,“SFO”,“ATL”,“JFK”,“ATL”,“SFO”] ,但是它字典排序更大更靠后。
提示:
1 <= tickets.length <= 300
tickets[i].length == 2
fromi.length == 3
toi.length == 3
fromi 和 toi 由大写英文字母组成
fromi != toi
基础知识
定义
如果图G中的一个路径包括每个边恰好一次,则该路径称为欧拉路径(Euler path)。
如果一个回路是欧拉路径,则称为欧拉回路(Euler circuit)。
性质
性质一:一个有向图是欧拉回路 ⟺ \iff ⟺所有顶点的入度等于出度且该图是连通图。
性质二:一个有向图是欧拉路径 ⟺ \iff ⟺ 起点出度等于入度+1,终点入度=出度+1,其它顶点的入度等于出度且该图是连通图。
欧拉路径和回路符合性质比较简单,不证明。下面只证明性质一必定是欧拉回路,性质二是欧拉路径。
证明一
设有向图G符合性质一。
操作一:以任意定点为起点s,选取s的任意临接点n1,删除sn1后,除s外,其它顶点都是出度等于入度,就是进入后,一定会离开。由于顶点的出度和入度是有限的,所以一定会结束,而结束点一定是s(因为只有它入度大于出度)。设删除经过的路径为P1。
最后一次经过s后,可能有些点入度并不为0。
→ { ∗ ∗ 操作二 ∗ ∗ 图 G 删除 P 1 各边,此时余下的边 P 2 仍然符合性质一。 P 1 经过的各点,一定有点 n 2 出度不为 0 。否则与连通图矛盾。 \rightarrow\begin{cases}**操作二**图G删除P1各边,此时余下的边P2仍然符合性质一。\\ P1经过的各点,一定有点n2出度不为0。否则与连通图矛盾。\\ \end{cases} →{∗∗操作二∗∗图G删除P1各边,此时余下的边P2仍然符合性质一。P1经过的各点,一定有点n2出度不为0。否则与连通图矛盾。
操作二时:如果有重边,经过几次则删除几条。
以n2为起点对P2进行操作一,得到P3,必定以n2开始和结尾。
用P3替换P1的n2节点。如此往复直到所有节点出度入度为0。
证明二
设有向图G符合性质二,s出度=入度+1,e入度=出度+1。一定存在以s为起点,e为终点的路径P1。选取方法类似证明一,多个出边任选一条出边。图G删除P1后,为P2;P2要么为空,要么符合性质二。
深度优先搜索
题目确保某条从JFK为起点的路径是欧拉路径。
如果是欧拉环路:所有点出度等于入度。
如果不是环路:起点出度-1==入度 终点入度=出度+1,其它节点入度等于出度。
必须确保起点最后访问终点那一支,其它访问顺序按字典需。
DFS 函数

主函数
DFS(“JFK”)
颠倒m_vRes的顺序
返回m_vRet。
示例和时序图


按时间线访问m_vRes的顺序:DAFEACBA。转置(颠倒顺序)后为:ABCAEFAD。
证明:
假定图G的欧拉路径最后一个出度大于1的节点为c,它共有m+1+n条出边,按邻接字典序排序后,第m+1条出边指向终点e。
步骤一:只讨论节点c及之后的路径。设c的临接点按字典序分别为:n[1] …n[m+n+1]。
除DFS(n[1+m] → \rightarrow →e)可以直接结束,其它节点都必须等所有A的出边都访问结束(包括n[1+m]),所以 n[1+m] → \rightarrow →e 的逆序最先加到vRet。
c → \rightarrow →n[n+m+1]是c最后一条出边,故将 n[i+m+1] → \rightarrow →c 的逆序放到vRet 中。
c → \rightarrow →n[n+m ]是c最倒数第二条出边,故将 n[i+m] → \rightarrow →c 的逆序放到vRet 中。
⋯ \cdots ⋯ 将 n[1+m+1] → \rightarrow →c 的逆序放到vRet 中。
⋮ \vdots ⋮
⋯ \cdots ⋯ 将 n[m] → \rightarrow →c 的逆序放到vRet 中。
⋯ \cdots ⋯ n[1 ] → \rightarrow →c 的逆序放到vRet 中。
将c 放到vRet 中。
步骤二:将图G 节点c及之后节点的出边都删除。c变成新的终点。
不断持续步骤一二到所有节点的出度为1。注意:c等于e也符合。
代码
核心代码
class Solution {
public:vector<string> findItinerary(vector<vector<string>>& tickets) {std::unordered_map<string, multiset<string>> mNeiBo;for (const auto& v : tickets){mNeiBo[v[0]].emplace(v[1]);}DFS(mNeiBo, "JFK");std::reverse(m_vRet.begin(), m_vRet.end());return m_vRet;}void DFS(std::unordered_map<string, multiset<string>>& mNeiBo,const string& cur){while (mNeiBo[cur].size()){auto next = *mNeiBo[cur].begin();mNeiBo[cur].erase(mNeiBo[cur].begin());DFS(mNeiBo, next);}m_vRet.emplace_back(cur);}vector<string> m_vRet;
};
测试用例
template<class T,class T2>
void Assert(const T& t1, const T2& t2)
{assert(t1 == t2);
}template<class T>
void Assert(const vector<T>& v1, const vector<T>& v2)
{if (v1.size() != v2.size()){assert(false);return;}for (int i = 0; i < v1.size(); i++){Assert(v1[i], v2[i]);}}int main()
{vector<vector<string>> tickets;{Solution sln;tickets = { {"MUC","LHR"},{"JFK","MUC"},{"SFO","SJC"},{"LHR","SFO"} };auto res = sln.findItinerary(tickets);Assert({ "JFK","MUC","LHR","SFO","SJC" }, res);}{Solution sln;tickets = { {"JFK","SFO"},{"JFK","ATL"},{"SFO","ATL"},{"ATL","JFK"},{"ATL","SFO"} };auto res = sln.findItinerary(tickets);Assert({ "JFK","ATL","JFK","SFO","ATL","SFO" }, res);}
}
2023年4月
class Solution {
public:vector<string> findItinerary(vector<vector<string>>& tickets) { for (const auto& v : tickets){m_vNeiB[v[0]].emplace(v[1]);}dfs("JFK");std::reverse(m_vRet.begin(), m_vRet.end());return m_vRet;}void dfs(const string& sCur){while (m_vNeiB.count(sCur) && m_vNeiB[sCur].size()){const string sNext = m_vNeiB[sCur].top();m_vNeiB[sCur].pop();dfs(sNext);}m_vRet.emplace_back(sCur);}std::unordered_map < string, std::priority_queue<string, vector<string>, greater<string>>> m_vNeiB;vector<string> m_vRet;
};

扩展阅读
视频课程
有效学习:明确的目标 及时的反馈 拉伸区(难度合适),可以先学简单的课程,请移步CSDN学院,听白银讲师(也就是鄙人)的讲解。
https://edu.csdn.net/course/detail/38771
如何你想快
速形成战斗了,为老板分忧,请学习C#入职培训、C++入职培训等课程
https://edu.csdn.net/lecturer/6176
相关
下载
想高屋建瓴的学习算法,请下载《喜缺全书算法册》doc版
https://download.csdn.net/download/he_zhidan/88348653
| 我想对大家说的话 |
|---|
| 闻缺陷则喜是一个美好的愿望,早发现问题,早修改问题,给老板节约钱。 |
| 子墨子言之:事无终始,无务多业。也就是我们常说的专业的人做专业的事。 |
| 如果程序是一条龙,那算法就是他的是睛 |
测试环境
操作系统:win7 开发环境: VS2019 C++17
或者 操作系统:win10 开发环境: VS2022 C++17
如无特殊说明,本算法用**C++**实现。

相关文章:

【深度优先搜索】【图论】【推荐】332. 重新安排行程
作者推荐 动态规划的时间复杂度优化 本文涉及知识点 深度优先搜索 图论 LeetCode332. 重新安排行程 给你一份航线列表 tickets ,其中 tickets[i] [fromi, toi] 表示飞机出发和降落的机场地点。请你对该行程进行重新规划排序。 所有这些机票都属于一个从 JFK&a…...
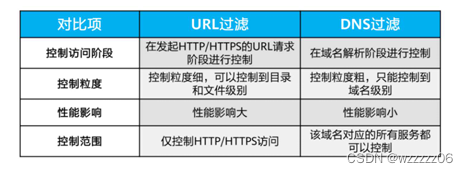
DAY9-防病毒AV概述
DNS过滤 URL过滤和DNS过滤对比...

TCP缓存
TCP缓存是指TCP协议在数据传输过程中使用的一种机制,用于临时存储和管理数据包。它主要有三个作用:提高网络性能、保证数据的可靠性和实现流量控制。 首先,TCP缓存可以提高网络性能。当发送端发送数据时,TCP协议会将数据分割成若…...
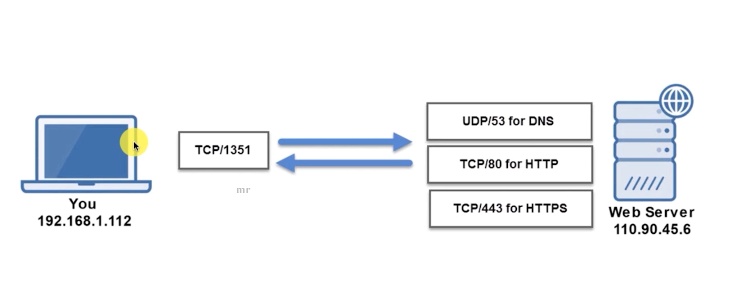
Socket网络编程(一)——网络通信入门基本概念
目录 网络通信基本概念什么是网络?网络通信的基本架构什么是网络编程?7层网络模型-OSI模型什么是Socket?Socket的作用和组成Socket传输原理Socket与TCP、UDP的关系CS模型(Client-Server Application)报文段牛刀小试(TCP消息发送与接收&#…...
)
RTCA DO-178C 机载系统和设备认证中的软件注意事项-软件质量保证流程(八)
8.0 软件质量保证流程 SOFTWARE QUALITY ASSURANCE PROCESS 本节讨论软件质量保证 (SQA) 过程的目标和活动。 SQA 流程按照软件规划流程(参见 4)和软件质量保证计划(参见 11.5)的定义进行应用。 SQA 过程活动的输出记录在软件质量…...
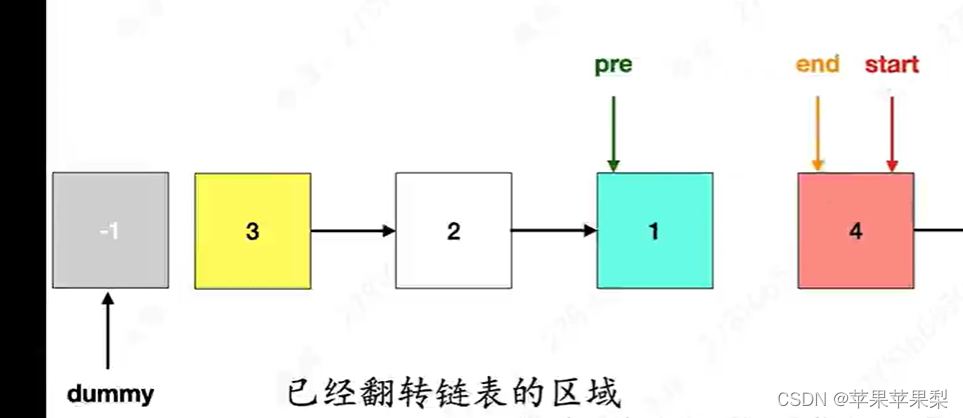
K 个一组翻转链表 力扣
【玩转校招算法面试】第三天:链表中的节点每k个一组翻转(动画演示、手写 Java 代码、详细注释、LeetCode 高频算法题)_哔哩哔哩_bilibili 初始状态:1 -> 2 -> 3,pre null, cur 1保存当前节点的下一个节点&…...

Java毕业设计 基于SSM SpringBoot vue购物比价网站
Java毕业设计 基于SSM SpringBoot vue购物比价网站 SSM vue 购物比价网站 功能介绍 首页 图片轮播 商品 商品分类 商品详情 评论 收藏 商品攻略 商品信息 公告栏 在线反馈 登录 注册 个人中心 我的收藏 后台管理 登录 注册商品户 个人中心 修改密码 个人信息 商品户管理 用户…...

Linux按键输入实验-按键功能完善
一. 简介 前面一篇文章实现了 按键的字符设备驱动代码框架,文章地址如下: Linux按键输入实验-按键的字符设备驱动代码框架-CSDN博客 本文在 字符设备驱动框架实现的基础上,加入按键GPIO的初始化功能。 二. Linux按键输入实验-按键的GPIO…...
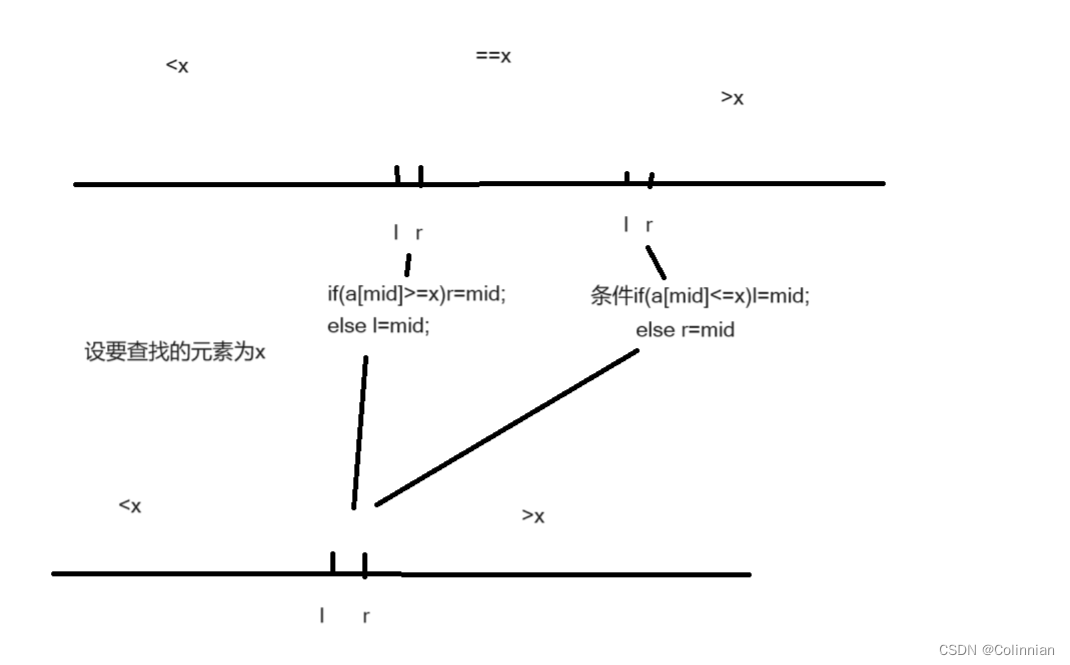
二分查找讲解
关于我为什么要写单独开一篇文章写二分,实际上那么多困难的算法,比如线段树,并查集等等都没有难倒我,我最近却被二分难倒了,而且是两次,两次在赛场上做不出来二分的应用题,于是我决定写一篇二分查找的算法总结.刚接触算法的时候本来是要写一篇的,但后面因为各种原因搁置了,现在…...

跨区域复制建筑UI输入框脚本迷你世界
--复制区域文件 --设置坐标起点,终点 --创建区域 --获取坐标id,data --星空露珠工作室制作 local pos1{x-16,y7,z28} local pos2{x28,y44,z-9} local block{num0} local str{} local str0{} local num0 local count0 local ui6 --几个输入框 local romath.random(…...

取消退出流程控制方法
在自动化设备动作流程中,人为任意想取消当前动作,常见方法是使用全局变量,实时检测变量决定退出。这里介绍一个System.Threading空间下的 CancellationTokenSource类,他可以设置超时,设置信息等封装 基本使用超时和手…...

力扣-跳跃游戏
问题 给你一个非负整数数组 nums ,你最初位于数组的 第一个下标 。数组中的每个元素代表你在该位置可以跳跃的最大长度。 判断你是否能够到达最后一个下标,如果可以,返回 true ;否则,返回 false 。 解答 class Solu…...
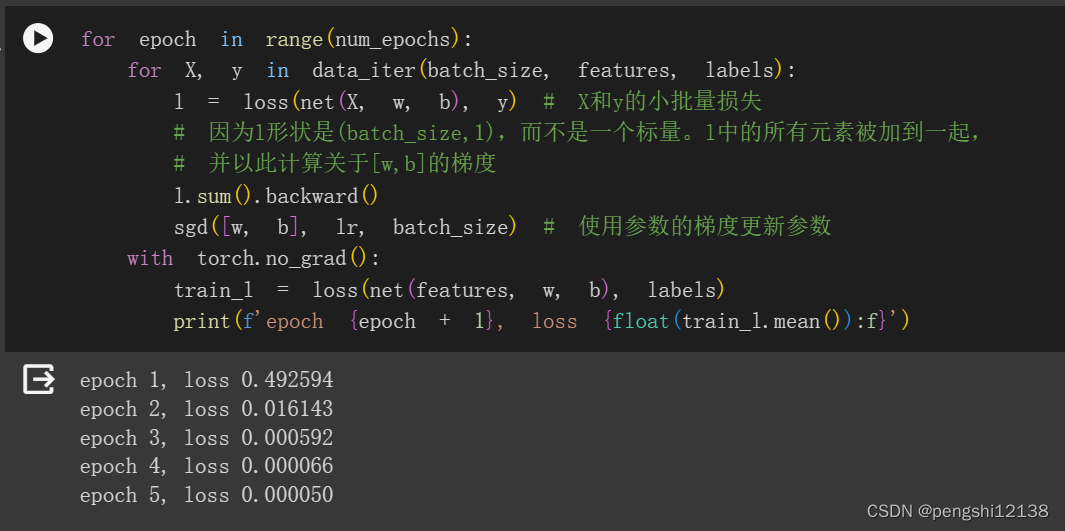
李沐动手学习深度学习——3.2练习
以下是个人理解,希望进行讨论求解。 练习 1. 如果我们将权重初始化为零,会发生什么。算法仍然有效吗? 根据SGD算法公式如上,第一次迭代的值可知w只与b相关,而对于b的迭代更新,只是与b的初始值相关&#x…...

代码随想录Day20 | Leetcode77 组合
题目 给定两个整数 n 和 k,返回范围 [1, n] 中所有可能的 k 个数的组合。你可以按 任何顺序 返回答案。示例 1: 输入:n 4, k 2 输出: [[2,4],[3,4],[2,3],[1,2],[1,3],[1,4], ]示例 2: 输入:n 1, k 1 …...
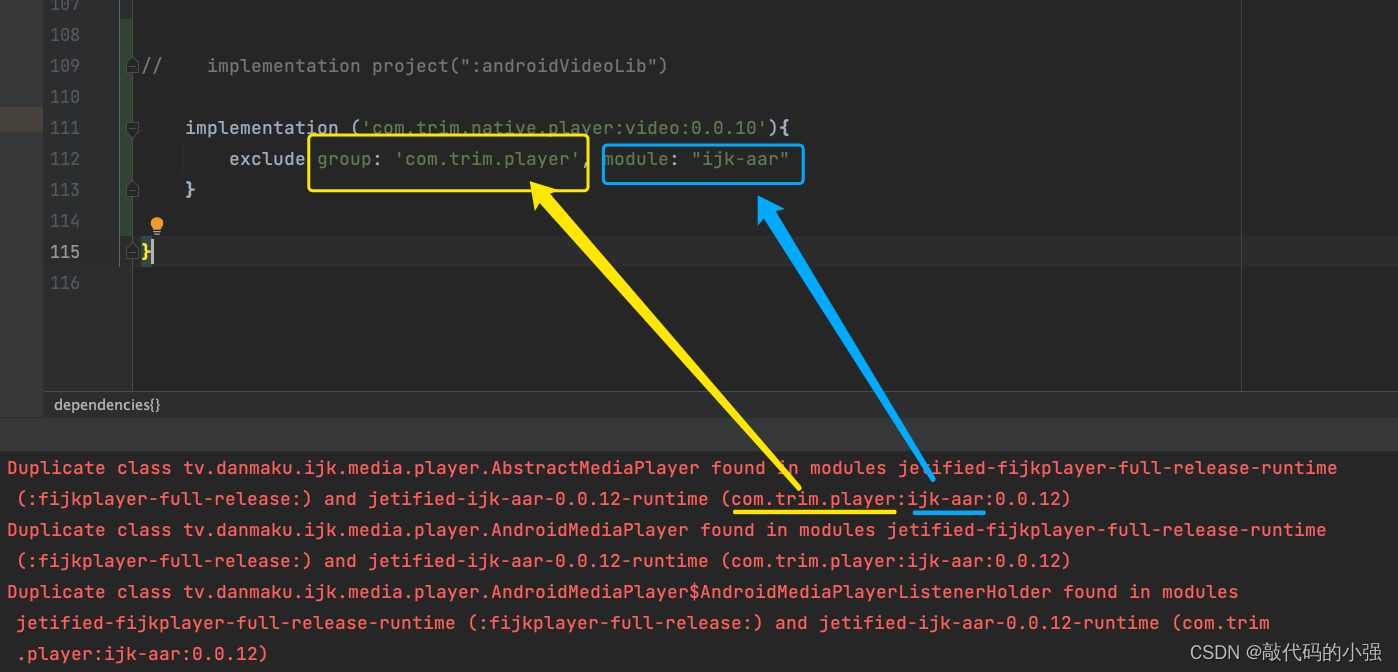
Android Duplicate class 排除重复类
一、起因: 在迭代开发的时候,发现2个ijk很多类重复。但又2个库实现的功能是不一样,目前不能合并。但又想保留2个功能。需要排除其中一个库。 二、报错如何下图: 三、解决方法: 3.1 在terminal 也就是命令行处输入 …...
是什么?有什么用?有哪些类型?)
【Kubernetes】服务(Service)是什么?有什么用?有哪些类型?
系列文章目录 K8s中的Namespace是什么? Kubernetes 集群的组件介绍 Kubernetes 对象是什么? Pod——k8s中最重要的对象之一 Kubernetes 和 Docker 之间有什么区别? 部署安装 K8s 为什么要关闭 swap 分区? k8s中容器之间、pod之间…...
【前端素材】推荐优质后台管理系统DAdmin平台模板(附源码)
一、需求分析 1、系统定义 后台管理系统是一种用于管理网站、应用程序或系统的管理界面,通常由管理员和工作人员使用。它提供了访问和控制网站或应用程序后台功能的工具和界面,使其能够管理用户、内容、数据和其他各种功能。 2、功能需求 后台管理系…...

Redis高级特性详解:事务处理、发布订阅、持久化和集群
Redis(Remote Dictionary Server)是一个开源的基于内存的数据结构存储系统,被广泛应用于缓存、队列、计数器等场景中。除了基本的键值存储功能外,Redis还提供了许多高级特性,包括事务处理、发布订阅、持久化和集群。在…...

nwjs做自动化测试
分别是2个常用的自动化测试化框架 GitHub - nwutils/nw-selenium-javascript-example: An example of end-to-end testing with Selenium for NW.js apps via JavaScript GitHub - nwutils/nw-puppeteer-example: An example of using NW.js via Puppeteer. 看习惯使用哪个&…...
【前端素材】推荐优质在线特殊品牌商城电商网页eStore平台模板(附源码)
一、需求分析 1、系统定义 在线特殊品牌商城是指一个通过互联网提供特定品牌或特殊类型商品购买服务的电子商务平台。这类商城专注于某个特定品牌、设计风格或商品类型,为顾客提供独特、专业的购物体验。 2、功能需求 在线特殊品牌商城是指一个通过互联网提供特…...

模型参数、模型存储精度、参数与显存
模型参数量衡量单位 M:百万(Million) B:十亿(Billion) 1 B 1000 M 1B 1000M 1B1000M 参数存储精度 模型参数是固定的,但是一个参数所表示多少字节不一定,需要看这个参数以什么…...

python/java环境配置
环境变量放一起 python: 1.首先下载Python Python下载地址:Download Python | Python.org downloads ---windows -- 64 2.安装Python 下面两个,然后自定义,全选 可以把前4个选上 3.环境配置 1)搜高级系统设置 2…...

蓝桥杯 2024 15届国赛 A组 儿童节快乐
P10576 [蓝桥杯 2024 国 A] 儿童节快乐 题目描述 五彩斑斓的气球在蓝天下悠然飘荡,轻快的音乐在耳边持续回荡,小朋友们手牵着手一同畅快欢笑。在这样一片安乐祥和的氛围下,六一来了。 今天是六一儿童节,小蓝老师为了让大家在节…...

如何为服务器生成TLS证书
TLS(Transport Layer Security)证书是确保网络通信安全的重要手段,它通过加密技术保护传输的数据不被窃听和篡改。在服务器上配置TLS证书,可以使用户通过HTTPS协议安全地访问您的网站。本文将详细介绍如何在服务器上生成一个TLS证…...

WordPress插件:AI多语言写作与智能配图、免费AI模型、SEO文章生成
厌倦手动写WordPress文章?AI自动生成,效率提升10倍! 支持多语言、自动配图、定时发布,让内容创作更轻松! AI内容生成 → 不想每天写文章?AI一键生成高质量内容!多语言支持 → 跨境电商必备&am…...
)
WEB3全栈开发——面试专业技能点P2智能合约开发(Solidity)
一、Solidity合约开发 下面是 Solidity 合约开发 的概念、代码示例及讲解,适合用作学习或写简历项目背景说明。 🧠 一、概念简介:Solidity 合约开发 Solidity 是一种专门为 以太坊(Ethereum)平台编写智能合约的高级编…...

深入解析C++中的extern关键字:跨文件共享变量与函数的终极指南
🚀 C extern 关键字深度解析:跨文件编程的终极指南 📅 更新时间:2025年6月5日 🏷️ 标签:C | extern关键字 | 多文件编程 | 链接与声明 | 现代C 文章目录 前言🔥一、extern 是什么?&…...

pikachu靶场通关笔记22-1 SQL注入05-1-insert注入(报错法)
目录 一、SQL注入 二、insert注入 三、报错型注入 四、updatexml函数 五、源码审计 六、insert渗透实战 1、渗透准备 2、获取数据库名database 3、获取表名table 4、获取列名column 5、获取字段 本系列为通过《pikachu靶场通关笔记》的SQL注入关卡(共10关࿰…...

Maven 概述、安装、配置、仓库、私服详解
目录 1、Maven 概述 1.1 Maven 的定义 1.2 Maven 解决的问题 1.3 Maven 的核心特性与优势 2、Maven 安装 2.1 下载 Maven 2.2 安装配置 Maven 2.3 测试安装 2.4 修改 Maven 本地仓库的默认路径 3、Maven 配置 3.1 配置本地仓库 3.2 配置 JDK 3.3 IDEA 配置本地 Ma…...
相比,优缺点是什么?适用于哪些场景?)
Redis的发布订阅模式与专业的 MQ(如 Kafka, RabbitMQ)相比,优缺点是什么?适用于哪些场景?
Redis 的发布订阅(Pub/Sub)模式与专业的 MQ(Message Queue)如 Kafka、RabbitMQ 进行比较,核心的权衡点在于:简单与速度 vs. 可靠与功能。 下面我们详细展开对比。 Redis Pub/Sub 的核心特点 它是一个发后…...
