Acwing-基础算法课笔记之数学知识(扩展欧几里得算法)
Acwing-基础算法课笔记之数学知识(扩展欧几里得算法)
- 一、扩展欧几里得算法
- 1、裴蜀定理
- 2、过程模拟
- 3、代码模板
- 二、线性同余方程
- 1、定义
- 2、模拟过程
- 3、结论证明
一、扩展欧几里得算法
1、裴蜀定理
对于任意正整数 a a a, b b b,那么一定存在非零整数 x x x, y y y,使得 a x + b y = e x g c d ( a , b ) ax+by=exgcd(a,b) ax+by=exgcd(a,b)
2、过程模拟
例如求 g c d ( a , b ) gcd(a,b) gcd(a,b)
∙ \bullet ∙当 b = 0 b=0 b=0 时,则可以直接返回 a a a 的值,即最大公约数,推理如下:
根据公式 a x + b y = e x g c d ( a , b ) ax+by=exgcd(a,b) ax+by=exgcd(a,b),得:
a × x + 0 × y = a a\times x+0\times y=a a×x+0×y=a
⇔ a × x = a \Lrarr a\times x=a ⇔a×x=a
⇔ x = 1 \Lrarr x=1 ⇔x=1
⇒ y = 0 \Rarr y=0 ⇒y=0
∙ \bullet ∙当 b ≠ 0 b\not =0 b=0 时,求得扩展欧几里得算法 e x g c d ( b , a % b , y , x ) exgcd(b,a\%b,y,x) exgcd(b,a%b,y,x),推理如下:
b y + ( a by+(a by+(a m o d mod mod b ) x = e x g c d ( a , b ) b)x=exgcd(a,b) b)x=exgcd(a,b)
⇒ a \rArr a ⇒a m o d mod mod b = a − ⌊ a b ⌋ b b=a-⌊\frac{a}{b}⌋b b=a−⌊ba⌋b
⇒ b y + ( a − ⌊ a b ⌋ b ) x = e x g c d ( a , b ) \rArr by+(a-⌊\frac{a}{b}⌋b)x=exgcd(a,b) ⇒by+(a−⌊ba⌋b)x=exgcd(a,b)
⇒ a x + b ( y − ⌊ a b ⌋ x ) = e x g c d ( a , b ) \rArr ax+b(y-⌊\frac{a}{b}⌋x)=exgcd(a,b) ⇒ax+b(y−⌊ba⌋x)=exgcd(a,b)
3、代码模板
// 求x, y,使得ax + by = gcd(a, b)
int exgcd(int a, int b, int &x, int &y)
{if (!b){x = 1; y = 0;return a;}int d = exgcd(b, a % b, y, x);y -= (a/b) * x;return d;
}
Acwing-扩展欧几里得算法
二、线性同余方程
1、定义
给定 n n n 组数据 a i a_i ai, b i b_i bi, m i m_i mi,对于每组数求出一个 x i x_i xi,使其满足 a i × x i ≡ b i ( m o d a_i\times x_i\equiv b_i(mod ai×xi≡bi(mod m i ) m_i) mi)。
2、模拟过程
设 a = 2 a=2 a=2, b = 3 b=3 b=3, m = 6 m=6 m=6,此时以上并不满足条件。
设 a = 4 a=4 a=4, b = 3 b=3 b=3, m = 5 m=5 m=5,要使 4 x % 5 = 3 4x\%5=3 4x%5=3,所以 x = − 3 x=-3 x=−3或 x = 2 x=2 x=2
3、结论证明
a × x ≡ b ( m o d a\times x\equiv b(mod a×x≡b(mod m ) m) m)
⇔ \Lrarr ⇔ ∃ y ∈ Z \exist y\in Z ∃y∈Z,使得 a x = m y + b ax=my+b ax=my+b
⇔ a x − m y = b \Lrarr ax-my=b ⇔ax−my=b
⇔ y ′ = − y \Lrarr y'=-y ⇔y′=−y
⇔ a x + m y ′ = g c d ( a , m ) \Lrarr ax+my'=gcd(a,m) ⇔ax+my′=gcd(a,m)(条件: g c d ( a , m ) ∣ b gcd(a,m)|b gcd(a,m)∣b)
相关文章:
)
Acwing-基础算法课笔记之数学知识(扩展欧几里得算法)
Acwing-基础算法课笔记之数学知识(扩展欧几里得算法) 一、扩展欧几里得算法1、裴蜀定理2、过程模拟3、代码模板 二、线性同余方程1、定义2、模拟过程3、结论证明 一、扩展欧几里得算法 1、裴蜀定理 对于任意正整数 a a a, b b b࿰…...
)
简单排列组合题(python版)
文章预览: 题目解法一输出结果 解法二输出结果输出结果 题目 有四个数字:1,2,3,4能组成多少个互不相同且无重复的数字的三位数? 各式多少? 解法一 我们粗略看一下这个题既然我们要组成三位数,那我们就循环3层每一层出一个数,并且if语句判…...

【排坑】搭建 Karmada 环境
git clone 报错 问题:Failed to connect to github.com port 443:connection timed out 解决: git config --global --unset http.proxy【hack/local-up-karmada.sh】 1. karmada ca-certificates (no such package) 问题:fetching http…...

每日一类:Qt GUI开发的基石《QWidget》
深入探索QWidget:Qt GUI开发的基石 在Qt框架中,QWidget类扮演着构建图形用户界面(GUI)的基础角色。它不仅提供了窗口的基本功能,还允许开发者通过继承和定制来创建各式各样的用户界面元素。本文将详细介绍QWidget的关…...
人大金仓与mysql的差异与替换
人大金仓中不能使用~下面的符号,字段中使用”,无法识别建表语句 创建表时语句中只定义字段名.字段类型.是否是否为空 Varchar类型改为varchar(长度 char) Int(0) 类型为int4 定义主键:CONSTRAINT 键名 主键类型&#x…...
Excel2LaTeX插件的使用、LaTeX表格
目录 一、下载Excel2Latex 二、使用Excel2Latex 1、将Excel2LaTeX文件添加到加载项 2、导出LaTex的表格数据 3、注意事项 1)生成的latex表格断断续续问题 2)改变线形的粗细 3)表格太大,需要缩小到适应大小 4)…...

MySQL 用了哪种默认隔离级别,实现原理是什么?
MySQL 的默认隔离级别是 RR - 可重复读,可以通过命令来查看 MySQL 中的默认隔离级别。 RR - 可重复读是基于多版本并发控制(Multi-Version Concurrency Control,MVCC )实现的。MVCC,在读取数据时通过一种类似快照的方…...
【C++初阶】第四站:类和对象(下)(理解+详解)
前言: 本篇知识点:初始化列表、explicit关键字、static成员、友元、内部类、匿名对象、编译器的优化 专栏:C初阶 目录 再谈构造函数 1️⃣构造函数体赋值 2️⃣初始化列表 explicit关键字 static成员 1.static概念 2.static特性 面试…...

redis的基本数据类型(一)
redis的基本数据类型 1、redis1.1、数据库分类1.2、NoSQL分类1.3、redis简介1.4、redis应用1.5、如何学习redis 2、redis的安装2.1、Windows安装2.2.1、客户端redis管理工具 2.2、Linux安装🔥2.2.1、redis核心文件2.2.2、启动方式2.2.3、redis桌面客户端1、redis命令…...
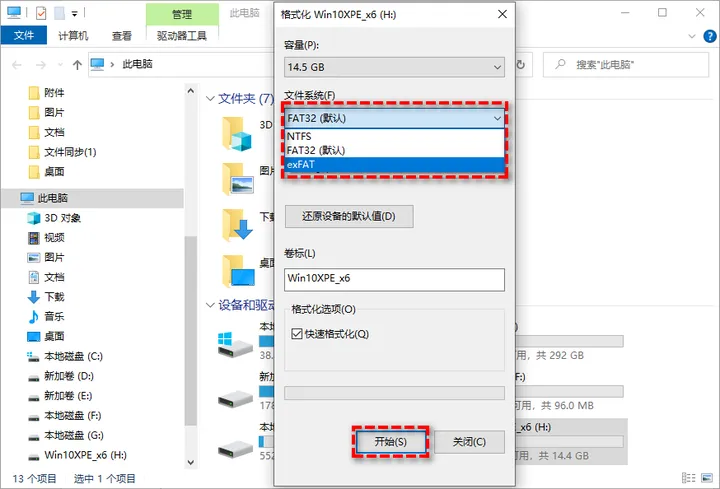
Windows无法识别exFAT格式怎么办?
Windows通常无法读取Mac格式的驱动器。如果使用Apple的HFS Plus将驱动器格式化为exFAT,默认情况下Windows无法读取exFAT驱动器,即使exFAT文件系统与Mac和Windows兼容。事实上,一些制造商销售的“Mac驱动器”是用这种限于Mac的文件系统预先格式…...

AI大模型的发展趋势?
大模型的发展趋势主要体现在以下几个方面: 1、模型规模的增长: 随着数据量和计算能力的不断增加,大型模型的规模也在不断扩大。模型参数数量、层数等指标不断刷新,以应对更复杂的任务和更大规模的数据。 2、多模态融合ÿ…...

List去除重复数据的五种方式
1、使用 LinkedHashSet 删除 arraylist 中的重复数据 LinkedHashSet 是在一个 ArrayList 删除重复数据的最佳方法。LinkedHashSet 在内部完成两件事: 删除重复数据 保持添加到其中的数据的顺序 Java 示例使用 LinkedHashSet 删除 arraylist 中的重复项。在给定的示例…...
VUE3自定义文章排行榜的简单界面
文章目录 一、代码展示二、代码解读三、结果展示 一、代码展示 <template><div class"article-ranking"><div class"header"><h2 class"title">{{ title }}</h2></div><div class"ranking-list&qu…...
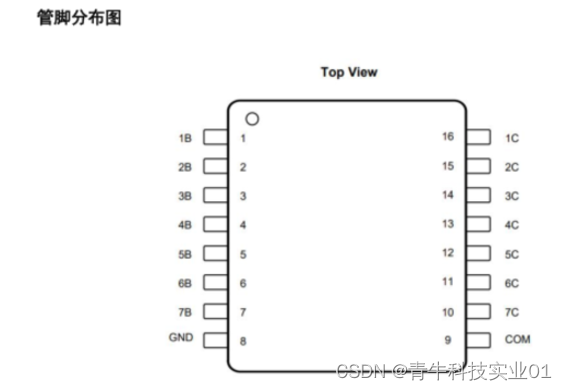
七通道NPN 达林顿管GC2003,专为符合标准 TTL 而制造,最高工作电压 50V,耐压 80V
GC2003 内部集成了 7 个 NPN 达林顿晶体管,连接的阵列,非常适合逻辑接口电平数字电路(例 如 TTL,CMOS 或PMOS 上/NMOS)和较高的电流/电压,如电灯电磁阀,继电器,打印机或其他类似的负…...

若依springboot接入feign踩坑记录
问题情境: 简单的项目采用了若依的前后端分离版本单体应用,之前采用forest请求调用第三方接口,改为feign接口调用后,引入feign报错 error creating bean with name ‘configurationPropertiesbean’ 解决方案: spri…...

Lumerical Script ------ Error: <文件目录> line x:syntax error
Lumerical Script ------ Error: <文件目录> line x:syntax error 引言正文引言 在 Lumerical Script ------ Error: line 0: syntax error 一文中我们介绍了一种常见的错误提示信息。这里,我们使用类似的代码,介绍另一种提示错误提示信息。 正文 有时候,当我们在…...

Opencv基础与学习路线
Opencv Opencv每一篇目具体: Opencv(1)读取与图像操作 Opencv(2)绘图与图像操作 Opencv(3)详解霍夫变换 Opencv(4)详解轮廓 Opencv(5)平滑处理 具体Opencv相关demo代码欢迎访问我的github仓库(包含python和c代码) demo代码 文章目录 Opencv一…...

Python装饰器的使用详解
目录 1、函数装饰器 1.1、闭包函数 1.2、装饰器语法 1.3、装饰带参数的函数 1.4、被装饰函数的身份问题 1.4.1、解决被装饰函数的身份问题 1.5、装饰器本身携带/传参数 1.6、嵌套多个装饰器 2、类装饰器 装饰器顾名思义作为一个装饰的作用,本身不改变被装…...
基于springboot+vue的党员教育和管理系统
博主主页:猫头鹰源码 博主简介:Java领域优质创作者、CSDN博客专家、阿里云专家博主、公司架构师、全网粉丝5万、专注Java技术领域和毕业设计项目实战,欢迎高校老师\讲师\同行交流合作 主要内容:毕业设计(Javaweb项目|小程序|Pyt…...

三个伪类让你的CSS代码更加优雅
公众号:程序员白特,欢迎一起交流学习~ 原文:CSS整洁之道——:is()、:where()和:has()的用法 - 掘金 (juejin.cn) 让我们写出优雅界面的CSS,它也总是把自己进化得更加优雅。 今天我们花5分钟时间学习三个优雅的CSS伪类:…...
。】2022-5-15)
【根据当天日期输出明天的日期(需对闰年做判定)。】2022-5-15
缘由根据当天日期输出明天的日期(需对闰年做判定)。日期类型结构体如下: struct data{ int year; int month; int day;};-编程语言-CSDN问答 struct mdata{ int year; int month; int day; }mdata; int 天数(int year, int month) {switch (month){case 1: case 3:…...

从WWDC看苹果产品发展的规律
WWDC 是苹果公司一年一度面向全球开发者的盛会,其主题演讲展现了苹果在产品设计、技术路线、用户体验和生态系统构建上的核心理念与演进脉络。我们借助 ChatGPT Deep Research 工具,对过去十年 WWDC 主题演讲内容进行了系统化分析,形成了这份…...

如何在看板中体现优先级变化
在看板中有效体现优先级变化的关键措施包括:采用颜色或标签标识优先级、设置任务排序规则、使用独立的优先级列或泳道、结合自动化规则同步优先级变化、建立定期的优先级审查流程。其中,设置任务排序规则尤其重要,因为它让看板视觉上直观地体…...

Frozen-Flask :将 Flask 应用“冻结”为静态文件
Frozen-Flask 是一个用于将 Flask 应用“冻结”为静态文件的 Python 扩展。它的核心用途是:将一个 Flask Web 应用生成成纯静态 HTML 文件,从而可以部署到静态网站托管服务上,如 GitHub Pages、Netlify 或任何支持静态文件的网站服务器。 &am…...

CRMEB 框架中 PHP 上传扩展开发:涵盖本地上传及阿里云 OSS、腾讯云 COS、七牛云
目前已有本地上传、阿里云OSS上传、腾讯云COS上传、七牛云上传扩展 扩展入口文件 文件目录 crmeb\services\upload\Upload.php namespace crmeb\services\upload;use crmeb\basic\BaseManager; use think\facade\Config;/*** Class Upload* package crmeb\services\upload* …...

使用 SymPy 进行向量和矩阵的高级操作
在科学计算和工程领域,向量和矩阵操作是解决问题的核心技能之一。Python 的 SymPy 库提供了强大的符号计算功能,能够高效地处理向量和矩阵的各种操作。本文将深入探讨如何使用 SymPy 进行向量和矩阵的创建、合并以及维度拓展等操作,并通过具体…...

MySQL账号权限管理指南:安全创建账户与精细授权技巧
在MySQL数据库管理中,合理创建用户账号并分配精确权限是保障数据安全的核心环节。直接使用root账号进行所有操作不仅危险且难以审计操作行为。今天我们来全面解析MySQL账号创建与权限分配的专业方法。 一、为何需要创建独立账号? 最小权限原则…...

无人机侦测与反制技术的进展与应用
国家电网无人机侦测与反制技术的进展与应用 引言 随着无人机(无人驾驶飞行器,UAV)技术的快速发展,其在商业、娱乐和军事领域的广泛应用带来了新的安全挑战。特别是对于关键基础设施如电力系统,无人机的“黑飞”&…...
的使用)
Go 并发编程基础:通道(Channel)的使用
在 Go 中,Channel 是 Goroutine 之间通信的核心机制。它提供了一个线程安全的通信方式,用于在多个 Goroutine 之间传递数据,从而实现高效的并发编程。 本章将介绍 Channel 的基本概念、用法、缓冲、关闭机制以及 select 的使用。 一、Channel…...

uniapp 开发ios, xcode 提交app store connect 和 testflight内测
uniapp 中配置 配置manifest 文档:manifest.json 应用配置 | uni-app官网 hbuilderx中本地打包 下载IOS最新SDK 开发环境 | uni小程序SDK hbulderx 版本号:4.66 对应的sdk版本 4.66 两者必须一致 本地打包的资源导入到SDK 导入资源 | uni小程序SDK …...
