备战蓝桥杯---动态规划的一些思想1
话不多说,直接看题:
目录
1.双线程DP
2.正难则反+多组DP
3.换个方向思考:
1.双线程DP

可能有人会说直接贪心:先选第1条的最优路径,再选第2条最优路径。
其实我们再选第1条时,我们怎么选会对第2条的路径产生影响,不满足无后效性。
我们选另一种思路:我们可以把问题看作A同时向B传2张纸条,我们令f[i][j][m][n]表示一张纸条在(i,j),另一个在(m,n)时的最优值,这样就满足了无后效性。
易得转移方程:
f[i][j][m][n]=a[i][j]+a[m][n]+max(f[i-1][j][m-1][n],f[i-1][j][m][n-1],f[i][j-1][m-1][n],f[i][j-1][m][n-1]).
同时,我们令f[i][j][i][j]为负无穷即可。
下面是AC代码:
#include<bits/stdc++.h>
using namespace std;
int m,n,a[60][60],dp[52][52][52][52];
int f(int i,int j,int x,int y){if(dp[i][j][x][y]!=-1){return dp[i][j][x][y];}if(i==x&&j==y) return dp[i][j][x][y]=-10000000;if(i-1>=1&&x-1>=1) dp[i][j][x][y]=max(dp[i][j][x][y],f(i-1,j,x-1,y));if(i-1>=1&&y-1>=1) dp[i][j][x][y]=max(dp[i][j][x][y],f(i-1,j,x,y-1));if(j-1>=1&&x-1>=1) dp[i][j][x][y]=max(dp[i][j][x][y],f(i,j-1,x-1,y));if(j-1>=1&&y-1>=1) dp[i][j][x][y]=max(dp[i][j][x][y],f(i,j-1,x,y-1));dp[i][j][x][y]+=a[i][j]+a[x][y];return dp[i][j][x][y];
}
int main(){cin>>m>>n;memset(dp,-1,sizeof(dp));dp[1][1][1][1]=0;for(int i=1;i<=m;i++){for(int j=1;j<=n;j++){cin>>a[i][j];}}cout<<f(m-1,n,m,n-1);
}接题:
2.正难则反+多组DP
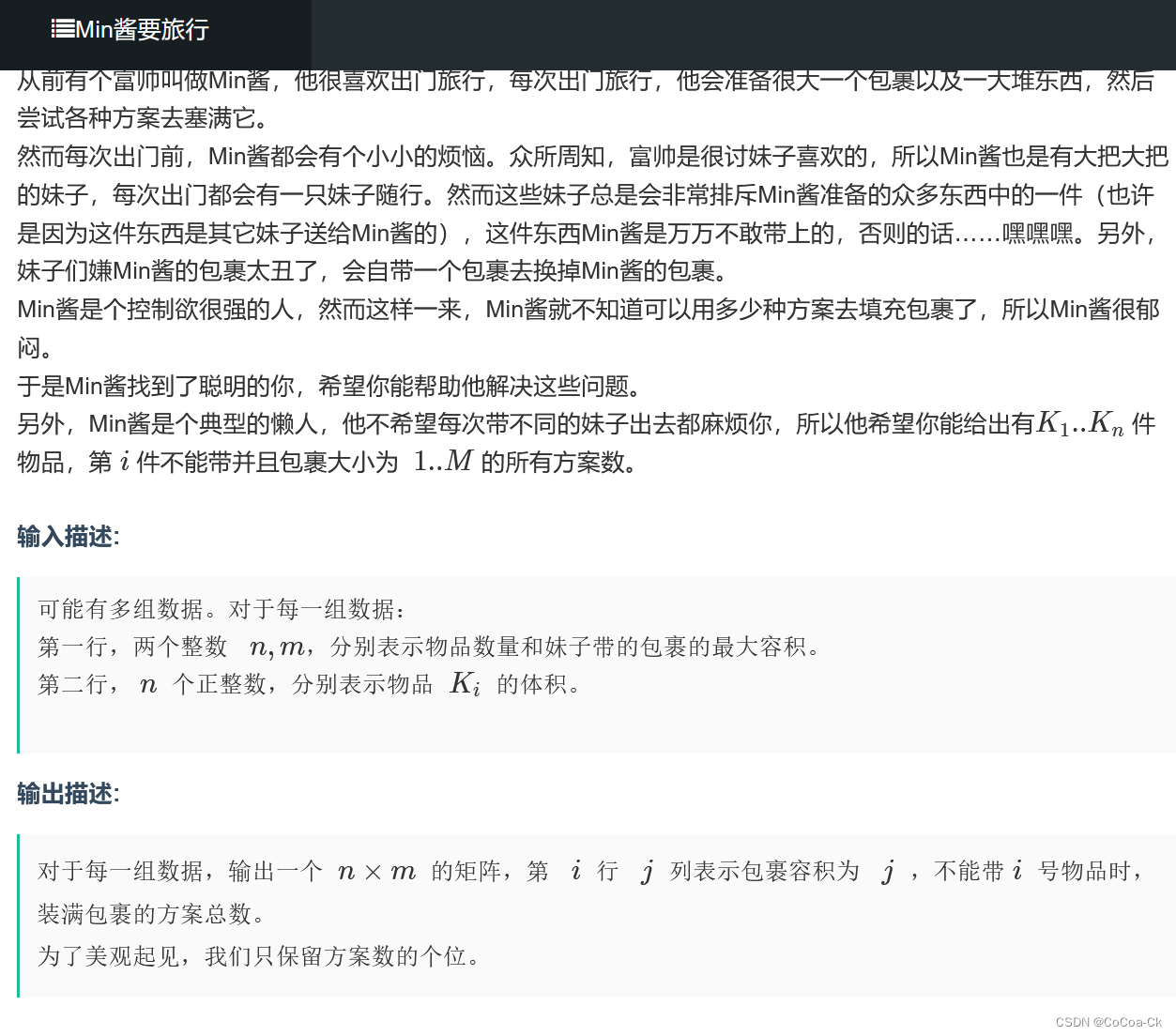
我们自然地想到用g[i][j]表示第i件物品不能带,背包大小为j的方案数。
直接求无从下手,我们考虑他其实就是背包大小为j的方案数-g[i][j-v[i]].
下面是AC代码:
#include<bits/stdc++.h>
using namespace std;
#define mod 10
int n,m,f[2350][2350],g[2350][2350],k[2350];
int main(){cin>>n>>m;for(int i=1;i<=n;i++) cin>>k[i];f[0][0]=1;for(int i=1;i<=n;i++){for(int j=0;j<=m;j++){if(j<k[i]) f[i][j]=f[i-1][j]%mod;else{f[i][j]=(f[i-1][j]%mod+f[i-1][j-k[i]]%mod)%mod;}}}for(int i=1;i<=n;i++){for(int j=1;j<=m;j++){if(j<k[i]) g[i][j]=f[n][j];else if(j==k[i]) g[i][j]=(f[n][j]-1+mod)%mod;else g[i][j]=(f[n][j]%mod-g[i][j-k[i]]%mod+mod)%mod;cout<<g[i][j]%mod;}cout<<endl;}
}接题:
3.换个方向思考:

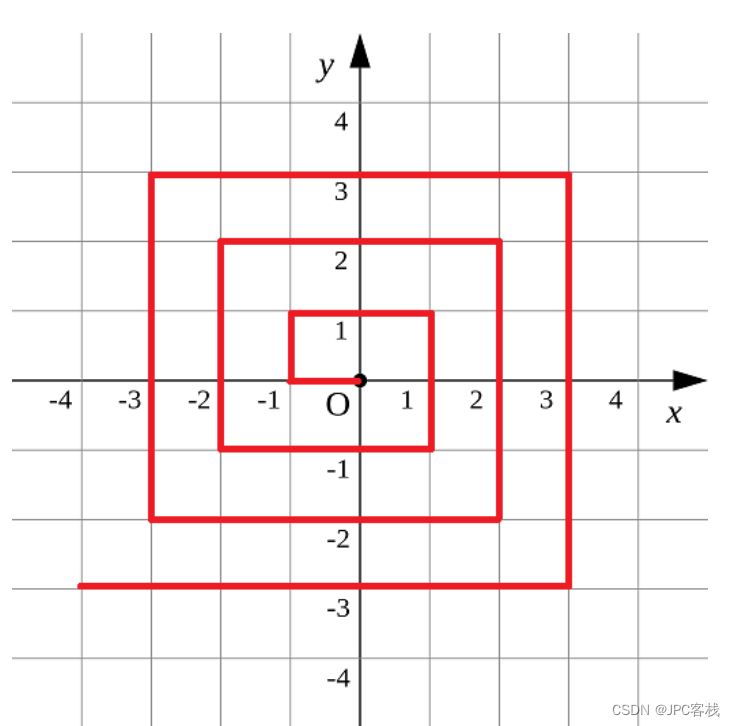
如果我们一行一行看,不像互不侵犯可以枚举,于是我们换个角度,我们斜着看,即:

我们发现,在斜着的一列,要敲某一个则必须把他斜上方的都敲了,因此,我们一定是敲的靠上的斜着的某一段。
同时他靠右的一斜列至少要敲到他的层数-1.这样子就合法了。
我们令f[i][j][k]表示前i列共敲了j块,第i列敲了k块。
易得转移方程:
f[i][j][k]=max(f[i-1][j-k][0--(k+1)]+sum[i][k]]).
下面是AC代码:
#include<bits/stdc++.h>
using namespace std;
int n,m,a[60][60],sum[60][60],dp[55][510][55];
int main(){cin>>n>>m;for(int i=1;i<=n;i++){for(int j=1;j<=n-i+1;j++){cin>>a[i][j];}}for(int i=1;i<=n;i++){for(int j=1;j<=n-i+1;j++){sum[i][j]=sum[i-1][j]+a[i][j];}}int ans=0;memset(dp,-0x3f,sizeof(dp));dp[n][0][0]=0;dp[n][1][1]=a[1][n];for(int i=n-1;i>=1;i--){for(int j=0;j<=m;j++){for(int k=0;k<=min(n-i+1,j);k++){for(int w=max(k-1,0);w<=n-i;w++){dp[i][j][k]=max(sum[k][i]+dp[i+1][j-k][w],dp[i][j][k]);ans=max(ans,dp[i][j][k]);}}}}cout<<ans;
}相关文章:

备战蓝桥杯---动态规划的一些思想1
话不多说,直接看题: 目录 1.双线程DP 2.正难则反多组DP 3.换个方向思考: 1.双线程DP 可能有人会说直接贪心:先选第1条的最优路径,再选第2条最优路径。 其实我们再选第1条时,我们怎么选会对第2条的路径…...

基于BERTopic模型的中文文本主题聚类及可视化
文章目录 BERTopic简介模型加载地址文本加载数据处理BERTopic模型构建模型结果展示主题可视化总结BERTopic简介 BERTopic论文地址:BERTopic: Neural topic modeling with a class-based TF-IDF procedure BERTopic是一种结合了预训练模型BERT和主题建模的强大工具。它允许我…...
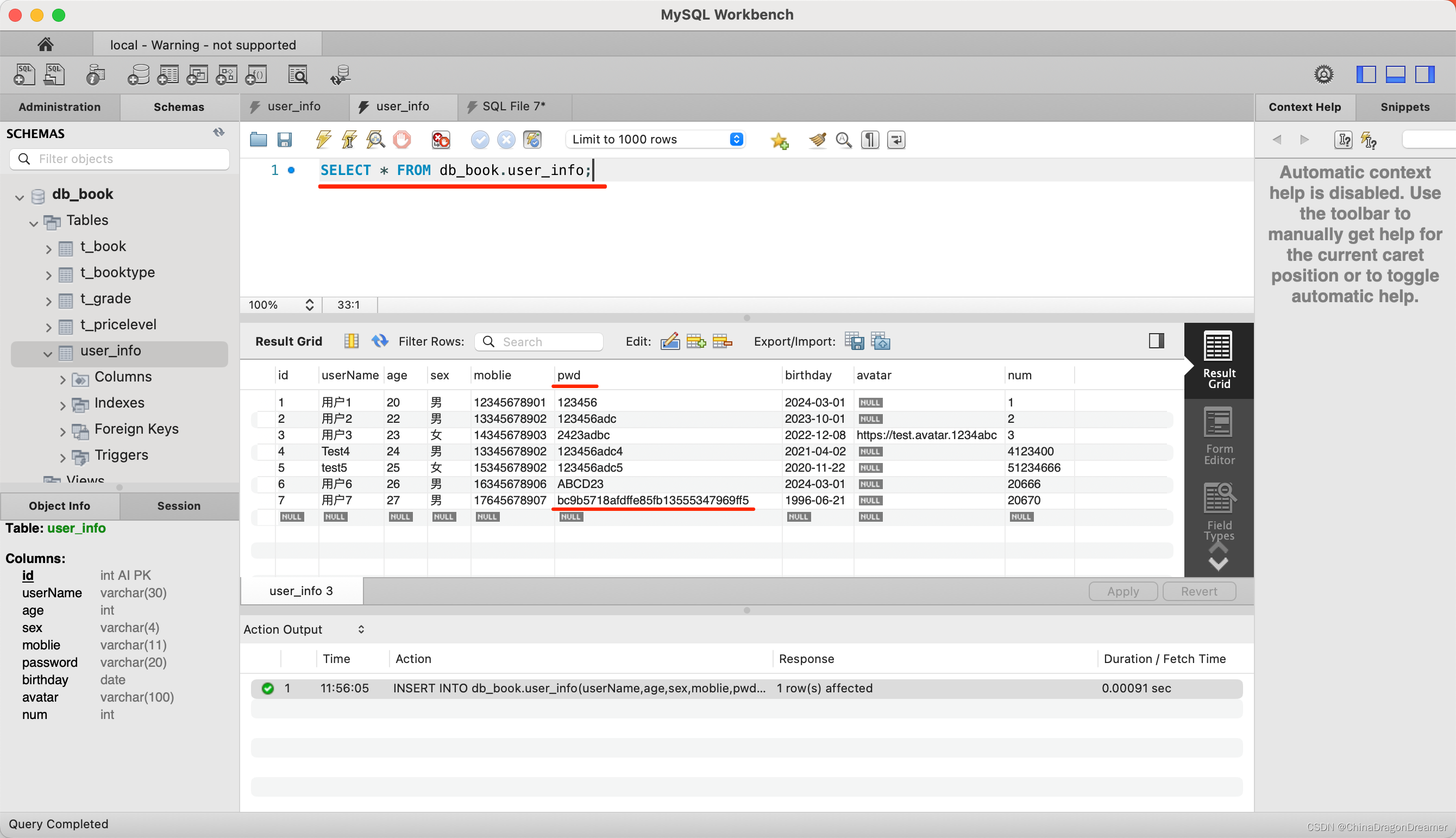
MySQL:函数
提醒: 设定下面的语句是在数据库名为 db_book里执行的。 创建user_info表 注意:pwd为密码字段,这里使用了VARCHAR(128)类型,为了后面方便对比,开发项目里一般使用char(32),SQL语句里使用MD5加密函数 USE db…...
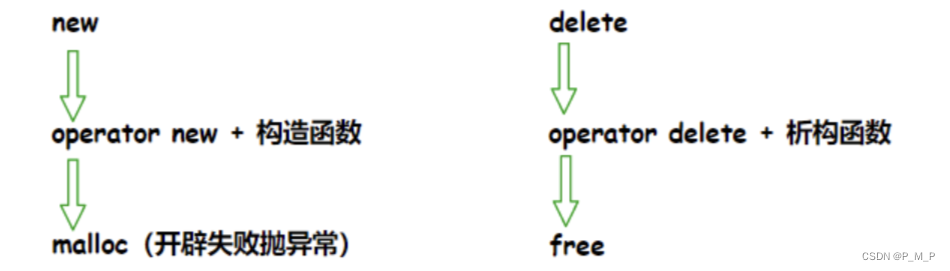
C/C++内存管理及内存泄漏详解
目录 C/C内存分布 C语言中动态内存管理方式:malloc/calloc/realloc/free C内存管理方式 new/delete操作内置类型 new和delete操作自定义类型 operator new与operator delete函数 new和delete的实现原理 内置类型 自定义类型 内存泄漏 概念 内存泄漏分类 ⭐…...
41)
什么是系统工程(字幕)41
0 00:00:01,650 --> 00:00:01,884 好 1 00:00:01,884 --> 00:00:06,330 那这个时候我们就可以把它绑定到上面了 2 00:00:06,610 --> 00:00:07,940 那我们来看 3 00:00:11,710 --> 00:00:12,930 幻灯片上 4 00:00:15,530 --> 00:00:15,885 5 00:00:15,885 --…...

测开新手:pytest+requests+allure自动化测试接入Jenkins学习
最近在这整理知识,发现在pytest的知识文档缺少系统性,这里整理一下,方便后续回忆。 在python中,大家比较熟悉的两个框架是unittest和pytest: Unittest是Python标准库中自带的单元测试框架,Unittest有时候…...
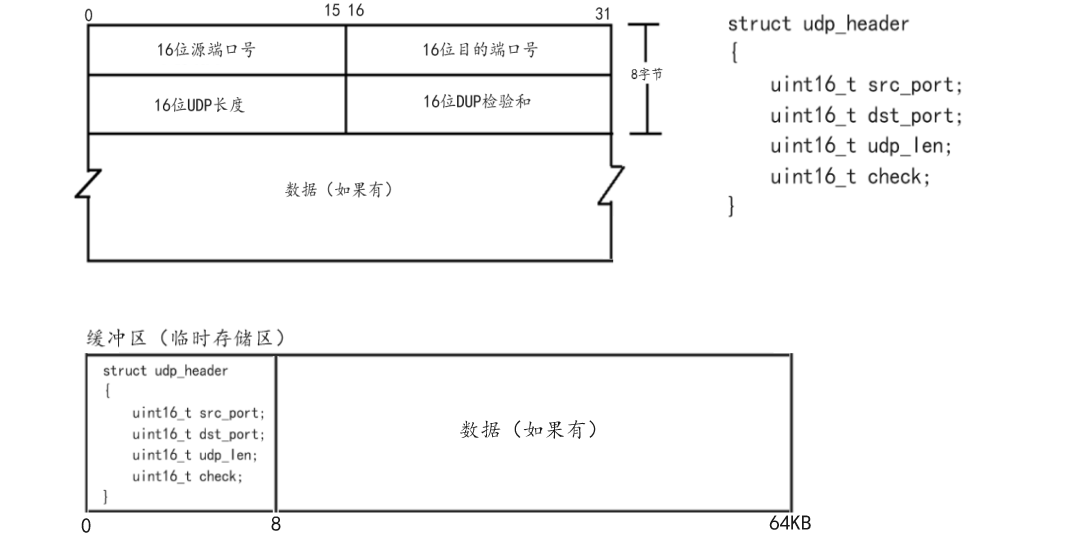
学习网络编程No.11【传输层协议之UDP】
引言: 北京时间:2023/11/20/9:17,昨天成功更文,上周实现了更文两篇,所以这周再接再厉。当然做题任在继续,而目前做题给我的感觉以套路和技巧偏多,还是那句话很多东西不经历你就是不懂ÿ…...

向爬虫而生---Redis 基石篇6 <拓展HyperLogLog>
前言: 继续之前的 向爬虫而生---Redis 基石篇5 <拓展Zset>-CSDN博客 一些比较基础的redis类型在初中级阶段用着没有毛病,但是到了大数据时代,慢慢一些更高级的场景,就需要把这几个类型搬出来了! 正文: 概念: 当我们需要对一个大型数据集进行去重计…...

JavaScript中的this
在实际应用中,了解 this 的行为是非常重要的,特别是在编写库或框架时,或者当你需要在回调函数中访问特定的上下文时,通常推荐使用箭头函数或者其他方法来确保 this 的正确指向。 在ES6中,this 的值取决于它是如何被调用…...

宝塔php站点设置伪静态规则 访问 a.com 时候跳转到 a.com/b.html
要在宝塔 PHP 站点中设置伪静态规则,实现访问a.com时跳转到a.com/b.html,可以按照以下步骤进行操作: 打开宝塔面板并登录到你的服务器管理界面。进入网站设置页面,找到你要设置伪静态规则的 PHP 站点。在站点设置中,找…...
git介绍4.2
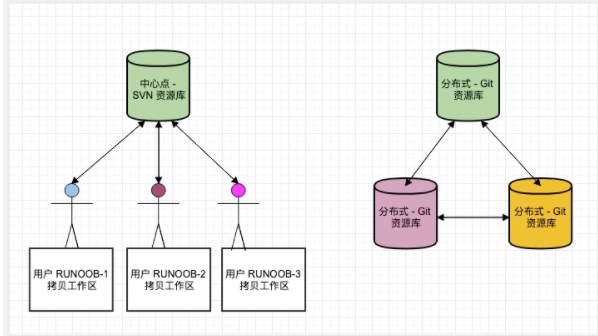
git(版本控制工具) 一、git 介绍 1、git是目前世界上最先进的分布式版本控制系统,可以有效,高速的处理从小到大的项目版本管理。 2、git是linux torvalds 为了帮助管理linux内核开发二开发的一个开放源码的版本控制软件。 3、git作用:更好…...

【深入了解设计模式】组合设计模式
组合设计模式 组合模式是一种结构型设计模式,它允许你将对象组合成树状结构来表现“整体-部分”关系。组合模式使得客户端可以统一对待单个对象和组合对象,从而使得代码更加灵活和易于扩展。 概述 对于这个图片肯定会非常熟悉,上图我们可…...

4.Java---方法+重载
方法 方法的调用是需要开辟内存的,方法调用结束内存就被销毁了. 下面将介绍一个经典的错误标准的0分的示意! 我们日常中写交换两个数字的代码的时候都会用如下的方法进行描述: 你是不是觉得自己写的特别对!终于可以独立写一个小小的函数了? 下面运行一下看看结果 哦莫!怎么…...
蓝桥杯Java B组历年真题(2013年-2021年)
一、2013年真题 1、世纪末的星期 使用日期类判断就行,这里使用LocalDate,也可以使用Calendar类 答案 2099 使用LocalDate import java.time.LocalDate; import java.time.format.DateTimeFormatter; // 1:无需package // 2: 类名必须Main, 不可修改p…...
C++笔记(五)--- 虚函数(virtual)
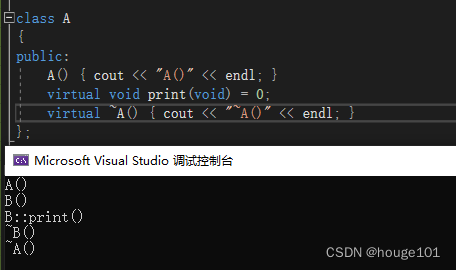
目录 虚函数介绍 虚函数、覆盖和重载区别 虚函数介绍 C的虚函数是多态性的表现 1.构造函数不能为虚函数2.子类继承时虚函数仍为虚函数3.虚函数类外实现时,不需要加virtual4.有虚函数的类,析构函数一定要写成虚函数(否则可能会造成内存泄漏&…...

编写加密程序,加密规则为:将所有字母转化为该字母后的第三个字母,即A->D、B->E
编写加密程序,加密规则为:将所有字母转化为该字母后的第三个字母,即A->D、B->E、C->F、…、Y->B、Z->C。小写字母同上,其他字符不做转化。输入任意字符串,输出加密后的结果。 例如:输入&qu…...

【笔记】:更方便的将一个List中的数据传入另一个List中,避免多重循环
这里是 simpleInfoList 集合,记为集合A(传值对象) List<CourseSimpleInfoDTO> simpleInfoList courseClient.getSimpleInfoList(courseIds);if(simpleInfoListnull){throw new BizIllegalException("当前课程不存在!");}这…...
Cisco Secure ACS 5.8.0.32 安装 + Crack 教程
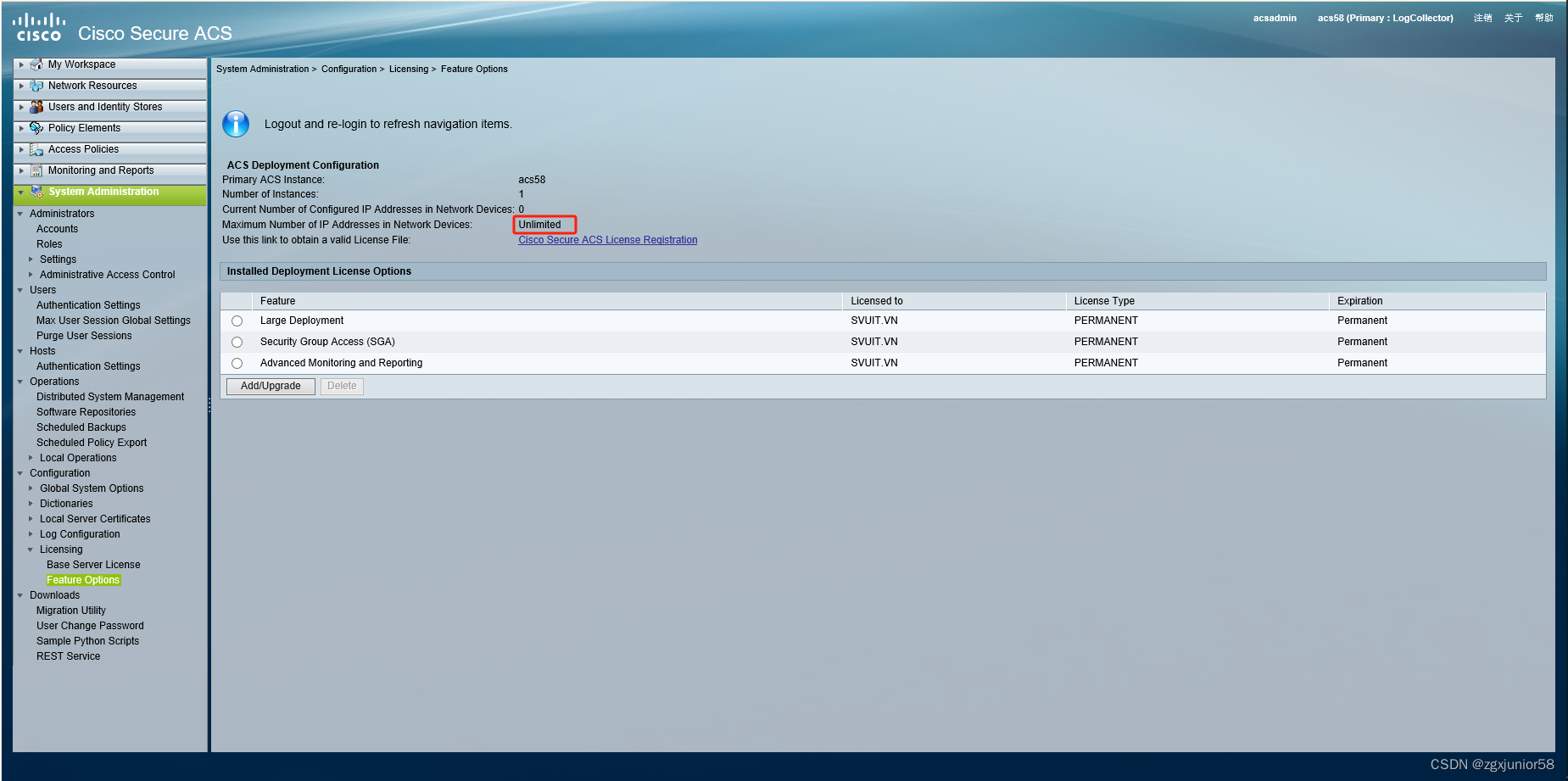
Cisco Secure ACS 5.8.0.32 安装 Crack 教程 前言系统环境开始安装 开始破解导入授权文件 前言 在ESXi 6.7 上经历过无数次的安装尝试 测试了各种兼容版本都没有安装成功,记最后一次安装成功的过程. 系统环境 服务器 : Dell R720xd CPU : E5-2620 v2 系统 : ESXi 6.7…...

项目准备March
Nginx主要用来作为Http服务器,要实现Tomcat的负载均衡,就可以通过Nginx来实现。 正向代理代理的是客户端,反向代理代理的是服务端。SpringBoot采用约定优于配置的思想,简化Spring项目的配置开发。 前端请求其实并未直接发送到后…...
集智书童 | YOLO+混合注意力机制 | YOLOv5再加4.3%才可以做对手,Transformer混合设计依旧可以卷
本文来源公众号“集智书童”,侵权删,干货满满。YOLOv5重出江湖! 原文链接:https://mp.weixin.qq.com/s/vb7HsA0fKDgRc3uC8Z-2yw 在工业生产过程中,由于低效率、不统一的评估、高成本以及缺乏实时数据,传统…...

OpenLayers 可视化之热力图
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 热力图(Heatmap)又叫热点图,是一种通过特殊高亮显示事物密度分布、变化趋势的数据可视化技术。采用颜色的深浅来显示…...

Unity3D中Gfx.WaitForPresent优化方案
前言 在Unity中,Gfx.WaitForPresent占用CPU过高通常表示主线程在等待GPU完成渲染(即CPU被阻塞),这表明存在GPU瓶颈或垂直同步/帧率设置问题。以下是系统的优化方案: 对惹,这里有一个游戏开发交流小组&…...

.Net框架,除了EF还有很多很多......
文章目录 1. 引言2. Dapper2.1 概述与设计原理2.2 核心功能与代码示例基本查询多映射查询存储过程调用 2.3 性能优化原理2.4 适用场景 3. NHibernate3.1 概述与架构设计3.2 映射配置示例Fluent映射XML映射 3.3 查询示例HQL查询Criteria APILINQ提供程序 3.4 高级特性3.5 适用场…...

PPT|230页| 制造集团企业供应链端到端的数字化解决方案:从需求到结算的全链路业务闭环构建
制造业采购供应链管理是企业运营的核心环节,供应链协同管理在供应链上下游企业之间建立紧密的合作关系,通过信息共享、资源整合、业务协同等方式,实现供应链的全面管理和优化,提高供应链的效率和透明度,降低供应链的成…...

为什么需要建设工程项目管理?工程项目管理有哪些亮点功能?
在建筑行业,项目管理的重要性不言而喻。随着工程规模的扩大、技术复杂度的提升,传统的管理模式已经难以满足现代工程的需求。过去,许多企业依赖手工记录、口头沟通和分散的信息管理,导致效率低下、成本失控、风险频发。例如&#…...

2025盘古石杯决赛【手机取证】
前言 第三届盘古石杯国际电子数据取证大赛决赛 最后一题没有解出来,实在找不到,希望有大佬教一下我。 还有就会议时间,我感觉不是图片时间,因为在电脑看到是其他时间用老会议系统开的会。 手机取证 1、分析鸿蒙手机检材&#x…...

EtherNet/IP转DeviceNet协议网关详解
一,设备主要功能 疆鸿智能JH-DVN-EIP本产品是自主研发的一款EtherNet/IP从站功能的通讯网关。该产品主要功能是连接DeviceNet总线和EtherNet/IP网络,本网关连接到EtherNet/IP总线中做为从站使用,连接到DeviceNet总线中做为从站使用。 在自动…...

OPenCV CUDA模块图像处理-----对图像执行 均值漂移滤波(Mean Shift Filtering)函数meanShiftFiltering()
操作系统:ubuntu22.04 OpenCV版本:OpenCV4.9 IDE:Visual Studio Code 编程语言:C11 算法描述 在 GPU 上对图像执行 均值漂移滤波(Mean Shift Filtering),用于图像分割或平滑处理。 该函数将输入图像中的…...

elementUI点击浏览table所选行数据查看文档
项目场景: table按照要求特定的数据变成按钮可以点击 解决方案: <el-table-columnprop"mlname"label"名称"align"center"width"180"><template slot-scope"scope"><el-buttonv-if&qu…...

深度学习之模型压缩三驾马车:模型剪枝、模型量化、知识蒸馏
一、引言 在深度学习中,我们训练出的神经网络往往非常庞大(比如像 ResNet、YOLOv8、Vision Transformer),虽然精度很高,但“太重”了,运行起来很慢,占用内存大,不适合部署到手机、摄…...
