代码随想录算法训练营第四十四天 完全背包 、零钱兑换 II 、组合总和 Ⅳ
代码随想录算法训练营第四十四天 | 完全背包 、零钱兑换 II 、组合总和 Ⅳ
完全背包
题目链接:题目页面 (kamacoder.com)
解释一、01背包 一维 :为什么要倒序遍历背包?
首先要明白二维数组的递推过程,然后才能看懂二维变一维的过程。
假设目前有背包容量为10,可以装的最大价值, 记为g(10)。
即将进来的物品重量为6。价值为9。
那么此时可以选择装该物品或者不装该物品。
如果不装该物品,显然背包容量无变化,这里对应二维数组,其实就是取该格子上方的格子复制下来,就是所说的滚动下来,直接g【10】 = g【10】,这两个g【10】要搞清楚,右边的g【10】是上一轮记录的,也就是对应二维数组里上一层的值,而左边是新的g【10】,也就是对应二维数组里下一层的值。
如果装该物品,则背包容量= g(10-6) = g(4) + 9 ,也就是 g(10) = g(4) + 6 ,这里的6显然就是新进来的物品的价值,g(10)就是新记录的,对应二维数组里下一层的值,而这里的g(4)是对应二维数组里上一层的值,通俗的来讲:你要找到上一层也就是上一状态下 背包容量为4时的能装的最大价值,用它来更新下一层的这一状态,也就是加入了价值为9的物品的新状态。
这时候如果是正序遍历会怎么样? g(10) = g(4) + 6 ,这个式子里的g(4)就不再是上一层的了,因为你是正序啊,g(4) 比g(10)提前更新,那么此时程序已经没法读取到上一层的g(4)了,新更新的下一层的g(4)覆盖掉了,这里也就是为啥有题解说一件物品被拿了两次的原因。
解释二、01背包到底先遍历物品还是先遍历背包呢?
其实在二维的时候,即使是先遍历背包重量,再遍历物品重量,你真的画图的时候会发现,永远的数据来源,依旧还是max(不放,放)= max(正上方的值,左上角的值)。
那你在一维的时候,如果先遍历背包容量的话:
如果你还是从左到右地遍历背包容量:一样会造成重复添加;
如果你从右到左地遍历背包容量:相当于你的计算顺序是先竖着写完第四列,再竖着写完第三列,再竖着写完第二列。。。但你写第四列的时候,第三列全部都是空的,左边是没有数据的,你永远只在累加正上方的数。而如果你是先遍历物品再遍历背包,你的填空顺序是,先写第一行(从右往左写),再写第二行的时候,你的左边是有数字的。。。
那你可能想问,我能不能做一个竖着的表格更新呢?其实没有帮助的,你只要先一股脑地竖着算,你永远没法利用起左边格子的数字——无法利用之前格子的数,那就不是动态规划了
解释三、为什么完全背包可以颠倒物品和背包的遍历顺序?
请想像一下 01背包的二维dp数组图像 和 完全背包的二维dp数组图像
01背包 的二维数组dp[i] [j]只取决于其左上角的值,所以 使用二维数组时可以从对物品和背包数组进行正序遍历,且先物品还是先背包可以颠倒
01背包的一维数组dp[j] 因为
背包必须要倒序遍历(参考上面解释一、01背包 一维 :为什么要倒序遍历背包)
↓
如果遍历背包容量放在上一层,那么每个dp[j]就只会放入一个物品,即:背包里只放入了一个物品(解释二)
↓
所以要先物品后背包
完全背包其dp[j]完全取决于
// 先遍历物品再遍历背包
import java.util.*;public class Main {public static void main (String[] args) {Scanner sc = new Scanner(System.in);int N = sc.nextInt();int V = sc.nextInt();int[] weights = new int[N];int[] values = new int[N];for(int i = 0; i < N; ++i) {weights[i] = sc.nextInt();values[i] = sc.nextInt();}int[] dp = new int[V + 1];for(int i = 0; i < N; ++i) {for(int j = weights[i]; j <= V; ++j) {dp[j] = Math.max(dp[j], dp[j - weights[i]] + values[i]);}}System.out.println(dp[V]);}
}
// 先遍历背包再遍历物品
import java.util.*;public class Main {public static void main (String[] args) {Scanner sc = new Scanner(System.in);int N = sc.nextInt();int V = sc.nextInt();int[] weights = new int[N];int[] values = new int[N];for(int i = 0; i < N; ++i) {weights[i] = sc.nextInt();values[i] = sc.nextInt();}int[] dp = new int[V + 1];for(int j = 1; j <= V; ++j) {for(int i = 0; i < N; ++i) {if(j >= weights[i]) {dp[j] = Math.max(dp[j], dp[j - weights[i]] + values[i]);} }}System.out.println(dp[V]);}
}
零钱兑换 II
题目链接:518. 零钱兑换 II - 力扣(LeetCode)
这道题就是 494. 目标和 - 力扣(LeetCode)的完全背包版本
如果求组合数就是外层for循环遍历物品,内层for遍历背包。
如果求排列数就是外层for遍历背包,内层for循环遍历物品。
class Solution {public int change(int amount, int[] coins) {// 硬币数量不限 -> 完全背包// dp[j] 表示:填满j(包括j)这么大容积的包,有dp[j]种方法int[] dp = new int[amount + 1];// dp[0] = 1是 递归公式的基础。如果dp[0] = 0 的话,后面所有推导出来的值都是0了。dp[0] = 1;// 因为纯完全背包求得装满背包的最大价值是多少,和凑成总和的元素有没有顺序没关系,即:有顺序也行,没有顺序也行!// 而本题要求凑成总和的组合数,元素之间明确要求没有顺序/**以coins[0] = 1, coins[1] = 5, amount = 6为例先遍历物品,就是先把1加入计算,然后再把5加入计算 -> 这样得到的是 组合先遍历背包,背包容量的每一个值,都是经过 1 和 5 的计算,包含了{1, 5} 和 {5, 1}两种情况-> 这样得到的是 排列 不理解的话可以打印dp数组来看看*/for(int i = 0; i < coins.length; ++i) {for(int j = coins[i]; j <= amount; ++j) {dp[j] += dp[j - coins[i]];}for(int ele : dp) {System.out.print(ele + ",");}System.out.println(" ");}return dp[amount];}
}
组合总和 Ⅳ
题目链接:377. 组合总和 Ⅳ - 力扣(LeetCode)
本题与动态规划:518.零钱兑换II (opens new window)就是一个鲜明的对比,一个是求排列,一个是求组合,遍历顺序完全不同
class Solution {public int combinationSum4(int[] nums, int target) {int[] dp = new int[target + 1];dp[0] = 1;for (int i = 0; i <= target; i++) {for (int j = 0; j < nums.length; j++) {if (i >= nums[j]) {dp[i] += dp[i - nums[j]];}}}return dp[target];}
}
相关文章:

代码随想录算法训练营第四十四天 完全背包 、零钱兑换 II 、组合总和 Ⅳ
代码随想录算法训练营第四十四天 | 完全背包 、零钱兑换 II 、组合总和 Ⅳ 完全背包 题目链接:题目页面 (kamacoder.com) 解释一、01背包 一维 :为什么要倒序遍历背包? 首先要明白二维数组的递推过程,然后才能看懂二维变一维的…...
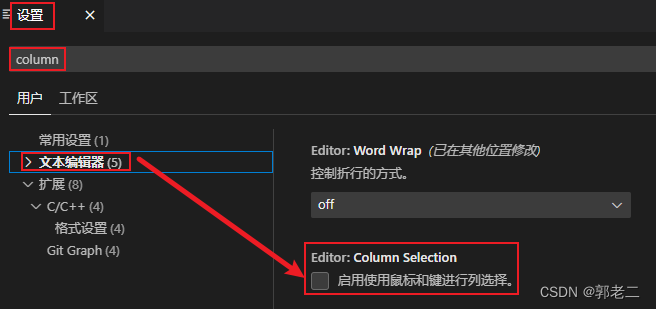
【经验】vscode 鼠标拖曳不能选中整行文字,只能选中纵向矩形范围
1、问题描述 不知道昨天操作vscode设置界面时,误选择了啥,导致鼠标拖曳不能选中整行文字,只能选中纵向矩形范围,现象如下: 2、解决方法 1)打开设置界面 点击左下角按键,选择“设置” 2&…...

Redis--事务机制的详解及应用
Redis事务的概念: Redis事务就是将一系列命令包装成一个队列,在执行时候按照添加的顺序依次执行,中间不会被打断或者干扰,在执行事务中,其他客户端提交的命令不可以插入到执行事务的队列中,简单来说Redis事…...

路由器端口映射如何配置?
在网络通信中,路由器是一个重要的设备,它负责将数据包从一个网络传输到另一个网络。路由器的端口映射配置是一种重要的设置,可以使外部网络中的计算机通过访问路由器上的特定端口与内部网络中的计算机进行通信。本文将介绍什么是路由器端口映…...
力扣34. 在排序数组中查找元素的第一个和最后一个位置(二分查找)
Problem: 34. 在排序数组中查找元素的第一个和最后一个位置 文章目录 题目描述思路复杂度Code 题目描述 思路 Problem: 二分查找常用解题模板(带一道leetcode题目) 直接套用上述中的寻找左、右边界的二分查找模板即可 复杂度 时间复杂度: O ( l o g n )…...

【每日一题】3.2 求逆序对
题目描述 给定一个长度为 n的整数数列,请你计算数列中的逆序对的数量。 逆序对的定义如下:对于数列的第 i个和第 j个元素,如果满足 i<j 且 a[i]>a[j],则其为一个逆序对;否则不是。 输入格式 第一行包含整数 n…...
助力智慧医院数字化)
NTP时间源服务器(NTP网络时钟)助力智慧医院数字化
NTP时间源服务器(NTP网络时钟)助力智慧医院数字化 NTP时间源服务器(NTP网络时钟)助力智慧医院数字化 目前计算机网络中各主机和服务器等网络设备的时间基本处于无序的状态。 随着计算机网络应用的不断涌现,计算机的时…...

Benchmark学习笔记
小记一篇Benchmark的学习笔记 1.什么是benchmark 在维基百科中,是这样子讲的 “As computer architecture advanced, it became more difficult to compare the performance of various computer systems simply by looking at their specifications.Therefore, te…...

Linux中的动静态库
目录 一、静态库 (1)静态库的优缺点: (2)Linux下静态库的创建和执行 1.直接编译编辑 2.指定路径和库名 3.用LIBRARY_PATH环境变量来配置路径 二、动态库 (1)动态库的优缺点 ÿ…...
C/C++基础语法
C/C基础语法 文章目录 C/C基础语法头文件经典问题链表链表基础操作 秒数转换闰年斐波那契数列打印n阶菱形曼哈顿距离菱形图案的定义大数计算 输入输出格式化输入输出getline()函数解决cin只读入一个单词的问题fgets读入整行输出字符数组(两种方式puts和printf&#…...
Home Assistant:基于Python的智能家居开源系统详解
Home Assistant:基于Python的智能家居开源系统详解 在数字化和智能化的时代,智能家居系统成为了现代家庭的新宠。它们能够让我们更加方便地控制家中的各种设备,实现自动化和个性化的居住体验。其中,Home Assistant作为一款基于Pyt…...

使用vscode进行简单的多文件编译
安装好必要的插件后(如C/C,code runner等)默认生成task.json即可进行单文件运行 涉及到多文件情况可以修改task.json如下: {"version": "2.0.0","tasks": [{"type": "cppbuild&quo…...

Python实现PPT演示文稿中视频的添加、替换及提取
无论是在教室、会议室还是虚拟会议中,PowerPoint 演示文稿都已成为一种无处不在的工具,用于提供具有影响力的可视化内容。PowerPoint 提供了一系列增强演示的功能,在其中加入视频的功能可以大大提升整体体验。视频可以传达复杂的概念、演示产…...

Mysql学习之MVCC解决读写问题
多版本并发控制 什么是MVCC MVCC (Multiversion Concurrency Control)多版本并发控制。顾名思义,MVCC是通过数据行的多个版本管理来实现数据库的并发控制。这项技术使得在InnoDB的事务隔离级别下执行一致性读操作有了保证。换言之࿰…...

Linux下如何生成coredump文件
引言 在linux下执行程序,当出现coredump时,却发现没有生成core文件,或者生成了core文件却不知道在哪里,下面就讲述如何产出core文件,以及指定core文件的产出格式与路径。 打开core文件的大小限制 ulimit -c unlimit…...
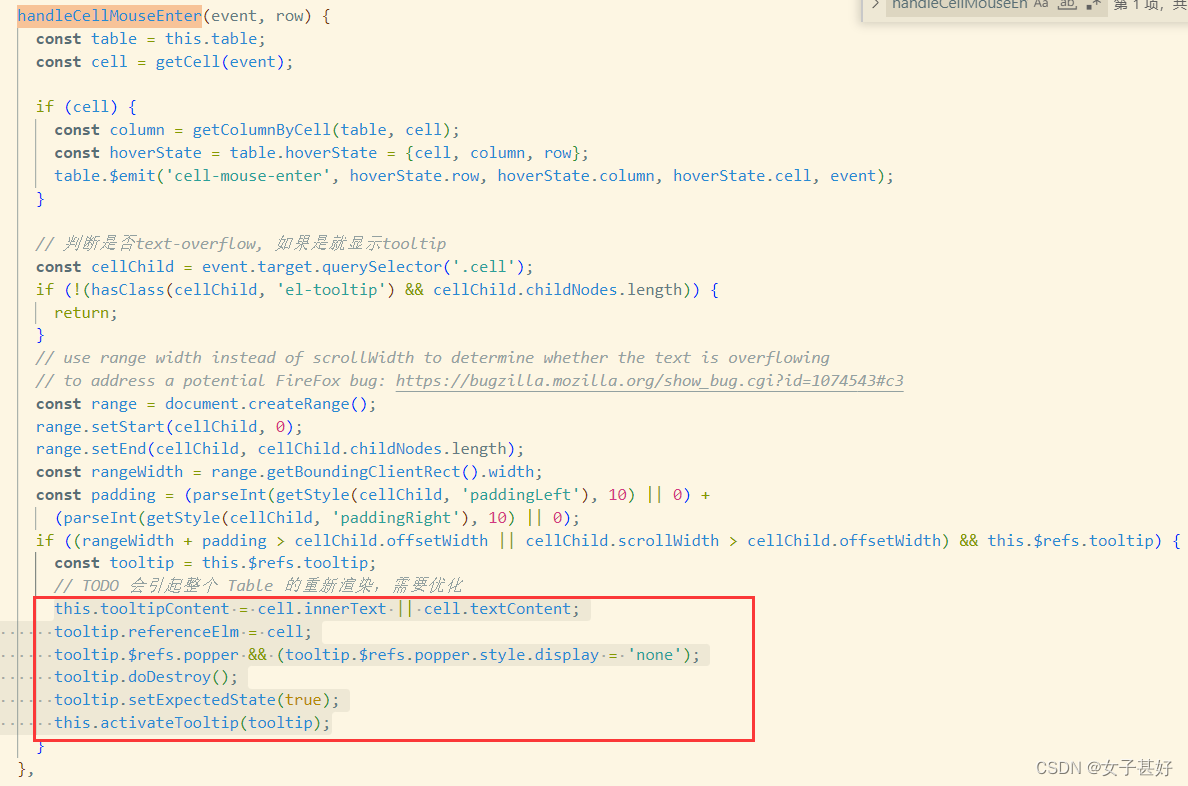
eltable 合计行添加tooltip
eltable 合计行添加tooltip 问题描述: eltable 合计行单元格内容过长会换行,需求要求合计行数据超长显示 … ,鼠标 hover 时显示提示信息。 解决方案:eltable合计行没有对外的修改接口,想法是 自己实现一个tooltip&a…...
)
Secure Boot(安全启动)
Secure Boot(安全启动)的原理基于链式验证,这是一种确保计算机在启动过程中只加载和执行经过认证的软件的机制。这个过程涉及到硬件、固件和操作系统的多个层面。以下是Secure Boot的基本原理: 密钥和证书:Secure Boot…...

大厂面试经验:如何对加密后的数据进行模糊查询操作
加密后的数据对模糊查询不是很友好,本篇就针对加密数据模糊查询这个问题来展开讲一讲实现的思路。 为了数据安全我们在开发过程中经常会对重要的数据进行加密存储,常见的有:密码、手机号、电话号码、详细地址、银行卡号、信用卡验证码等信息…...
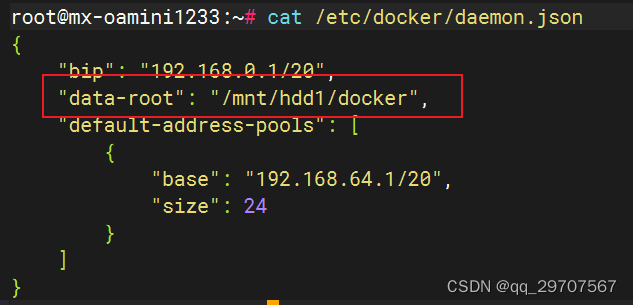
修改docker默认存储位置【高版本的docker】
一、修改docker默认存储位置 1、停服务 systemctl stop docker 2、修改/etc/docker/daemon.json添加新的dcoker路径 如"data-root": "/mnt/hdd1/docker" 3、保存后重启服务:systemctl restart docker 二、其他服务的命令 systemctl disab…...

CleanMyMac X2024免费Mac电脑清理和优化工具
CleanMyMac X是一款专业的 Mac 清理和优化工具,它具备一系列强大的功能,可以帮助用户轻松管理和维护他们的 Mac 电脑。以下是一些关于 CleanMyMac X 的主要功能和特点: 智能清理:CleanMyMac X 能够智能识别并清理 Mac 上的无用文件…...

【Axure高保真原型】引导弹窗
今天和大家中分享引导弹窗的原型模板,载入页面后,会显示引导弹窗,适用于引导用户使用页面,点击完成后,会显示下一个引导弹窗,直至最后一个引导弹窗完成后进入首页。具体效果可以点击下方视频观看或打开下方…...

地震勘探——干扰波识别、井中地震时距曲线特点
目录 干扰波识别反射波地震勘探的干扰波 井中地震时距曲线特点 干扰波识别 有效波:可以用来解决所提出的地质任务的波;干扰波:所有妨碍辨认、追踪有效波的其他波。 地震勘探中,有效波和干扰波是相对的。例如,在反射波…...

智慧医疗能源事业线深度画像分析(上)
引言 医疗行业作为现代社会的关键基础设施,其能源消耗与环境影响正日益受到关注。随着全球"双碳"目标的推进和可持续发展理念的深入,智慧医疗能源事业线应运而生,致力于通过创新技术与管理方案,重构医疗领域的能源使用模式。这一事业线融合了能源管理、可持续发…...

【Go】3、Go语言进阶与依赖管理
前言 本系列文章参考自稀土掘金上的 【字节内部课】公开课,做自我学习总结整理。 Go语言并发编程 Go语言原生支持并发编程,它的核心机制是 Goroutine 协程、Channel 通道,并基于CSP(Communicating Sequential Processes࿰…...

TRS收益互换:跨境资本流动的金融创新工具与系统化解决方案
一、TRS收益互换的本质与业务逻辑 (一)概念解析 TRS(Total Return Swap)收益互换是一种金融衍生工具,指交易双方约定在未来一定期限内,基于特定资产或指数的表现进行现金流交换的协议。其核心特征包括&am…...

IoT/HCIP实验-3/LiteOS操作系统内核实验(任务、内存、信号量、CMSIS..)
文章目录 概述HelloWorld 工程C/C配置编译器主配置Makefile脚本烧录器主配置运行结果程序调用栈 任务管理实验实验结果osal 系统适配层osal_task_create 其他实验实验源码内存管理实验互斥锁实验信号量实验 CMISIS接口实验还是得JlINKCMSIS 简介LiteOS->CMSIS任务间消息交互…...

CMake控制VS2022项目文件分组
我们可以通过 CMake 控制源文件的组织结构,使它们在 VS 解决方案资源管理器中以“组”(Filter)的形式进行分类展示。 🎯 目标 通过 CMake 脚本将 .cpp、.h 等源文件分组显示在 Visual Studio 2022 的解决方案资源管理器中。 ✅ 支持的方法汇总(共4种) 方法描述是否推荐…...

Java线上CPU飙高问题排查全指南
一、引言 在Java应用的线上运行环境中,CPU飙高是一个常见且棘手的性能问题。当系统出现CPU飙高时,通常会导致应用响应缓慢,甚至服务不可用,严重影响用户体验和业务运行。因此,掌握一套科学有效的CPU飙高问题排查方法&…...

JAVA后端开发——多租户
数据隔离是多租户系统中的核心概念,确保一个租户(在这个系统中可能是一个公司或一个独立的客户)的数据对其他租户是不可见的。在 RuoYi 框架(您当前项目所使用的基础框架)中,这通常是通过在数据表中增加一个…...

管理学院权限管理系统开发总结
文章目录 🎓 管理学院权限管理系统开发总结 - 现代化Web应用实践之路📝 项目概述🏗️ 技术架构设计后端技术栈前端技术栈 💡 核心功能特性1. 用户管理模块2. 权限管理系统3. 统计报表功能4. 用户体验优化 🗄️ 数据库设…...
