c++二叉树
二叉树进阶
1.二叉搜索树(binary search tree)
二叉搜索树天然就适合查找,对于满二叉树或者完全二叉树,最多搜索lgn次(就像是有序数组二分查找,每次搜索都会减少范围),极端情况简化成单链表就要走n次,即要走高度次,时间复杂度是O(N)。所以需要用时间复杂度为O(lgn)的AVL树(平衡二叉树)或者RB树(红黑树)解决。
按中序遍历,得到的结果就是有序的,升序;后序删除方便很多,不用保留前面的值;拷贝不可以调用插入,否则结构会发生巨大的变化,而是使用前序来赋值 。
相较于普通的二叉树,增删查改就有了意义,而有序数组二分查找是不可以的,挪动数据效率很低。
二叉搜索树不允许有重复,key一般要唯一。
1.1概念
二叉搜索树又称二叉排序树它或者是一棵空树,或者是具有以下性质的二叉树:
1.若它的左子树不为空,则左子树上所有节点的值都小于根节点的值 ;
2.若它的右子树不为空,则右子树上所有节点的值都大于根节点的值 ;
3.它的左右子树也分别为二叉搜索树;
2.二叉搜索树非递归模拟实现
#pragma once
#include <cassert>
namespace BinarySearchTree
{template <class K>struct BSTreeNode{BSTreeNode(const K &key = 0) : left_(nullptr), right_(nullptr), key_(key) {}BSTreeNode<K> *left_;BSTreeNode<K> *right_;K key_;};template <class K>class BSTree{// 内嵌类型typedef BSTreeNode<K> node;public:// 默认成员函数BSTree() : root_(nullptr){}~BSTree() {}public:// 普通成员函数bool insert(const K &key);void inorder(){_inorder(root_);}void _inorder(node *root);bool find(const K &key);bool erase(const K &key);private:// 成员变量node *root_;};template <class K>bool BSTree<K>::insert(const K &key){if (root_ == nullptr){root_ = new node(key);return true;}node *cur = root_;node *parent = root_;while (cur){if (cur->key_ == key){return false;}else if (key > cur->key_){parent = cur;cur = cur->right_;}else{parent = cur;cur = cur->left_;}}cur = new node(key);if (key > parent->key_){parent->right_ = cur;}else{parent->left_ = cur;}return true;}template <class K>void BSTree<K>::_inorder(BSTree<K>::node *root){if (root == nullptr){return;}_inorder(root->left_);cout << root->key_ << " ";_inorder(root->right_);}template <class K>bool BSTree<K>::find(const K &key){if (root_ == nullptr){return false;}node *cur = root_;while (cur){if (key == cur->key_){return true;}else if (key > cur->key_){cur = cur->right_;}else{cur = cur->left_;}}return false;}template <class K>bool BSTree<K>::erase(const K &key){node *cur = root_;node *parent = cur;while (cur){if (key == cur->key_){// 找到了,托孤要考虑删root;// 没有孩子,托孤nullptr// 有一个孩子,托孤if (cur->left_ == nullptr){if (cur == root_){parent = cur->right_;}else{if (key_ > parent->key_){parent->right_ = cur->right_;}else{parent->left_ = cur->right_;}}}else if (cur->right_ == nullptr){if (cur == root_){parent = cur->left_;}else{if (key_ > parent->key_){parent->right_ = cur->left_;}else{parent->left_ = cur->left_;}}}else // 有两个孩子,要取左子树最右或者右子树最左{node *leftmax = cur->left_; // 可能cur->left为leftmaxnode *pleftmax = cur;while (leftmax->right_){pleftmax = leftmax;leftmax = leftmax->right_;}std::swap(cur->key_, leftmax->key_);if (pleftmax->left_ == leftmax){pleftmax->left_ = leftmax->left_;}else{pleftmax->right_ = leftmax->left_;}cur = leftmax;}delete cur;return true;}else if (key > cur->key_){parent = cur;cur = cur->right_;}else{parent = cur;cur = cur->left_;}}return false;}}
3.二叉搜索树优点
1.查找效率高;
2.可以顺便实现排序,升序;
3.插入删除效率都不错;
4.二叉搜索树递归实现
#pragma once
#include <cassert>
namespace BinarySearchTree
{template <class K>struct BSTreeNode{BSTreeNode(const K &key = 0) : left_(nullptr), right_(nullptr), key_(key) {}BSTreeNode<K> *left_;BSTreeNode<K> *right_;K key_;};template <class K>class BSTree{// 内嵌类型typedef BSTreeNode<K> node;public:// 默认成员函数BSTree() : root_(nullptr){}BSTree(const BSTree<K> &t){root_ = copy(t.root_);}BSTree<K> &operator=(BSTree<K> t){swap(*this, t);return *this;}~BSTree(){destroy(root_);}public:// 普通成员函数void swap(BSTree<K> &t);bool insert(const K &key){return _insert(root_, key);}void inorder(){_inorder(root_);cout << endl;}bool find(const K &key){return _find(root_, key);}bool erase(const K &key){return _erase(root_, key);}private:// 私有成员node *copy(node *root);void destroy(node *&root);bool _insert(node *&root, const K &key);bool _find(node *root, const K &key);void _inorder(node *root);bool _erase(node *&root, const K &key);node *root_;};template <class K>bool BSTree<K>::_insert(node *&root, const K &key){if (root == nullptr){root = new node(key);return true;}if (key > root->key_){return _insert(root->right_, key);}else if (key < root->key_){return _insert(root->left_, key);}else{return false;}}template <class K>void BSTree<K>::_inorder(node *root){if (root == nullptr){cout << "nullptr"<< " ";return;}_inorder(root->left_);cout << root->key_ << " ";_inorder(root->right_);}template <class K>bool BSTree<K>::_find(node *root, const K &key){if (root == nullptr){return false;}if (key > root->key_){return _find(root->right_, key);}else if (key < root->key_){return _find(root->left_, key);}else{return true;}}template <class K>bool BSTree<K>::_erase(node *&root, const K &key){if (root == nullptr){return false;}if (key > root->key_){return _erase(root->right_, key);}else if (key < root->key_){return _erase(root->left_, key);}else{node *del = root;if (root->left_ == nullptr){root = root->right_;}else if (root->right_ == nullptr){root = root->left_;}else{node *leftmax = root->left_;while (leftmax->right_){leftmax = leftmax->right_;}std::swap(leftmax->key_, root->key_);return _erase(root->left_, key);}delete del;return true;}}template <class K>void BSTree<K>::destroy(node *&root){if (root == nullptr){return;}destroy(root->left_);destroy(root->right_);delete root;root = nullptr;}template <class K>typename BSTree<K>::node *BSTree<K>::copy(node *root){if (root == nullptr){return nullptr;}node *newnode = new node(root->key_);newnode->left_ = copy(root->left_);newnode->right_ = copy(root->right_);return newnode;}template <class K>void BSTree<K>::swap(BSTree<K> &t){std::swap(root_, t.root_);}
}
5.二叉搜索树的应用场景
5.1key的搜索模型(在不在的场景)
门禁系统、车辆输入系统、查找单词是否拼写错误,将词库放到一颗搜索树之中,然后find。
5.1key/value的搜索模型(通过一个值找另外一个值)
手机号找快递信息、停车场(按时计费)、身份证检票查找车票信息,不用制造车票并往车票里写入信息;
namespace key_value
{template <class K, class V>struct BSTreeNode{BSTreeNode(const K &key = K(), const V &value = V()) : left_(nullptr), right_(nullptr), key_(key), value_(value) {}BSTreeNode<K, V> *left_;BSTreeNode<K, V> *right_;K key_;V value_;};template <class K, class V>class BSTree{// 内嵌类型public:typedef BSTreeNode<K, V> node;public:// 默认成员函数BSTree() : root_(nullptr){}~BSTree(){}public:// 普通成员函数bool insert(const K &key, const V &value){return _insert(root_, key, value);}void inorder(){_inorder(root_);cout << endl;}node *find(const K &key){return _find(root_, key);}bool erase(const K &key){return _erase(root_, key);}private:// 私有成员bool _insert(node *&root, const K &key, const V &value);node *_find(node *root, const K &key);void _inorder(node *root);bool _erase(node *&root, const K &key);node *root_;};template <class K, class V>bool BSTree<K, V>::_insert(node *&root, const K &key, const V &value){if (root == nullptr){root = new node(key, value);return true;}if (key > root->key_){return _insert(root->right_, key, value);}else if (key < root->key_){return _insert(root->left_, key, value);}else{return false;}}template <class K, class V>void BSTree<K, V>::_inorder(node *root){if (root == nullptr){return;}_inorder(root->left_);cout << root->key_ << " : " << root->value_ << " ";_inorder(root->right_);}template <class K, class V>typename BSTree<K, V>::node *BSTree<K, V>::_find(node *root, const K &key){if (root == nullptr){return nullptr;}if (key > root->key_){return _find(root->right_, key);}else if (key < root->key_){return _find(root->left_, key);}else{return root;}}template <class K, class V>bool BSTree<K, V>::_erase(node *&root, const K &key){if (root == nullptr){return false;}if (key > root->key_){return _erase(root->right_, key);}else if (key < root->key_){return _erase(root->left_, key);}else{node *del = root;if (root->left_ == nullptr){root = root->right_;}else if (root->right_ == nullptr){root = root->left_;}else{node *leftmax = root->left_;while (leftmax->right_){leftmax = leftmax->right_;}std::swap(leftmax->key_, root->key_);return _erase(root->left_, key);}delete del;return true;}}
}
相关文章:

c++二叉树
二叉树进阶 1.二叉搜索树(binary search tree) 二叉搜索树天然就适合查找,对于满二叉树或者完全二叉树,最多搜索lgn次(就像是有序数组二分查找,每次搜索都会减少范围),极端情况简化成单链表就要走n次,即要走高度次…...

第19章-IPv6基础
1. IPv4的缺陷 2. IPv6的优势 3. 地址格式 3.1 格式 3.2 长度 4. 地址书写压缩 4.1 段内前导0压缩 4.2 全0段压缩 4.3 例子1 4.4 例子 5. 网段划分 5.1 前缀 5.2 接口标识符 5.3 前缀长度 5.4 地址规模分类 6. 地址分类 6.1 单播地址 6.2 组播地址 6.3 任播地址 6.4 例子 …...
浅谈人才招聘APP开发的解决方案
随着企业竞争加剧,高效、精准地招聘人才成为企业持续发展的关键。人才招聘系统能够简化招聘流程,提高效率,确保企业快速找到合适人才。同时,通过智能匹配和数据分析,提升招聘质量,优化候选人体验。因此&…...
)
大语言模型LLM推理加速:Hugging Face Transformers优化LLM推理技术(LLM系列12)
文章目录 大语言模型LLM推理加速:Hugging Face Transformers优化LLM推理技术(LLM系列12)引言Hugging Face Transformers库的推理优化基础模型级别的推理加速策略高级推理技术探索硬件加速与基础设施适配案例研究与性能提升效果展示结论与未来展望大语言模型LLM推理加速:Hug…...

JVM 第四部分—垃圾回收相关概念 2
System.gc() 在默认情况下,通过System.gc()或者Runtime.getRuntime().gc()的调用,会显式触发Full GC,同时对老年代和新生代进行回收,尝试释放被丢弃对象占用的内存 然而System.gc()调用附带一个免责声明,无法保证对垃…...

tritonserver学习之八:redis_caches实践
tritonserver学习之一:triton使用流程 tritonserver学习之二:tritonserver编译 tritonserver学习之三:tritonserver运行流程 tritonserver学习之四:命令行解析 tritonserver学习之五:backend实现机制 tritonserv…...
2024有哪些免费的mac苹果电脑深度清理工具?CleanMyMac X
苹果电脑用户们,你们是否经常感到你们的Mac变得不再像刚拆封时那样迅速、流畅?可能是时候对你的苹果电脑进行一次深度清理了。在这个时刻,拥有一些高效的深度清理工具就显得尤为重要。今天,我将介绍几款优秀的苹果电脑深度清理工具…...

UE5中实现后处理深度描边
后处理深度描边可以通过取得边缘深度变化大的区域进行描边,一方面可以用来做角色的等距内描边,避免了菲尼尔边缘光不整齐的问题,另一方面可以结合场景扫描等特效使用,达到更丰富的效果: 后来解决了开启TAA十字线和锯齿…...

Java面试值之集合
集合 1.HashMap底层?扩容机制?1.7-1.8的升级?2.HashMap的长度为什么是2的幂次方?3.HashMap 插入1.7和1.8的区别?4.什么是红黑树?O(logn)5.HashMap为什么会使用红黑树?6.ArrayList底层?扩容机制?7.LinkedList底层?扩容机制?8.ArrayList可以序列化,但是为什么不直接序…...

React之组件定义和事件处理
一、组件的分类 在react中,组件分为函数组件和class组件,也就是无状态组件和有状态组件。 * 更过时候我们应该区别使用无状态组件,因为如果有状态组件会触发生命周期所对应的一些函数 * 一旦触发他生命周期的函数,它就会影响当前项…...

LeetCode -55 跳跃游戏
LeetCode -55 跳跃游戏 给你一个非负整数数组 nums ,你最初位于数组的 第一个下标 。数组中的每个元素代表你在该位置可以跳跃的最大长度。 判断你是否能够到达最后一个下标,如果可以,返回 true ;否则,返回 false 。…...
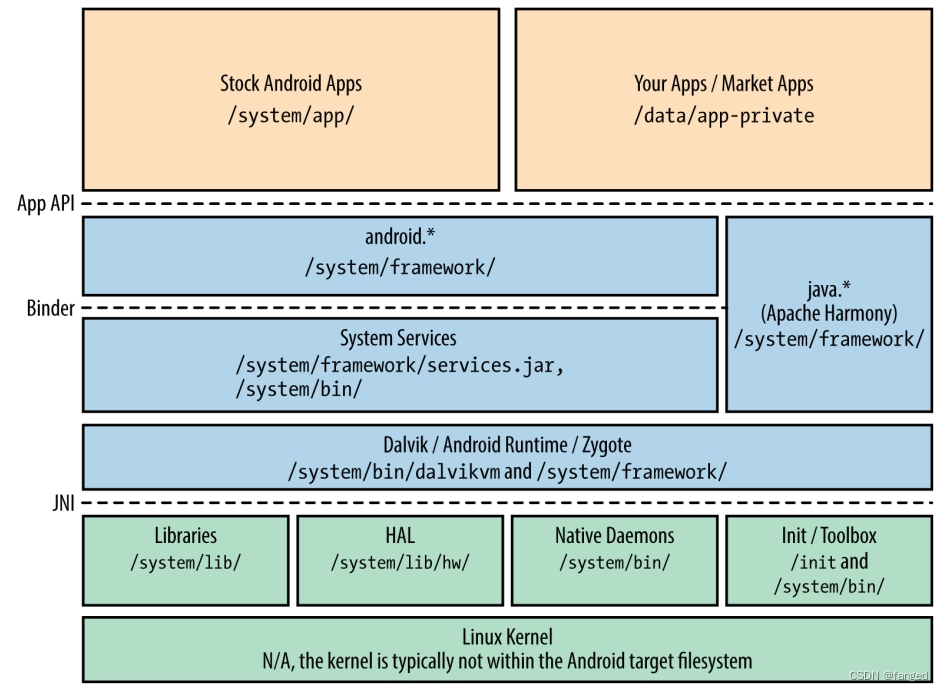
Android和Linux的嵌入式开发差异
最近开始投入Android的怀抱。说来惭愧,08年就听说这东西,当时也有同事投入去看,因为恶心Java,始终对这玩意无感,没想到现在不会这个嵌入式都快要没法搞了。为了不中年失业,所以只能回过头又来学。 首先还是…...

关于Node.js异常处理的教程
在Node.js开发中,异常处理是非常重要的一部分。良好的异常处理可以帮助我们及时发现和解决问题,提高系统的稳定性和可靠性。本教程将向您介绍Node.js中异常处理的最佳实践和策略。 1. 使用try-catch捕获同步异常 在Node.js中,可以使用try-c…...

13. Springboot集成Protobuf
目录 1、前言 2、Protobuf简介 2.1、核心思想 2.2、Protobuf是如何工作的? 2.3、如何使用 Protoc 生成代码? 3、Springboot集成 3.1、引入依赖 3.2、定义Proto文件 3.3、Protobuf生成Java代码 3.4、配置Protobuf的序列化和反序列化 3.5、定义…...

Spring: Springboot 框架集成不同版本的spring redis
文章目录 一、集成不同版本的spring redis1、Spring Data Redis 1.x:2、Spring Data Redis 2.x:3、Spring Data Redis 3.x(Spring Boot 2.x): 二、springboot集成Spring Data Redis 2.x1、首先,确保在 pom.…...
)
学习JAVA的第八天(基础)
目录 多态 前提 形式 测试类 调用成员的特点 优势 劣势 包 注意事项: final关键字 常量 命名规范: 注意事项: 权限修饰符 分类 代码块 局部代码块 构造代码块 静态代码块 抽象类 抽象类: 定义格式 抽象…...
【硬件相关】IB网/以太网基础介绍及部署实践
文章目录 一、前言1、Infiniband网络1.1、网络类型1.2、网络拓扑1.3、硬件设备1.3.1、网卡1.3.2、连接线缆a、光模块b、线缆 1.3.4、交换机 2、Ethernet网络 二、部署实践(以太网)1、Intel E810-XXVDA21.1、网卡信息1.2、检查命令1.2、驱动编译 2、Mella…...
【JavaEE】_Spring MVC项目之建立连接
目录 1. Spring MVC程序编写流程 2. 建立连接 2.1 RequestMapping注解介绍 2.2 RequestMapping注解使用 2.2.1 仅修饰方法 2.2.2 修饰类与方法 2.3 关于POST请求与GET请求 2.3.1 GET请求 2.3.2 POST请求 2.3.3 限制请求方法 1. Spring MVC程序编写流程 1. 建立连接&…...

【JavaEE进阶】 Spring AOP源码简单剖析
文章目录 🍃前言🍀Spring AOP源码剖析⭕总结 🍃前言 前面的博客中,博主对代理模式进行了一个简单的讲解,接下来博主将对Spring AOP源码进行简单剖析,使我们对Spring AOP了解的更加深刻。 🍀Sp…...

Redis--内存回收机制详解
什么是内存回收机制? 众所周知Redis之所以性能高是因为数据都存在内存中,内存是很宝贵的,Redis的内存回收机制本质就是处理达到过期时间的key-value,以及当内存到达最大使用值时候触发的内存淘汰策略。 Redis数据删除的策略有哪些…...

测试微信模版消息推送
进入“开发接口管理”--“公众平台测试账号”,无需申请公众账号、可在测试账号中体验并测试微信公众平台所有高级接口。 获取access_token: 自定义模版消息: 关注测试号:扫二维码关注测试号。 发送模版消息: import requests da…...

conda相比python好处
Conda 作为 Python 的环境和包管理工具,相比原生 Python 生态(如 pip 虚拟环境)有许多独特优势,尤其在多项目管理、依赖处理和跨平台兼容性等方面表现更优。以下是 Conda 的核心好处: 一、一站式环境管理:…...

LeetCode - 394. 字符串解码
题目 394. 字符串解码 - 力扣(LeetCode) 思路 使用两个栈:一个存储重复次数,一个存储字符串 遍历输入字符串: 数字处理:遇到数字时,累积计算重复次数左括号处理:保存当前状态&a…...

微信小程序 - 手机震动
一、界面 <button type"primary" bindtap"shortVibrate">短震动</button> <button type"primary" bindtap"longVibrate">长震动</button> 二、js逻辑代码 注:文档 https://developers.weixin.qq…...

【Oracle】分区表
个人主页:Guiat 归属专栏:Oracle 文章目录 1. 分区表基础概述1.1 分区表的概念与优势1.2 分区类型概览1.3 分区表的工作原理 2. 范围分区 (RANGE Partitioning)2.1 基础范围分区2.1.1 按日期范围分区2.1.2 按数值范围分区 2.2 间隔分区 (INTERVAL Partit…...

Web 架构之 CDN 加速原理与落地实践
文章目录 一、思维导图二、正文内容(一)CDN 基础概念1. 定义2. 组成部分 (二)CDN 加速原理1. 请求路由2. 内容缓存3. 内容更新 (三)CDN 落地实践1. 选择 CDN 服务商2. 配置 CDN3. 集成到 Web 架构 …...

深度学习习题2
1.如果增加神经网络的宽度,精确度会增加到一个特定阈值后,便开始降低。造成这一现象的可能原因是什么? A、即使增加卷积核的数量,只有少部分的核会被用作预测 B、当卷积核数量增加时,神经网络的预测能力会降低 C、当卷…...

Java求职者面试指南:Spring、Spring Boot、Spring MVC与MyBatis技术解析
Java求职者面试指南:Spring、Spring Boot、Spring MVC与MyBatis技术解析 一、第一轮基础概念问题 1. Spring框架的核心容器是什么?它的作用是什么? Spring框架的核心容器是IoC(控制反转)容器。它的主要作用是管理对…...

自然语言处理——文本分类
文本分类 传统机器学习方法文本表示向量空间模型 特征选择文档频率互信息信息增益(IG) 分类器设计贝叶斯理论:线性判别函数 文本分类性能评估P-R曲线ROC曲线 将文本文档或句子分类为预定义的类或类别, 有单标签多类别文本分类和多…...

WEB3全栈开发——面试专业技能点P7前端与链上集成
一、Next.js技术栈 ✅ 概念介绍 Next.js 是一个基于 React 的 服务端渲染(SSR)与静态网站生成(SSG) 框架,由 Vercel 开发。它简化了构建生产级 React 应用的过程,并内置了很多特性: ✅ 文件系…...
