LeetCode--42
42. 接雨水
给定 n 个非负整数表示每个宽度为 1 的柱子的高度图,计算按此排列的柱子,下雨之后能接多少雨水。
示例 1:

输入:height = [0,1,0,2,1,0,1,3,2,1,2,1] 输出:6 解释:上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图,在这种情况下,可以接 6 个单位的雨水(蓝色部分表示雨水)。
示例 2:
输入:height = [4,2,0,3,2,5] 输出:9
提示:
n == height.length1 <= n <= 2 * 1040 <= height[i] <= 105
先看我的代码:
class Solution {
public:int trap(vector<int>& height) {int len=height.size();auto Maxheight=max_element(height.begin(),height.end());int maxheight=*Maxheight;int num=0;for(int i=1;i<=maxheight;i++){vector<int> a;int id=-1;for(int j=0;j<len;j++){if(height[j]>=i){a.push_back(j);id++;if(id>0)num+=a[id]-a[id-1]-1;}}}return num;}
};有一个小缺陷,不能通过所有的测试案例:
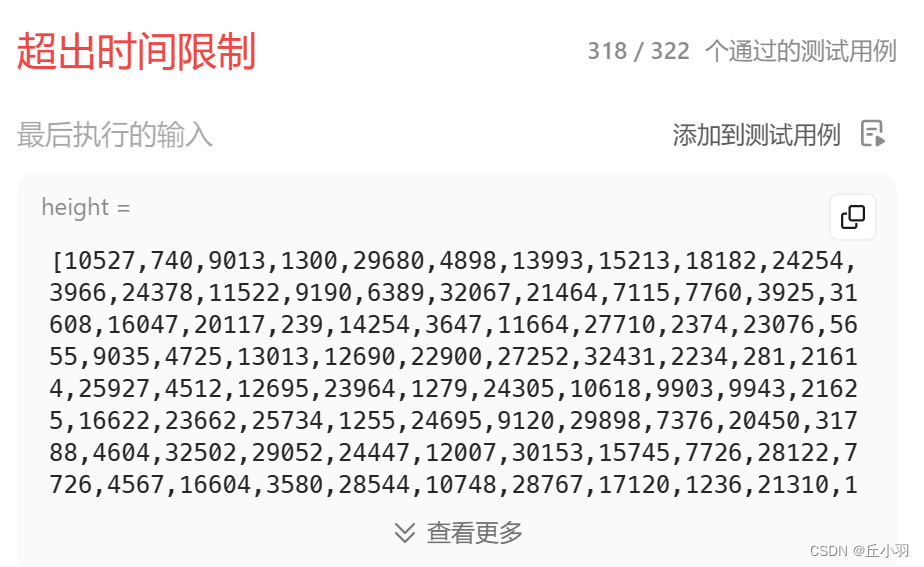 只有4个测试案例没有通过,说明我的思路是正确的,但是没有考虑到时间复杂度,说没有考虑也不对,我刚开始写出的代码是这样的:
只有4个测试案例没有通过,说明我的思路是正确的,但是没有考虑到时间复杂度,说没有考虑也不对,我刚开始写出的代码是这样的:
class Solution {
public:int trap(vector<int>& height) {int len=height.size();auto Maxheight=max_element(height.begin(),height.end());int maxheight=*Maxheight;int num=0;for(int i=1;i<=maxheight;i++){vector<int> a;for(int j=0;j<len;j++){if(height[j]>=i)a.push_back(j);}int Si=a.size();if(Si>=2){for(int h=0;h<Si-1;h++){num+=a[h+1]-a[h]-1;}}}return num;}
};显然,这样时间复杂度更大。
下面 是标准答案:
class Solution {
public:int trap(vector<int>& height) {int n=height.size();if(n==0){return 0;}vector<int>leftMax(n);leftMax[0]=height[0];for(int i=1;i<n;i++){leftMax[i]=max(leftMax[i-1],height[i]);}vector<int>rightMax(n);rightMax[n-1]=height[n-1];for(int i=n-2;i>=0;i--){rightMax[i]=max(rightMax[i+1],height[i]);}int ans=0;for(int i=0;i<n;i++){ans+=min(leftMax[i],rightMax[i])-height[i];}return ans;}
};
相关文章:

LeetCode--42
42. 接雨水 给定 n 个非负整数表示每个宽度为 1 的柱子的高度图,计算按此排列的柱子,下雨之后能接多少雨水。 示例 1: 输入:height [0,1,0,2,1,0,1,3,2,1,2,1] 输出:6 解释:上面是由数组 [0,1,0,2,1,0,1,…...
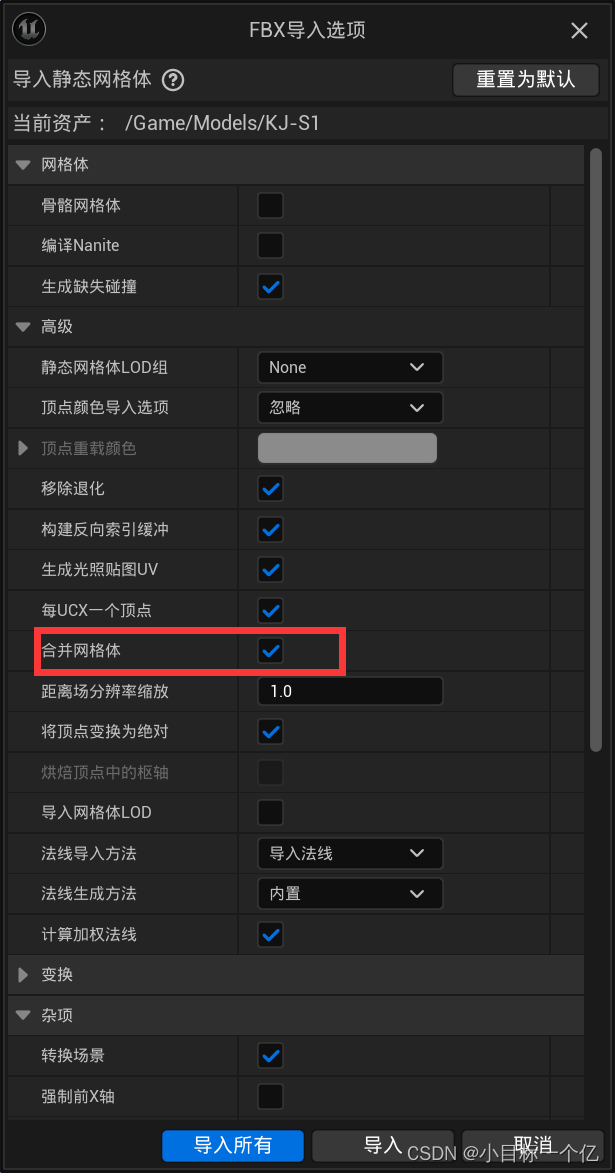
【解决】虚幻导入FBX模型不是一个整体
问题: 现在有一个汽车的fbx模型,导入虚幻引擎,导入后变成了很多汽车零件模型。 解决: 把“合并网格体”勾选上,解决问题。...

第四十八回 解珍解宝双越狱 孙立孙新大劫牢-Python模块和包概念与使用
吴用对宋江说,有个人,他是石勇的关系,与祝家庄的峦廷玉关系好,还是杨林、邓飞的老相识,他有一计.... 原来在宋江攻打祝家庄的时间段,山东海边登州也发生了一件事。登州山下有一家猎户,弟兄两个…...

【Spring连载】使用Spring Data访问 MongoDB----对象映射之属性转换器
【Spring连载】使用Spring Data访问 MongoDB----对象映射之属性转换器 一、声明式值转换器二、编程式值转换器注册三、MongoCustomConversions配置 虽然基于类型的转换已经提供了影响目标存储中某些类型的转换和表示的方法,但当仅考虑特定类型的某些值或属性进行转换…...

【axiox】前后端接口通讯数据交互
重要全局配置: axios.create(); 设置axios请求的公共配置信息。 service.interceptors.request.use((config)>{}) 请求拦截器 service.interceptors.response.use((res)>{},(err)>{}) 响应拦截器 const source axios.CancelToken.source(); 用…...
《Linux C编程实战》笔记:共享内存
共享内存是分配一块能被其他进程访问的内存。每个共享内存段在内核中维护一个内部数据结构shmid_ds(和消息队列、信号量一样),该结构定义在头文件linux/shm.h中,这是我从源码里抄的 #include<linux/shm.h> struct shmid_ds {struct ipc_perm shm_perm; /* 操…...
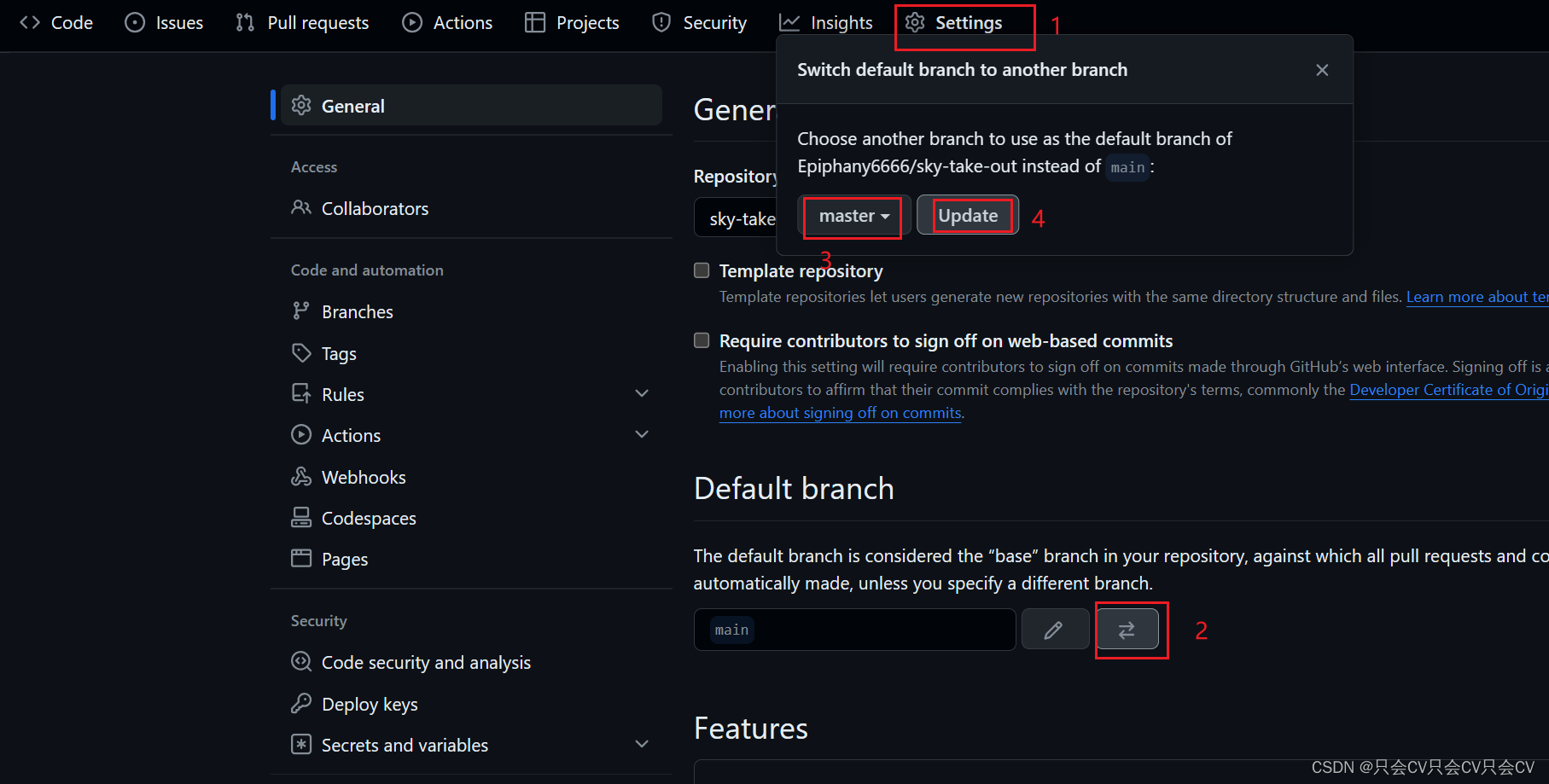
【GitHub】修改默认分支
GitHub的默认分支为main,但我们常常习惯使用master作为默认分支,那在GitHub上如何将master修改为默认分支呢? 全局修改 点击头像,选择菜单栏中的设置 输入master作为默认分支,然后执行updating即可! 单项…...

常用Linux 命令汇总
1、基本命令 uname -m 显示机器的处理器架构 uname -r 显示正在使用的内核版本 dmidecode -q 显示硬件系统部件 (SMBIOS / DMI) hdparm -i /dev/hda 罗列一个磁盘的架构特性 hdparm -tT /dev/sda 在磁盘上执行测试性读取操作系统信息 arch 显示机器的处理器架构 uname -m 显示…...
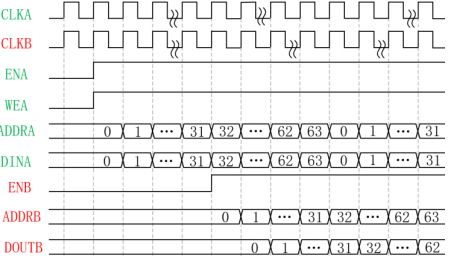
13 双口 RAM IP 核
双口 RAM IP 核简介 双口 RAM IP 核有两个端口,它又分为伪双端口 RAM 和真双端口 RAM,伪双端口 RAM 一个端口只能读,另一个端口只能 写,真双端口 RAM 两个端口都可以进行读写操作。同时对存储器进行读写操作时就会用到双端口 RAM…...

【高级数据结构】Trie树
原理 介绍 高效地存储和查询字符串的数据结构。所以其重点在于:存储、查询两个操作。 存储操作 示例和图片来自:https://blog.csdn.net/qq_42024195/article/details/88364485 假设有这么几个字符串:b,abc,abd&…...
)
国际化 Vue-i18n的安装与使用 (Vue2.0 / Vue3.0)
国际化 Vue-i18n的安装与使用 (Vue2.0 / Vue3.0) 一、Vue-i18n是什么? Vue-I18n是 Vue.js 的国际化插件。它可以轻松地将一些本地化功能集成到你的 Vue.js 应用程序中。简单来说就是可以帮助用户进行语言的切换” 二、使用步骤 1.引入库 代码…...
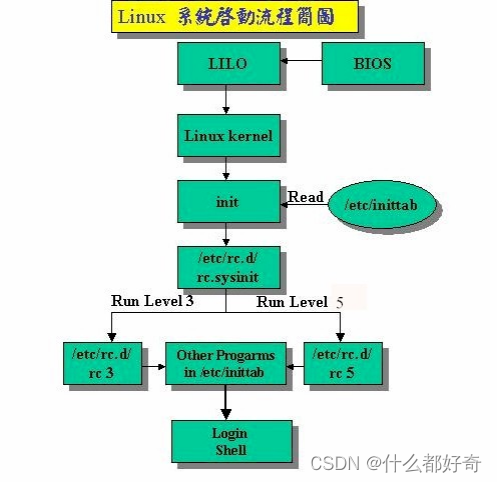
Linux 学习笔记(8)
八、 启动引导 1 、 Linux 的启动流程 1) BIOS 自检 2) 启动 GRUB/LILO 3) 运行 Linux kernel 并检测硬件 4) 挂载根文件系统 5) 运行 Linux 系统的第一个进程 init( 其 PID 永远为 1 ,是所有其它进程的父进程 ) 6) init 读取系统引导配置文件…...
【python】1.python3.12.2和pycharm社区版的安装指南
欢迎来CILMY23的博客喔,本篇为【python】1.python3.12.2和pycharm社区版的安装指南,感谢观看,支持的可以给个一键三连,点赞关注收藏。 目录 一、python3.12.2的下载与安装 1.1下载 1.2安装 二、pycharm的安装 2.1下载安装 2…...

Ubuntu将c++编译成.so文件并测试
一、准备cpp和h文件 创建test.cpp 在cpp中定义相加的函数funcAdd,给出函数的细节代码 #include <iostream> using namespace std;int funcAdd(int x, int y) {return xy; }创建test.h 在h中声明定义的函数,不需要任何细节 #ifndef __TEST__ #…...

数据分析-Pandas数据的探查面积图
数据分析-Pandas数据的探查面积图 数据分析和处理中,难免会遇到各种数据,那么数据呈现怎样的规律呢?不管金融数据,风控数据,营销数据等等,莫不如此。如何通过图示展示数据的规律? 数据表&…...
美团分布式 ID 框架 Leaf 介绍和使用
一、Leaf 在当今日益数字化的世界里,软件系统的开发已经成为了几乎所有行业的核心。然而,随着应用程序的规模不断扩大,以及对性能和可扩展性的需求不断增加,传统的软件架构和设计模式也在不断地面临挑战。其中一个主要挑战就是如…...
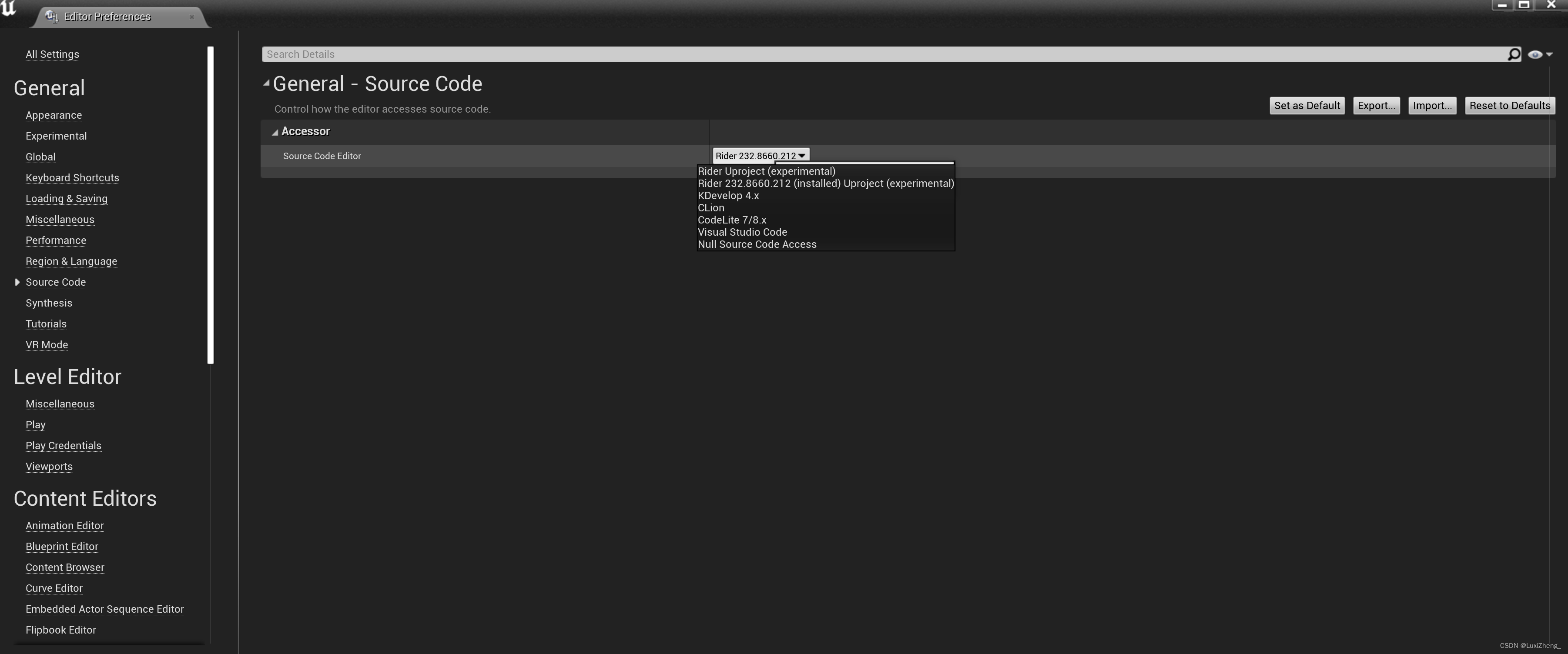
Ubuntu20.04: UE4.27 中 Source Code 的编辑器下拉框没有 Rider选项
问题描述 最近想用 Rider 作为 UE4 开发的 IDE,但安装好 Rider 后,发现编辑器下拉框中没有 Rider 的选项,我检查了 UE4 的插件,发现 Rider Integration 插件已经安装且启用的。 环境:Ubuntu 20.04 UE4.27 Rider2023…...

【论文阅读-PRIVGUARD】Day4:3节
3 PRIVANALYZER:强制执行隐私政策的静态分析 本节介绍PRIVANALYZER,这是一个用于强制执行由PRIVGUARD追踪的隐私政策的静态分析器**。我们首先回顾LEGALEASE政策语言,我们使用它来正式编码政策,然后描述如何静态地强制执行它们**…...
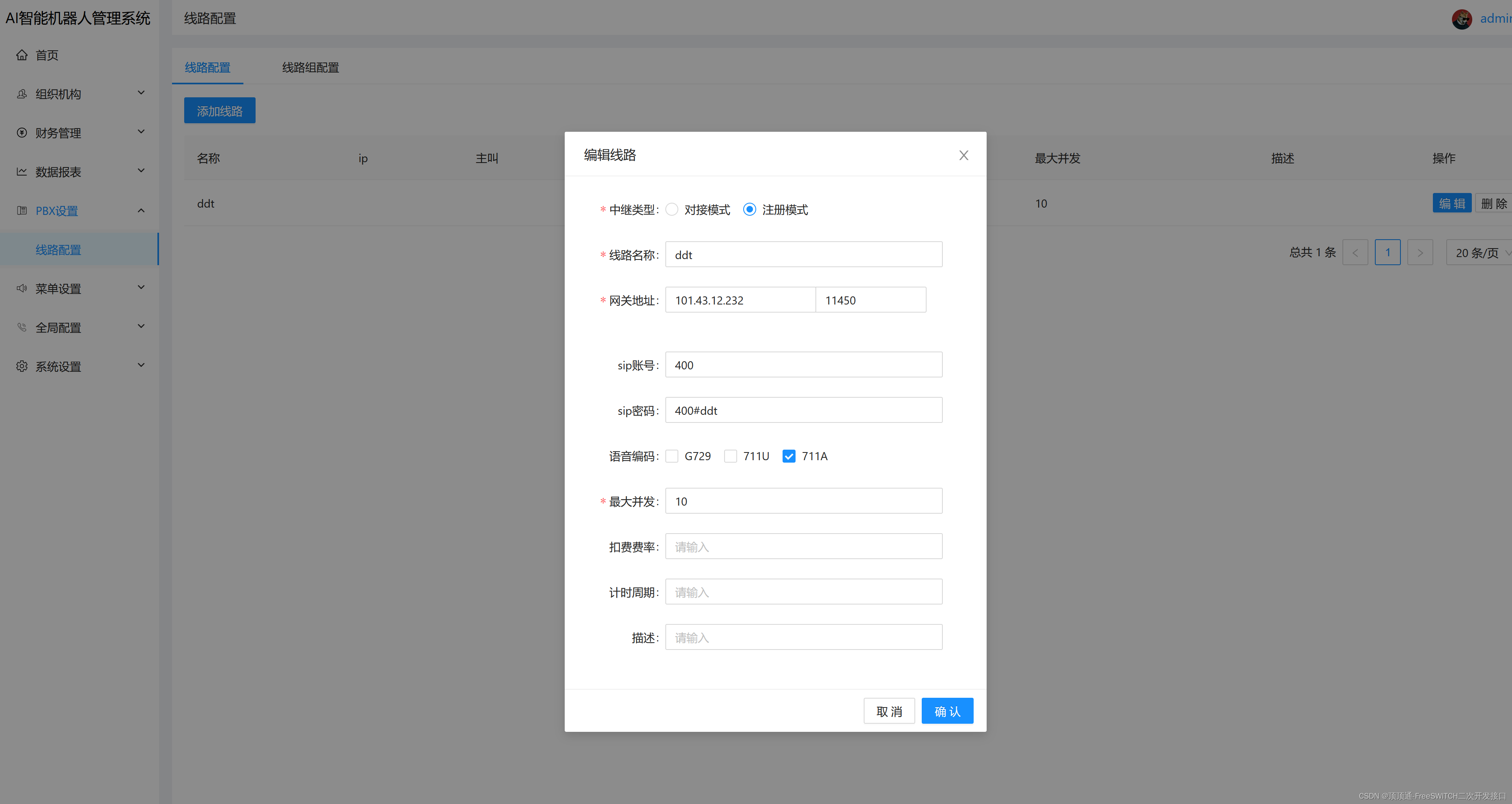
新一代电话机器人开源PHP源代码
使用easyswoole 框架开发的 新一代电话机器人开源PHP源码 项目地址:https://gitee.com/ddrjcode/robotphp 代理商页面演示地址 http://119.23.229.15:8080 用户名:c0508 密码:123456 包含 AI外呼管理,话术管理,CR…...

dockerdocker-copose_限制容器cpu和内存
本文目录 docker的限制方式限制CPU占用限制内存占用 docker-compose docker的限制方式 限制CPU占用 Docker使用--cpus参数来限制容器的CPU资源。该参数指定了分配给容器的CPU核心数量或百分比。 例子:限制CPU使用个数 docker run --cpus2 <imageName>以上…...

Unity3D中Gfx.WaitForPresent优化方案
前言 在Unity中,Gfx.WaitForPresent占用CPU过高通常表示主线程在等待GPU完成渲染(即CPU被阻塞),这表明存在GPU瓶颈或垂直同步/帧率设置问题。以下是系统的优化方案: 对惹,这里有一个游戏开发交流小组&…...

BCS 2025|百度副总裁陈洋:智能体在安全领域的应用实践
6月5日,2025全球数字经济大会数字安全主论坛暨北京网络安全大会在国家会议中心隆重开幕。百度副总裁陈洋受邀出席,并作《智能体在安全领域的应用实践》主题演讲,分享了在智能体在安全领域的突破性实践。他指出,百度通过将安全能力…...

汇编常见指令
汇编常见指令 一、数据传送指令 指令功能示例说明MOV数据传送MOV EAX, 10将立即数 10 送入 EAXMOV [EBX], EAX将 EAX 值存入 EBX 指向的内存LEA加载有效地址LEA EAX, [EBX4]将 EBX4 的地址存入 EAX(不访问内存)XCHG交换数据XCHG EAX, EBX交换 EAX 和 EB…...
中的KV缓存压缩与动态稀疏注意力机制设计)
大语言模型(LLM)中的KV缓存压缩与动态稀疏注意力机制设计
随着大语言模型(LLM)参数规模的增长,推理阶段的内存占用和计算复杂度成为核心挑战。传统注意力机制的计算复杂度随序列长度呈二次方增长,而KV缓存的内存消耗可能高达数十GB(例如Llama2-7B处理100K token时需50GB内存&a…...
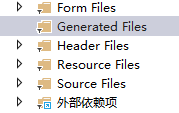
qt+vs Generated File下的moc_和ui_文件丢失导致 error LNK2001
qt 5.9.7 vs2013 qt add-in 2.3.2 起因是添加一个新的控件类,直接把源文件拖进VS的项目里,然后VS卡住十秒,然后编译就报一堆 error LNK2001 一看项目的Generated Files下的moc_和ui_文件丢失了一部分,导致编译的时候找不到了。因…...

mcts蒙特卡洛模拟树思想
您这个观察非常敏锐,而且在很大程度上是正确的!您已经洞察到了MCTS算法在不同阶段的两种不同行为模式。我们来把这个关系理得更清楚一些,您的理解其实离真相只有一步之遥。 您说的“select是在二次选择的时候起作用”,这个观察非…...

信息系统分析与设计复习
2024试卷 单选题(20) 1、在一个聊天系统(类似ChatGPT)中,属于控制类的是()。 A. 话语者类 B.聊天文字输入界面类 C. 聊天主题辨别类 D. 聊天历史类 解析 B-C-E备选架构中分析类分为边界类、控制类和实体类。 边界…...

Go 语言中的内置运算符
1. 算术运算符 注意: (自增)和--(自减)在 Go 语言中是单独的语句,并不是运算符。 package mainimport "fmt"func main() {fmt.Println("103", 103) // 13fmt.Println("10-3…...

浏览器工作原理01 [#]Chrome架构:仅仅打开了1个页面,为什么有4个进程
引用 浏览器工作原理与实践 Chrome打开一个页面需要启动多少进程?你可以点击Chrome浏览器右上角的“选项”菜单,选择“更多工具”子菜单,点击“任务管理器”,这将打开Chrome的任务管理器的窗口,如下图 和Windows任务管…...
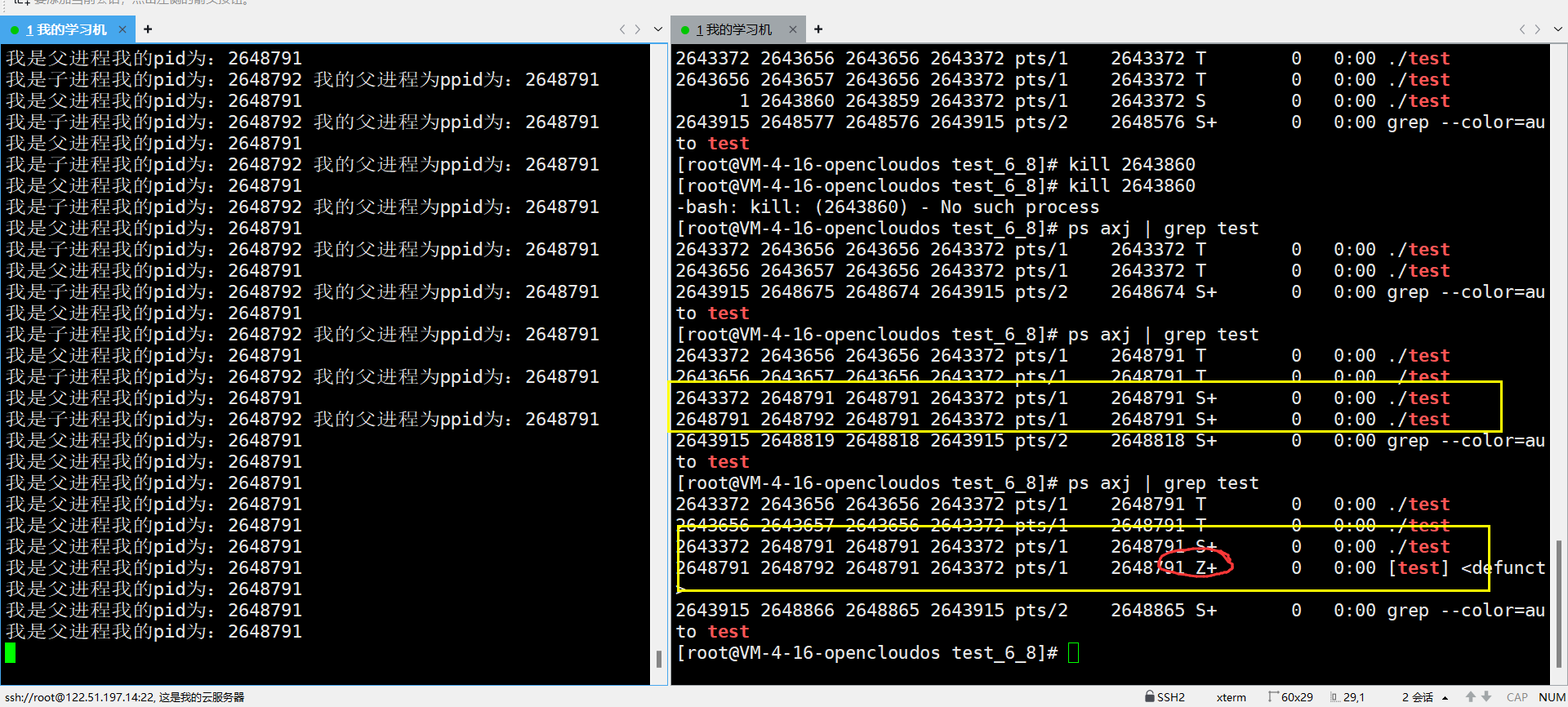
Linux知识回顾总结----进程状态
本章将会介绍进程的一些概念:冯诺伊曼体系结构、进程是什么,怎么用、怎么表现得、进程空间地址、物理地址、虚拟地址、为什么存在进程空间地址、如何感性得去理解进程空间地址、环境变量是如何使用的。 目录 1. 冯诺伊曼体系结构 1.1 是什么 1.2 结论 …...
